Pareto-Based Candidate Selection

• Pareto-based candidate selection is a framework that uses Pareto optimality to evaluate and rank candidates across conflicting objectives.
• It incorporates methods like hypervolume subset selection and preference aggregation to efficiently navigate high-dimensional, stochastic search spaces.
• The approach underpins diverse applications ranging from AI model selection and privacy-preserving data analysis to evolutionary optimization and political candidate formulation.

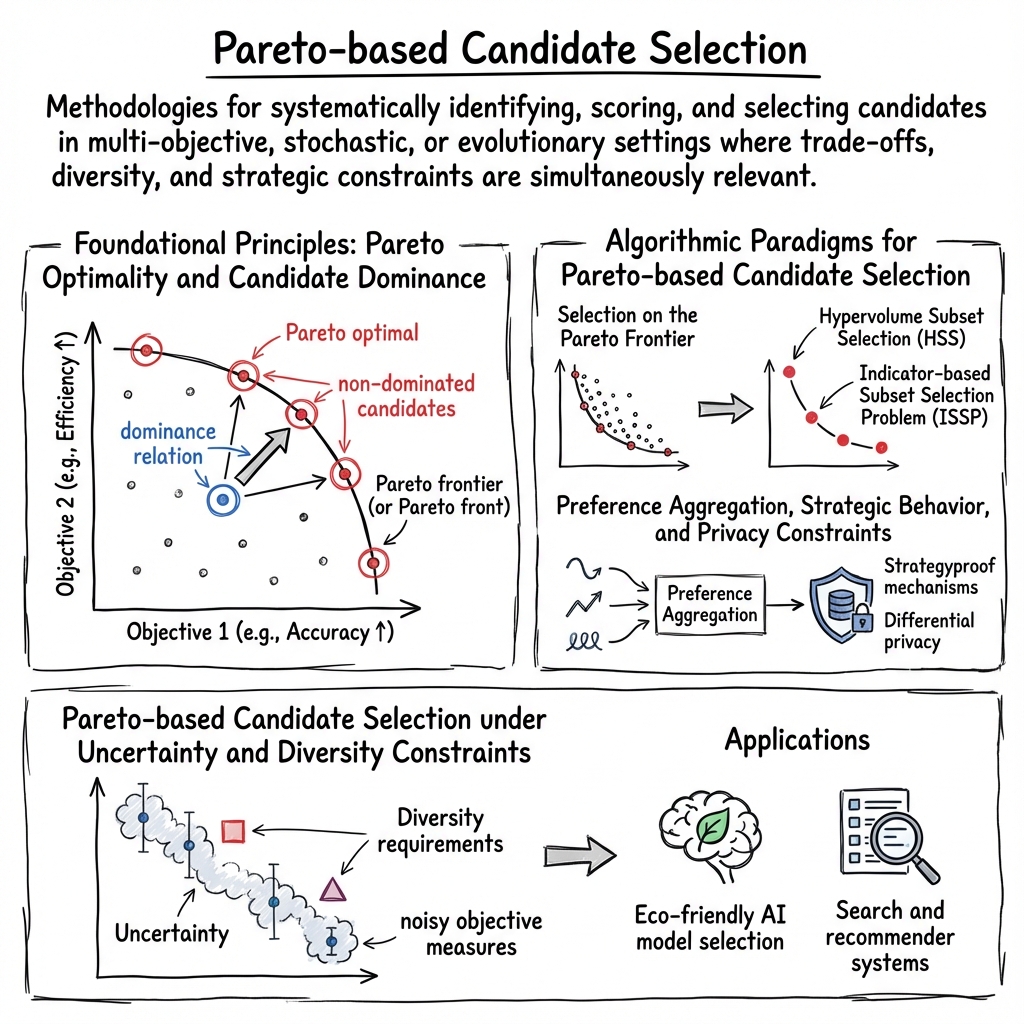
Pareto-based candidate selection encompasses a range of methodologies for systematically identifying, scoring, and selecting candidates (solutions, profiles, committee members, etc.) in multi-objective, stochastic, or evolutionary settings where trade-offs, diversity, and strategic constraints are simultaneously relevant. The Pareto principle, Pareto dominance, and Pareto optimality provide the mathematical and algorithmic underpinnings for many contemporary approaches to candidate selection, including applications in population genetics, resource allocation, algorithm configuration, committee formation, privacy-preserving data analysis, and adversarial political environments.

1. Foundational Principles: Pareto Optimality and Candidate Dominance

A candidate is said to be Pareto optimal if improving one of its evaluation metrics (objectives, fitness, utility) cannot be done without worsening at least one other. This induces a partial ordering—the dominance relation—on the candidate set, with the Pareto frontier (or Pareto front) comprising all non-dominated candidates. Formally, for objectives $f_1, \ldots, f_m$, candidate $x^*$ is Pareto optimal if and only if there does not exist another candidate $x$ such that $f_i(x) \leq f_i(x^*)$ for all $i$ and $f_j(x) < f_j(x^*)$ for at least one $j$.

In practical contexts, candidate scoring frequently utilizes Pareto-inspired mechanisms, such as:

• Pareto scores: Quantifying the degree to which a candidate is dominated by others, e.g., $PS(x, r) = -|\{ r' \in R : r' \succeq^x r \}|$ (Farias et al., 18 Dec 2024).
• Generalized topological sorting and k-Pareto optimality: Sorting and extracting maximum-choice subsets from candidate sets with respect to the strict dominance relation $R^*$ (Ruppert et al., 2022).
• Constructing normalized partitions (e.g., from Pareto-distributed random variables) and calculating coalescent probabilities for genealogical inference (Huillet, 2013).

Dominance relations and Pareto optimality are thus universal primitives both in algorithm specification and in the theoretical analysis of candidate selection processes.

2. Algorithmic Paradigms for Pareto-based Candidate Selection

2.1 Selection on the Pareto Frontier

The typical use case involves selecting desirable candidates from the Pareto front (or an approximation thereof). Subset selection approaches include:

• Hypervolume Subset Selection (HSS): Extracting a subset of size $k$ that maximizes the hypervolume indicator (Ishibuchi et al., 2020).
• Indicator-based Subset Selection Problem (ISSP): Maximizing a quality indicator (e.g., hypervolume, IGD, R2, NR2) over all $k$-subsets, often via local search accelerated by candidate lists (nearest or random neighbors) to reduce computational cost (Korogi et al., 6 Mar 2025).
• Stochastic interventions in high-dimensional attribute spaces: Learning an optimal probability distribution over candidate profiles subject to expected utility and regularization constraints (Jerzak et al., 26 Apr 2025).

Heuristic and evolutionary algorithms commonly extend to the multiobjective setting with Pareto-based selection pressures, including genetic algorithms using the Pareto principle to pre-filter candidates and optimize solution quality and efficiency (e.g., using only the top 20% per-task candidates (Khatoonabadi et al., 2021)).

2.2 Preference Aggregation, Strategic Behavior, and Privacy Constraints

Pareto optimality in aggregative decision contexts is linked to specific extensions of agent preferences over single alternatives to subsets, such as:

• Responsive, Downward Lexicographic, Upward Lexicographic, Best, and Worst set extensions; each yields a distinct (and often computationally complex) definition of committee Pareto optimality (Aziz et al., 2018).
• Serial dictatorship and strategyproof mechanisms: Achieving optimality and immunity to manipulation in linear time for certain set extensions via iterative, agent-prioritized candidate fixing.

Differential privacy introduces additional constraints, with mechanisms like PrivPareto and PrivAgg identifying candidates “near” the Pareto frontier or aggregating objectives, and computing their global/local sensitivities for privacy-preserving selection (Farias et al., 18 Dec 2024).

3. Pareto-based Candidate Selection under Uncertainty and Diversity Constraints

Realistic candidate selection often involves uncertainty (e.g., noisy objective measures, incomplete information) and diversity requirements.

• Bayesian bi-objective ranking and selection with stochastic kriging: Using predictive metamodels to direct additional sampling where it most reduces the error in Pareto front identification, via criteria like Expected Hypervolume Difference (EHVD) and Posterior Distance (PD) (Gonzalez et al., 2022).
• Diversity-aware conformal selection (DACS): Optimizing the selection set via layered optimization (inner for maximum diversity subject to statistical e-value self-consistency/FDR control, outer for optimal stopping) with flexible diversity metrics, including underrepresentation indices and Markowitz/Sharpe-ratio objectives (Nair et al., 19 Jun 2025).

DACS exemplifies Pareto-based selection as a trade-off between statistical quality constraints (e.g., FDR) and maximal coverage of desired diversity features, leveraging a formal optimization over selections and stopping times.

4. Applications and Domain-specific Instantiations

Pareto-based candidate selection is applied across diverse domains:

• Evolutionary multi-objective optimization: Extraction and subset selection from non-dominated solution sets for practical decision making, often with user-interpreted expected loss or coverage trade-offs (Ishibuchi et al., 2020).
• Eco-friendly AI model selection: Inference-time selection of model/epoch pairs that jointly optimize validation accuracy and energy consumption across multiple AI tasks, using predictor-driven Pareto front extraction and user-weighted final ranking (Betello et al., 2 May 2025).
• Search and recommender systems: Post-hoc model selection from the Pareto front based on deterministic or calibrated population distances from per-instance utopia points (Population Distance from Utopia, PDU), balancing global and individualized objectives (Paparella et al., 2023).
• Political candidate profile optimization: Stochastic intervention strategies in adversarial (game-theoretic) selection environments, deriving equilibrium solutions that robustly maximize expected outcomes under mutual competition (Jerzak et al., 26 Apr 2025).
• Web service composition: Pool pruning and evolutionary optimization, where the Pareto principle drives candidate reduction and final solution quality for composite service construction (Khatoonabadi et al., 2021).
• Differential privacy: Pareto scoring and aggregation methods for multi-objective selection under privacy constraints, illustrated for cost-sensitive decision trees and influence maximization in networks (Farias et al., 18 Dec 2024).

5. Theoretical and Practical Trade-offs

Pareto-based approaches must balance multiple axes:

• Computational Tractability: Exact computation of optimalk-subsets or Pareto fronts is combinatorially hard; practical methods deploy local search with restricted neighborhoods, greedy/incremental subset construction, and evolutionary algorithms with candidate list strategies (Korogi et al., 6 Mar 2025, Ishibuchi et al., 2020).
• Approximation and Performance Metrics: Quality is typically assessed using domain-indicator alignment (e.g., hypervolume, IGD, ranking alignment), with trade-offs between exploration (diversity) and exploitation (quality) managed through problem-specific metrics and user/instance-weighted selection (Betello et al., 2 May 2025).
• Strategic and Privacy Constraints: Serial dictatorship offers strategyproofness in preference aggregation (Aziz et al., 2018), while composition of objective sensitivities ensures privacy preservation in data analysis (Farias et al., 18 Dec 2024). Adversarial setups ensure robustness and equilibrium in multicandidate systems (Jerzak et al., 26 Apr 2025).
• Scalability: Adoption of candidate lists, indicator relaxations, and dynamic programming (for optimal stopping) greatly improves performance in settings with large candidate pools or high-dimensional objective spaces (Korogi et al., 6 Mar 2025, Nair et al., 19 Jun 2025).

6. Mathematical Formulation and Key Expressions

Central mathematical objects include:

Construct	Definition/Formula	Context
Pareto Score	$PS(x, r) = -|\{ r' \in R : r' \succeq^x r \}|$	DP multi-objective selection (Farias et al., 18 Dec 2024)
Expected Loss (subset sel)	$$Loss(A, S) = \frac{1}{|S|}\sum_{s \in S} \min_{a \in A} Loss(a,s)$$	IGD⁺, subset selection (Ishibuchi et al., 2020)
DACS inner program	maximize $\phi(Z_{\mathcal{R}}^{\text{test}})$ s.t. e-value constraints	FDR + diversity (Nair et al., 19 Jun 2025)
Aggregated utility (PrivAgg)	$u_{agg}(x,r) = \sum_{i=1}^m w_i u_i(x,r)$	Differential privacy, multi-obj selection (Farias et al., 18 Dec 2024)
Model selection regret	$$R_T = O( \log^{7/2}(K T \log T) \cdot T^{\min\{\max\{\beta, 1+\alpha-\beta\},1\}} )$$	Pareto-optimal model selection (Zhu et al., 2021)

These mathematical principles undergird practical implementations, such as the generation of Pareto frontiers, diversity-optimized subsets, privacy-aware candidate releases, and robust adversarial strategies.

7. Future Directions and Open Problems

Ongoing and future research will further develop:

• Online and adaptive Pareto-based selection that incorporates new objectives or evolving user criteria (Betello et al., 2 May 2025).
• Integration of advanced diversity metrics and stopping theory into efficient large-scale conformal selection (Nair et al., 19 Jun 2025).
• Scalable algorithms for high-dimensional, many-objective settings (e.g., surrogate measures for hypervolume, batch selection) (Gonzalez et al., 2022).
• Richer equilibrium and calibration mechanisms in adversarial and personalized contexts (Jerzak et al., 26 Apr 2025, Paparella et al., 2023).

A common thread is the interplay between provable guarantees (optimality, FDR, privacy, strategyproofness) and computational tractability in the presence of multi-dimensional, structured, and often conflicting objectives.

---

In sum, Pareto-based candidate selection constitutes a mathematically grounded, algorithmically sophisticated, and practically impactful framework for multi-objective, high-dimensional, and constraint-laden selection problems across theoretical and applied domains.