LeJEPA: Scalable Self-Supervised Learning

Updated 12 November 2025

LeJEPA is a self-supervised learning framework that employs predictive embeddings and isotropic Gaussian regularization to create optimally structured latent representations.
The SIGReg objective uses random projections and 1-D goodness-of-fit tests to align the empirical embedding distribution with a standard Gaussian, minimizing bias and variance.
Engineered for scalability and architectural agnosticism, LeJEPA demonstrates robust performance across diverse datasets and models without relying on heuristic techniques.

LeJEPA denotes two independent, technically unrelated developments that share a common acronym but arise in distinct domains: (1) “LeJEPA: Provable and Scalable Self-Supervised Learning Without the Heuristics” (Balestriero et al., 11 Nov 2025)—a theoretically grounded self-supervised learning objective for neural representations, and (2) the LeJEPA framework in rough path theory ("General Rough integration, Levy Rough paths and a Levy--Kintchine type formula" (Friz et al., 2012))—a pathwise, algebraic approach to stochastic integration against processes with jumps. Both are significant within their respective fields: statistical learning theory and stochastic analysis. The following exposition focuses on LeJEPA in the self-supervised learning (SSL) literature, as developed in (Balestriero et al., 11 Nov 2025), with references to the rough paths context where relevant.

1. Theoretical Principles of LeJEPA in Self-Supervised Learning

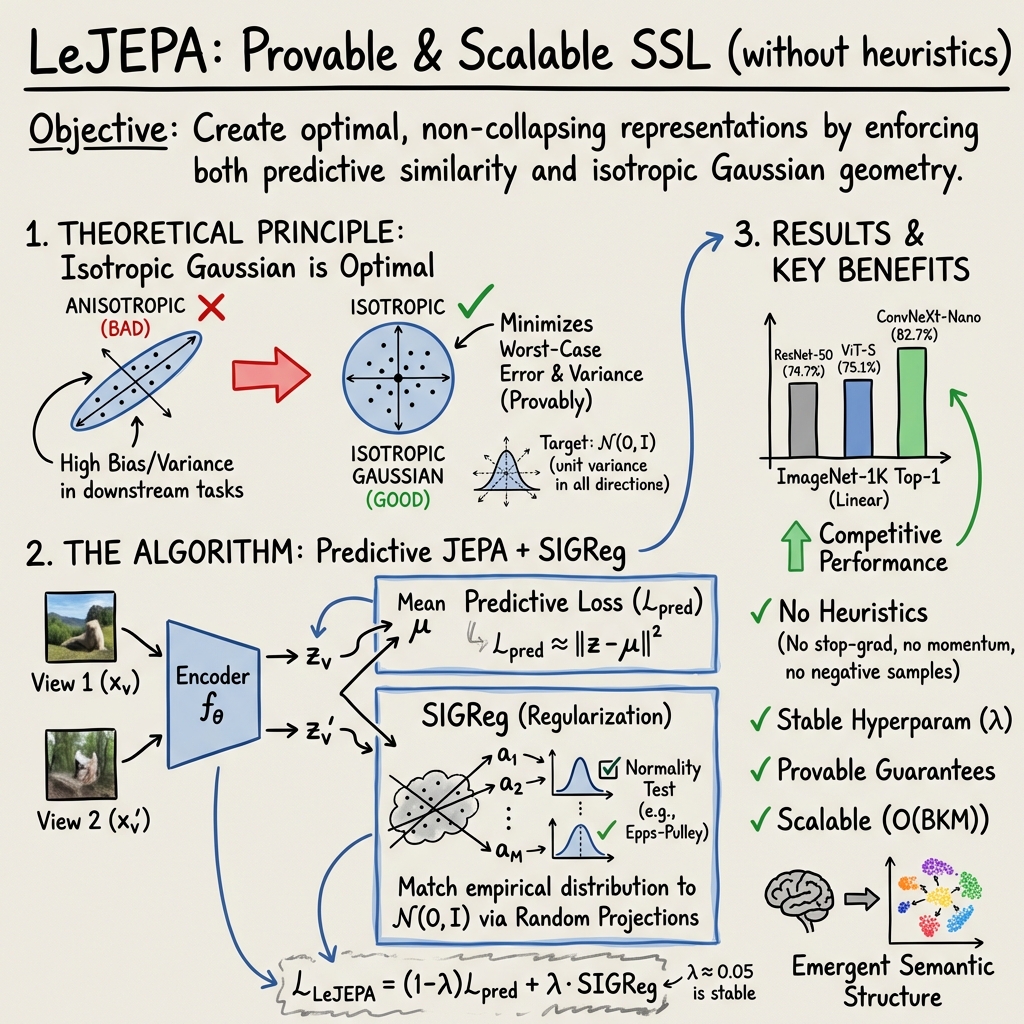
LeJEPA (Balestriero et al., 11 Nov 2025) provides a rigorous mathematical foundation for Joint-Embedding Predictive Architectures (JEPAs), targeting the problem of learning manipulable, transferable representations in a self-supervised regime. A JEPA trains an encoder $f_\theta: \mathbb{R}^D \to \mathbb{R}^K$ such that embeddings of paired, correlated views of data ( $\mathbf{x}_{n,v}$ , $\mathbf{x}_{n,v'}$ ) are predictive of each other, while avoiding representational collapse.

The core insight of LeJEPA is the identification, via rigorous downstream risk minimization, of the isotropic Gaussian distribution as the unique optimal target for the encoder’s latent space. This optimization is justified for both linear (ridge regression) and nonlinear probes (k-NN, kernel regression), as demonstrated by the minimization of worst-case bias and variance under total variance constraints. Explicitly, for the embedding covariance $\Sigma$ , the choice $\Sigma = \frac{\mathrm{tr}(\Sigma)}{K}I$ minimizes both downstream prediction error and variance.

Analytical results (Lemmas 3.1–3.4 and Theorem 3.3 in (Balestriero et al., 11 Nov 2025)) show that any anisotropic embedding distribution inevitably increases bias/variance in downstream tasks. The Fisher information functional $J(p) = \int \|\nabla \log p(\mathbf{z})\|^2p(\mathbf{z})d\mathbf{z}$ quantifies the penalty incurred by deviations from isotropy for nonlinear methods; this is minimized if and only if the embedding distribution is standard Gaussian.

2. The Sketched Isotropic Gaussian Regularization (SIGReg) Objective

To operationalize geometrically optimal embeddings, LeJEPA introduces Sketched Isotropic Gaussian Regularization (SIGReg). SIGReg approaches distribution matching between the empirical embedding distribution $p_z(\mathbf{z})$ and the standard Gaussian $\mathcal{N}(0, I_K)$ . Given a batch of embeddings $\{\mathbf{z}_i\}_{i=1}^N$ , one projects each sample onto $M$ independent random unit vectors $\{\mathbf{a}_m\}$ , yielding scalar projections $\mathbf{a}_m^\top \mathbf{z}_i$ . For each direction, a 1-D goodness-of-fit test statistic $T$ (e.g., Epps–Pulley characteristic function test) is computed, and SIGReg averages this statistic across directions: $\mathrm{SIGReg}_T(\{\mathbf{z}_i\}) = \frac{1}{M}\sum_{m=1}^M T(\{\mathbf{a}_m^\top \mathbf{z}_i\}_{i=1}^N).$ As proven in Theorem 4.5, this random projections methodology is a consistent multivariate normality test in the limit $M \to \infty$ .

The combined LeJEPA loss for training is a convex combination of the predictive JEPA loss ( $\mathcal{L}_{\mathrm{pred}}$ ) and SIGReg: $\mathcal{L}_{\mathrm{LeJEPA}} = (1-\lambda)\,\mathcal{L}_{\mathrm{pred}} + \lambda\,\mathrm{SIGReg}_T(\{\mathbf{z}_i\}),$ where $\lambda \in [0,1]$ controls the trade-off, with empirical results indicating strong stability for $\lambda \approx 0.05$ .

3. Computational Properties and Implementation Details

LeJEPA is engineered for architectural agnosticism, scalability, and distributed training-friendliness. The SIGReg test requires only $\approx 50$ lines of PyTorch and integrates seamlessly with standard backbones—ResNet, ViT, ConvNet, etc. The core steps are:

Forward computation of global view embeddings and their mean $\mu$ .
Per-view prediction loss: squared Euclidean distance between the embedding of each view and $\mu$ .
SIGReg regularization: random projection of embeddings, followed by evaluation of the Epps–Pulley statistic or similar on each direction.
The entire regularization procedure is linear in batch size ( $O(BKM)$ ), with fixed $K, M$ , and DDP (Distributed Data Parallel) compatible.

No stop-gradient, teacher–student momentum encoders, or memory banks are used. Only standard optimizer settings and a single trade-off hyperparameter are needed.

The following pseudocode summarizes the LeJEPA algorithm:

z_g = f(x_global)          # Backbone + projector: [Vg x B x K]
mu = z_g.mean(dim=0)       # [B x K]
z_all = f(x_all)           # [V x B x K]
L_pred = ((z_all - mu) ** 2).mean()
L_reg = (SIGReg(z_all)).mean()    # Over V and batch
L = (1 - lambda) * L_pred + lambda * L_reg
L.backward(); optimizer.step()

Generation of random directions for SIGReg:

1 2	A = torch.randn(K, M) A /= A.norm(dim=0, keepdim=True)

Computation of each Epps–Pulley CF test is performed per projection.

4. Empirical Performance and Robustness

LeJEPA has been validated across 10+ datasets and 60+ architectures spanning vision transformers, convolutional networks, and standard ResNets. Performance metrics in linear evaluation settings on ImageNet-1K (400 epochs, frozen backbone):

Architecture	Top-1 (%)	Full-finetune (%)
ResNet-50	74.7	N/A
ViT-Small/16	75.1	N/A
ConvNeXt-V2-Nano	82.7	82.7
ResNet-34	83.3	83.3
ViT-H/14	79.0	79.0

Average top-1 accuracy on ImageNet-10 (50 diverse models) is 92–95%, with nontrivial performance across all architectures. In-domain pretraining (e.g., Galaxy10) outperforms state-of-the-art alternatives such as DINOv2/v3 and I-JEPA trained on out-of-domain data.

Ablation studies demonstrate:

Stability in $\lambda \in [0.005, 0.1]$ ( $\Delta < 0.5$ %).
Insensitivity to batch sizes from 128 to 1024 (<1% drop).
Robustness to the number of SIGReg slices $M \in [512, 2048]$ and test integration points.

LeJEPA also produces embeddings with emergent semantic structure, such as PCA colorings differentiating object/background and temporally coherent attention for video segmentation.

5. Contrasts with Prior Approaches and Limitations

LeJEPA explicitly removes standard heuristics required for preventing representational collapse found in self-supervised architectures: there is no need for stop-gradient, negative sampling, teacher–student separation, or warmup/burn-in schedules beyond default optimizer settings.

Key strengths:

Provable minimization of bias/variance for all downstream (linear, nonlinear) probes.
No reliance on unstable tricks: single $\lambda$ suffices across tasks, architectures, and domains.
Strong Spearman (>0.9) correlation between validation SSL loss and downstream accuracy, enabling label-free model selection.

Limitations:

SIGReg's effectiveness in very high-dimensional spaces is contingent on sufficient projection coverage ( $M \gtrsim 16$ ), though quasi-Monte Carlo or Sobol sequences improve convergence.
Uses approximate numerical integration in the Epps–Pulley test; however, numerical studies confirm stability.
For embedding distributions with heavy tails (moments >2 unbounded), the characteristic function-based tests may indirectly enforce, but not strictly guarantee, all moment constraints.

6. Extensions and Future Directions

Potential directions for extending LeJEPA include:

Replacement of random projections in SIGReg with low-discrepancy sequences (e.g., Sobol) for tighter normality checks.
Adaptive direction selection, concentrating projection efforts on directions of greatest empirical discrepancy.
Multi-modal extension: applying the same principle to joint representation learning over modalities such as audio and images.
Theoretical characterization of impact on representation spectra, including neural collapse and NTK (Neural Tangent Kernel) asymptotics.

Editor’s note: The acronym LeJEPA is also used for “Levy-Jump-Expected-signature–Pathwise-Analysis” in rough path theory (Friz et al., 2012), where it denotes a deterministic, algebraic, and analytic framework for pathwise stochastic integration and inference with jumps, grounded in the theory of Lévy rough paths, the group-valued Lévy–Khintchine formula, and closed-form expressions for the expected signature. However, there is no technical overlap between the statistical learning and rough paths versions beyond the shared initialism.

7. Conclusion

LeJEPA marks a transition to provable, scalable, and heuristics-free self-supervised learning by uniting rigorous information-theoretic results with a practically efficient implementation paradigm. Its key contribution is the reduction of JEPA training to an objective that enforces both predictive similarity between data views and optimally isotropic, non-degenerate latent distributions. Linear in both computation and memory, LeJEPA beats or matches established baselines while eschewing all special-case collapse-avoidance mechanisms, establishing a robust foundation for future SSL research and practice in both academic and industrial contexts.