LeJEPA: Provable and Scalable Self-Supervised Learning Without the Heuristics (2511.08544v2)
Abstract: Learning manipulable representations of the world and its dynamics is central to AI. Joint-Embedding Predictive Architectures (JEPAs) offer a promising blueprint, but lack of practical guidance and theory has led to ad-hoc R&D. We present a comprehensive theory of JEPAs and instantiate it in {\bf LeJEPA}, a lean, scalable, and theoretically grounded training objective. First, we identify the isotropic Gaussian as the optimal distribution that JEPAs' embeddings should follow to minimize downstream prediction risk. Second, we introduce a novel objective--{\bf Sketched Isotropic Gaussian Regularization} (SIGReg)--to constrain embeddings to reach that ideal distribution. Combining the JEPA predictive loss with SIGReg yields LeJEPA with numerous theoretical and practical benefits: (i) single trade-off hyperparameter, (ii) linear time and memory complexity, (iii) stability across hyper-parameters, architectures (ResNets, ViTs, ConvNets) and domains, (iv) heuristics-free, e.g., no stop-gradient, no teacher-student, no hyper-parameter schedulers, and (v) distributed training-friendly implementation requiring only $\approx$50 lines of code. Our empirical validation covers 10+ datasets, 60+ architectures, all with varying scales and domains. As an example, using imagenet-1k for pretraining and linear evaluation with frozen backbone, LeJEPA reaches 79\% with a ViT-H/14. We hope that the simplicity and theory-friendly ecosystem offered by LeJEPA will reestablish self-supervised pre-training as a core pillar of AI research (\href{https://github.com/rbalestr-lab/lejepa}{GitHub repo}).
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
LeJEPA: A simple explanation for teens
Overview
This paper is about teaching AI systems to learn useful “representations” (smart summaries) of data without any labels, in a way that is both simple and reliable. The authors propose a new method called LeJEPA that gives a clear rule for how these summaries should look and a fast way to make it happen during training. The big idea: make the learned features look like a round, evenly spread cloud of points (an “isotropic Gaussian”). Doing this makes later tasks (like classification) easier and more accurate.
What questions were they trying to answer?
The paper focuses on two main questions:
- How should a good AI model organize its learned features so that simple tools later can solve many different tasks well?
- Can we train models to learn that kind of organized feature space reliably, at large scale, and without lots of fragile tricks?
Their answer is: the features should be shaped like an even, round cloud (not stretched in any direction), and we can train models to do this efficiently using a new regularizer called SIGReg.
How did they do it? Methods explained simply
Before the details, here are a few terms in plain language:
- Representation/Embedding: a compact vector (list of numbers) that summarizes an input (like a picture) so a computer can work with it.
- Views: different versions of the same thing (like different crops or slightly changed colors of the same image).
- JEPA (Joint-Embedding Predictive Architecture): train a model so the embeddings of related views agree or predict each other.
- Collapse: a bad outcome where the model maps everything to almost the same vector, which is useless.
Now, the approach:
1) JEPAs in plain terms
JEPAs train a model by making the embeddings of two related views match or predict each other. For example, two crops of the same photo should produce similar embeddings. This encourages the model to focus on the important meaning (like “dogness”) rather than unimportant details (like exact position).
Problem: JEPAs can “collapse” (learn a shortcut where everything looks the same), so past methods added many tricks (like teacher–student networks, stop-gradient, careful schedules) to avoid that.
2) A clear design rule: make the feature cloud round
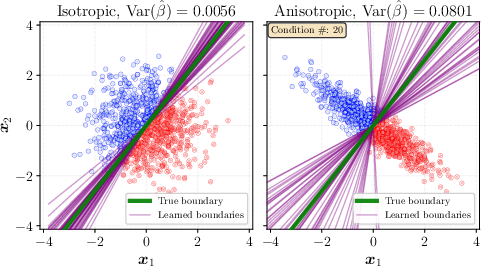
The authors prove something powerful: if you want your features to work well for many future tasks, they should be spread evenly in all directions — like a perfect 3D fog of points with no preferred direction, called an “isotropic Gaussian.”
- Why? If the cloud is stretched or squished (anisotropic), simple tools that read the features later (like a linear probe — think “draw a straight line to separate classes”) become biased or unstable.
- They show this mathematically for both simple “straight-line” readers (linear probes) and more flexible readers (like k-nearest neighbors and kernel methods).
- Intuition: a round cloud is fair to every direction, so it doesn’t accidentally favor or hurt certain tasks.
3) SIGReg: the new, fast rule-enforcer
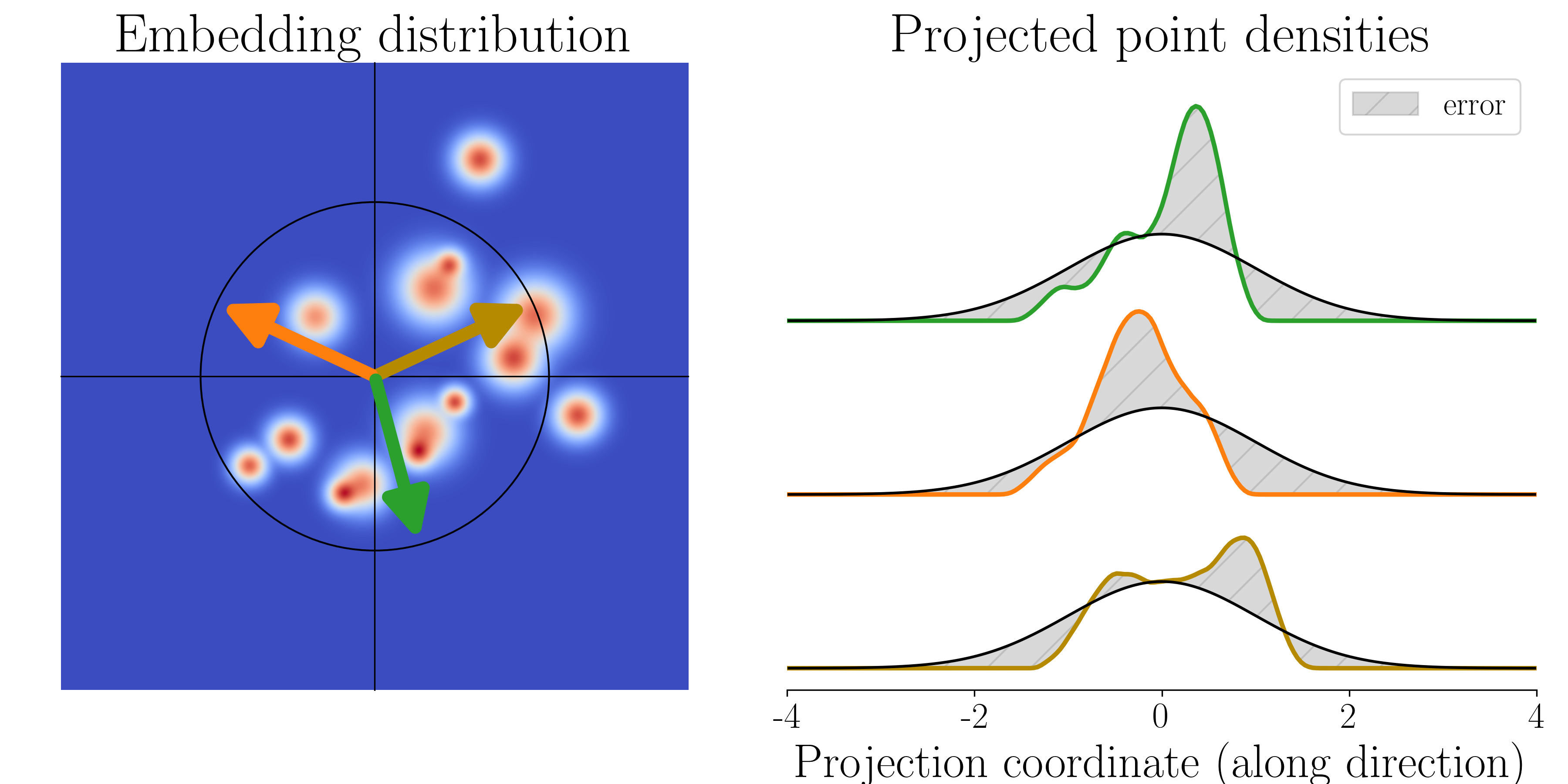
To make the embedding cloud round and Gaussian, they introduce SIGReg (Sketched Isotropic Gaussian Regularization). Here’s the idea:
- Imagine shining a flashlight from many random directions onto the cloud of points and looking at the 1D “shadow” each time.
- If the cloud is truly round and Gaussian, every “shadow” should look like a bell curve.
- SIGReg checks these shadows (using quick math tests) and nudges the model to fix any shadow that doesn’t look bell-shaped.
- This “many shadows” trick avoids the curse of dimensionality: even if the feature vectors are very high-dimensional, checking lots of 1D shadows is still fast and effective.
Technical note in simple words:
- They use a stable test called Epps–Pulley (based on a “characteristic function,” like a frequency fingerprint of a distribution). It’s smooth, has bounded gradients (so training doesn’t explode), needs no sorting, and runs fast on many GPUs.
4) LeJEPA: put it together
LeJEPA = the usual JEPA prediction objective + SIGReg.
- One trade-off knob to balance “predict views” and “make it round Gaussian.”
- No fragile heuristics: no stop-gradient, no teacher–student, no fancy schedules.
- Scales well: linear time and memory, easy multi-GPU, simple code (about ~50 lines for the core).
What did they find, and why is it important?
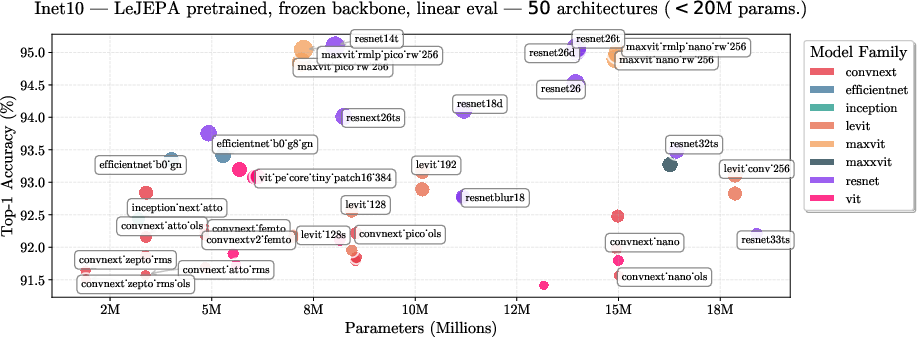
The authors tested LeJEPA on many datasets and model types (ResNets, ConvNets, ViTs, etc.), including very large models.
Key takeaways:
- Stable, simple training at scale: even giant models train smoothly without all the usual tricks.
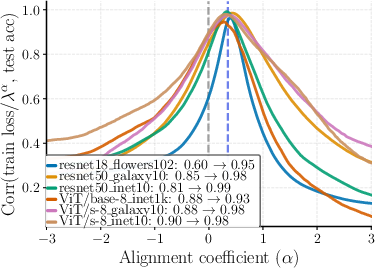
- Predictable model selection: the training loss strongly matches how well the features will do later with a simple linear probe, so you can pick good checkpoints without labels.
- Strong performance: for example, with ImageNet-1k pretraining and linear evaluation (frozen backbone), LeJEPA reaches about 79% with a ViT-H/14.
- Clear structure in features: when they reduce the features to visualize them, similar things cluster together sensibly (good sign the model learned meaning).
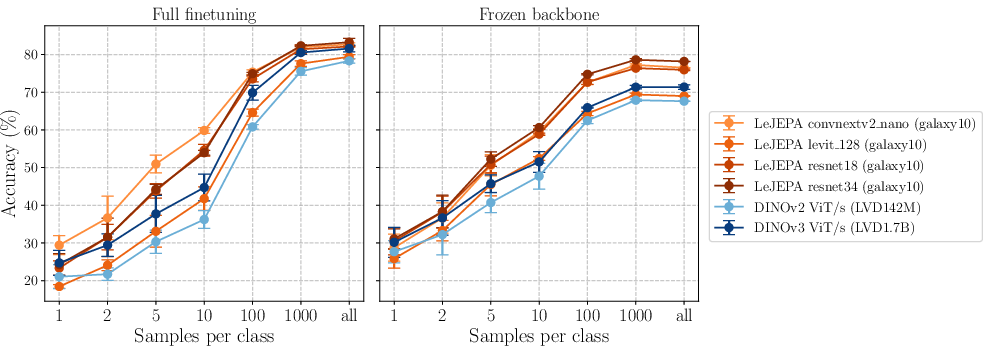
- In-domain beats big transfer: on domain-specific datasets (like Galaxy10, Food101), training LeJEPA directly on target-domain data outperforms transferring from very large general-purpose models (like DINOv2/v3). This suggests that smart, principled self-supervised pretraining can be a better choice than just copying features from massive generic models.
Why this matters:
- You get a clean, theory-backed way to prevent collapse and organize features optimally for many future tasks.
- It simplifies self-supervised learning: fewer hacks, fewer hyperparameters, more reliability.
- It works across architectures and data types.
Why it matters for the future
LeJEPA shows that:
- Theory can guide practice: by proving the best shape for the feature distribution (isotropic Gaussian), the authors designed a training method that’s both simpler and better.
- Self-supervised learning can be both scalable and robust without a pile of heuristics.
- For specialized fields (like astronomy images), training your own model with LeJEPA may beat importing a giant, generic model — making good AI more accessible to smaller domains and teams.
In short, this paper helps move self-supervised pretraining from “fragile recipes and tricks” to a simple, principled method that works across scales, models, and domains.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or left unexplored in the paper, framed so future researchers can act on each item.
- Scope of “optimality” for isotropic Gaussian embeddings: Theoretical results are derived for linear probes and specific nonlinear estimators (radius-based k-NN, Nadaraya–Watson kernels) under covariance trace/Frobenius constraints. It remains unproven whether isotropic Gaussian is uniquely optimal for broader real-world probe families (e.g., logistic regression with cross-entropy, margin-based classifiers, shallow MLP heads, SVMs, decision trees) and metric choices (cosine vs. Euclidean).
- Task-dependent deviations from isotropy: Many downstream problems benefit from anisotropic or structured (e.g., hierarchical, clustered, low-rank) embeddings. The paper does not examine whether forcing global isotropy can degrade tasks that need class-conditional anisotropy, cluster separability, or mixture distributions, nor how to reconcile isotropy with such demands.
- Impact on unit-normalized/cosine-similarity embeddings: A large fraction of JEPA/contrastive methods normalize embeddings to the unit sphere and optimize cosine similarity. The consequences of enforcing an isotropic Gaussian target (rather than a uniform-on-sphere/Watson distribution) for normalized embeddings are not analyzed.
- Finite-sample guarantees and sample complexity: While the sketching via 1D projections and Cramér–Wold arguments provide asymptotic validity, there are no finite-sample bounds for the number of directions M, batch size N, and embedding dimension K required to reliably detect/decrease anisotropy or non-Gaussianity.
- Averaging vs. max aggregation in SIGReg: The hypothesis test consistency is proved for the max over directions, but SIGReg uses an average to avoid sparse gradients. There is no theory quantifying how averaging affects test level/power, false-positive control, and convergence guarantees when used as a loss.
- Sensitivity to SIGReg hyperparameters and discretization: Despite “hyperparameter-free” claims, SIGReg entails choices (number of slices M, CF bandwidth σ, integration grid t, random-seed strategy). There is no sensitivity analysis, principled defaults, or guidelines for scaling these with K, N, architecture, and domain; nor error bounds for the integral discretization.
- Stability under heavy-tailed or non-Gaussian target regimes: The Epps–Pulley CF test is proposed toward a standard normal. Robustness to heavy tails (e.g., Student-t), skewed/elliptical targets, or outliers is not studied. It remains unclear whether a robust/elliptical target distribution would sometimes be preferable and how to implement it.
- Curse-of-dimensionality claims need rates: The paper asserts SIGReg “defeats” the curse via random projections and Sobolev smoothness, but provides no quantitative rates linking smoothness, dimension, and M to detection power or convergence speed.
- Interaction with JEPA predictive loss and collapse: While the paper claims collapse is “eliminated by construction,” there is no formal joint optimization analysis ruling out degenerate solutions where embeddings match the Gaussian target yet carry insufficient information to satisfy prediction tasks (or vice versa). Formal guarantees for the combined objective are missing.
- Choice of views and predictive objective details: The predictive component (“JEPA loss”) is under-specified (types of views/augmentations, whether asymmetric predictors are used, masking setup, specific loss form). The generality of stability and performance claims across different view designs/modalities remains untested.
- Generalization beyond images and in-domain datasets: Empirical validation appears concentrated on image classification/linear evaluation and a few domain-specific datasets (e.g., Galaxy10, Food101). There is no evidence or analysis for text, audio, video, robotics/control, multiview/multimodal data, retrieval, detection/segmentation, or generative tasks.
- Comparison breadth and standardization: Performance claims vs. “state-of-the-art” are shown selectively (e.g., DINOv2/v3). A comprehensive, standardized benchmark suite (multiple tasks, modalities, and training scales) with protocol-aligned baselines (SimCLR/BYOL/VICReg/DINO variants) is absent.
- Effect on separability and class-conditional structure: Forcing global isotropy may compress or distort class clusters. There is no quantitative paper of between-class separability, margin distributions, or cluster geometry under SIGReg compared to whitening or feature decorrelation methods (e.g., VICReg, W-MAE).
- Guidance for the single trade-off hyperparameter: The paper emphasizes a single weighting between JEPA and SIGReg losses but does not offer principled selection methods, scaling rules, or auto-tuning strategies to balance informativeness and Gaussification across architectures/data scales.
- Distributed training and communication overhead: Although the ECF is “DDP-friendly,” there is no analysis of communication costs, scaling behavior (world size, mixed precision), or potential bottlenecks of the all-reduce step for large M and t grids.
- Potential implementation inconsistency in code listing: The provided SIGReg pseudo-code samples projection vectors A but appears to compute the ECF on x directly without applying A (i.e., missing z = x @ A). This raises uncertainty about the correctness of the minimal implementation and reproducibility details.
- Choice of CF weighting/window function: The CF weight w(t) and σ are important for test sensitivity and gradient properties. There is no paper of alternative windows (e.g., Laplace, Tukey) or adaptive bandwidth selection and their impact on training stability/power.
- Finetuning vs. frozen evaluation: Results emphasize frozen linear probes. The behavior of SIGReg under full fine-tuning (catastrophic forgetting, representation reshaping), few-shot adapters, or task-specific heads is not analyzed.
- Robustness to batch size and optimizer settings: Stability claims do not report behavior under extreme batch sizes (very small or very large), various optimizers (AdamW/LARS), learning-rate schedules, or regularization schemes (weight decay, gradient clipping).
- Theoretical alignment with whitening/normalization layers: The relation between SIGReg’s isotropy enforcement and standard feature-normalization/whitening (BN/LayerNorm/Projector whitening) is not derived. Whether SIGReg complements or redundantly overlaps these mechanisms remains unclear.
- Downstream risk formalization beyond ISB: The nonlinear analysis focuses on integrated squared bias. Practical tasks often hinge on classification error, margin distributions, calibration, or retrieval metrics. Mapping isotropic Gaussian optimality to those metrics is not established.
- Adversarial robustness and safety implications: The effect of isotropic Gaussified embeddings on adversarial vulnerability, robustness, and safety (e.g., spurious correlation suppression, fairness) is unstudied.
- Custom target distributions and task-aware regularization: Although SIGReg can, in principle, target arbitrary Q, the paper focuses only on isotropic Gaussian. Open questions include how to pick Q systematically given task priors (e.g., mixture models, sparse priors), and whether adaptive/learned targets improve performance.
- View of modality-agnostic scaling limits: Claims of linear complexity emphasize minibatch size N but do not quantify scaling in K, M, and t (and their practical upper bounds) nor memory footprints for billion-parameter encoders on typical hardware.
Practical Applications
Immediate Applications
Below are concrete use cases that can be deployed now based on the paper’s findings and released code, grouped by sector and including assumptions or dependencies that might affect feasibility.
- Industry (software/AI): Replace brittle SSL heuristics with LeJEPA+SIGReg in existing pretraining pipelines
- What: Swap stop-gradient, teacher–student (EMA), whitening, and negative-sample heuristics with the single LeJEPA objective (JEPA predictive loss + SIGReg).
- Why: Linear time/memory complexity, distributed training-friendly, stable across architectures (ResNets, ViTs, ConvNets).
- Tools/workflows: Integrate the provided ~50-line PyTorch SIGReg implementation with Epps–Pulley statistic into DDP training; use the JEPA predictive view setup already in your pipeline.
- Assumptions/dependencies: Requires a reasonable view-generation strategy (augmentations, masking/cropping) and minibatch IID assumptions; isotropic Gaussian enforcement is optimal for broad downstream tasks but some niche applications may prefer domain-specific anisotropic geometries.
- MLOps (cross-sector): Unsupervised model selection and early stopping via training loss
- What: Use LeJEPA’s training loss (predictive + SIGReg) as a proxy for downstream linear-probe performance, eliminating supervised probing during pretraining.
- Why: The paper shows strong correlation between training loss and linear evaluation accuracy on ImageNet-1k (e.g., ViT-base), enabling label-free checkpointing and early stopping.
- Tools/workflows: Monitoring dashboards that track SIGReg+JEPA loss; automatic checkpoint ranking; fewer supervised validation runs.
- Assumptions/dependencies: Correlation demonstrated for linear probes and JEPA settings; generalization to other probes and domains is likely but should be spot-checked.
- Domain-specific SSL (healthcare, manufacturing, astronomy, remote sensing): In-domain pretraining that beats out-of-domain transfer
- What: Pretrain LeJEPA directly on the target domain (e.g., radiology images, defect images, telescope imagery, satellite scenes) and then apply frozen or linear probes.
- Why: Paper shows LeJEPA’s in-domain pretraining outperforms DINOv2/v3 transfer on Galaxy10 and Food101 across 1-shot to full supervision regimes.
- Tools/products: Domain-focused foundation backbones for medical imaging PACS, AOI/visual inspections, telescope pipelines, and EO imagery; frozen backbones + simple probes.
- Assumptions/dependencies: Requires enough unlabeled domain data and sensible view definitions; isotropic Gaussian enforcement is beneficial when downstream task families are diverse or unspecified; clinical/manufacturing validation still required.
- Retrieval/search systems (software, e-commerce, media): More reliable k-NN and kernel-based retrieval with isotropic Gaussian embeddings
- What: Use LeJEPA embeddings to power product or media search (image/text pairs via JEPA views), benefiting k-NN and kernel estimators that prefer well-conditioned latent geometries.
- Why: Theoretical results show isotropic Gaussian embeddings reduce estimator bias/variance for k-NN and kernel predictors; practical improvements in stability and generalization.
- Tools/workflows: Vector databases (FAISS/ScaNN) with LeJEPA embeddings; simple hyperparameter regimes; fewer post-hoc normalization tricks.
- Assumptions/dependencies: Quality of views (augmentations) and JEPA pairing impacts semantic alignment; for multimodal cases, views must preserve semantic correspondences.
- Robotics (software/robotics): Stable self-supervised predictive representation learning without teacher–student
- What: Use LeJEPA to learn manipulable world models from robot sensor streams via JEPA predictive views (e.g., temporal neighbors, action-conditioning), and SIGReg to avoid collapse.
- Why: Removes fragile EMA schedules and stop-gradients while scaling easily to high-dimensional embeddings; bounded gradients via Epps–Pulley.
- Tools/workflows: JEPA predictive objectives over time steps; SIGReg for distribution matching; frozen backbones with simple controllers or probes.
- Assumptions/dependencies: View design (temporal, multimodal, action-conditioned) must reflect task dynamics; isotropic enforcement assumes broad task families post-training.
- Academic research (machine learning): Theory-driven SSL baselines and course materials
- What: Adopt LeJEPA as a clean, reproducible baseline for SSL without heuristics; teach JEPA+SIGReg as a principled approach grounded in hypothesis testing and Cramér–Wold projections.
- Why: Promotes theory-to-practice designs; simplifies experimental comparisons across 60+ architectures and 10+ datasets.
- Tools/workflows: GitHub repo; lecture modules on isotropic Gaussian optimality, CF-based tests, and JEPA design.
- Assumptions/dependencies: Research adoption depends on available compute and datasets; further extensions may be needed for specialized modalities.
- Energy and sustainability (operations): Reduce compute waste from brittle SSL training
- What: Limit repeated failed runs and extensive hyperparameter sweeps by using LeJEPA’s single trade-off parameter and stable training dynamics.
- Why: Fewer reruns and less tuning reduce energy and cost footprints.
- Tools/workflows: Standardized training templates with LeJEPA; automated loss-based checkpoint selection.
- Assumptions/dependencies: Actual savings depend on current pipeline complexity; benefits scale with organization size and model scale.
- Finance and time series (analytics): Better-conditioned embeddings for downstream regressors/classifiers
- What: Apply LeJEPA to high-dimensional event logs or multivariate time series to produce embeddings that improve linear/logistic regression stability and k-NN risk.
- Why: Isotropy reduces estimator variance/bias in linear and nonlinear probes.
- Tools/workflows: JEPA views from temporal slicing or multi-sensor streams; frozen backbones + linear probes for risk modeling.
- Assumptions/dependencies: JEPA views must capture temporal/structural relationships; stationarity and IID assumptions affect performance.
Long-Term Applications
These use cases require further research, scaling, domain validation, or ecosystem development before broad deployment.
- Healthcare (medical imaging foundation models): Clinical-grade in-domain SSL backbones
- What: Build hospital-specific backbone models via LeJEPA pretraining on local unlabeled scans; deploy frozen backbones with lightweight probes across tasks (classification, detection).
- Why: Potentially better than web-scale transfer while respecting data privacy and distributional shifts.
- Tools/products: “Hospital LeJEPA” appliances; privacy-preserving pipelines with on-prem training; regulatory documentation.
- Assumptions/dependencies: Requires rigorous clinical validation, safety audits, and regulatory approvals; robust view design for medical modalities.
- Multimodal foundation models (vision–language–audio–sensor fusion)
- What: Standardize latent geometries across modalities by enforcing isotropic Gaussian embeddings, simplifying alignment, fusion, and downstream k-NN/kernel tasks.
- Why: Better-conditioned shared latent spaces can ease cross-modal retrieval and few-shot transfer.
- Tools/products: Multimodal LeJEPA frameworks with SIGReg applied per modality and across joint embeddings.
- Assumptions/dependencies: Needs principled multimodal JEPA view designs; careful handling of modality-specific anisotropies; thorough cross-modal evaluations.
- Robotics (policy/control): End-to-end world models for planning with fewer heuristics
- What: Leverage stable LeJEPA embeddings for predictive control and planning in complex environments (manipulation, navigation).
- Why: Replaces brittle teacher–student pipelines; bounded gradients aid long-horizon optimization.
- Tools/products: “LeJEPA Control” libraries integrating JEPA views with action-conditioned predictors and SIGReg; sim-to-real workflows.
- Assumptions/dependencies: Requires large-scale, action-rich datasets and robust evaluation; domain-specific view engineering remains key.
- Edge/on-device SSL (software/hardware): Lightweight pretraining without heavy orchestration
- What: Use linear-complexity SIGReg to bring parts of SSL pretraining onto edge devices (industrial cameras, mobile), reducing reliance on cloud-scale heuristics.
- Why: Bounded gradients and simple implementation could translate to more predictable resource use.
- Tools/products: Edge-optimized LeJEPA runtimes; hardware-aware projection sampling; intermittent training workflows.
- Assumptions/dependencies: Hardware constraints and memory bandwidth; need for efficient random projection sampling and CF integration on-device.
- Policy and governance (public sector, enterprise): Encouraging in-domain pretraining over generic transfer
- What: Shift procurement and data governance toward secure, domain-specific SSL pretraining (LeJEPA) rather than generic web-scale model reliance.
- Why: Aligns with privacy, sovereignty, and distributional fit; may reduce data movement and legal exposure.
- Tools/workflows: Policy guidance, procurement standards, internal governance playbooks for domain SSL.
- Assumptions/dependencies: Organizational capability to curate unlabeled domain data and define JEPA views; costs vs. benefits depend on scale and risk profile.
- AutoML and hyperparameter-light training platforms
- What: Integrate LeJEPA as a default SSL objective with a single trade-off hyperparameter, reducing tuning complexity for varied architectures and datasets.
- Why: Operational simplicity for broad users; faster iteration cycles.
- Tools/products: “LeJEPA Trainer” modules in major AutoML frameworks; loss-based model selection baked in.
- Assumptions/dependencies: Widespread adoption requires benchmarks across modalities and tasks; integration work with existing AutoML ecosystems.
- Standardization and auditing (quality/compliance): “Gaussianity audits” for embeddings
- What: Create auditing tools to verify isotropic Gaussianity of embeddings during training/serving, flagging collapse or geometric drift.
- Why: Practical diagnostics for representation health in production.
- Tools/products: SIGReg-based monitors; compliance reports for ML governance.
- Assumptions/dependencies: Agreement on audit thresholds and test protocols; domain-specific allowances for controlled anisotropy.
- Education and workforce development
- What: Curriculum and certification around theory-grounded SSL (JEPA + SIGReg), focusing on hypothesis testing, characteristic functions, and Cramér–Wold projections.
- Why: Builds capacity for robust, heuristic-free AI development.
- Tools/products: Courseware, labs, and standardized exercises using the official LeJEPA codebase.
- Assumptions/dependencies: Broad academic and industry buy-in; continuous updates to reflect multimodal and domain-specific advances.
Glossary
- all_reduce: A distributed collective operation that reduces tensors across processes (e.g., by averaging) to synchronize values in multi-GPU training. "ecf = all_reduce(ecf, op=\"AVG\")"
- Anderson Darling: A goodness-of-fit test that emphasizes discrepancies in the tails of a distribution’s cumulative distribution function. "and Anderson Darling \citep{anderson1952asymptotic},"
- Backward Cramér-Wold Statistics: A projection-based objective that tests distributional alignment by comparing 1D projected densities against a target. "Our proposed Backward Cramér-Wold Statistics (\cref{sec:bcs}) objective pushes to match a target distribution "
- CDF (Cumulative Distribution Function): A function giving the probability that a random variable is less than or equal to a value; used in several classical goodness‑of‑fit tests. "The second family of tests acts upon the CDF."
- Characteristic function: The Fourier transform of a probability distribution, used to compare empirical data to a target distribution via stable, differentiable statistics. "distributional alignment via random projections and characteristic-function matching"
- Cramér-von Mises: A CDF-based goodness‑of‑fit test measuring squared deviations between empirical and target CDFs with uniform weighting. "known as Cramér-von Mises \citep{cramer1928composition,von1981probability}"
- Cramér-Wold theorem: A foundational result stating two multivariate distributions are equal if all their 1D projections are equal in distribution. "and a slightly modified Cramér-Wold theorem."
- Curse of dimensionality: The degradation of statistical and computational efficiency as dimensionality grows, affecting high‑dimensional distribution matching. "defeats the curse of dimensionality"
- DDP (Distributed Data Parallel): A training paradigm that replicates models across devices and synchronizes gradients to scale SGD efficiently. "DDP-friendly and scalable"
- ECF (Empirical Characteristic Function): An empirical estimate of the characteristic function computed as an average of complex exponentials over samples. "Empirical Characteristic Functions (ECF) which are the Fourier transform of the density function."
- EMA (Exponential Moving Average): A smoothed update rule often used for teacher parameters in self‑supervised training schedules. "teacherâstudent networks with carefully tuned EMA schedules"
- Epps–Pulley test: A characteristic‑function‑based normality test comparing empirical and theoretical CFs with a weighting window. "The EppsâPulley test \citep{epps1983test} is one of the most popular test"
- Feature whitening: A transformation that decorrelates and scales features to unit variance, often used to stabilize representation learning. "feature whitening \citep{ermolov2021whitening,bardes2021vicreg}"
- Hypothesis testing: A statistical framework to assess evidence against a null (e.g., distributional equality), controlling Type I error via a critical value. "Consider the hypothesis testing framework"
- Isotropic Gaussian: A multivariate normal distribution with identical variance along all dimensions and zero cross‑covariances. "we identify the isotropic Gaussian as the optimal distribution"
- Jarque–Bera: A moment‑based normality test that uses skewness and kurtosis to assess deviations from Gaussianity. "Jarque-Bera \citep{jarque1980efficient} test"
- JEPA (Joint-Embedding Predictive Architectures): A self‑supervised framework that trains encoders by enforcing predictive agreement between embeddings of related views. "Joint-Embedding Predictive Architectures (JEPAs) offer a promising blueprint"
- Kernel methods: Nonparametric techniques that estimate functions (e.g., for regression) by locally averaging with a kernel weighting scheme. "and kernel methods \citep{nadaraya1964estimating,watson1964smooth}"
- k-NN (radius-based): A nonparametric predictor that averages labels of neighbors within a fixed radius of the query in embedding space. "radius-based k-NN \citep{taunk2019brief,sun2010adaptive,zhang2017efficient,abu2019effects}"
- Kolmogorov–Smirnov: A CDF-based goodness‑of‑fit test using the maximum deviation between empirical and theoretical CDFs. "We do not consider the Kolmogorov-Smirnov test \citep{kolmogorov1933}"
- Latent-Euclidean JEPA (LeJEPA): A JEPA design that enforces an isotropic Gaussian latent space via SIGReg, eliminating collapse with a single hyperparameter. "coined Latent-Euclidean JEPA (LeJEPA)"
- Mutual Information (MI): A measure of statistical dependence between random variables, often used to motivate contrastive objectives and SSL theory. "those studies involve the {\em Mutual Information (MI)}"
- Order statistics: The sorted values of a sample (e.g., kth smallest), used in many CDF-based tests. "denote the order-statistics of samples"
- Predictive coding: A representation learning paradigm where the model predicts future or missing information from current observations. "predictive coding \citep{helmholtz1867handbook,bruner1949perception}"
- Push-forward distribution: The distribution of a random variable after applying a mapping (e.g., projection), central to directional testing. "Denoting the push-forward distributions $P_^{()} \triangleq (^\top)_\# P_$"
- Representation collapse: A failure mode where embeddings become degenerate (identical or low‑dimensional), harming downstream performance. "representation collapse, where maps all inputs to nearly identical embeddings"
- Shapiro–Wilk test: A classical normality test based on correlation of order statistics with expected normal scores. "Another common test is the Shapiro-Wilk test \citep{shapiro1965analysis}"
- SIGReg (Sketched Isotropic Gaussian Regularization): A scalable regularization objective that enforces isotropic Gaussian embeddings via projected statistical tests. "Sketched Isotropic Gaussian Regularization (SIGReg)"
- Siamese networks: Twin encoders with shared weights that produce comparable embeddings for related inputs. "siamese networks \citep{bromley1993signature}"
- Sobolev smoothness coefficient: A parameter quantifying smoothness of functions/distributions in Sobolev spaces, affecting projection coverage on the sphere. "with varying Sobolev smoothness coefficients ."
- Stop‑gradient: A training heuristic that prevents gradient flow through certain branches to avoid collapse or instability. "stopâgradient \citep{chen2020simple}"
- Teacher–student networks: SSL setups where a student network learns from a teacher’s targets, often stabilized with EMA. "teacherâstudent networks"
- Tikhonov regularization: L2‑penalized least squares that stabilizes linear probes by shrinking coefficients, controlled by a hyperparameter. "Tikhonov regularizer strength"
- Union–intersection principle: A statistical testing strategy that aggregates lower‑dimensional tests to assess a global multivariate hypothesis. "union-intersection principle \citep{roy1953heuristic}"
- Watson test: A CDF-based goodness‑of‑fit statistic that adjusts the Cramér‑von Mises measure by removing linear components. "recovers the Watson test \citep{watson1961goodness}"
Collections
Sign up for free to add this paper to one or more collections.