Leveraging Second-Order Curvature for Efficient Learned Image Compression: Theory and Empirical Evidence

Abstract: Training learned image compression (LIC) models entails navigating a challenging optimization landscape defined by the fundamental trade-off between rate and distortion. Standard first-order optimizers, such as SGD and Adam, struggle with \emph{gradient conflicts} arising from competing objectives, leading to slow convergence and suboptimal rate-distortion performance. In this work, we demonstrate that a simple utilization of a second-order quasi-Newton optimizer, \textbf{SOAP}, dramatically improves both training efficiency and final performance across diverse LICs. Our theoretical and empirical analyses reveal that Newton preconditioning inherently resolves the intra-step and inter-step update conflicts intrinsic to the R-D objective, facilitating faster, more stable convergence. Beyond acceleration, we uncover a critical deployability benefit: second-order trained models exhibit significantly fewer activation and latent outliers. This substantially enhances robustness to post-training quantization. Together, these results establish second-order optimization, achievable as a seamless drop-in replacement of the imported optimizer, as a powerful, practical tool for advancing the efficiency and real-world readiness of LICs.

• The paper introduces SOAP, a second-order quasi-Newton optimizer that speeds up LIC training and improves rate-distortion performance by 3% BD-Rate.
• It leverages theoretical insights on gradient alignment to overcome limitations of first-order methods and resolve gradient conflicts for smoother convergence.
• Empirical evidence shows SOAP reduces training steps by up to 70% and wall-clock time by 57.7% while suppressing activation outliers for robust compression.

Leveraging Second-Order Curvature for Efficient Learned Image Compression

This essay provides an in-depth analysis of the paper titled "Leveraging Second-Order Curvature for Efficient Learned Image Compression: Theory and Empirical Evidence" (2601.20769). The paper tackles the optimization challenges in training Learned Image Compression (LIC) models using a second-order quasi-Newton optimizer, SOAP. It presents theoretical and empirical evidence that this optimizer leads to faster convergence and improved rate-distortion performance compared to standard first-order methods.

Introduction to Learned Image Compression

Learned Image Compression (LIC) models optimize the rate-distortion (R-D) trade-off, which is a foundational challenge in image compression. LICs typically employ transform coding frameworks aiming to minimize reconstruction error (distortion) while reducing the bit rate needed for encoding the latent representation. Optimizing this trade-off has traditionally been approached using first-order optimizers like Adam, which struggle with gradient conflicts, leading to slow convergence and suboptimal performance.

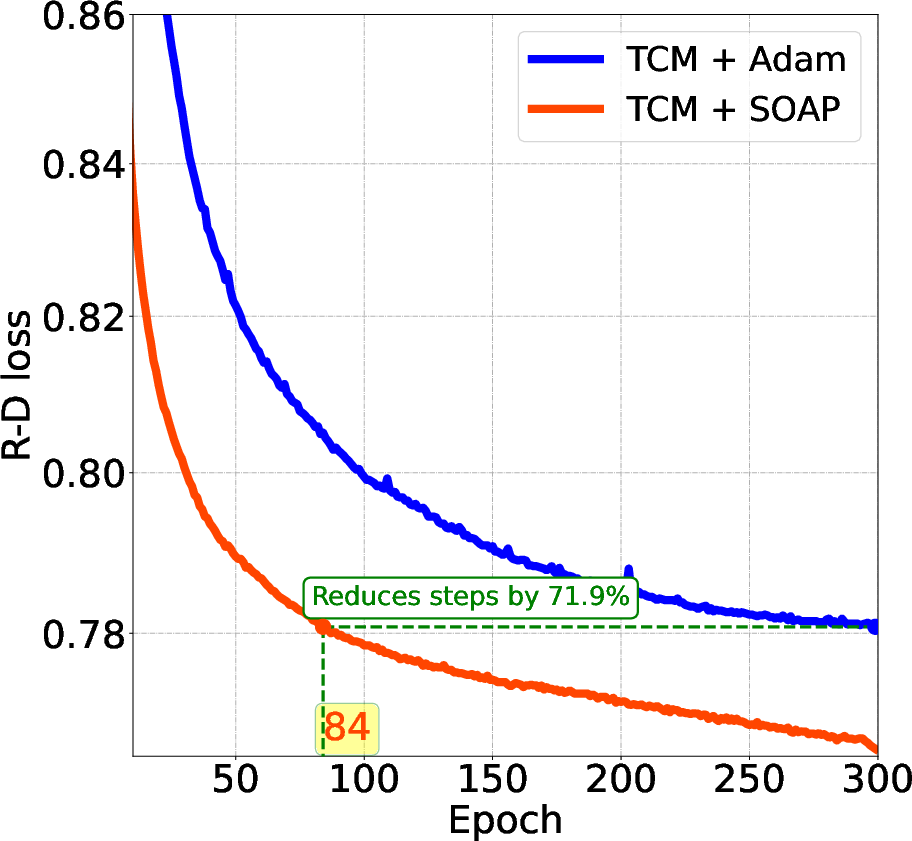
Figure 1: Comparison of Testing Loss: Epochs vs. R-D Loss for Various LICs. The SOAP optimizer demonstrates significantly faster convergence.

Second-Order Optimization with SOAP

The paper introduces SOAP as a second-order optimization alternative, which leverages Newton-style preconditioning. The authors hypothesize that by resolving intra-step and inter-step gradient conflicts, SOAP accelerates convergence and enhances the final compression performance of various state-of-the-art LIC models such as ELIC, TCM, and LALIC.

Empirical results confirm the superiority of SOAP, which achieves up to 70% reductions in training steps and 57.7% reductions in wall-clock time compared to Adam, while also delivering a 3% BD-Rate improvement in terms of rate-distortion efficiency. This highlights SOAP's capacity to navigate the complex optimization landscape more effectively.

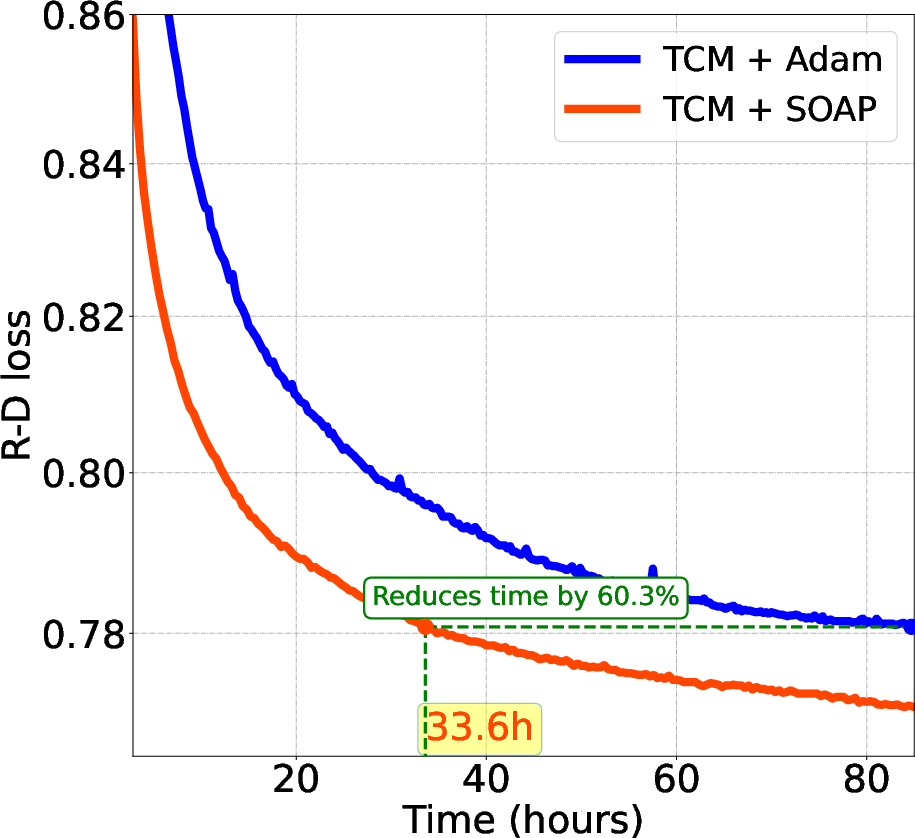
Figure 2: Comparison of Testing Loss: Wall-Time vs. R-D Loss for Various LICs.

Theoretical Insights: Gradient Alignment

The paper provides theoretical insights into why SOAP predicts more aligned gradient updates through curvature information. Newton preconditioning ensures that the optimizer aligns the conflicting rate and distortion gradients, overcoming the limitations of Adam's diagonal preconditioning. The intra-step and inter-step alignment achieved via SOAP significantly enhance optimization trajectories, providing smoother, faster convergence as demonstrated empirically.

Figure 3: Evolution of intra-step and inter-step gradient scores for ELIC trained with Adam vs. SOAP.

Suppression of Outliers

A key advantage of second-order optimization revealed in this paper is its ability to suppress outliers in activation and latent spaces, a critical factor for enhancing robustness to post-training quantization. SOAP-trained models show fewer extreme values in feature statistics, leading to improved deployability in resource-constrained environments due to reduced dynamic range concerns.

Empirical measurements of kurtosis and maximum median deviations substantiate this claim, showing that SOAP consistently yields lower outlier metrics across tested models, improving the range of model applicability without sacrificing compression quality.

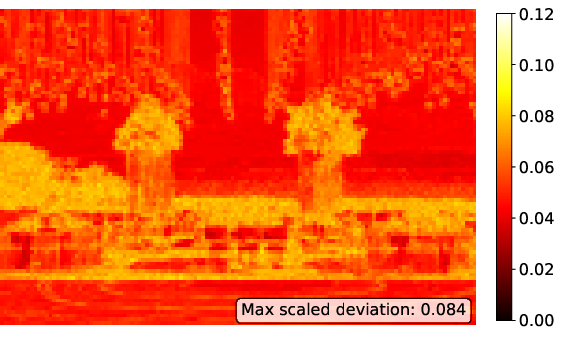
Figure 4: Scaled deviation maps for ELIC latent representations.

Comparison with Other Methods

SOAP's performance was compared to various LIC acceleration strategies like Auxiliary Transform (AuxT) and CMD-LIC, as well as gradient conflict mitigation methods like Balanced-RD. SOAP was found to outperform these methods in both convergence speed and compression quality, without introducing additional parameters or complex model alterations, emphasizing its practicality as a drop-in replacement optimizer.

Figure 5: SOAP shows faster convergence compared to various other optimizers and further improves when combined with AuxT.

Conclusion and Future Directions

The paper concludes that second-order optimization significantly enhances the training of LIC models, offering faster and more stable convergence, better rate-distortion trade-offs, and improved robustness to quantization outliers.

Future research directions suggested in the paper include hybrid optimization strategies that combine second-order information with other techniques, and extending second-order training to other formats such as video or 3D representation compression. The authors advocate leveraging optimization strategies as a critical pillar alongside architecture and algorithm design in learned compression research.

This essay summarizes the key contributions and implications of the study, providing a technical lens into the advancements brought by second-order optimization in the field of learned image compression.