Likelihood-Preserving Embeddings for Statistical Inference (2512.22638v1)

Abstract: Modern machine learning embeddings provide powerful compression of high-dimensional data, yet they typically destroy the geometric structure required for classical likelihood-based statistical inference. This paper develops a rigorous theory of likelihood-preserving embeddings: learned representations that can replace raw data in likelihood-based workflows -- hypothesis testing, confidence interval construction, model selection -- without altering inferential conclusions. We introduce the Likelihood-Ratio Distortion metric $Δ_n$, which measures the maximum error in log-likelihood ratios induced by an embedding. Our main theoretical contribution is the Hinge Theorem, which establishes that controlling $Δ_n$ is necessary and sufficient for preserving inference. Specifically, if the distortion satisfies $Δ_n = o_p(1)$, then (i) all likelihood-ratio based tests and Bayes factors are asymptotically preserved, and (ii) surrogate maximum likelihood estimators are asymptotically equivalent to full-data MLEs. We prove an impossibility result showing that universal likelihood preservation requires essentially invertible embeddings, motivating the need for model-class-specific guarantees. We then provide a constructive framework using neural networks as approximate sufficient statistics, deriving explicit bounds connecting training loss to inferential guarantees. Experiments on Gaussian and Cauchy distributions validate the sharp phase transition predicted by exponential family theory, and applications to distributed clinical inference demonstrate practical utility.

• The paper introduces a neural embedding method that preserves key log-likelihood information vital for robust statistical inference.
• It establishes theoretical guarantees, including the Hinge Theorem and Likelihood-Ratio Distortion metric, to ensure asymptotic inference fidelity.
• Empirical results demonstrate that low-dimensional embeddings achieve near-perfect inference performance in simulations and federated clinical trials.

Likelihood-Preserving Embeddings for Statistical Inference: Theory and Practice

Introduction and Motivation

The paper "Likelihood-Preserving Embeddings for Statistical Inference" (2512.22638) provides a rigorous theoretical and algorithmic framework for constructing neural embeddings that preserve all information requisite for likelihood-based inference. Conventional ML embeddings prioritize downstream prediction, often sacrificing the geometric and functional structure of log-likelihoods crucial for inferential statistics. This work formulates the problem of compressing high-dimensional data into fixed-length representations while retaining the entirety of likelihood-based inferential content—enabling standard workflows such as hypothesis testing, interval estimation, and model selection—particularly under stringent privacy, bandwidth, and computational constraints.

Theoretical Foundations

Central to the paper is the introduction of the Likelihood-Ratio Distortion metric $\Delta_n$, quantifying the worst-case error in log-likelihood ratios induced by an embedding. The authors establish the Hinge Theorem, demonstrating that bounding $\Delta_n = o_p(1)$ is both a necessary and sufficient condition to preserve likelihood-based inference: this guarantees that likelihood-ratio tests, maximum likelihood estimation, Bayes factors, and confidence intervals are asymptotically equivalent under the surrogate likelihood constructed from the embedding.

Pointwise approximation error $\varepsilon_n$—the maximum discrepancy between true and surrogate per-sample log-likelihoods—provides a sufficient criterion: $\varepsilon_n = o_p(1/n)$ ensures $\Delta_n \leq 2n\varepsilon_n = o_p(1)$, yielding strong preservation results for all standard inference procedures, including model selection via AIC/BIC. Empirically, this relationship is validated for exponential family models:

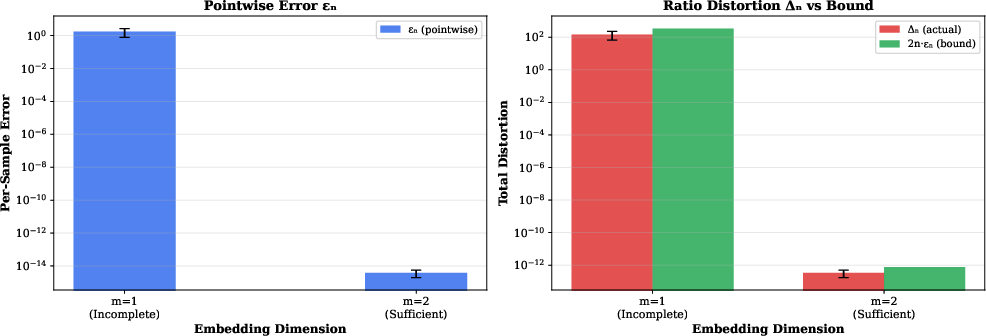
Figure 1: Empirical demonstration of the relationship $\Delta_n \leq 2n\varepsilon_n$ for Gaussian $\mathcal{N}(\mu,\sigma^2)$, confirming that controlling pointwise error suffices for ratio distortion.

A No Free Lunch theorem establishes that universal likelihood preservation is only possible for essentially invertible embeddings—hence, model-class-specific guarantees are imperative. For exponential families with $k$ parameters, the minimal embedding dimension is $k$; the framework recovers classical sufficiency as a limiting case.

Algorithmic Construction

The constructive recipe for likelihood-preserving embeddings employs neural networks: an encoder compresses each sample, a mean aggregation produces the dataset embedding, and a decoder predicts per-dataset log-likelihood given a candidate parameter. Training is performed by minimizing mean-squared error between true and surrogate log-likelihoods over parameter samples drawn from a relevant region in the parameter space. This pointwise loss explicitly enforces inferential sufficiency rather than predictive utility. The approach tunes the embedding to be insensitive to ancillary statistics, thereby recovering the property of completeness in exponential family settings.

Rigorous VC-dimension and complexity analysis yields PAC-style sample complexity bounds for training, though these are acknowledged to be loose compared to practical deep learning regimes.

Empirical Evaluations

The experimental section provides comprehensive validation:

1. Sufficient Statistic Recovery and Phase Transition

For Gaussian models, the sharp transition occurs at $m=2$, matching the number of sufficient statistics (mean and variance):

Figure 2: Gaussian (exponential family): sharp transition at $m=2$; both pointwise error $\varepsilon_n$ and distortion $\Delta_n$ drop to machine precision, confirming sufficiency.

For Cauchy models (non-exponential family), no finite embedding provides zero distortion, but information loss decays smoothly with increased embedding dimension.

2. Neural Embedding for GMMs

Neural networks trained with the likelihood-ratio distillation objective compress high-dimensional samples into low-dimensional embeddings with precise preservation of likelihood surfaces. For a $d=30$ parameter mixture model, a 16-dimensional embedding achieves $\varepsilon_n = 0.11$, $\Delta_n = 0.21$, and $r = 0.987$ correlation between surrogate and true log-likelihoods:

Figure 3: Neural embedding for a Gaussian mixture model achieves near-perfect preservation of log-likelihoods and ratios, validating the practical efficacy of the approach.

3. Distributed Clinical Trials

In a federated setting with five hospitals, computation of sufficient statistics enables pooled likelihood inference with only 16 transmitted numbers per site (100-fold data reduction, <1% loss in inferential power); even an aggressively compressed 8-dimensional summary retains 99% relative efficiency. Standard meta-analytic approaches are shown to incur a 50% power loss:

Figure 4: Multi-site clinical trial simulation: summary-based likelihood inference recovers gold-standard power, while meta-analysis suffers 50% loss; 8-dimensional compressed embeddings preserve near-perfect power.

Implications and Future Directions

Practically, this framework provides robust, deployable methods for distributed statistical inference under privacy and communication constraints, outperforming meta-analysis in both efficiency and accuracy. Theoretically, it sharpens the boundary between prediction-centric and inference-centric representation learning, elucidating when and how low-dimensional compression is permissible without undermining statistical validity.

Key implications and speculative directions include:

• Privacy-preserving inference: Enables exact likelihood-based testing without raw data sharing, with potential applications in genomics, finance, and cross-institutional research.
• Extension to simulator-based inference: Prospective integration of neural ratio estimation could adapt the framework for likelihood-free settings, although statistical guarantees would be less tractable.
• Model class dependence and robustness: Guarantees hinge on correct model class specification; adversarial training and robust selection of $F$ remain open areas.
• Automated selection of embedding dimension: Cross-validation on $\Delta_n$ or $\varepsilon_n$ for minimal sufficient embedding remains a practical device.

Conclusion

This work provides a unified treatment of likelihood-preserving embeddings, establishing precise theoretical criteria and concrete neural architectures for data compression that remains sufficient for all likelihood-based inference. The implications span privacy-preserving science, federated learning, and algorithmic statistics, marking a decisive step toward principled inferential procedures in the era of deep representation learning.