- The paper introduces an analytically tractable Bayesian regression model that quantifies how inference-time sample count and temperature affect generalization error.
- It employs reward-weighted sampling and extreme value theory to derive scaling laws, showing error decay as Θ(1/k²) under optimal conditions.
- Empirical validations with Meta-Llama-3-8B-Instruct and Mistral-7B-Instruct demonstrate practical benefits of reallocating computational resources from training to inference.
"Demystifying LLM-as-a-Judge: Analytically Tractable Model for Inference-Time Scaling" (2512.19905)
Introduction and Motivation
LLMs have demonstrated significant advancements by reallocating computational resources from training to inference time. Despite the observed benefits, the underlying principles of inference time scaling have remained underspecified. This paper introduces an analytically tractable model applied to the LLM-as-a-judge scenario to elucidate the inference-time scaling. The authors leverage Bayesian linear regression with a reward-weighted sampler and perform their analysis within the high-dimensional regime. Specifically, they explore this setup in scenarios where training samples originate from a teacher model and inference performance is judged by an LLM acting as a judge.
Analytical Framework and Methodology
The authors build their model on Bayesian regression, where the output prediction of an input vector is influenced by a teacher model and further perturbed by Gaussian noise. The LLM-as-a-judge framework is embodied by incorporating reward-driven inference-time sampling, wherein multiple inference samples are drawn. Each sample is scored using a reward metric based on its consistency with a teacher-model-aligned reward function.
Critical to this study is analyzing how parameter choices, such as the number of inference-time samples k and the sampling temperature T, influence generalization error. Through deterministic equivalents, the authors derive expressions for the posterior predictive mean and variance, offering insights into optimizing inference-time decisions with these parameters.

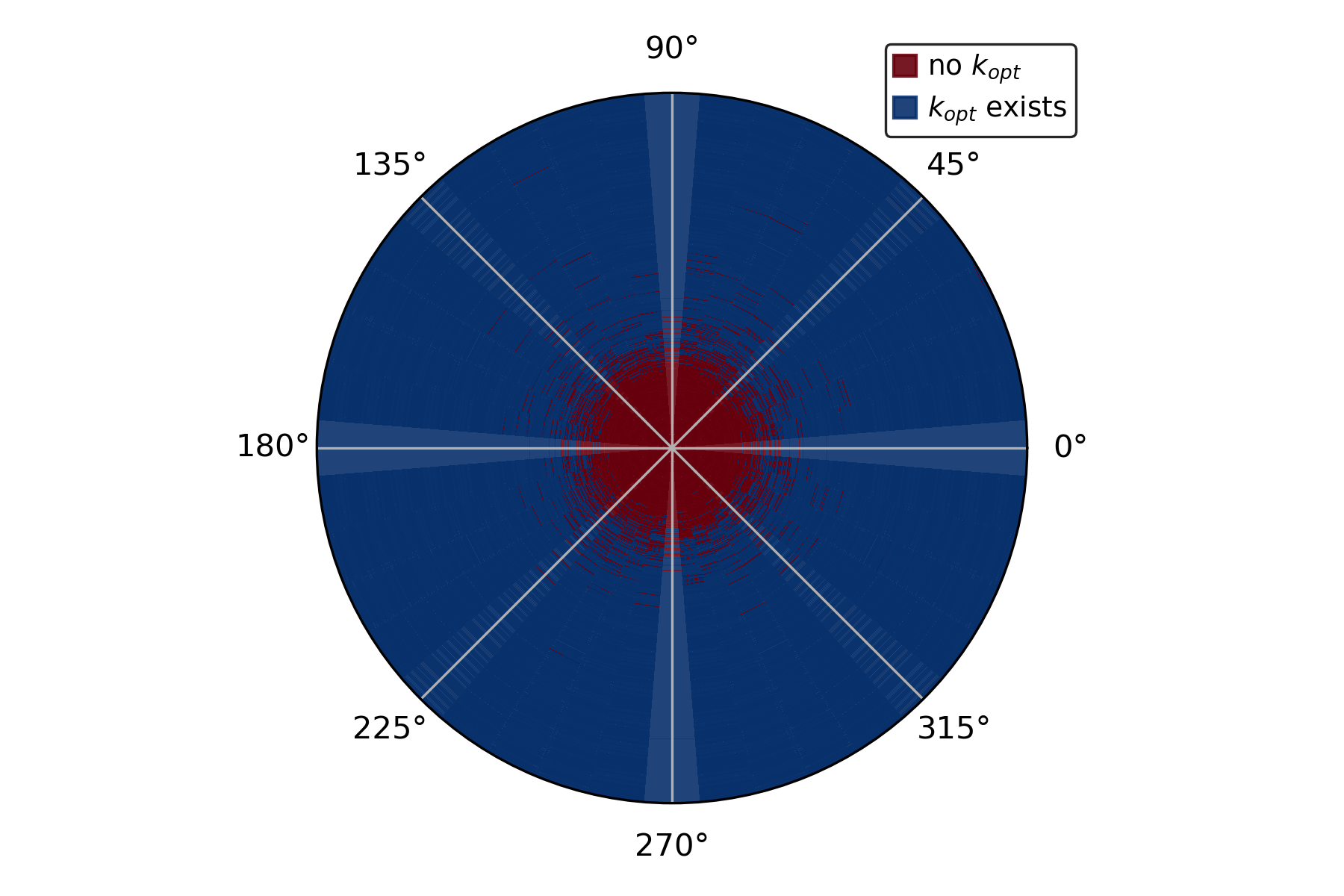
Figure 1: T=20 σ2
Results and Empirical Validation
Through extensive experiments aligned with theoretically derived predictions, the study provides several key findings:
- Generalization Error Decay: When the reward aligns closely with the teacher model, generalization error monotonically decreases as the number of inference-time samples k rises.
- Reward Misspecification Impact: With substantial reward misalignment, an optimal k emerges, beyond which further sampling increases generalization error.
- Temperature Influence: An optimal temperature T exists for a fixed k, maximizing the reward effectiveness while minimizing the generalization error.
- Scaling Laws: In optimal conditions (i.e., best-of-k scenario), generalization error decreases as Θ(1/k2). This finding, derived using extreme value theory, delineates scenarios where inference-time scaling is more efficient than mere data expansion.
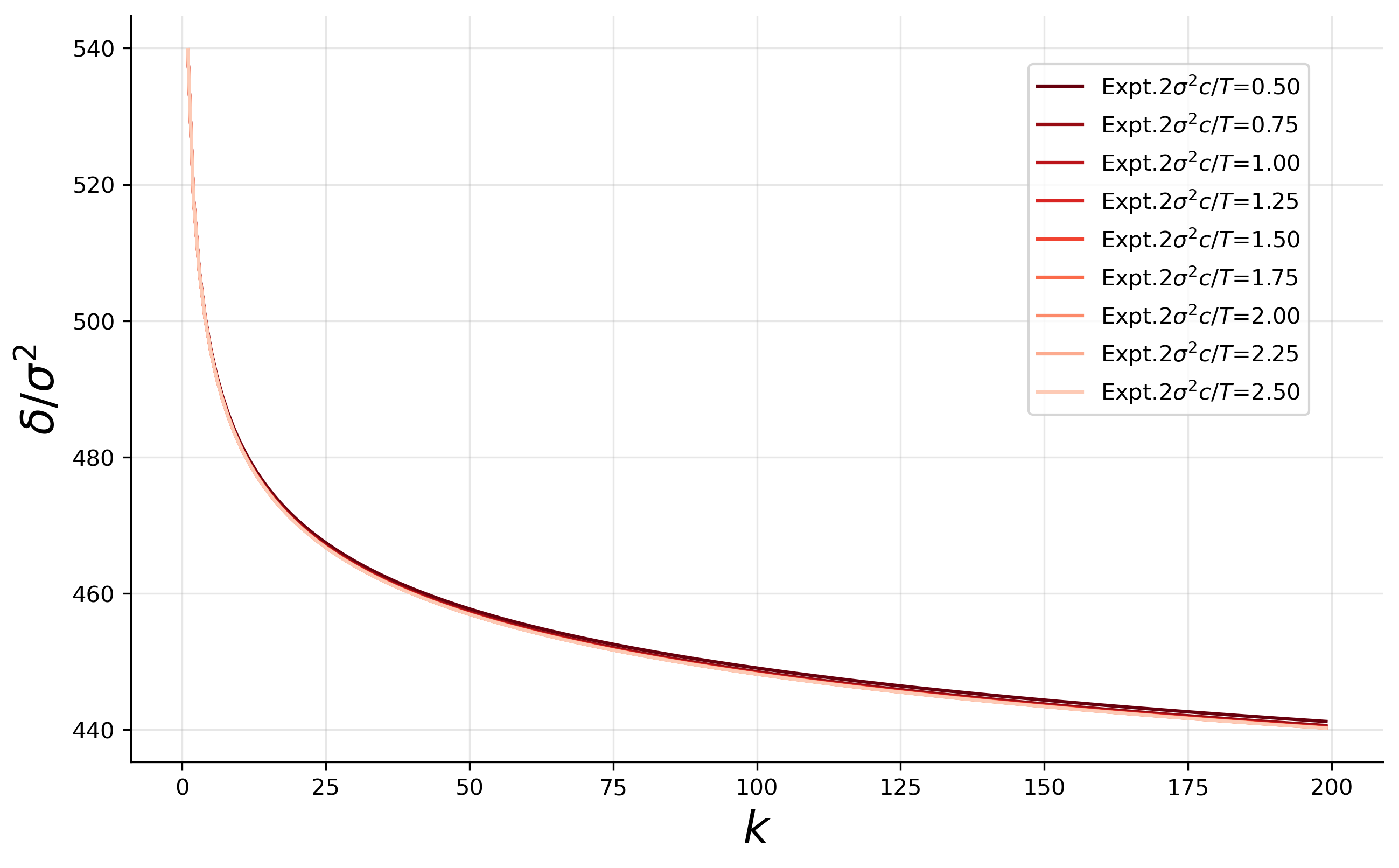
Figure 2: S=100
Implications and Future Directions
The implication of these results is profound for practical applications of LLMs. The research identifies where shifting computational resources to inference-time can significantly improve performance without further data collection. Such findings are crucial for domains where collecting additional training data may be resource-intensive or impractical.
Theoretical developments include quantifying the degradation of inference-time efficiency with increasing task difficulty. Furthermore, empirical validation using models like Meta-Llama-3-8B-Instruct and Mistral-7B-Instruct corroborated the theoretical insights.
This work lays the groundwork for future explorations into how inference-time computations can be strategically enhanced. It prompts an investigation into more complex reward structures and their impact on broader AI systems, potentially leading to more robust architectures capable of real-time adaptation.
Conclusion
This paper elucidates critical aspects of inference-time scaling in LLMs through a systematic and analytical approach. By modeling the LLM-as-a-judge scenario, the authors provide a comprehensive framework for understanding and optimizing the allocation of computational resources at inference time. The insights derived here are not only theoretically enriching but hold practical promise for advancing the efficiency and performance of AI models in complex settings.




