Best-of-$\infty$ -- Asymptotic Performance of Test-Time Compute (2509.21091v1)
Abstract: We study best-of-$N$ for LLMs where the selection is based on majority voting. In particular, we analyze the limit $N \to \infty$, which we denote as Best-of-$\infty$. While this approach achieves impressive performance in the limit, it requires an infinite test-time budget. To address this, we propose an adaptive generation scheme that selects $N$ based on answer agreement, thereby efficiently allocating inference-time computation. Beyond adaptivity, we extend the framework to weighted ensembles of multiple LLMs, showing that such mixtures can outperform any individual model. The optimal ensemble weighting is formulated and efficiently computed as a mixed-integer linear program. Extensive experiments demonstrate the effectiveness of our approach.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper looks at a simple way to make LLMs more accurate: ask them the same question many times and pick the answer that shows up most often (this is called “majority voting” in “Best-of-N”). The authors paper what happens if you could do this with an unlimited number of tries (they call this “Best-of-∞”) and then design a smart, practical method that gets close to that ideal without wasting tons of computation. They also show how combining several different LLMs, with the right mixing weights, can beat any single model.
Key questions the paper asks
- How much better can models get if we ask them multiple times and vote on the answer?
- Since we can’t try infinitely many times, how can we stop early once we’re confident enough?
- Can mixing multiple different LLMs, each with its own strengths, outperform the best single model? And how do we find the best mix?
How they did it (methods, explained simply)
1) Best-of-N and Best-of-∞
Imagine asking a friend a tough question many times. If you take the answer you hear the most, you usually do better than trusting just one try. If you could ask infinite times, you’d get the most reliable majority answer possible. But infinite tries aren’t realistic, so the goal is to get close to that with a smart stopping rule.
2) Adaptive stopping: stop when you’re confident
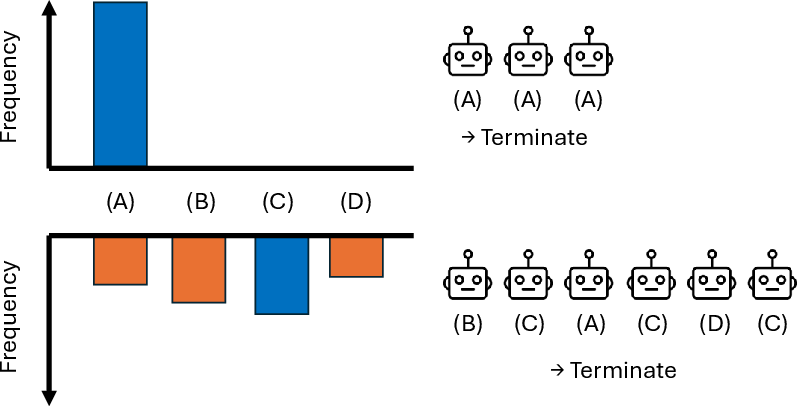
Instead of deciding “I’ll always ask 10 or 100 times,” the paper proposes an adaptive approach:
- Keep sampling answers.
- Track whether one answer seems to be truly the majority.
- Stop early once you have enough evidence that the current majority will likely remain the majority if you kept going.
They measure this “enough evidence” with something called a Bayes factor. Think of it like an “odds meter” that compares:
- Hypothesis H1: “The current top answer really is the majority.”
- Hypothesis H0: “It isn’t.”
When the odds meter passes a chosen threshold, you stop and lock in the majority answer. This saves compute on easy problems (where the majority is clear) and spends more compute only on hard ones.
To handle the fact that the set of possible answers can be unknown or very large (numbers, words, “no answer,” etc.), they use a flexible statistical prior called a Dirichlet process. You can think of it like a smart guesser that:
- Starts open-minded about what answers might appear.
- Updates beliefs as new answers show up.
- Balances “known answers” vs “something new might appear,” controlled by a setting called α (alpha).
3) Mixing multiple LLMs (ensembles) with learned weights
Different LLMs can have different strengths. For example, one might be great at algebra, another at physics, a third at formatting answers properly. The authors combine models by:
- Randomly choosing which model to use on each generation, based on a weight per model (like “listen 40% to Model A, 30% to B, 30% to C”).
- Then doing majority voting over all generated answers.
They find the best weights using a standard optimization tool called a mixed-integer linear program (MILP). In simple terms: it’s a careful, systematic way to pick how much to trust each model so that, across many questions, the combined majority vote is as often correct as possible. The nice part is that this optimization is easier in the “infinite tries” view, and the resulting weights also work well in finite tries with the adaptive stopping rule.
Main findings and why they matter
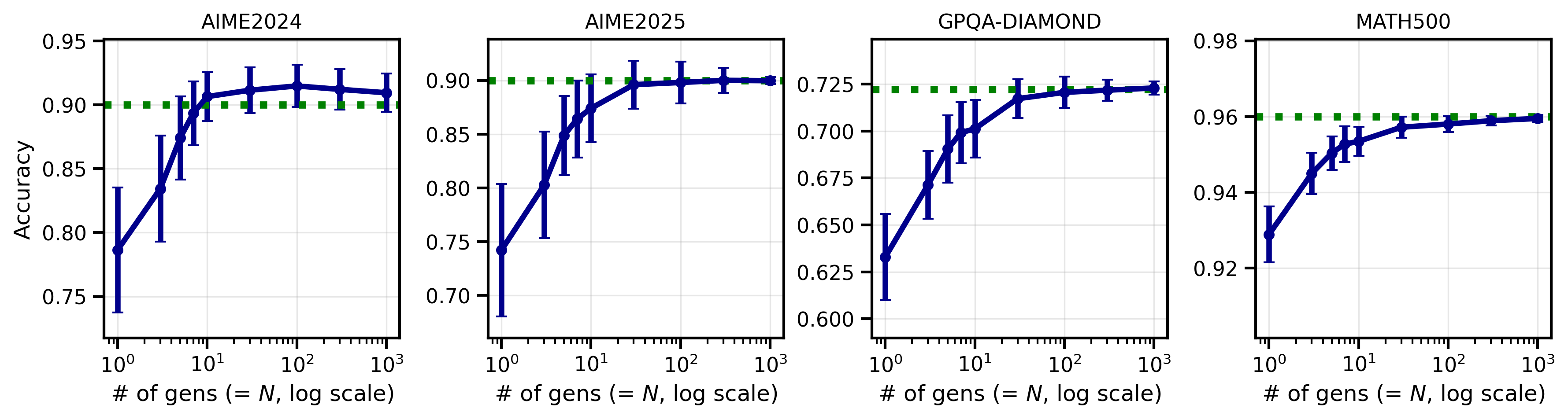
Here are the most important results from their experiments (they tested 11 open-weight LLMs on 4 tough reasoning benchmarks, and generated at least 80 answers per model–question pair, which is much larger than usual):
- Accuracy improves as you ask for more answers (Best-of-N). Even going from around 10 to around 100 samples often helps.
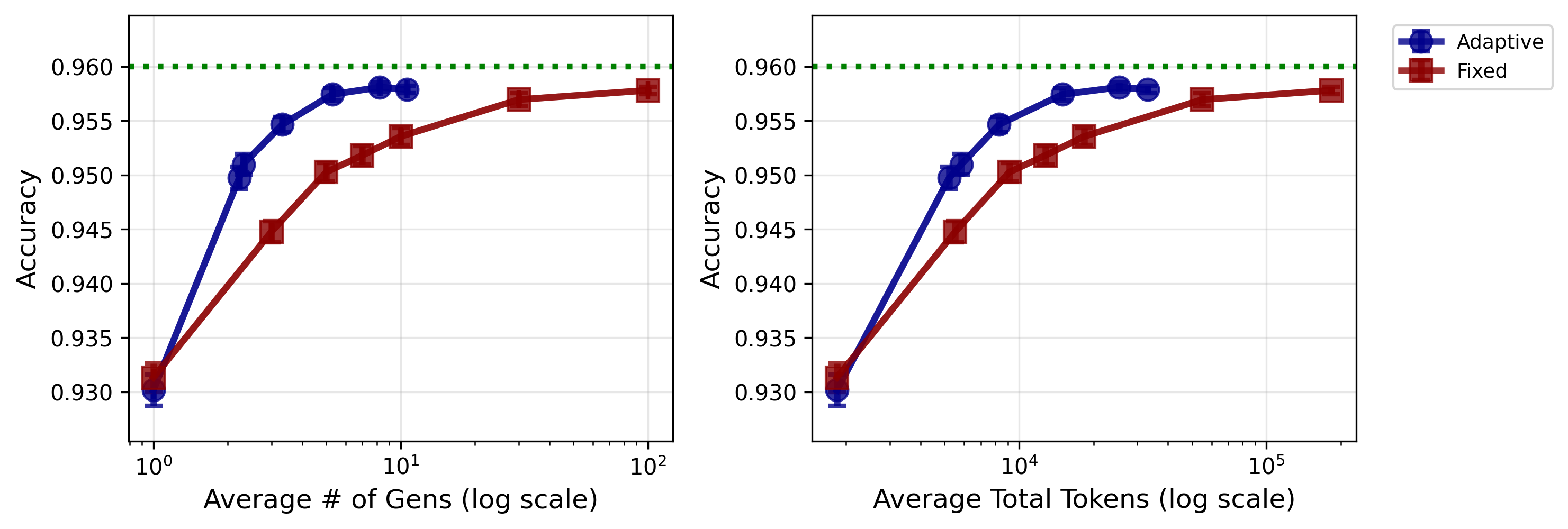
- Adaptive stopping achieves the same accuracy as fixed-N sampling but with far fewer generations:
- On one dataset, their adaptive method with an average of about 3 samples matched the accuracy of always taking 10 samples.
- With about 10 adaptive samples on average, they matched always taking 100 samples.
- This saved roughly 2–5× compute in those tests.
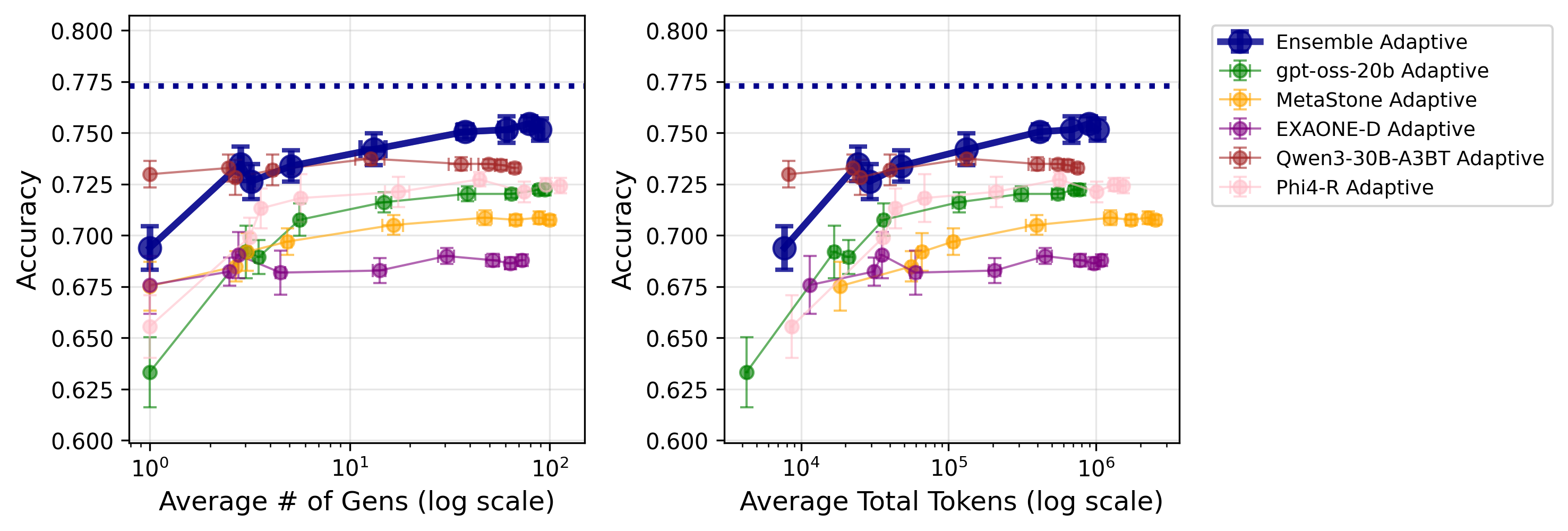
- Model ensembles can beat any single model:
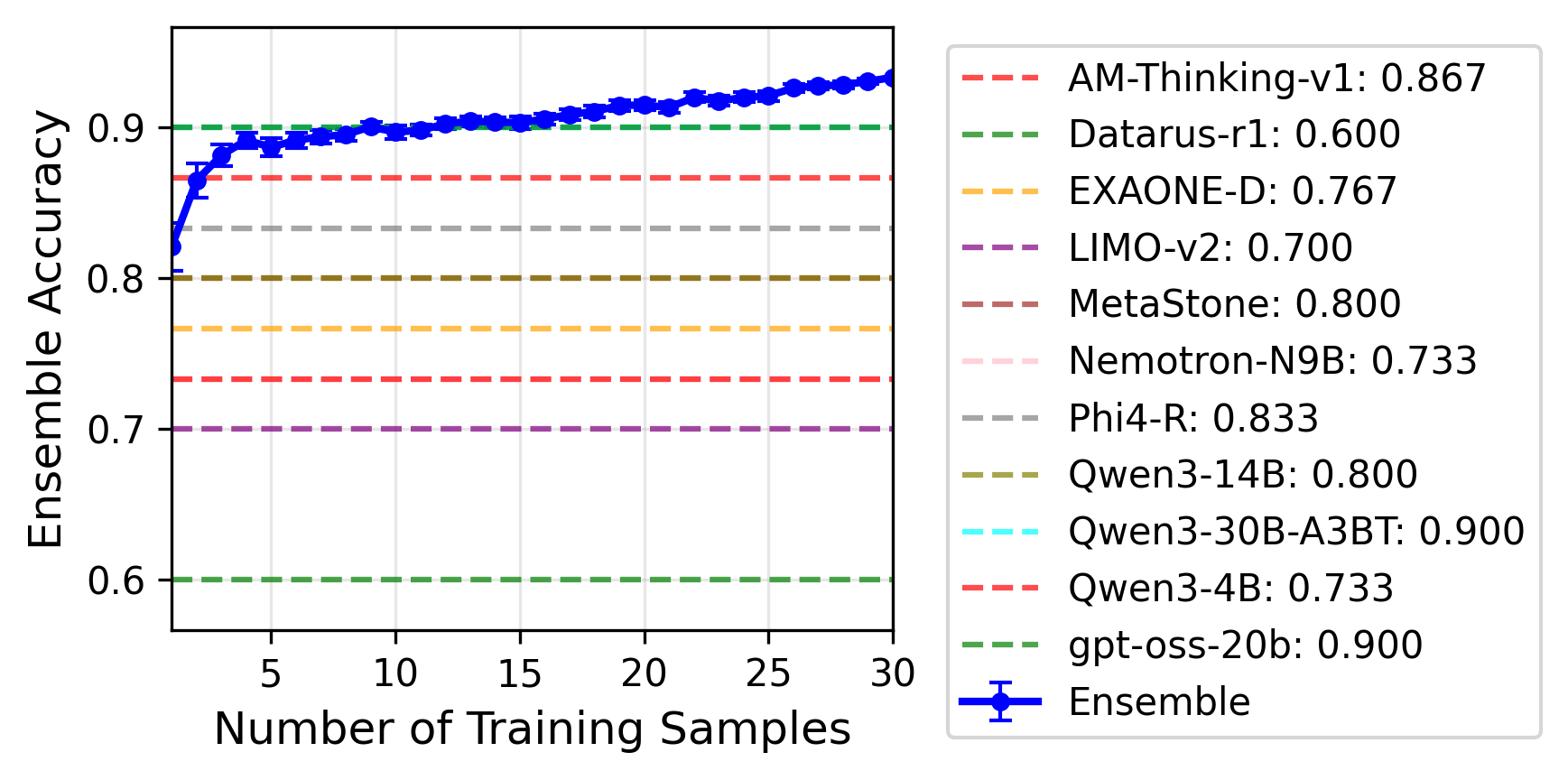
- Example on AIME 2025: one model’s “infinite” majority-vote accuracy was 90.0%, another’s was 73.0%, but their optimized ensemble reached 93.3%.
- This shows that even a “weaker” model can boost the team if it’s good at different things.
- Learning good ensemble weights doesn’t require tons of training questions:
- With only a handful of problems to learn from, the learned weights already approached strong performance; with more, they matched or beat the best single model’s limit.
- Weights often transfer to related tasks (in many tested 3-model combos, weights learned on AIME 2024 matched or beat the best single model on AIME 2025).
- Majority voting is surprisingly strong compared to fancier selection methods:
- In Best-of-5 tests, plain majority voting outperformed random selection, self-reported confidence, several reward models, and “LLM-as-a-judge” methods in their setup—while being simpler and more robust.
What this means (implications)
- Smarter test-time compute: Instead of always spending the same amount of compute per question, stop early when the answer is clear. This can save a lot of time and money while keeping accuracy high.
- Practical path to “near Best-of-∞”: You can get close to the ideal “infinite samples” accuracy without actually taking hundreds of samples every time.
- Stronger together: Mixing multiple LLMs with the right weights can outperform any single model. This lets smaller or differently trained models contribute useful diversity.
- Simple beats complex (sometimes): Majority voting is robust, easy to implement, and can outperform more complicated judging or reward schemes, especially when you increase the number of samples.
- A general recipe for reasoning tasks: For tough problems, it can be better to scale test-time thinking (more tries with smart stopping and ensembling) than to only scale model size.
In short, the paper gives a clear, efficient strategy to boost reliability: ask multiple times, stop when confident, and combine different models wisely.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
The following points summarize what remains unresolved and where further work is needed:
- Finite-sample guarantees are missing: no error-rate or sample-complexity bounds link the Bayes factor threshold B, concentration parameter α, and stopping rule to the probability of selecting the wrong majority or expected number of samples per problem.
- DP-to-Dirichlet approximation is unquantified: the paper approximates the Dirichlet process posterior by a Dirichlet distribution and assumes the base-distribution probability of the current leader () is zero; there are no bounds on the approximation error or guidance on when this is safe.
- Prior ratio approximation is ad hoc: replacing the DP prior with a uniform prior over observed answers in the Bayes factor lacks justification; quantify the impact of this approximation on stopping decisions.
- Assumptions in Theorem 1 are unrealistic for LLMs: consistency requires a finite answer set with non-zero probabilities and ; provide theory for infinite/expanding supports, ties, and heavy-tailed or vanishing probabilities typical of free-form outputs.
- Ties and near-ties are not handled: both the theory and MILP use strict inequalities; propose principled tie-breaking and uncertainty-aware decisions when answer counts are close.
- Independence/stationarity of generations is assumed but untested: assess and model correlation between samples from the same LLM and across LLMs, and quantify its effect on majority voting and stopping rules.
- No calibration of Bayes factor thresholds: provide a mapping from B to desired frequentist error control (e.g., Type I/II errors or e-values) and evaluate anytime validity under the sequential sampling scheme.
- Monte Carlo estimation noise is ignored: the BF is estimated from 1,000 Dirichlet samples; analyze variance-induced decision instability and propose sample-size selection or variance reduction for reliable stopping.
- Hyperparameter α is fixed globally (0.3) without sensitivity analysis: characterize how α impacts stopping, false decisions, and compute cost; propose data-driven or hierarchical methods to adapt α per task/problem.
- Compute-optimality under a global budget is not addressed: develop principled policies to allocate test-time compute across problems (and across LLMs) to maximize accuracy under a fixed token or latency budget.
- Ensemble weights are optimized for only: provide methods to optimize weights for finite (small to moderate), where the asymptotic solution may be suboptimal; include theory and scalable algorithms.
- Max-margin post-processing lacks theory: justify why maximizing margin improves finite- performance; derive bounds or surrogate objectives connecting margin to robustness under sampling noise.
- MILP scalability and reliability are limited: solving up to , is feasible, but scaling to larger model pools or datasets is unaddressed; develop approximations, relaxations, or online/streaming solvers.
- Cost-aware ensembles are not considered: incorporate heterogeneous token costs, latencies, and memory footprints of different LLMs into the objective to trade off accuracy vs. compute.
- Instance-adaptive routing is absent: weights are global and do not use problem features, partial reasoning traces, or self-certainty signals; investigate per-instance model selection or mixture routing that conditions on features.
- Majority-vote failure modes are unexamined: analyze cases where the wrong answer is the modal output (e.g., systematic biases, spurious attractors) and design corrective strategies (verification, minority-checks, confidence-weighted votes).
- Canonicalization and equivalence classes are under-specified: numeric normalization is mentioned, but handling equivalent forms, units, or synonyms (and open-ended answers) is not addressed; extend majority voting beyond strictly categorical outputs.
- Removal of unparseable outputs may bias results: quantify how filtering invalid answers changes the answer distribution and accuracy, and design parsers that minimize bias across models.
- Decoding sensitivity is not studied: report and analyze the impact of temperature, sampling strategy, and prompt formatting on the per-problem answer distributions and on majority-vote behavior.
- Best-of- may not be accuracy-optimal: majority voting in the limit picks the most frequent answer, which can be wrong; explore alternative selection criteria (e.g., verification-guided voting, confidence-weighted schemes) that target correctness rather than frequency.
- Robustness to dataset shift is limited: ensemble weights trained on one benchmark (e.g., AIME2024) partly transfer to another (AIME2025), but no formal generalization guarantees or domain-adaptation methods are provided; develop regularization, robust or distributionally robust optimization.
- Uncertainty in estimated per-problem distributions is ignored: the MILP uses empirical without accounting for estimation error; incorporate confidence intervals or robust formulations to avoid overfitting to finite samples.
- Token-level compute analysis is partial: adaptive sampling reduces samples, but token savings are smaller; provide fine-grained compute models (prompt length, CoT length, stop conditions) and optimize against expected token cost.
- Handling of invalid domain outputs (e.g., “U”) is coarse: treating “U” as always wrong is reasonable, but investigate whether models systematically produce “U” under certain prompts and how ensemble selection affects such failure modes.
- Chain-of-thought (CoT) effects are not analyzed: the paper largely avoids CoT in experiments; evaluate how CoT changes answer distributions, agreement dynamics, stopping behavior, and ensemble benefits.
- Security/adversarial robustness is unaddressed: analyze susceptibility to prompt injection or adversarial inputs that shift the answer distribution to a wrong consensus; propose defenses within the majority-vote framework.
- Practical integration details are missing: standardization across LLM output formats, parsing pipelines, and error handling for multi-model ensembles need clear protocols; quantify their effects on accuracy and compute.
- Broader task coverage is limited: benchmarks focus on math/science QA; evaluate on diverse tasks (code, long-form reasoning, multi-step proofs, multilingual) where answer spaces and agreement dynamics differ.
- Reproducibility and contamination checks need strengthening: provide detailed settings for prompts/decoding, contamination audits for datasets, and cross-run consistency metrics for the large-scale generation corpus.
Practical Applications
Overview
This paper proposes two practical innovations for improving LLM reasoning under compute constraints:
- An adaptive Best-of-N scheme that uses a Bayesian stopping rule (via a Dirichlet process prior and Bayes factor) to decide when sufficient agreement exists to stop generating more answers.
- An optimally weighted ensemble of multiple LLMs for majority voting, where weights are computed via a mixed-integer linear program (MILP) and a max-margin refinement for better finite-N robustness.
Experiments show that:
- Adaptive sampling achieves similar accuracy to fixed Best-of-N with 2–5x fewer generations/tokens.
- Weighted ensembles outperform any single model, even when individual models are weaker but complementary.
- Majority voting often beats reward-model selection or LLM-as-a-judge in answer selection.
Below are the practical applications grouped by deployment horizon, with sectors, tools/workflows, and assumptions noted.
Immediate Applications
- Adaptive majority-voting inference controller for production LLM APIs
- Sectors: software, customer support, search, knowledge management, education, finance
- What: Wrap existing LLM inference with Algorithm 1 (BayesStop), control N via Bayes factor threshold B and concentration α; stop early once consensus is strong; select the most frequent parsed answer.
- Workflow:
- 1) Generate answer samples with temperature > 0 for diversity.
- 2) Maintain answer histograms; compute BF via Monte Carlo from Dirichlet posterior.
- 3) Stop when BF ≥ B or N reaches Nmax; return majority.
- Tools: BayesStop library (DP + BF), token/cost meter, parsing/normalization utilities for discrete answers.
- Impact: 2–5x compute savings at similar accuracy; improved robustness vs reward-model selection.
- Dependencies/Assumptions: Answers must be parseable/normalized; requires randomness in decoding; BF thresholds calibrated per task; minor overhead from Monte Carlo.
- Compute-aware query scheduler that allocates test-time budget adaptively
- Sectors: software platforms, cloud MLops, energy
- What: Allocate more generations only to queries with low agreement; cap compute for high-consensus queries.
- Tools: SLO-aware scheduler, BF-based difficulty estimation, per-tenant budgets.
- Dependencies/Assumptions: Latency SLAs; reliable consensus metrics; monitoring for failure modes when majority is systematically wrong.
- Weighted multi-LLM ensemble for high-stakes reasoning
- Sectors: finance (risk commentary), healthcare (clinical literature synthesis), legal (case analysis), scientific Q&A
- What: Combine several open/closed models; optimize voting weights via MILP on a small in-domain training set; sample per generation using learned w; aggregate via majority.
- Tools: MILP solver (e.g., HiGHS), weight training pipeline, answer schema harmonization, model router implementing random selection according to w.
- Impact: Accuracy above strongest single model; complements specialized capabilities across models.
- Dependencies/Assumptions: Access to multiple LLMs/APIs; licensing/compliance for cross-model use; representative training problems to learn weights; consistent answer formatting.
- Consensus mode for RAG pipelines
- Sectors: enterprise search, BI reporting, compliance
- What: Generate multiple evidence-grounded answers; use adaptive BoN to pick the majority; escalate N only when citations disagree.
- Tools: RAG orchestrator integration; citation consistency checks; BF-based stopping.
- Dependencies/Assumptions: Reliable retrieval; parsing of final structured outputs; guardrails for majority-wrong cases due to retrieval errors.
- VS Code/IDE plugin for consensus code generation and test synthesis
- Sectors: software
- What: Generate multiple code candidates; stop when functions/tests reach majority agreement; present consensus diff.
- Tools: Local wrapper around LLM APIs; BF thresholds; code AST normalization.
- Dependencies/Assumptions: Deterministic formatting/normalization; diversity in generations; unit tests serving as additional verification.
- Cost-efficient benchmarking and evaluation harness
- Sectors: academia, MLops
- What: Replace fixed-N benchmarking with adaptive BoN to standardize accuracy-per-token; use released generation datasets for replication.
- Tools: Open datasets and scripts; BF calculator; reporting of average N, tokens, and accuracy.
- Dependencies/Assumptions: Benchmarks with discrete outputs; consistent parsing rules; reproducible random seeds.
- Majority voting as a drop-in alternative to reward-model selection
- Sectors: software, education, scientific Q&A
- What: Avoid reward hacking and overfitting when scaling N; use majority vote for selection in BoN instead of reward models or LLM-as-a-judge.
- Tools: Simple answer frequency counter; tie-breaking policy; logging.
- Dependencies/Assumptions: Applicability strongest when correct answers dominate with higher probability than incorrect ones; tie handling.
- Adaptive crowd-labeling and QA workflows
- Sectors: data annotation, research
- What: Request more labels only when BF indicates insufficient consensus; stop early otherwise.
- Tools: DP prior over categories; BF-based stopping; label aggregator.
- Dependencies/Assumptions: Categorical labels; platform integration; annotator variability analogous to model variability.
Long-Term Applications
- Continual ensemble weight learning and deployment at scale
- Sectors: software platforms, finance, healthcare, government
- What: Periodically retrain MILP weights on rolling in-domain datasets; add max-margin refinement; monitor drift and retrain.
- Tools: AutoML pipeline for MILP weight optimization; drift detection; A/B testing to validate weight updates.
- Dependencies/Assumptions: Stable distributions or robust retraining cadence; enough labeled tasks to avoid overfitting; solver scalability.
- Cross-model consensus standards and interoperability
- Sectors: software, policy
- What: Standardize answer schemas (final numeric/string outputs, multiple-choice letters) and confidence/metadata so majority voting works across vendors.
- Tools: Schema specs; normalization libraries; compliance certifications.
- Dependencies/Assumptions: Vendor cooperation; handling free-form text via post-processing into discrete form; governance for licensing.
- Risk-tiered compute policies for public-sector and safety-critical use
- Sectors: healthcare, finance, government
- What: Define BF thresholds and Nmax by risk tier; enforce multi-model ensembles for high-risk decisions; audit consensus and explainability logs.
- Tools: Policy templates; compliance reporting; energy/compute accounting.
- Dependencies/Assumptions: Human-in-the-loop requirements; clear disclaimers; regulatory acceptance; robust monitoring for majority-wrong cases.
- Edge and robotics decision-making with adaptive sampling
- Sectors: robotics, IoT
- What: Use lightweight local models in ensemble; escalate compute only when low consensus; defer to cloud for hard cases.
- Tools: On-device schedulers; BF estimation under tight latency; model diversity on edge.
- Dependencies/Assumptions: Real-time constraints; small models with complementary strengths; safe fallbacks.
- Hybrid model–human ensembles with expertise weighting
- Sectors: healthcare, legal, scientific review
- What: Extend weighted voting to include human experts using Dawid–Skene-like estimators of annotator expertise; optimize weights jointly.
- Tools: Expertise estimation; MILP/convex formulations; audit trails.
- Dependencies/Assumptions: Availability of expert feedback; privacy/ethics; careful calibration to avoid overreliance on majority.
- Verification-enhanced consensus for math and structured tasks
- Sectors: education, engineering
- What: Combine majority voting with external verifiers (e.g., symbolic solvers, unit-checkers) to filter consensus answers that fail verification.
- Tools: Math solvers; static analyzers; checker APIs.
- Dependencies/Assumptions: Availability of verifiers; integration overhead; risk of rejecting correct answers due to verifier limitations.
- Energy/sustainability frameworks for inference-time scaling
- Sectors: energy, policy, cloud providers
- What: Standardize reporting of tokens, average N, and BF thresholds; optimize for accuracy-per-kWh; publish sustainability metrics.
- Tools: Metering; dashboards; procurement criteria.
- Dependencies/Assumptions: Accurate energy measurement; willingness to adopt standards; trade-offs with latency and accuracy.
- Educational platforms with adaptive compute for personalized learning
- Sectors: education
- What: Tutors escalate compute only on harder student problems (low-consensus responses); ensembles provide robust answers and explanations.
- Tools: Difficulty estimation via BF; content alignment; parental/teacher controls.
- Dependencies/Assumptions: Age-appropriate guardrails; structured answer formats; privacy compliance.
- Consensus-as-a-Service APIs
- Sectors: software vendors, integrators
- What: Offer turnkey endpoints implementing adaptive BoN and ensemble weighting; configurable α, B, Nmax; logging and observability.
- Tools: Managed solvers; caching; versioned weight profiles per domain.
- Dependencies/Assumptions: SLA guarantees; cost models; model supply (open and closed).
Glossary
- Adaptive sampling: An on-the-fly procedure that adjusts the number of generations based on observed agreement to decide when to stop sampling. "An illustration of adaptive sampling (Algorithm \ref{alg:adaptive_sampling})."
- Base distribution: The prior distribution over the (possibly infinite) answer space in a Dirichlet process that governs the probability of new, unseen answers. "Here, H is a base distribution over the answer space, and α > 0 is a concentration parameter that controls the likelihood of generating new answers."
- Bayes factor: A likelihood ratio that quantifies how much the observed data support one hypothesis over another. "Confidence in the majority is based on the Bayes factor."
- Bayes factor threshold: A preset cutoff on the Bayes factor used to decide when to stop sampling and accept the majority. "Maximum samples , concentration parameter , Bayes factor threshold ."
- Bayes' theorem: A rule relating priors, likelihoods, and posteriors, used here to express the Bayes factor in terms of posterior odds and prior odds. "(Bayes' theorem)"
- Best-of-N (BoN): An inference-time strategy that generates N candidate answers and selects one via a criterion such as majority vote. "A simple yet effective strategy is the best-of- (BoN) approach, where we generate answers and select the best one based on some criteria."
- Best-of-one (Bo1): The special case of BoN where only a single generation is used, often serving as a baseline. "we first consider the best-of-one (Bo1) policy"
- **Best-of-∞ (best-of-N \to \infty."
- Concentration parameter: In a Dirichlet process, a positive scalar controlling how likely new, unseen answers are to appear. " is a concentration parameter that controls the likelihood of generating new answers."
- Conjugate distribution: A prior distribution family that yields posteriors in the same family after observing data; used here for the categorical via the Dirichlet. "The Dirichlet distribution is a conjugate distribution of the categorical distribution of of answers, where the last dimension corresponds to the unobserved answers."
- Dirichlet distribution: A multivariate distribution over categorical probabilities, used as a posterior approximation for answer frequencies. "The Dirichlet distribution is a conjugate distribution of the categorical distribution of of answers, where the last dimension corresponds to the unobserved answers."
- Dirichlet process (DP): A nonparametric Bayesian prior over distributions that flexibly models an unknown, potentially unbounded set of answer categories. "we adopt a Dirichlet process prior over the answer space"
- Ensemble majority voting: Aggregating outputs from multiple models and selecting the most frequent answer across them. "Importantly, ensemble majority voting can naturally benefit from complementarity."
- Gold answer: The ground-truth answer against which predictions are evaluated. "For each problem, let be the gold answer."
- Half-space: A linear inequality-defined region in space; intersections of half-spaces characterize polytopes used in the optimization. "The region of \eqref{ineq_nbest} is an intersection of the following half-spaces:"
- LLM-as-a-judge: A selection paradigm where an LLM evaluates and picks among candidate answers instead of majority voting. "LLM-as-a-judge (tournament)"
- LLM ensemble: A mixture of multiple LLMs combined via sampling or weighting to improve robustness and accuracy. "Second, we investigate the advantage of LLM ensemble over single LLM."
- Majority voting: Selecting the answer that appears most frequently among multiple generations. "Another approach is majority voting \citep{wang2023selfconsistency} in which the most frequent answer is selected."
- Marginal likelihood (evidence): The probability of the observed data under a hypothesis, integrating over parameters; used in the Bayes factor. "Here, are the evidence (marginal likelihood) based on the observed data."
- Max margin: Choosing an ensemble weight solution with the largest safety margin from decision boundaries to improve finite-N robustness. "we adopt a ``max margin'' solution"
- Mixed-integer linear program (MILP): An optimization problem with linear constraints/objective and both integer and continuous variables, used to learn ensemble weights. "The optimal ensemble weighting is formulated and efficiently computed as a mixed-integer linear program."
- Monte Carlo methods: Random sampling techniques used to approximate integrals or probabilities, such as posterior probabilities under a Dirichlet. "it can be estimated using Monte Carlo methods by sampling from the Dirichlet distribution."
- Non-concavity: A property of an objective function that prevents guarantees from gradient-based optimization due to multiple local optima. " is a non-concave function on the simplex space of ."
- Nonparametric Bayesian modeling: Bayesian approaches that do not fix the number of parameters a priori, allowing flexible model complexity. "a particularly well-suited approach is to employ nonparametric Bayesian modeling."
- NP-hard: A complexity class indicating that a problem is at least as hard as the hardest problems in NP; exact MILP solving falls here. "General MILP solving is NP-hard;"
- Polyhedron: A geometric object defined as the intersection of finitely many half-spaces (linear inequalities). "which is a polyhedron."
- Polytope: A bounded polyhedron; here, regions in weight space where a particular answer is the majority form polytopes. "Then, the following set, which implies that answer is the most frequent answer, is a polytope:"
- Posterior: The updated probability distribution after observing data, combining prior beliefs and likelihood. "Then, the posterior distribution is"
- Reward hacking: Exploiting flaws in a reward model to achieve higher scores without genuinely better answers. "majority voting is robust to reward hacking and benefits from additional generations with minimal risk"
- Reward model: A learned model that scores candidate answers to pick the best one. "One common approach is to use a reward model to select the best answer"
- Self-certainty: A selection heuristic based on a model’s own reported confidence in its outputs. "Self-certainty"
- Simplex: The set of nonnegative weight vectors that sum to one; the feasible region for ensemble weights. "Visualization of the non-concave objective function over the weight simplex ."
- Uniform prior: A prior that assigns equal probability mass across considered categories or hypotheses. "(approximating the prior ratio by uniform prior)"
- Weighted majority vote: Majority voting where each model’s vote is scaled by a predefined weight vector. "our design choice is to take a weighted majority vote with ."
Collections
Sign up for free to add this paper to one or more collections.