An Iteration-Free Fixed-Point Estimator for Diffusion Inversion

Abstract: Diffusion inversion aims to recover the initial noise corresponding to a given image such that this noise can reconstruct the original image through the denoising diffusion process. The key component of diffusion inversion is to minimize errors at each inversion step, thereby mitigating cumulative inaccuracies. Recently, fixed-point iteration has emerged as a widely adopted approach to minimize reconstruction errors at each inversion step. However, it suffers from high computational costs due to its iterative nature and the complexity of hyperparameter selection. To address these issues, we propose an iteration-free fixed-point estimator for diffusion inversion. First, we derive an explicit expression of the fixed point from an ideal inversion step. Unfortunately, it inherently contains an unknown data prediction error. Building upon this, we introduce the error approximation, which uses the calculable error from the previous inversion step to approximate the unknown error at the current inversion step. This yields a calculable, approximate expression for the fixed point, which is an unbiased estimator characterized by low variance, as shown by our theoretical analysis. We evaluate reconstruction performance on two text-image datasets, NOCAPS and MS-COCO. Compared to DDIM inversion and other inversion methods based on the fixed-point iteration, our method achieves consistent and superior performance in reconstruction tasks without additional iterations or training.

• The paper introduces an iteration-free fixed-point estimator that decouples neural network error for precise diffusion inversion.
• It leverages a localized temporal approximation to reduce model evaluations from 140–150 to just 50 per image, improving LPIPS, SSIM, and PSNR.
• The approach minimizes variance and preserves high-frequency details, simplifying hyperparameter tuning and advancing practical image editing.

Iteration-Free Fixed-Point Estimation for Efficient Diffusion Model Inversion

Introduction and Motivation

Diffusion inversion—the process of recovering the initial noise vector for a given image in a denoising diffusion probabilistic model (DDPM) trajectory—has become foundational for enabling content-preserving image manipulation, prompt-based editing, style transfer, and preference-optimizing workflows in diffusion models. Existing methods, such as DDIM inversion, suffer from error accumulation due to latent approximation at each step, while fixed-point iteration-based approaches significantly increase computational cost and require sensitive tuning of iteration counts. The paper "An Iteration-Free Fixed-Point Estimator for Diffusion Inversion" (2512.08547) addresses these limitations by formulating and analyzing a non-iterative, statistically grounded estimator for diffusion inversion, yielding state-of-the-art reconstruction quality with minimal compute.

Figure 1: Overview of inversion methods—ideal step (unknown latent), DDIM inversion (precedes with approximation, accumulates error), fixed-point iterative methods (require multiple iterations), and the proposed iteration-free estimator (single unbiased estimation per step).

Technical Approach

The core contribution is a closed-form expression for the fixed point of the inversion step, explicitly separating the neural network prediction error from the solution. Building on this, the method leverages a localized temporal approximation: the data prediction error at step $t_i$ is approximated by its previous-step value, $e_{t_{i-1}}$, which is directly computable. This forms a practical, unbiased, and low-variance estimator for the unknown latent at each time step of inversion. The algorithm proceeds as follows:

1. Start from the ground-truth image, using an explicit formula to initialize the estimate for the first inversion step (where no prior error is known).
2. At each subsequent step, use the error from the preceding step in the closed-form inversion equation.
3. At every stage, only one forward pass through the neural network is required—no inner-loop iterations are performed.
4. Theoretical analysis confirms the estimator is unbiased relative to the fixed-point solution and exhibits lower error variance than variants omitting error approximation.

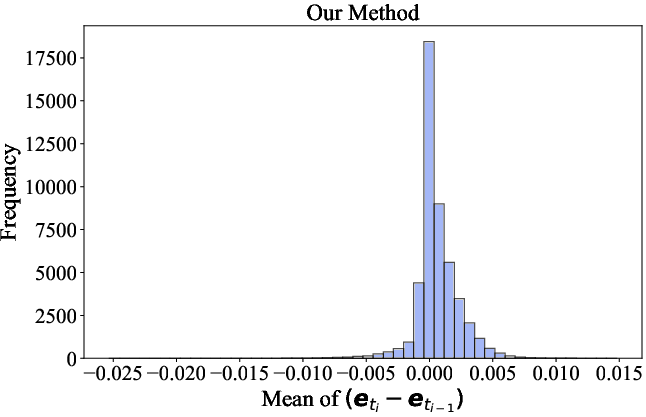
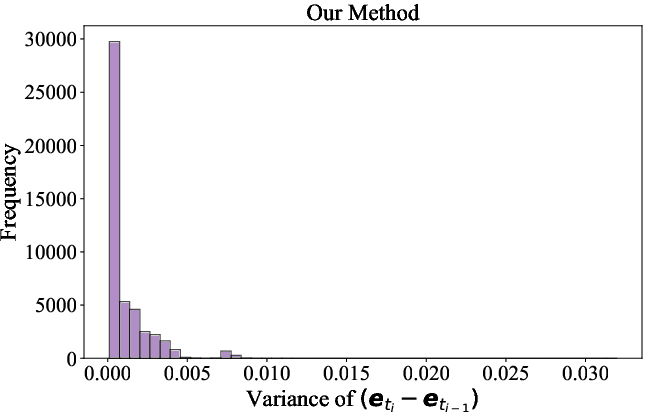
Figure 2: Statistical analysis substantiates unbiased fixed-point estimation (a) and low variance (b) for the error-approximating estimator.

Experimental Evaluation

Extensive experiments on MS-COCO 2017 and NOCAPS benchmarks, with both Stable Diffusion v1.4 and SDXL, evaluate the estimator across PSNR, LPIPS, SSIM, and CLIP-I metrics. The proposed Iteration-Free Fixed-Point Estimator (IFE) is compared to DDIM inversion, ReNoise, AIDI, and EasyInv.

Key results:

• On MS-COCO, IFE achieves LPIPS of 0.216 (best), SSIM of 0.733, and PSNR of 31.66 with only 50 total model evaluations, outperforming all baselines—including state-of-the-art fixed-point iteration-based methods, which require 140–150 evaluations per image.
• On NOCAPS with SDXL, IFE delivers an LPIPS of 0.205, SSIM of 0.849, and PSNR of 33.48, again matching or exceeding the editability and fidelity of multi-iteration competitors but with significantly lower compute.
• Empirical ablation studies demonstrate that omitting the error approximation catastrophically degrades performance (LPIPS increases to 0.277); thus, the approximation is essential for high-quality inversion.
• Qualitative comparisons reveal IFE robustly preserves structure and high-frequency detail, while DDIM and fixed-point methods often introduce artifacts or lose fidelity when constrained to a reasonable compute budget.

  Figure 3: Qualitative comparison on NOCAPS—IFE preserves fine facial structure, avoids over-saturation, and mitigates artifacts that afflict DDIM inversion, AIDI, ReNoise, and EasyInv.

Further comparisons against various numbers of fixed-point iterations confirm that IFE matches or exceeds “optimal” multi-iteration performance, sidestepping the non-monotonicity and instability endemic to tuning iteration counts in those baselines.

Figure 4: Visual comparison—IFE achieves consistent, optimal reconstructions across diverse images, while the baseline’s necessary iterations are image-dependent and error-prone.

Theoretical Implications

The theoretical findings highlight several notable points:

• The iteration-free estimator is a provably unbiased estimator (zero-mean error distribution) for the inversion fixed point under the local error distribution model adopted from ADM-ES.
• Its variance is minimized by leveraging temporal correlation of the network’s data prediction error across adjacent steps. Empirically, this yields lower MSE than both DDIM inversion and the variant without error approximation.
• The estimator’s independence from iterative refinement allows for stable, deterministic inversion trajectories and greatly simplifies hyperparameter selection.

Practical Implications and Future Directions

This method’s practical relevance is significant for workflows relying on large-scale image inversion: style transfer, object manipulation, content editing, and preference optimization are immediately accelerated and unlocked for deployment in limited-resource or latency-sensitive contexts. Since the estimator is training-free and model-agnostic, the approach generalizes across existing and future diffusion-model architectures.

The main limiting assumption is the local smoothness of the prediction error; future work may address adaptation to highly stochastic samplers or non-DDIM variants, and extend to other modalities (e.g., video or 3D scenes) where temporal or spatial error dynamics differ. Improved modeling of error dynamics and exploitation of cross-step dependencies may enable even higher fidelity or further computation reduction.

Conclusion

This work presents a theoretically principled and empirically validated solution to the costly iteration bottleneck of fixed-point diffusion inversion methods. By explicitly modeling local error and exploiting stepwise error approximation, the authors’ estimator delivers best-in-class reconstruction accuracy with a single evaluation per step, obviating iterative search and tuning. The approach sets a new technical standard for diffusion inversion efficiency and opens new avenues for computation-aware downstream application in image generation and editing (2512.08547).