Group Representational Position Encoding (2512.07805v1)

Abstract: We present GRAPE (Group RepresentAtional Position Encoding), a unified framework for positional encoding based on group actions. GRAPE brings together two families of mechanisms: (i) multiplicative rotations (Multiplicative GRAPE) in $\mathrm{SO}(d)$ and (ii) additive logit biases (Additive GRAPE) arising from unipotent actions in the general linear group $\mathrm{GL}$. In Multiplicative GRAPE, a position $n \in \mathbb{Z}$ (or $t \in \mathbb{R}$) acts as $\mathbf{G}(n)=\exp(n\,ω\,\mathbf{L})$ with a rank-2 skew generator $\mathbf{L} \in \mathbb{R}^{d \times d}$, yielding a relative, compositional, norm-preserving map with a closed-form matrix exponential. RoPE is recovered exactly when the $d/2$ planes are the canonical coordinate pairs with log-uniform spectrum. Learned commuting subspaces and compact non-commuting mixtures strictly extend this geometry to capture cross-subspace feature coupling at $O(d)$ and $O(r d)$ cost per head, respectively. In Additive GRAPE, additive logits arise as rank-1 (or low-rank) unipotent actions, recovering ALiBi and the Forgetting Transformer (FoX) as exact special cases while preserving an exact relative law and streaming cacheability. Altogether, GRAPE supplies a principled design space for positional geometry in long-context models, subsuming RoPE and ALiBi as special cases. Project Page: https://github.com/model-architectures/GRAPE.

• The paper introduces the GRAPE framework, unifying multiplicative rotations from SO(d) and additive logit biases to improve positional encoding.
• It presents closed-form expressions that enable efficient computation and precise capture of relative positional information.
• Experimental results demonstrate that GRAPE outperforms methods like RoPE, offering enhanced training stability and improved long-context performance.

Abstract

The paper introduces the Group Representational Position Encoding (GRAPE) framework, a unified approach to positional encoding for sequence modeling. GRAPE combines two mechanisms: multiplicative rotations, termed Multiplicative GRAPE, and additive logit biases, termed Additive GRAPE. Multiplicative GRAPE employs rotations in the special orthogonal group $\SO(d)$, while Additive GRAPE arises from unipotent actions in the general linear group $\mathrm{GL}(d)$. GRAPE captures the essential geometric properties required for positional encoding in long-context models, extending the capabilities of previously established methods like Rotary Position Embedding (RoPE) and ALiBi.

Introduction

Positional information is crucial in the transformer architecture, addressing the limitation of permutation-invariant self-attention mechanisms. Classical approaches injected absolute positional codes, while subsequent innovations embraced relative encodings and linear biases, optimizing length extrapolation without computational overhead. RoPE exemplifies relative positional encoding through orthogonal rotations that are norm-preserving and origin invariant. GRAPE aims to unify these approaches, providing a comprehensive framework that encapsulates both multiplicative and additive mechanisms.

GRAPE Framework

Multiplicative GRAPE

Multiplicative GRAPE models positional encodings through rotations in $\SO(d)$, specifically using rank-2 skew generators. This approach preserves norms and supports efficient computation via closed-form matrix exponentials.

Implementation Details: Positions are encoded as: $\Gb(n) = \exp(n \omega \Lb) \in \SO(d)$ with $\Lb$ being a skew-symmetric generator defined by vectors $\ab$ and $\bbb$.

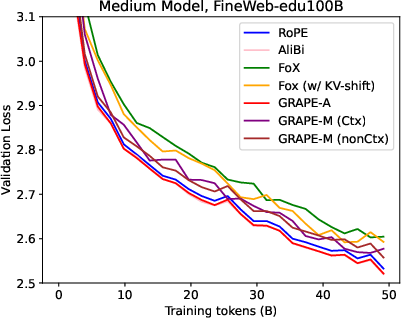
Figure 1: Training Loss

Additive GRAPE

Additive GRAPE employs unipotent actions within $\mathrm{GL}(d)$ to achieve additive logit biases, supporting streaming cacheability and preserving relative scoring.

Implementation Details: The additive positional encoding is realized through: $\Gb_{\text{add}}(n) = \exp(n \omega \Ab)$ resulting in low-rank transformations that introduce linear-in-offset biases.

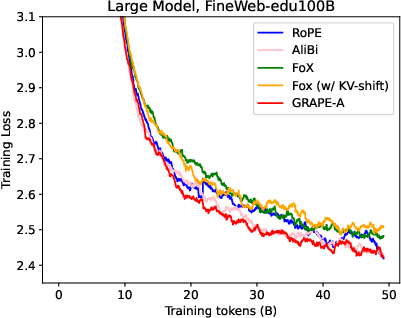
Figure 2: Training Loss

Contributions

1. Unified Framework: GRAPE offers a group-theoretic unification of positional encodings, enabling comprehensive extensions.
2. Closed-form Expressions: Derivation of closed-form matrix exponentials for efficient computation in multiplicative GRAPE.
3. Exact Logit Projection: Implementation of rank-1 unipotent actions to capture ALiBi and Forgetting Transformer extensions precisely.
4. Experimental Analysis: Demonstrates GRAPE's persistent edge over existing methods, including RoPE and FoX, in both training stability and performance.

Conclusion

GRAPE provides a principled design space for positional encoding mechanisms, enhancing the capabilities of transformer architectures in long-context scenarios. By subsuming existing approaches under a unified framework, GRAPE facilitates further research and development of efficient, scalable models.

The implications of this work extend across both practical and theoretical domains, promising advancements in AI's ability to model complex sequences with intricate positional requirements. Future research may explore adaptive, context-sensitive frequency modulation and its integration into the broader GRAPE framework.