Symmetries at the origin of hierarchical emergence (2512.00984v1)

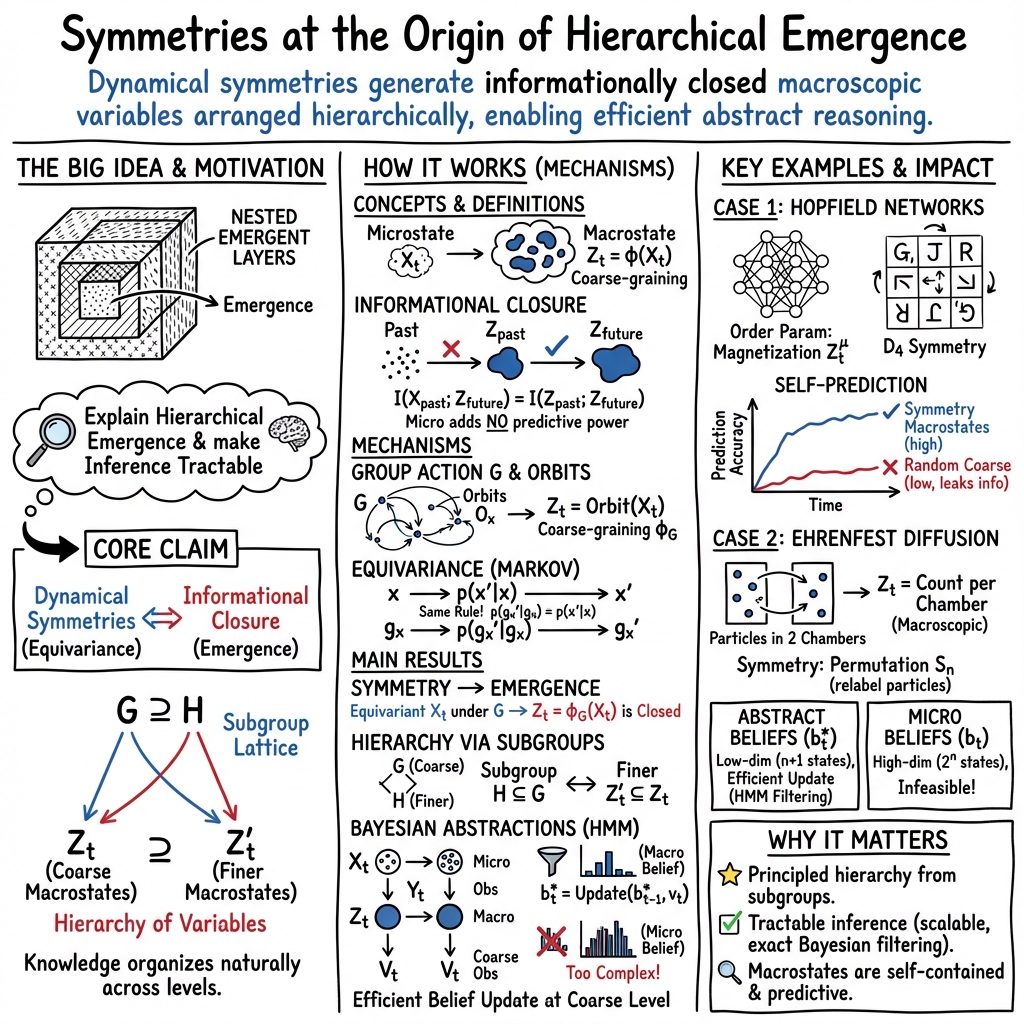
Abstract: Many systems of interest exhibit nested emergent layers with their own rules and regularities, and our knowledge about them seems naturally organised around these levels. This paper proposes that this type of hierarchical emergence arises as a result of underlying symmetries. By combining principles from information theory, group theory, and statistical mechanics, one finds that dynamical processes that are equivariant with respect to a symmetry group give rise to emergent macroscopic levels organised into a hierarchy determined by the subgroups of the symmetry. The same symmetries happen to also shape Bayesian beliefs, yielding hierarchies of abstract belief states that can be updated autonomously at different levels of resolution. These results are illustrated in Hopfield networks and Ehrenfest diffusion, showing that familiar macroscopic quantities emerge naturally from their symmetries. Together, these results suggest that symmetries provide a fundamental mechanism for emergence and support a structural correspondence between objective and epistemic processes, making feasible inferential problems that would otherwise be computationally intractable.

• The paper demonstrates that dynamical symmetry induces informationally closed macrostates via subgroup lattices, enabling efficient hierarchical inference.
• It integrates group theory, information theory, and statistical mechanics with analytical and numerical results to validate emergent order parameters.
• Applications in Hopfield networks and Ehrenfest diffusion illustrate significant computational gains by leveraging symmetry-driven coarse-graining.

Symmetry as the Driver of Hierarchical Emergence

Introduction

The paper "Symmetries at the origin of hierarchical emergence" (2512.00984) establishes a formal connection between symmetry and the origin of hierarchical emergent structures in dynamical systems. Integrating group theory, information theory, and statistical mechanics, the work demonstrates that equivariance of system dynamics under a symmetry group $G$ produces a nested hierarchy of informationally closed macroscopic variables. These macroscopic variables, organized according to the subgroup lattice of $G$, not only encapsulate all the dynamically relevant information but also yield tractable Bayesian inference procedures at multiple levels. The theoretical claims are elucidated via analytical and numerical investigations in Hopfield networks and the Ehrenfest diffusion model, demonstrating automatic emergence of natural order parameters encoding relevant macroscopic phenomena.

Symmetry, Informational Closure, and Hierarchical Organization

The foundational concept is informational closure: a macroscopic variable $Z_t$ is emergent if knowledge of its history suffices to predict its future, and conditioning on the underlying microstate $X_t$ provides no additional predictive power. This property is quantified via mutual information,

$$I({X}_{t}; {Z}_{t+1}^{L}) - I({Z}_{t}; {Z}_{t+1}^{L}) = 0$$

for all block lengths $L$. The central claim is that if dynamics are equivariant under a group $G$, meaning transition kernels are invariant under group actions ($p(g x_{t+1}|g x_t) = p(x_{t+1}|x_t)$ for all $g\in G$), then coarse-graining the state space by the orbits of $G$ yields informationally closed levels. Moreover, the subgroup lattice of $G$ induces a hierarchy: coarser macrostates correspond to larger subgroups, and finer ones to smaller subgroups, yielding a partial ordering that mirrors the algebraic structure.

Figure 1: Symmetry-induced Markov chain dynamics over six states and the D$_3$ subgroup lattice structuring informationally closed coarse-grainings.

The implications are substantial: symmetry provides not just a mechanism for universality in physics, but a general principle for the emergence of nested macrostates in arbitrary finite dynamical systems.

Application to Hopfield Networks

The theory is made concrete in Hopfield networks, which serve as canonical models for associative memory. The paper formalizes that the Mattis magnetization—dot products between candidate patterns and the network state—are precisely the informationally closed macroscopic variables when the pattern set exhibits equivariance under permutations.

By constructing groups generated by permutations or additional symmetries such as the dihedral group $D_4$, the Markovian dynamics of the Hopfield network exhibit equivariance, leading to emergent coarse-grained variables tracking letter identity, rotational/reflection properties, or combinations thereof.

Figure 2: Hopfield network symmetries induce coarse-grained order parameters, with numerical results confirming superior predictive power of symmetry-derived coarse-grainings.

Strong numerical results demonstrate that coarse-grainings derived from symmetry clearly outperform arbitrary ones of the same cardinality in predictive self-containment, quantifying the claim that symmetry-derived macrostates capture all dynamically relevant information.

Hierarchies of Bayesian Inference Under Symmetry

The same algebraic framework is extended to epistemic processes—Bayesian inference over partially observed systems. In the setting of equivariant hidden Markov models (HMMs), the measurement model and latent process both respect the symmetry group, enabling the construction of abstract belief states at emergent levels. These belief states form their own HMMs, allowing exact Bayesian updates at variable resolutions and radically reducing computational complexity.

Figure 3: Equivariant dynamical symmetries structure the hierarchy of Bayesian updates on macroscopic scales, with different levels corresponding directly to subgroup coarse-grainings of the process.

A commutative diagram formalizes the compatibility between belief updates at various scales—a marginalization at the micro-scale corresponds precisely to coarse-scale belief updates under certain information closure conditions.

Figure 4: Commutative structure underpins consistency between marginalization and Bayesian belief updates at different levels.

Ehrenfest Diffusion as a Concrete Example

Ehrenfest's model—a paradigmatic statistical mechanics instance—is analyzed to illustrate the tractability gains afforded by symmetry-induced abstraction. Permutation symmetry among particles leads to macrostates characterized by particle counts per chamber. Standard microstate beliefs scale exponentially ($2^n$), whereas abstract beliefs grow linearly ($n+1$), leading to orders-of-magnitude computational gains in Bayesian inference.

Figure 5: Emergence of abstract beliefs about particle counts in Ehrenfest diffusion, with exponential savings over microstate inference as system size increases.

The same hierarchical organization via the subgroup lattice of $S_n$ induces a nested set of tractable, coarse-grained inference problems, extending the formalism to intermediate macroscopic levels as well.

Theoretical and Practical Impact

The paper makes several bold and technically substantive claims:

• Symmetry-induced coarse-grainings guarantee informational closure, establishing a formal existence result for hierarchical emergent variables.
• Hierarchy in the subgroup lattice directly translates into a nested, partial ordering of macrostates and abstract belief states, providing an algebraic blueprint for emergent organization.
• Bayesian inference on macrostates is not only exact but computationally tractable if measurements themselves respect underlying symmetries.

On the theoretical front, these results unify notions of emergence from information theory, group theory, and statistical mechanics, providing concrete formal and numerical tools to study emergence beyond thermodynamic limits and far from criticality. In the practical domain, the approach offers a constructive recipe for reducing complex inference problems in high-dimensional systems to tractable forms, via symmetry analysis and group-theoretic coarse-graining.

Implications and Future Directions for AI

Symmetry-driven abstraction opens novel perspectives for AI, particularly in hierarchical modeling, efficient inference, and representation learning. The presented formalism suggests principled approaches for identifying emergent features or abstract states in arbitrary dynamical environments, critical for scalable reasoning in POMDPs and reinforcement learning. There is considerable promise for integrating group-theoretic abstraction with geometric deep learning architectures to facilitate symmetry-aware learning and inference [bronstein2021geometric].

Extending the methodology to weak or approximate symmetry scenarios, leveraging graph-coloring and symmetry fibration techniques, could further enhance its applicability in real-world, noisy systems (cf. [makse2025symmetries]). Additionally, combining symmetry-induced abstraction with variational inference and renormalization group-inspired latent modeling delineates a rich and tractable design space for next-generation artificial agents and scientific inference engines.

Conclusion

This work establishes symmetry, specifically dynamical equivariance, as a necessary and sufficient structural principle for hierarchical emergence and efficient multilevel inference in stochastic dynamical systems. The subgroup lattice of the underlying symmetry group formalizes the organization of macrostates and belief hierarchies, and practical gains in inference tractability are validated. The implications span both foundational theory and practical methodology, offering a rigorous basis for abstraction and hierarchical modeling across physics, cognitive science, and artificial intelligence.