Parameter Symmetry Potentially Unifies Deep Learning Theory (2502.05300v2)

Abstract: The dynamics of learning in modern large AI systems is hierarchical, often characterized by abrupt, qualitative shifts akin to phase transitions observed in physical systems. While these phenomena hold promise for uncovering the mechanisms behind neural networks and LLMs, existing theories remain fragmented, addressing specific cases. In this position paper, we advocate for the crucial role of the research direction of parameter symmetries in unifying these fragmented theories. This position is founded on a centralizing hypothesis for this direction: parameter symmetry breaking and restoration are the unifying mechanisms underlying the hierarchical learning behavior of AI models. We synthesize prior observations and theories to argue that this direction of research could lead to a unified understanding of three distinct hierarchies in neural networks: learning dynamics, model complexity, and representation formation. By connecting these hierarchies, our position paper elevates symmetry -- a cornerstone of theoretical physics -- to become a potential fundamental principle in modern AI.

• The paper introduces parameter symmetry as a unifying principle for deep learning phenomena, reducing model complexity and aligning learning dynamics.
• It details how symmetry-to-symmetry transitions during training correlate with saddle point escapes and regularization effects in gradient descent.
• The study highlights that harnessing symmetry can lead to universally aligned, low-complexity representations, guiding new neural network designs.

Parameter Symmetry Potentially Unifies Deep Learning Theory

Introduction

The paper "Parameter Symmetry Potentially Unifies Deep Learning Theory" (2502.05300) posits an intriguing hypothesis: parameter symmetry breaking and restoration is a mechanism capable of unifying several observed phenomena within deep learning. These phenomena, universal across various architectures and datasets, have traditionally been explained through fragmented theories focusing on specific models. This paper proposes a holistic view, suggesting that parameter symmetry serves as a foundational principle influencing learning dynamics, model complexity, and representation formation.

Parameter Symmetry in Deep Learning

Parameter symmetry is defined as a property of models wherein transformations applied to model parameters result in unchanged outputs. Such symmetries are prevalent in neural network architectures and can significantly restrict the hypothesis space of potential solutions, inherently shaping the learning process. Understanding these symmetries can offer insights into the constraints and efficiencies of neural network training processes.

Figure 1: The division of solution space into hierarchies given by distinct parameter symmetries.

Learning Dynamics and Symmetry

The paper introduces the concept of symmetry-to-symmetry learning dynamics. Neural networks exhibit dynamics characterized by transitions between symmetry states. These transitions coincide with sudden leaps in model complexity and learning milestones, often observed as saddle point escapes. Symmetry creates extended saddle points that are challenging for gradient descent algorithms to navigate, hence affecting the convergence properties and learning trajectories.

Figure 2: DNN learning dynamics is symmetry-to-symmetry.

Model Complexity Reduction via Symmetry

Parameter symmetry can reduce the effective complexity of models by imposing constraints on the space of possible solutions. When symmetry is present, neural networks tend to converge toward solutions that exhibit lower complexity, aligning with the target function's complexity. Symmetry acts akin to Occam’s Razor, favoring simpler solutions, which explains why the generalization errors in overparameterized networks do not grow with model width.

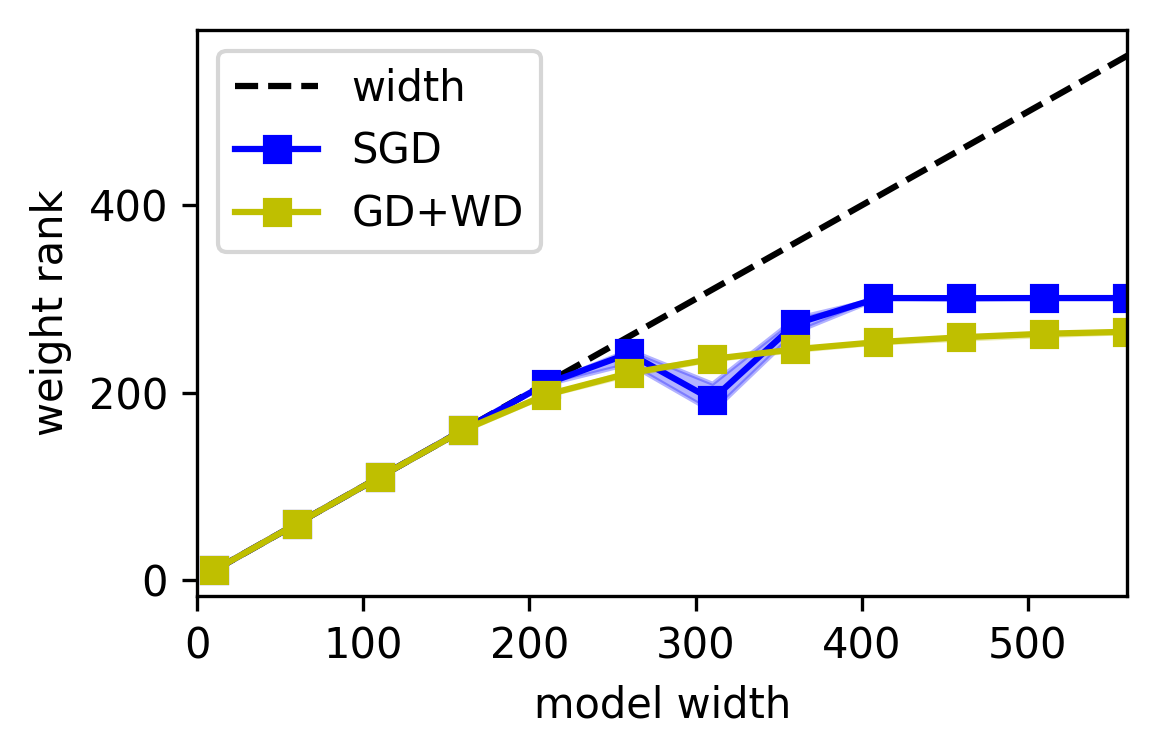
Figure 3: The complexity and generalization error of neural networks do not grow with width.

Representation Learning: Necessity of Symmetry

Representation formation in neural networks, known for its hierarchical nature, is significantly influenced by parameter symmetry. Symmetries can naturally lead to the formation of structured, invariant representations like neural collapse, where intra-class variations are reduced. Symmetry ensures a lower rank in the learned representations, facilitating hierarchical encoding of information.

Figure 4: Neural collapse (NC) only happens when permutation symmetry is present.

Universality and Alignment in Representations

The paper discusses the phenomenon of universal representation alignment across different trained models. It demonstrates how symmetries can lead different models, trained independently, to converge toward similar, universally aligned representations. This universality extends even to biological counterparts of artificial networks.

Figure 5: Universally aligned representations emerge in differently trained neural networks.

Mechanisms and Control

The paper elaborates on mechanisms behind symmetry breaking and restoration, highlighting regularization and stochastic gradient descent (SGD) as significant factors. Regularization biases solutions towards symmetric states, while SGD induces implicit regularization effects. The possibility of controlling symmetry through model design offers avenues for deliberately engineering hierarchical learning dynamics within AI systems.

Conclusion

The paper offers compelling evidence that parameter symmetry is an integral principle unifying diverse learning phenomena within deep learning. It proposes that symmetry can be harnessed in model design to control hierarchical learning attributes like dynamics, complexity, and representation structure. This perspective aligns AI research closer to principles known in physics, suggesting promising interdisciplinary paths. Future research can explore these symmetry dynamics further, potentially revolutionizing approaches to understanding and designing AI systems.