Uncertainty Quantification for Visual Object Pose Estimation
Abstract: Quantifying the uncertainty of an object's pose estimate is essential for robust control and planning. Although pose estimation is a well-studied robotics problem, attaching statistically rigorous uncertainty is not well understood without strict distributional assumptions. We develop distribution-free pose uncertainty bounds about a given pose estimate in the monocular setting. Our pose uncertainty only requires high probability noise bounds on pixel detections of 2D semantic keypoints on a known object. This noise model induces an implicit, non-convex set of pose uncertainty constraints. Our key contribution is SLUE (S-Lemma Uncertainty Estimation), a convex program to reduce this set to a single ellipsoidal uncertainty bound that is guaranteed to contain the true object pose with high probability. SLUE solves a relaxation of the minimum volume bounding ellipsoid problem inspired by the celebrated S-lemma. It requires no initial guess of the bound's shape or size and is guaranteed to contain the true object pose with high probability. For tighter uncertainty bounds at the same confidence, we extend SLUE to a sum-of-squares relaxation hierarchy which is guaranteed to converge to the minimum volume ellipsoidal uncertainty bound for a given set of keypoint constraints. We show this pose uncertainty bound can easily be projected to independent translation and axis-angle orientation bounds. We evaluate SLUE on two pose estimation datasets and a real-world drone tracking scenario. Compared to prior work, SLUE generates substantially smaller translation bounds and competitive orientation bounds. We release code at https://github.com/MIT-SPARK/PoseUncertaintySets.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
Robots often need to figure out where an object is and how it’s turned (this is called its “pose”) just by looking at a single camera image. But that estimate is never perfect. This paper shows how to draw a smart, tight “safety bubble” around a pose estimate that almost surely contains the object’s true pose. The key is that this bubble:
- comes with statistical guarantees (so it’s trustworthy),
- doesn’t assume any specific noise shape (it’s “distribution-free”),
- and adapts its shape to the problem instead of being a simple sphere.
The authors call their method SLUE, which stands for S-Lemma Uncertainty Ellipsoid.
What questions are the authors trying to answer?
Here are the main goals, stated simply:
- How can we convert uncertainty in 2D image points (like detected corners on an object) into a reliable 3D uncertainty around the object’s pose?
- Can we create an uncertainty “bubble” whose shape adjusts to the situation (instead of assuming a round sphere) so it’s as small as possible while still being safe?
- Can we split this joint pose uncertainty into separate, easy-to-understand pieces: “how unsure are we about position?” and “how unsure are we about orientation?”
- Will this work well and fast on real datasets and real robots?
How does the method work? (Plain-language overview)
Think of taking a photo of an object. A neural network marks important points on the object in the image (called “keypoints”). But each marked point has some error. The paper’s method does this:
- Step 1: Get trustworthy 2D keypoint uncertainty.
- For each keypoint, they build a small square region around the detected pixel location that, say, 90% of the time contains the true pixel. They get this from a technique called conformal prediction. You can think of it as “calibrating” the size of the square so the promised confidence level is true on average.
- Step 2: Turn 2D uncertainty into 3D pose rules.
- Each pixel square backprojects into a cone-shaped region in 3D space where that point could be. Combining these cones for several keypoints, plus the object’s 3D model and the camera’s geometry, creates a bunch of rules that the true pose must satisfy. This set of all allowed poses is messy and can be non-convex (think: bumpy and irregular).
- Step 3: Wrap it with the smallest safe ellipsoid (a squashed 3D “balloon”).
- Instead of dealing with the messy shape directly, the method finds a single ellipsoid (centered at the current pose estimate) that covers all poses that obey the rules. Importantly, it chooses the ellipsoid with the smallest volume that still safely contains everything. This makes the uncertainty both compact and easy to use.
- To do this efficiently and with guarantees, they use a math tool called the S-lemma. Intuitively, the S-lemma is a rule that lets you replace many complicated constraints with one “combined” constraint that’s still safe. The first version is fast but a bit conservative.
- Step 4: Tighten the bubble if you want.
- They add a “hierarchy” using sum-of-squares (SOS) polynomials. You can think of this as turning up the dial to do more detailed checking. As you increase the level, the ellipsoid gets tighter and approaches the true smallest possible ellipsoid. Higher levels take more computation but give smaller uncertainty.
- Step 5: Split pose uncertainty into position and orientation.
- From the joint ellipsoid, they project out two simpler bounds:
- a position ellipsoid (how uncertain the object’s location is),
- and an orientation bound (how uncertain the object’s rotation is), expressed in an intuitive “axis–angle” way (a direction to twist and an amount of twist).
Throughout, the method is “distribution-free”: it doesn’t assume the noise is, say, Gaussian. It only needs reliable bounds on keypoint errors, which conformal prediction provides.
What did they find, and why does it matter?
Here are the main takeaways from tests on two popular pose datasets and a real drone-tracking scenario:
- Smaller, smarter uncertainty bubbles for position:
- Compared to earlier methods that fixed the bubble’s shape (like forcing it to be a sphere), SLUE makes the shape fit the data. This usually means much smaller position uncertainty regions, especially along the camera’s viewing direction where single-camera vision is naturally more uncertain (the “scale ambiguity” problem).
- Competitive orientation bounds:
- Their orientation uncertainty is similar in quality to the best previous methods, while keeping strong guarantees.
- Trustworthy and flexible:
- The method provides high-probability coverage without needing to assume a particular noise distribution. It also works with any pose estimator you already have; it just adds reliable uncertainty on top.
- Fast and tunable:
- The first-level version is the fastest among bounding approaches they compare to, and you can tighten the bounds further with the SOS hierarchy if you have extra compute time.
Why it matters: Robots need to be cautious when they’re unsure (e.g., move slower near a possibly misplaced obstacle) and can be more confident when uncertainty is small. SLUE gives a principled, compact, and guaranteed way to measure that uncertainty, helping robots make safer and better decisions.
What’s the impact and what could come next?
- Safer planning and control:
- Autonomous cars, drones, and robot arms can use these uncertainty bounds to plan safer paths—slowing down or giving more space when uncertainty is large, and moving efficiently when it’s small.
- Easy to plug in:
- SLUE can sit on top of existing pose-estimation pipelines. It only needs 2D keypoint detections, the camera’s intrinsics, and the object’s 3D model.
- Robust in the real world:
- Because it’s distribution-free, it can better handle real-world noise that doesn’t follow neat textbook patterns.
- Future directions:
- Extending to handle object symmetries (when different rotations look the same), multiple cameras, or moving/ deformable objects would make it even more powerful.
In short, this paper provides a practical, mathematically grounded way to wrap pose estimates with tight, trustworthy uncertainty—exactly the kind of information robots need to act safely and confidently.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored, focusing on aspects future researchers could address.
- Dependence among keypoint errors and joint coverage: The paper’s coverage guarantee for the joint pose constraint set relies on independence or a union bound across per-keypoint conformal sets, which can yield low overall coverage. Develop multivariate or structured conformal methods that calibrate a single joint uncertainty set over all keypoints to achieve a specified global coverage level under dependence.
- Choice and calibration of keypoint uncertainty sets: The method assumes split conformal prediction yields valid per-keypoint bounds under exchangeability. Investigate robustness to domain shift, dataset shift, and non-exchangeable residuals; design online or domain-adaptive calibration schemes for keypoint uncertainty that maintain target coverage in changing environments.
- Handling occlusions and missing keypoints: The derivation assumes each annotated 3D keypoint has a detectable, visible pixel measurement with a valid uncertainty set. Extend SLUE to partial, missing, or occluded keypoint sets (including visibility inference), and quantify the impact on coverage and bound tightness.
- Norm choice and anisotropy: The paper favors infinity-norm pixel error bounds for computational benefits. Explore anisotropic (elliptical) pixel uncertainty sets, per-keypoint covariance-aware bounds, or heteroscedastic models, and quantify trade-offs in tightness, runtime, and coverage versus using L∞ bounds.
- Ellipsoid center selection: The bounding ellipsoid is constrained to be centered at a given pose estimate, which may be biased or far from the feasible set. Study optimizing the center (e.g., Chebyshev center or other certified centers) jointly with shape for smaller, more informative bounds without sacrificing guarantees.
- Conservatism and volume suboptimality: The generalized S-lemma/SOS relaxations are outer bounds that may be conservative at low orders. Provide theoretical and empirical characterizations of the conservatism (e.g., bound on volume ratio to the true minimum-volume ellipsoid), and criteria predicting when low-order relaxations suffice.
- Scaling and higher-order relaxations: The paper uses relaxation orders up to κ=1 for tractability. Investigate scalability to higher κ with many keypoints, large object sets, or real-time settings, including exploiting sparsity, chordal decompositions, or first-order methods to reduce computational burden.
- Rotation representation and projection tightness: Angular bounds are obtained via axis-angle projection with θ≤90° or via quaternions (appendix). Quantify the tightness loss from projecting the joint ellipsoid to rotation-space metrics; compare axis-angle, quaternion, and geodesic (SO(3)) projections and develop tighter rotation-only bounds.
- Object symmetries: The approach does not capture symmetry-induced pose ambiguity. Incorporate symmetry groups and equivalence classes into the constraint set and uncertainty bounds (e.g., quotient spaces), enabling certified orientation bounds consistent with symmetric objects.
- Monocular-only assumptions: SLUE is designed for monocular sensing and captures scale ambiguity but not multi-view constraints. Extend to multi-view or temporal settings to reduce ambiguity and improve tightness; derive certified fusion of bounds across frames/views.
- Camera model assumptions: The formulation assumes known pinhole intrinsics and ignores lens distortion or intrinsics uncertainty. Extend SLUE to handle uncertain or estimated intrinsics (and distortion), and quantify how camera parameter uncertainty propagates into pose bounds.
- Robustness to outliers and misdetections: Conformal sets provide high-probability bounds, but gross keypoint errors (e.g., spurious detections) can break guarantees. Integrate robust estimation (e.g., certified outlier rejection, RANSAC-like screening with guarantees) into SLUE, and analyze failure modes.
- Visibility and chirality constraints near degeneracies: The FoC constraint requires positive depth; near-zero depth or grazing angles can degrade numerical stability. Characterize these degeneracies and develop stabilized constraints or regularization for near-singular configurations.
- Category-level and unknown-instance objects: The method assumes known CAD keypoints for specific instances. Generalize to category-level tracking with shape/pose uncertainty, learned keypoint priors, or deformable models, and propagate shape uncertainty into certified pose bounds.
- End-to-end integration with pose estimators: Although SLUE is estimator-agnostic, the center and bound quality depend on the pose estimate. Investigate end-to-end training or estimator designs that explicitly minimize bound volume or improve SLUE tightness while retaining statistical guarantees.
- Translation–rotation coupling: The joint ellipsoid is projected into separate translation and rotation bounds; this may discard useful coupling. Explore certified downstream controllers/planners that directly consume the joint ellipsoid, or develop coupled bounds that remain interpretable.
- Computational guarantees and solver behavior: The paper reports practical stability of log-det objectives with MOSEK/TSSOS despite prior reports of difficulties. Provide formal conditions or diagnostics for numerical stability and convergence; benchmark alternative solvers and parameterizations.
- Coverage–tightness trade-offs: Empirically, SLUE yields smaller translation bounds and competitive orientation bounds, but the paper does not fully map the trade-off between confidence level, keypoint set size, relaxation order, and bound volume. Systematically characterize these trade-offs to guide parameter selection.
- Dynamic tracking and online updates: The approach is evaluated on static frames and specific datasets. Develop online SLUE variants for tracking with temporal smoothness priors, incremental updates, and certified time-varying bounds suited for real-time robotics.
- Non-keypoint features: SLUE operates on semantic keypoints. Explore extending to dense features, contours, or learned geometric primitives, and derive corresponding uncertainty constraints and bounding procedures with guarantees.
Practical Applications
Immediate Applications
Below are concrete, deployable use cases that leverage the paper’s SLUE method and findings for distribution-free, statistically rigorous pose uncertainty in monocular vision.
- Healthcare (lab automation) — Certified grasp and placement with monocular cameras:
- Use SLUE’s ellipsoidal bounds to select safe grasps and placements for vials, well plates, or instruments when using low-cost monocular cameras in benchtop robots. If the translational bound around an object overlaps forbidden zones (e.g., other samples), trigger re-sensing or slower approach profiles.
- Tools/workflow: Existing keypoint-based pose estimators + split conformal calibration for keypoint uncertainty + SLUE-1 (first-order) for fast bounds; integrate into ROS MoveIt to inflate collision geometry with SLUE ellipsoids.
- Assumptions/dependencies: Known CAD model and annotated keypoints; calibrated intrinsics; reasonable keypoint detector accuracy; conformal calibration data representative of deployment; solver availability (e.g., MOSEK); object symmetry not captured by SLUE.
- Robotics (industrial manipulation, warehouse automation) — Uncertainty-aware pick-and-place:
- Inflate grasp approach and alignment tolerances using SLUE’s translation and axis-angle bounds; route uncertain items to “verification lanes” or multi-view re-checks, and adjust suction cup vs. parallel-jaw gripper selection based on bound shape (e.g., long axis indicates depth uncertainty).
- Tools/workflow: SLUE joint ellipsoid + translation projection (Ht) and orientation projection (Hθ) computed per pick; plug into robust MPC or grasp synthesis (e.g., GraspIt!, Dex-Net) as deterministic constraints.
- Assumptions/dependencies: Object models available; camera intrinsics calibrated; keypoint nets trained and conformally calibrated; computational budget acceptable for per-pick bound updates; axis-angle projection assumes θ ≤ 90° (or use quaternion variant).
- Autonomous driving and mobile robotics — Safe navigation around uncertain obstacles:
- Use SLUE bounds to inflate dynamic obstacles detected via monocular perception (traffic cones, debris, pedestrians with wearable markers), modulating speed and clearance based on certified pose uncertainty volume.
- Tools/workflow: Navigation stack (Nav2/Autoware) consumes SLUE ellipsoids as obstacle inflation; planner switches to conservative trajectories when log-det(H) exceeds threshold; conformal pixel bounds from keypoint detectors (e.g., Mask R-CNN keypoints).
- Assumptions/dependencies: Reliable keypoint detection and conformal calibration for target classes; monocular scale ambiguity handled via SLUE shape optimization but may remain conservative; coverage depends on correlation among keypoint errors.
- UAVs/drones — Collision avoidance and tracking with certified keep-out zones:
- In drone-to-drone or drone-to-object tracking (as in the paper’s CAST scenario), use SLUE translation bounds to define keep-out volumes and trigger evasive maneuvers when predicted trajectories intersect uncertainty ellipsoids.
- Tools/workflow: Integrate SLUE-1 for real-time bounds; broadcast uncertainty metadata in MAVLink messages; flight controller (PX4/ArduPilot) uses bounds to adjust safety margins.
- Assumptions/dependencies: Onboard compute for SDP/SOS solving or offloading to ground station; calibrated camera; known target geometry; keypoint detections with conformal uncertainty.
- Quality assurance and safety engineering — “Uncertainty budgets” for perception:
- Replace ad-hoc pose confidence heuristics with SLUE’s distribution-free bounds in test plans and safety cases; define acceptance criteria (e.g., maximum allowable ellipsoid volume or max axis-angle radius) for release gates.
- Tools/workflow: Regression dashboards log SLUE volumes across datasets (LM-O, YCB-V, CAST); thresholding policies in CI/CD; automated re-training when coverage falls below target.
- Assumptions/dependencies: Representative calibration set for conformal prediction; domain drift monitoring; solver stability; agreed-upon coverage metrics for multi-keypoint dependence.
- AR/VR and consumer software — Confidence-aware object placement:
- Show a “confidence bubble” (SLUE ellipsoid) around virtual objects in monocular AR apps, adapt rendering (e.g., occlusion or shadow strength) and user prompts when pose uncertainty grows.
- Tools/workflow: Mobile keypoint detectors + lightweight SLUE-1; UI overlays with ellipsoid; degrade features or request user re-scan on large bounds.
- Assumptions/dependencies: Mobile-friendly solver or precomputed approximation of SLUE; known 3D models; sufficient calibration data for conformal bounds; latency constraints.
- Academia (research and teaching) — Robust perception and optimization curriculum:
- Use the released code to teach conformal prediction, S-lemma, and SOS relaxations; benchmark students’ pose pipelines with guaranteed uncertainty bounds; explore trade-offs between SLUE-1 and SLUE-κ.
- Tools/workflow: Course modules on distribution-free UQ; TSSOS and MOSEK labs; assignments on LM-O/YCB-V with empirical coverage analysis.
- Assumptions/dependencies: Access to solvers; datasets with CAD and keypoints; compute resources for SOS hierarchy experiments.
Long-Term Applications
Below are use cases that become practical with further research, scaling, and engineering, including extensions hinted by the paper (SOS hierarchy, quaternion variants) and ecosystem needs (standards, hardware acceleration).
- Standards and certification (policy, transportation, aviation) — Regulatory-grade uncertainty reporting:
- Establish SLUE-like, distribution-free pose uncertainty as a requirement in safety cases for AVs and UAVs; regulators (e.g., NHTSA, FAA, ISO 26262/18497) accept bounded ellipsoids with documented coverage as evidence in hazard analyses.
- Tools/products: “Certified UQ module” audited library; conformance test suites measuring empirical coverage under dependence; reporting schemas for uncertainty telemetry.
- Assumptions/dependencies: Consensus on dependence modeling across keypoints; standardized datasets and procedures for conformal calibration; domain shift monitoring; legal and standards bodies’ buy-in.
- Robotics (advanced manipulation) — Symmetry-aware and multi-object certified perception:
- Extend SLUE to capture object symmetries and multi-hypothesis orientation (integrate orientation distributions from EPOS-like methods); jointly bound multiple objects with interaction constraints for cluttered scenes.
- Tools/products: SLUE-κ with symmetry priors; multi-object SDP formulations; grasp planners consuming multi-hypothesis bounds.
- Assumptions/dependencies: New theory for symmetry-aware outer bounds; scalable solvers; richer priors and models.
- Multimodal fusion (software, robotics) — Certifiable sensor fusion with monocular, depth, and LiDAR:
- Combine SLUE’s monocular bounds with conformal or distribution-free bounds from other modalities to create tighter joint uncertainty sets for pose and scene geometry.
- Tools/workflow: Fusion layer that intersects/fuses ellipsoids or zonotopes; robust MPC using fused sets; calibration pipelines per modality.
- Assumptions/dependencies: Cross-modal calibration; fusion rules preserving guarantees; compute overhead; synchronized sensing.
- End-to-end learning (ML for perception) — Differentiable SLUE and bound-aware training:
- Make SLUE differentiable to train keypoint networks that minimize bound volume directly (e.g., log-det loss), promoting detectors that are inherently uncertainty-efficient while remaining distribution-free at inference.
- Tools/products: SLUE layer in PyTorch/JAX; curriculum learning with bound penalties; deployment with split conformal recalibration.
- Assumptions/dependencies: Stable gradients through SDP/SOS layers; surrogate losses aligning with true bound volume; training data breadth; compute cost.
- Real-time embedded deployment (software/hardware) — Acceleration and approximation of SOS hierarchy:
- Develop specialized solvers or hardware acceleration (FPGA/GPU) for SLUE-κ to achieve low-millisecond latency, enabling per-frame bounds in high-speed robotics.
- Tools/products: Approximate SLUE (e.g., warm-started SDP, preconditioned first-order methods); hardware IP cores for SOS/SDP primitives.
- Assumptions/dependencies: Solver research; hardware design; power and thermal budgets; approximation error controls preserving outer-bound guarantees.
- Healthcare (surgical robots) — Certified monocular tracking for tool and anatomy localization:
- Use SLUE bounds to ensure safe tool approach and avoid critical structures when vision-only tracking is employed (e.g., MIS settings); provide interpretable uncertainty overlays to surgeons.
- Tools/workflow: Clinical-grade perception stack with SLUE; HMI for uncertainty visualization; fail-safe policies based on bound size.
- Assumptions/dependencies: Extensive clinical validation; regulatory approval; robust keypoint detection in challenging visuals (specularities, occlusions); known models or patient-specific preoperative models.
- AR/VR (platforms) — OS-level uncertainty services:
- Offer an OS/runtime service that exposes certified pose uncertainty to apps, enabling consistent safety-aware rendering and interactions across the ecosystem.
- Tools/products: Platform APIs exposing ellipsoids and coverage; developer guidelines; background calibration services.
- Assumptions/dependencies: Standardized model repositories; privacy-preserving calibration; mobile solver stacks.
- Education and benchmarking (academia, industry consortia) — Coverage-driven benchmarks and datasets:
- Create benchmarks where success is measured by both accuracy and certified coverage under domain shift, encouraging robust, distribution-free perception methods.
- Tools/workflow: New datasets with controlled dependence among keypoints; leaderboards scoring empirical coverage, bound tightness, and runtime.
- Assumptions/dependencies: Community adoption; sustained dataset curation; compute resources for broad evaluation.
Notes on feasibility across applications:
- SLUE’s guarantees rely on high-probability pixel keypoint uncertainty sets from conformal prediction. Calibration data must be exchangeable with deployment data; domain shift reduces empirical coverage.
- Coverage for the joint pose set depends on dependence among keypoint errors. Independence yields lower theoretical coverage; positive correlation increases it. In practice, monitor empirical coverage and adjust α or recalibrate.
- Monocular scale ambiguity is reflected in bound shape (often elongated along optical axis); planners must interpret anisotropy correctly.
- Axis-angle projection assumes θ ≤ 90°; use the quaternion variant to avoid this limitation when needed.
- The method does not inherently resolve pose ambiguity from object symmetries; orientation bounds may be conservative for symmetric objects.
- Solver availability and runtime matter. First-order SLUE-1 is fast and conservative; SLUE-κ tightens bounds at higher compute cost. For real-time, consider warm starts, approximations, or hardware acceleration.
Glossary
- Axis-angle: A rotation representation defined by an axis of rotation and the angle around it; often used to describe small rotational deviations. "axis-angle orientation bounds."
- Backprojection constraint: A constraint that enforces consistency between 2D pixel measurements and their feasible 3D points when backprojected through camera geometry. "To proceed we convert the rational reprojection constraint~\eqref{eq:yminusgt} to a polynomial backprojection constraint."
- Chirality (front-of-camera) constraint: A constraint ensuring that 3D points being projected are in front of the camera (positive depth), not behind it. "This is the chirality (front-of-camera) constraint for keypoint :"
- Conformal prediction: A distribution-free statistical framework that provides uncertainty sets with guaranteed coverage under minimal assumptions. "obtained with, e.g., conformal prediction"
- Duality gap: The difference between the optimal values of a primal optimization problem and its dual; a nonzero gap indicates the relaxation may be conservative. "at the cost of a possible duality gap."
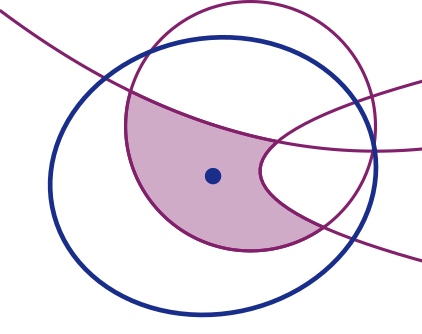
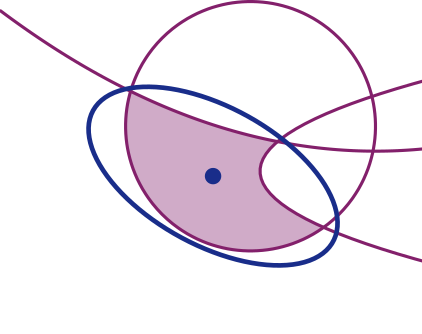
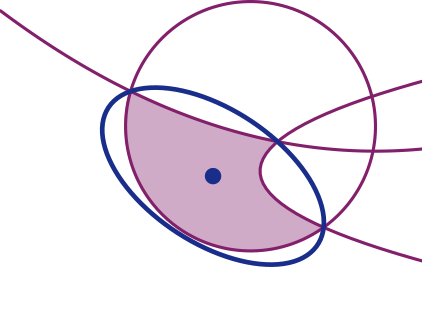
- Ellipsoidal outer bound: An ellipsoid that contains a target set, serving as a simple geometric over-approximation of a possibly non-convex set. "using an ellipsoidal outer bound."
- Generalized S-Lemma: An extension of the classical S-lemma that provides sufficient conditions to certify one quadratic inequality from others, possibly with multiple constraints. "a generalization of the classical S-lemma"
- Homogeneous form: A coordinate representation where points are expressed with an extra scale component, enabling projective transformations. "in homogeneous form ()."
- Homogenized variable: An augmented variable that includes a constant component to convert affine or rational constraints into polynomial or quadratic form. "in the homogenized variable $\*x \triangleq [1, \*r^T, \*t^T]^T$"
- Infinity-norm: A vector norm equal to the maximum absolute value among the vector’s components, often leading to axis-aligned box constraints. "bounded in infinity-norm with high probability"
- Kronecker identity: An identity relating matrix products to Kronecker products and vectorization, useful for rewriting bilinear forms. "we use the Kronecker identity: $\*M\*R\*b_i = (\*b_i^T \otimes \*M)\*r$"
- Kronecker product: A matrix operation producing a block matrix that captures tensor-like products of matrices. "We denote the Kronecker product with "
- Löwner-John ellipsoid problem: The problem of finding the minimum-volume ellipsoid that contains a given convex set. "known as the Löwner-John ellipsoid problem"
- Log determinant objective: An optimization objective using the logarithm of the determinant of a positive definite matrix, often proportional to ellipsoid volume. "The log determinant objective, which gives minimum volume, is dismissed as impractical."
- Minimum volume bounding ellipsoid: The smallest-volume ellipsoid that encloses a given set, used for compact outer approximations. "relaxation of the minimum volume bounding ellipsoid problem"
- Monomial basis: A structured set of monomials up to a given degree used to parameterize polynomials in SOS programming. "we denote the -order monomial basis in variable $\*x\in\mathbb{R}^n$ by $[\*x]_\kappa\in\mathbb{R}^{C(n + \kappa - 1, \kappa)}$"
- Orthogonal projection: A linear projection onto a subspace that preserves perpendicularity, used here to project joint ellipsoids onto translation-only bounds. "via orthogonal projection"
- Perspective-n-point: A classic computer vision problem and solver for estimating a camera pose from 3D-2D point correspondences. "We use standard perspective-n-point~\cite{Terzakis20eccv-sqpnp} to generate a pose estimate"
- Pose uncertainty constraint set: The set of 6D poses satisfying measurement-based constraints that, with high probability, contains the true pose. "we now derive a pose uncertainty constraint set that contains the true pose with high probability."
- Quaternion formulation: A rotation representation using unit quaternions, advantageous for numerical stability and lower-dimensional parameterizations. "using infinity-norm keypoint constraints and a quaternion formulation."
- Relaxation hierarchy: A sequence of increasingly tight convex relaxations (e.g., via SOS) that converge to the exact solution in the limit. "a hierarchy of relaxations which is guaranteed to converge to the true minimum volume ellipsoid."
- Relaxation order: The degree of the polynomial multipliers in an SOS relaxation, controlling the tightness and computational cost. "The quantity is called the relaxation order."
- Rodrigues' rotation formula: A formula expressing a rotation matrix from an axis and angle using skew-symmetric matrices. "according to Rodrigues' rotation formula~\cite[Ch. 6.2]{Barfoot17book}."
- Semidefinite program: A convex optimization problem with linear matrix inequality constraints, solvable by interior-point methods. "It can be efficiently expressed as a semidefinite program by converting the SOS inequality into a linear matrix inequality."
- Semidefinite relaxation: A technique that relaxes a non-convex problem into a semidefinite program to obtain tractable outer bounds. "use a semidefinite relaxation to maximize the pose error consistent with the keypoint bounds."
- Special Orthogonal group (SO(3)): The Lie group of 3×3 rotation matrices with unit determinant, representing 3D rotations. "$\*R\in\mathrm{SO}(3)$"
- Split conformal prediction: A conformal prediction approach that uses a held-out calibration set to produce finite-sample coverage guarantees. "using split conformal prediction"
- SOS S-lemma: A sum-of-squares strengthened version of the S-lemma that uses polynomial multipliers to certify inclusion. "to derive an SOS S-lemma and extend the ellipsoid procedure into a hierarchy"
- Sum-of-squares (SOS) programming: A convex optimization framework that certifies polynomial nonnegativity via semidefinite constraints. "use ideas from sum-of-squares (SOS) programming"
- Union bound: A probability inequality bounding the probability of a union by the sum of individual probabilities, used to aggregate coverage. "the result follows from a union bound."
- Vectorization operator (vec): The operation that stacks a matrix’s columns into a single vector, enabling algebraic manipulations. "use the operator to denote the vectorization of a matrix by stacking its columns."
Collections
Sign up for free to add this paper to one or more collections.