Aleatoric Uncertainty from AI-based 6D Object Pose Predictors for Object-relative State Estimation (2509.01583v1)

Abstract: Deep Learning (DL) has become essential in various robotics applications due to excelling at processing raw sensory data to extract task specific information from semantic objects. For example, vision-based object-relative navigation relies on a DL-based 6D object pose predictor to provide the relative pose between the object and the robot as measurements to the robot's state estimator. Accurately knowing the uncertainty inherent in such Deep Neural Network (DNN) based measurements is essential for probabilistic state estimators subsequently guiding the robot's tasks. Thus, in this letter, we show that we can extend any existing DL-based object-relative pose predictor for aleatoric uncertainty inference simply by including two multi-layer perceptrons detached from the translational and rotational part of the DL predictor. This allows for efficient training while freezing the existing pre-trained predictor. We then use the inferred 6D pose and its uncertainty as a measurement and corresponding noise covariance matrix in an extended Kalman filter (EKF). Our approach induces minimal computational overhead such that the state estimator can be deployed on edge devices while benefiting from the dynamically inferred measurement uncertainty. This increases the performance of the object-relative state estimation task compared to a fix-covariance approach. We conduct evaluations on synthetic data and real-world data to underline the benefits of aleatoric uncertainty inference for the object-relative state estimation task.

• The paper introduces a method to extend any pre-trained 6D pose predictor with additional MLP heads for estimating translational and rotational aleatoric uncertainty.
• It models uncertainties as multivariate Gaussians and integrates them as dynamic measurement covariances in an EKF, yielding improved state estimation performance.
• Experimental results on synthetic and real-world datasets show that dynamic anchor switching reduces RMSE and improves robustness against ambiguous object poses.

Aleatoric Uncertainty from AI-based 6D Object Pose Predictors for Object-relative State Estimation

Introduction and Motivation

This work addresses the integration of aleatoric uncertainty estimation into deep learning-based 6D object pose predictors for object-relative state estimation in robotics. The central motivation is to enable robust probabilistic state estimation by quantifying the inherent noise in DNN-based pose predictions, which is critical for downstream tasks such as navigation and manipulation. The proposed method extends any pre-trained 6D object pose predictor with two additional MLP heads for independent inference of translational and rotational uncertainty, modeled as multivariate Gaussians. These predicted uncertainties are then used as dynamic measurement covariance matrices in an EKF, replacing fixed, expert-tuned covariances and facilitating improved estimator performance and ease of deployment.

Network Architecture and Aleatoric Uncertainty Modeling

The approach builds on the PoET framework, which predicts 6D object poses directly from RGB images using a transformer-based architecture. The extension consists of two additional MLP heads, one for translation and one for rotation, each outputting a $3 \times 3$ diagonal covariance matrix representing the aleatoric uncertainty for the respective components. The rotation is parameterized in axis-angle form, and the uncertainty is interpreted as the variance in both the axis direction and the rotation angle.

Figure 1: Visualization of predicted aleatoric uncertainty for 6D pose, showing separate uncertainty bounds for position and rotation in axis-angle space.

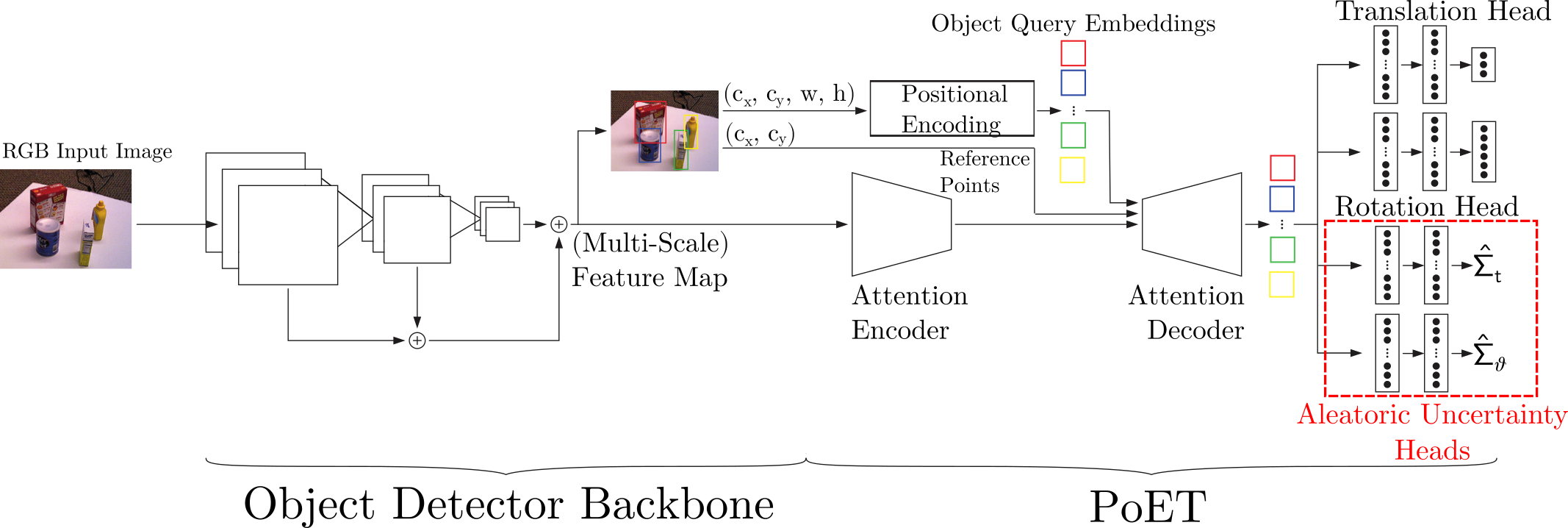
Figure 2: Extension of PoET architecture with independent MLP heads for aleatoric uncertainty prediction, enabling modular calibration and minimal computational overhead.

The loss function is derived from the negative log-likelihood of a multivariate Gaussian, allowing for either joint or separate training of the pose and uncertainty heads. For numerical stability, the network predicts the log-variance, following best practices in uncertainty modeling. The independence of the uncertainty heads enables rapid calibration by freezing the pre-trained pose predictor and training only the uncertainty heads, which is shown to be sufficient for high-quality uncertainty estimation.

Integration with Object-relative State Estimation

The predicted pose and uncertainty are used as measurements and dynamic measurement covariance matrices in an EKF-based state estimator (MaRS). The measurement covariance is constructed by stacking the translation and rotation covariances, both expressed in the camera frame and transformed as required. This dynamic uncertainty enables stochastic anchor object switching, where the object with the lowest predicted uncertainty is selected as the reference for the navigation frame, improving robustness and reducing outlier influence.

Experimental Evaluation

Synthetic and Real-world Datasets

Experiments are conducted on synthetic datasets generated with NVIDIA IsaacSim for power pole and YCB-V objects, as well as real-world UAV inspection data. The pose predictor is trained on 100,000 synthetic images and validated on 20,000 images. The additional computational cost of the uncertainty heads is negligible (0.6% increase in inference time on Jetson Orin AGX).

Figure 3: Examples of synthetic images for power pole and YCB-V objects, with insulator numeration for result discussion.

Uncertainty Calibration and Analysis

Both end-to-end and calibration-only training schemes for the uncertainty heads yield comparable pose accuracy (3 cm translation, $2^\circ$ rotation error). The predicted uncertainties are evaluated using the Prediction Interval Coverage Probability (PICP) metric at 95% confidence, consistently achieving scores above 0.9 for most components, indicating well-calibrated uncertainty but slight overestimation.

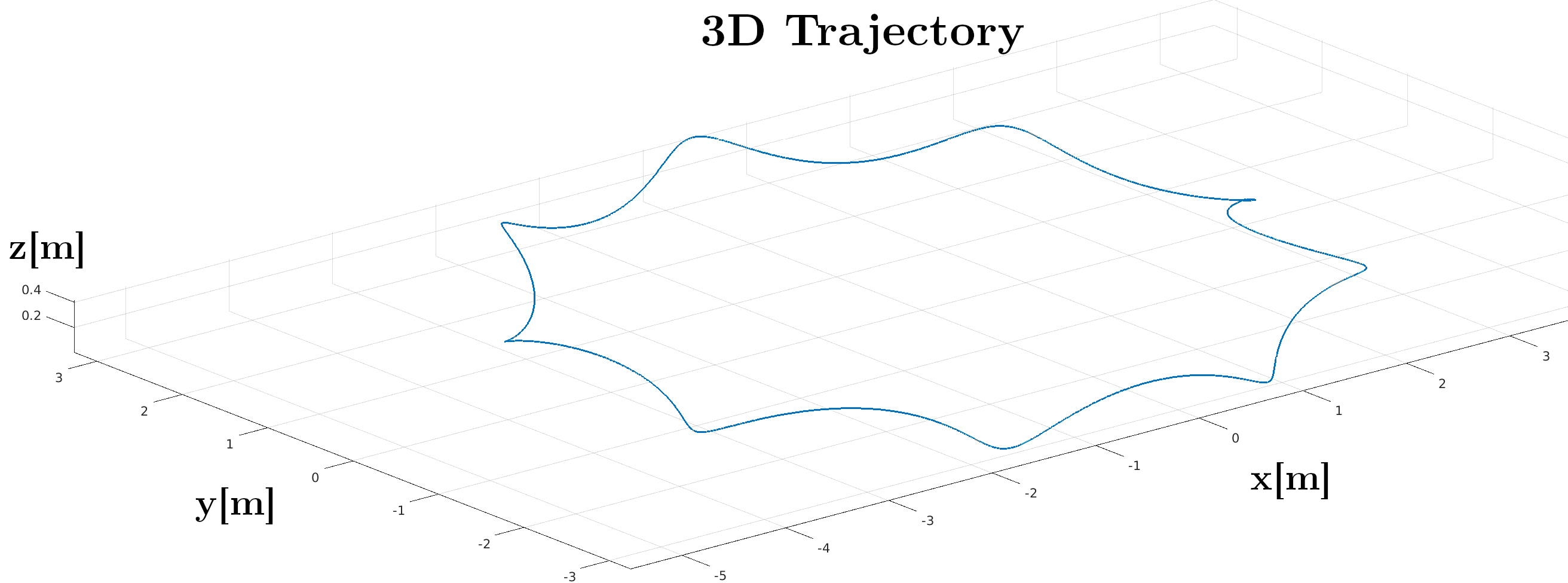
Figure 4: Visualization of a synthetic UAV trajectory used for uncertainty analysis, covering diverse viewpoints and distances.

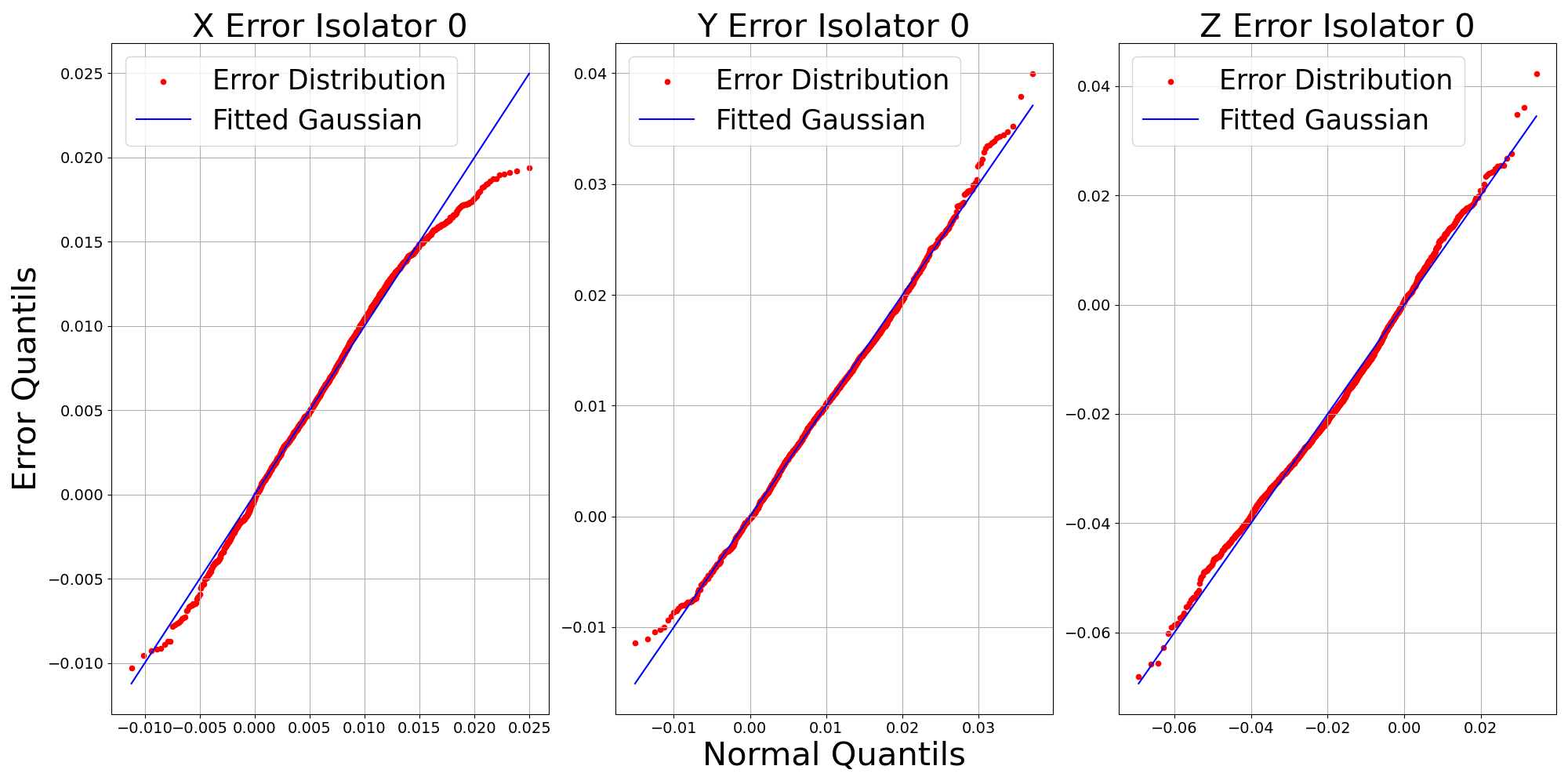
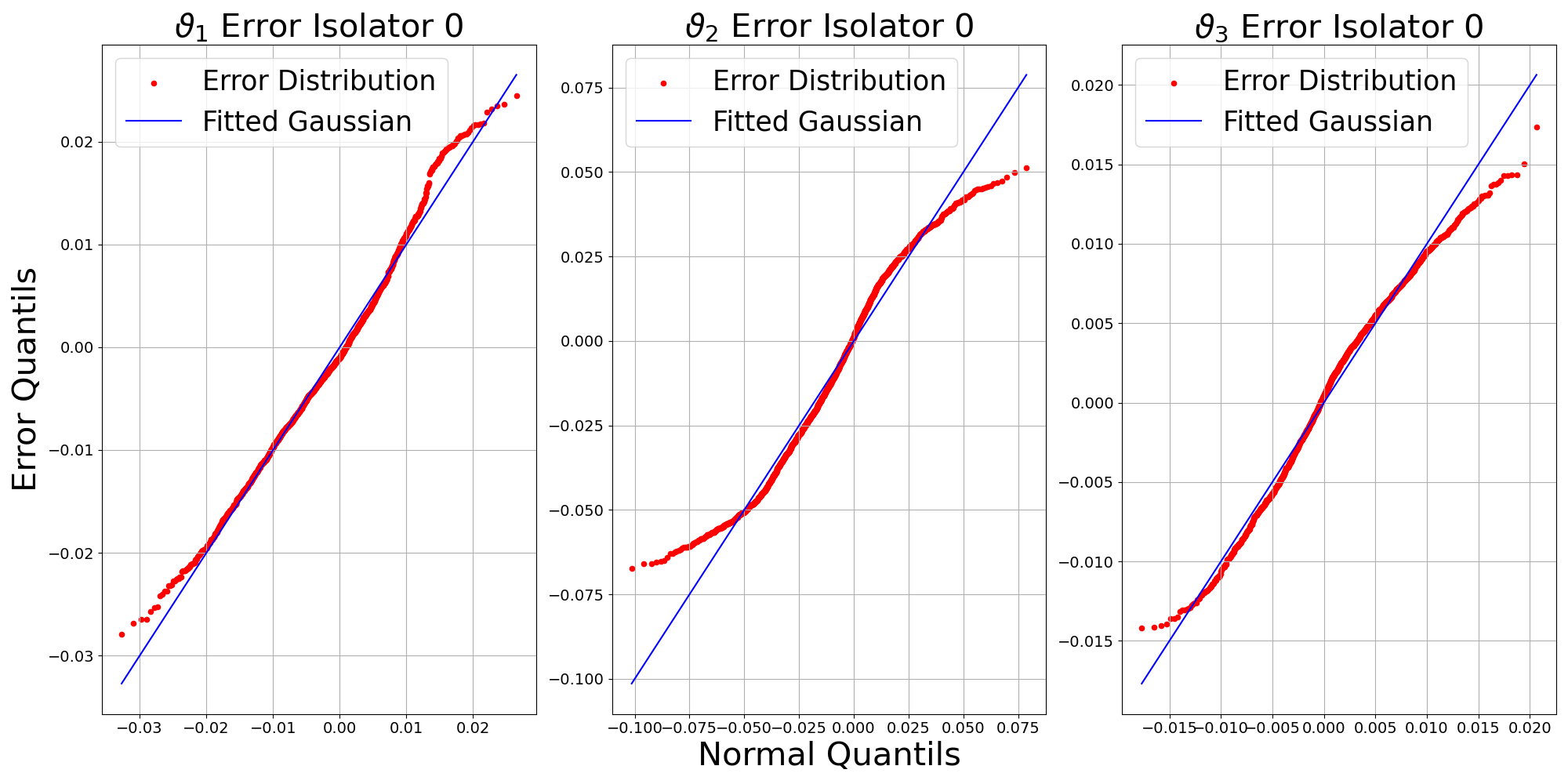
Figure 5: Q-Q plot comparing error distributions for translation and rotation to fitted Gaussians, supporting the modeling assumption of Gaussian error.

Componentwise analysis reveals that the predicted uncertainty tracks the actual error closely, with strong correlation to object distance, especially for translation along the camera's $z$-axis. For ambiguous or symmetric objects (e.g., mug, scissors), rotational uncertainty is higher, and outlier rejection (AOR) can be performed by thresholding the predicted uncertainty.

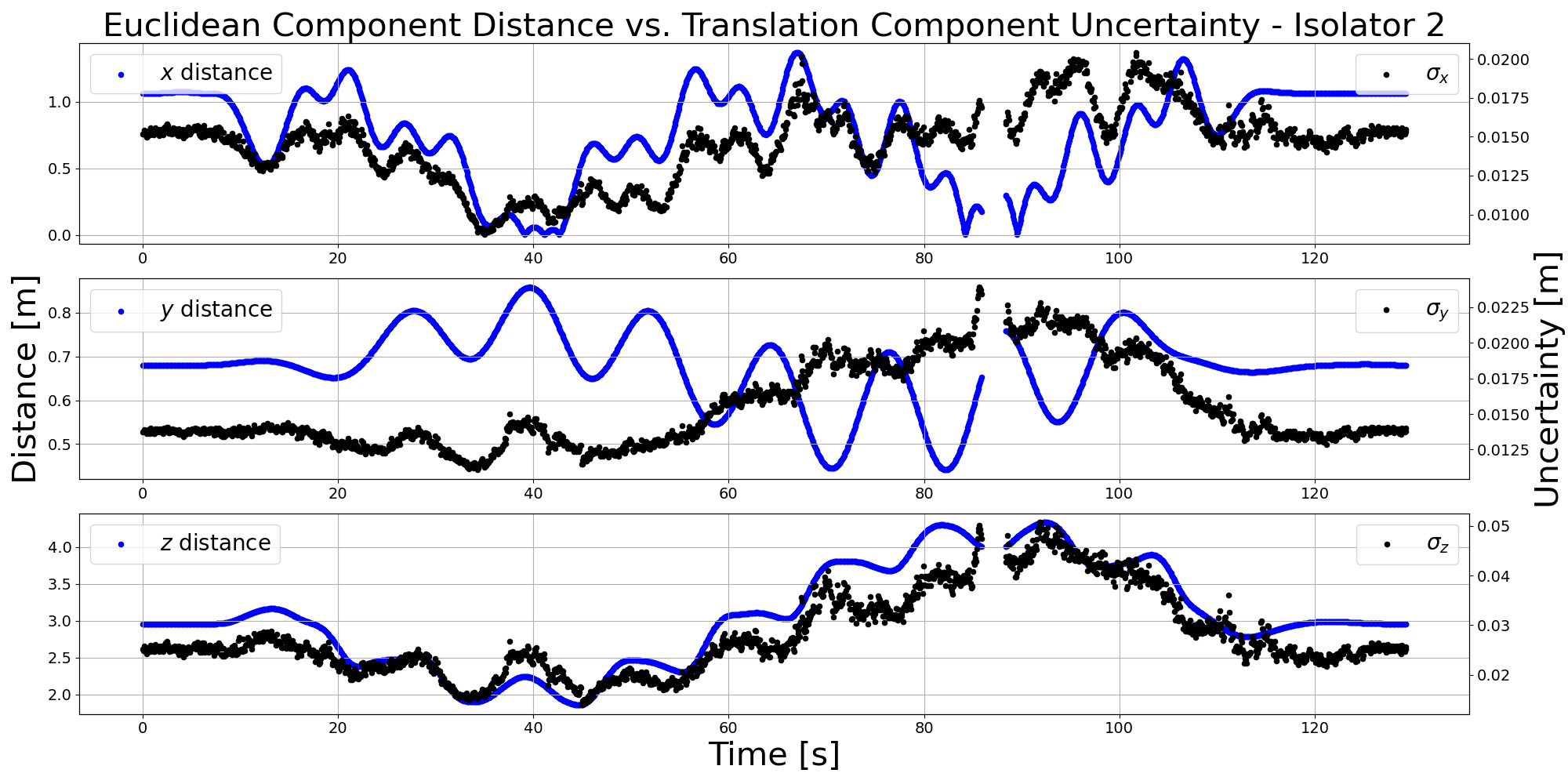
Figure 6: Comparison of absolute rotation error and estimated aleatoric uncertainty for insulator $I_0$ (left), and distance vs. uncertainty for $I_2$ (right), demonstrating dynamic adaptation to viewpoint and object distance.

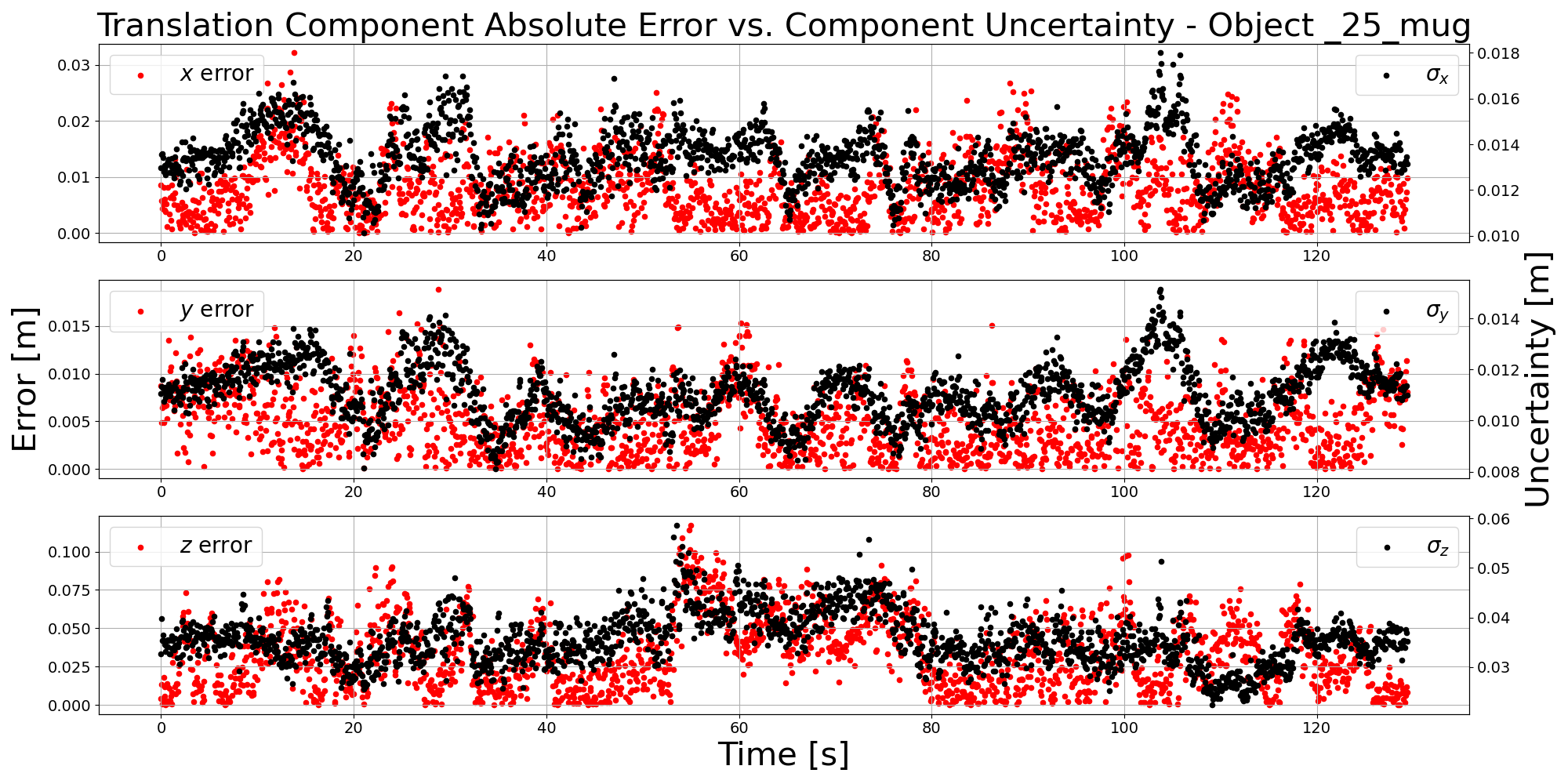
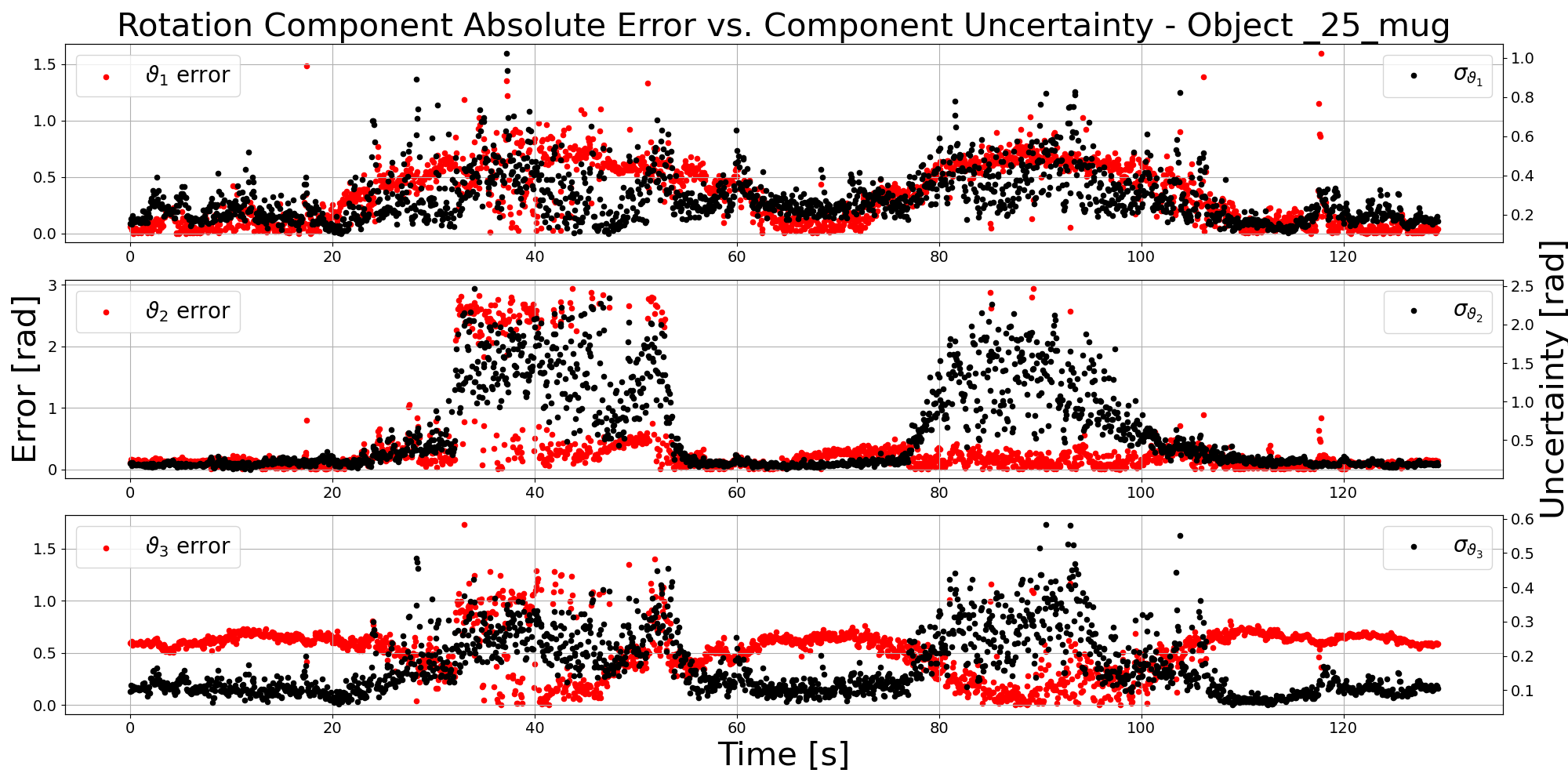
Figure 7: Comparison of translation and rotation error to estimated aleatoric uncertainty for the mug, highlighting increased uncertainty in ambiguous scenarios.

Impact on State Estimation

Three approaches to measurement covariance are compared: fixed (empirically determined), dynamic (predicted aleatoric), and dynamic with anchor object switching. Across five synthetic trajectories, dynamic anchor switching yields the lowest RMSE and maximum position error, outperforming both fixed and dynamic-only approaches. Similar improvements are observed on real-world UAV data, demonstrating transferability from synthetic to real domains. For YCB-V objects, aleatoric uncertainty combined with AOR significantly reduces RMSE for both position and orientation compared to fixed covariance.

Implications and Future Directions

The results demonstrate that aleatoric uncertainty prediction via modular MLP heads is sufficient for robust, dynamic measurement covariance estimation in object-relative state estimation. This eliminates the need for expert tuning and enables stochastic anchor selection, improving estimator performance and resilience to outliers. The method is computationally efficient and suitable for deployment on edge devices, with successful transfer from synthetic to real-world data.

Theoretically, the work supports the modeling of pose prediction error as Gaussian and highlights the importance of uncertainty quantification for reliable sensor fusion. Practically, it enables scalable deployment of DNN-based state estimators in robotics without manual calibration. Future research may explore joint modeling of aleatoric and epistemic uncertainty, cross-correlation in covariance estimation, and integration with optimization-based state estimation frameworks.

Conclusion

This paper presents a practical method for extending any deep learning-based 6D object pose predictor with aleatoric uncertainty estimation, modeled as multivariate Gaussians and inferred via independent MLP heads. The predicted uncertainty serves as dynamic measurement covariance in EKF-based object-relative state estimation, enabling improved performance, dynamic anchor switching, and outlier rejection. The approach is validated on synthetic and real-world datasets, demonstrating negligible computational overhead and strong transferability. These findings have significant implications for robust, scalable deployment of AI-based state estimation in robotics and related domains.