Geometry of Decision Making in Language Models (2511.20315v1)

Abstract: LLMs show strong generalization across diverse tasks, yet the internal decision-making processes behind their predictions remain opaque. In this work, we study the geometry of hidden representations in LLMs through the lens of \textit{intrinsic dimension} (ID), focusing specifically on decision-making dynamics in a multiple-choice question answering (MCQA) setting. We perform a large-scale study, with 28 open-weight transformer models and estimate ID across layers using multiple estimators, while also quantifying per-layer performance on MCQA tasks. Our findings reveal a consistent ID pattern across models: early layers operate on low-dimensional manifolds, middle layers expand this space, and later layers compress it again, converging to decision-relevant representations. Together, these results suggest LLMs implicitly learn to project linguistic inputs onto structured, low-dimensional manifolds aligned with task-specific decisions, providing new geometric insights into how generalization and reasoning emerge in LLMs.

• The paper demonstrates that intrinsic dimension peaks in mid-layers and collapses as LLMs commit to decisions.
• It employs MLE, TwoNN, and GRIDE estimators to quantify layerwise geometry across 28 transformer models in MCQA settings.
• Findings imply that early compression correlates with higher model confidence, efficient generalization, and informs architecture selection.

Geometric Structure of Decision Making in LLMs

Introduction and Motivation

LLMs such as LLaMA, Pythia, GPT-2, and their derivatives demonstrate high proficiency on a range of reasoning and comprehension tasks, yet the internal mechanics by which they transform contextual input into discrete task-specific decisions remain under-explored. The paper "Geometry of Decision Making in LLMs" (2511.20315) advances understanding in this domain by providing a large-scale, layerwise geometric analysis of hidden representations in transformer-based LLMs through the prism of intrinsic dimension (ID). This analysis is conducted with an emphasis on the decision formation process in multiple-choice question answering (MCQA) tasks, which allows precise localization of representational transitions from contextual abstraction to high-confidence commitment.

Methodological Foundation: Intrinsic Dimension and Representation Extraction

The core methodological advance is the systematic quantification of ID across all layers for 28 open-weight transformer models, leveraging a suite of estimators: Maximum Likelihood Estimation (MLE), Two Nearest Neighbors (TwoNN), and the recently introduced Generalized Ratios Intrinsic Dimension Estimator (GRIDE).

Figure 2: Diagrammatic overview of intrinsic dimension estimators (MLE, TwoNN, GRIDE) leveraging local neighborhood statistics for manifold dimensionality estimation.

Importantly, while the extrinsic (hidden) dimension $d$ is fixed by model architecture (e.g., 4096 in LLaMA-7B), the learned feature vectors at each transformer block are empirically supported on low-dimensional, evolving manifolds. Intermediate and output states (notably MLP output and residual post-activation) are extracted for the final (decision) token at each block, corresponding to the predicted answer in MCQA settings.

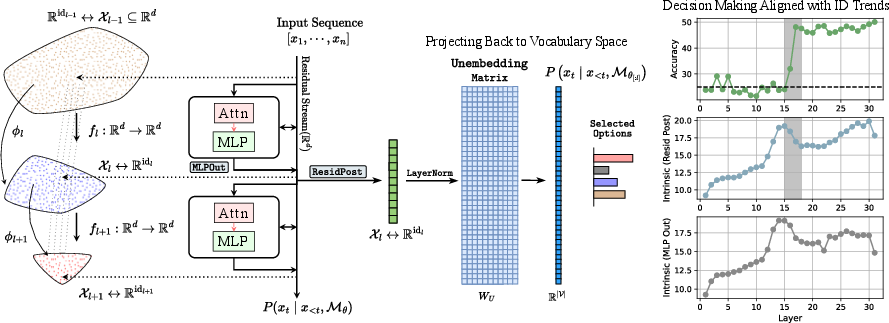
Figure 3: Transformers process fixed-$d$ vectors across layers, but the real feature manifold $\mathbb{R}^d$ varies in intrinsic dimension, demonstrating layerwise compression and expansion.

Main Empirical Results: Hump-Shaped ID and Decision Transitions

Across a spectrum of model architectures and tasks, the following central geometric phenomenon is robustly observed: the ID first increases in the initial layers, peaks at a point typically corresponding to the network's abstraction phase, and then sharply decreases in deeper layers. This results in a "hunchback"-shaped profile when plotting ID against layer index, consistently mirrored across both synthetic (arithmetic, greater-than) and real-world (e.g., AGNews, MMLU, COPA) MCQA datasets.

Representative visualizations on STEM and causal reasoning tasks provide concrete confirmation:

Figure 4: Alignment of accuracy gain and ID peak in LLaMA variants on MMLU STEM—peak ID marks the phase immediately preceding decisive jump in task confidence.

Figure 5: Similar ID-accuracy alignment emerges for causal reasoning (COPA), with ID drop coincident with accuracy surge.

Crucially, abrupt accuracy increases nearly always follow or coincide with the ID peak, particularly evident in reasoning-heavy datasets. This supports the hypothesis that the network's internal commitment to a particular answer (i.e., decisiveness) is geometrically encoded as a collapse of the feature manifold's intrinsic dimensionality immediately after the abstraction peak.

Architectures, Training, and Prompt Conditioning

An analysis across architectures and model sizes demonstrates that both depth and model capacity affect the geometry of decision formation. Larger models reach ID peaks earlier (in relative depth) and achieve lower post-peak IDs, indicative of more efficient abstraction and earlier commitment. This is consistent across LLaMA, Pythia, Gemma, and other families.

Residual post-activation vs. MLP output representations show distinct geometric behaviors: MLP outputs feature sharper, more localized ID transitions, functioning as targeted task refocusing points, while residual post-activations display smooth, monotonous ID evolution—reflecting integrated semantic stabilization.

Figure 7: Layerwise comparison of ID for MLP output and residual post-activation in MMLU STEM; sharper transitions are present in MLP output.

Prompt conditioning further modulates internal geometry. Inclusion of increasing few-shot examples in context reduces final-layer ID and sharpens the compression transition phase, especially in larger models.

Figure 1: Boxplot of last-layer ID (MLP Out) across 28 models, showing monotonic decrease as more in-context examples are provided.

Figure 9: In arithmetic tasks, increased few-shot examples (0 to 50) reduce ID and improve accuracy, especially for high-capacity Pythia models.

The observation is that model generalization and sample efficiency in ICL settings are coupled with effective compression of the context into a low-dimensional, decision-aligned manifold.

Task Complexity and Generalization

ID reflects not just model-internal processing, but also input and task complexity. Across the model zoo and multiple real-world datasets (e.g., AGNews, SST2, Rotten Tomatoes, MMLU), the last-layer ID for high-performing models is consistently low (5–37), far below the extrinsic dimension (d=768–4096). This implies that task-relevant semantic information, even for complex reasoning, is represented on highly compressed manifolds.

Correlation analysis—e.g., across LLaMA variants—demonstrates moderately negative correlation between last-layer ID and final task accuracy in some datasets (Spearman range −0.5 to −0.94 for sentiment/language tasks), but not universally so on all tasks. Thus, while lower ID aligns with higher confidence/expertise, ID alone cannot universally serve as an unsupervised accuracy proxy.

Dynamics Throughout Training

Monitoring ID through training trajectories (using Pythia family checkpoints on controlled arithmetic tasks) reveals that while the hunchback trend arises increasingly over training, the compression phase becomes more pronounced as the model transitions from memorization to generalization, coinciding with the emergence of confident, decisive predictions.

Figure 10: Pythia training dynamics; the reverse peak in ID precedes accuracy rises as semantic discrimination is acquired.

Synthesis and Theoretical Implications

The primary theoretical implication is that LLMs' decision processes manifest as a geometric transition: from low-dimensional context encoding through expansion and abstraction, back to a decisive collapse into a compressed, task-aligned, low-dimensional manifold. This geometrization aligns with information-theoretic approaches, supporting recent findings that geometric and entropic compression co-occur and predict adaptation and generalization capacity.

These findings suggest several new functional perspectives:

• Identification of Decision Layers: The ID peak serves as a geometric marker for the layer at which the model's internal commitment to a decision first crystallizes. This enables principled interpretability and intervention on where and when semantic commitments/formations occur within the forward pass.
• Manifold Compression as a Proxy for Confidence: The coarse-to-fine ID trajectory encodes the degree of representational focus, supporting potential unsupervised metrics for confidence, reasoning saturation under ICL, and the degree of overfitting or memorization.
• Architectural and Training Regime Selection: The observation that certain architectures and training regimes yield faster, earlier compression—thus potentially greater reasoning and generalization efficiency—may inform model design, compression strategies, and curriculum learning protocols.

Limitations and Avenues for Future Research

Several constraints are noted: analyses are limited to deterministic, non-generative MCQA tasks; only the last token is analyzed, not the full sequence. ID estimators, while robust, still display sensitivity/noise and possible underestimation in highly multimodal manifolds. The link between ID and information-theoretic metrics (e.g., entropy, mutual information) remains only partially formalized. Further, cross-model and cross-lingual geometric alignment remains unaddressed.

Future work should pursue:

• Extending geometric analysis to open-ended, generative settings and sequence-wide decision making.
• Linking geometric compression with explicit entropy regulation mechanisms (e.g., entropy neurons [Stolfo NeurIPS 2025]).
• Comparative manifold alignment between models, modalities, and fine-tuning protocols.
• Development of practical geometric proxies for automatic model and in-context example selection.

Conclusion

This paper provides substantial empirical evidence that transformer-based LLMs, regardless of their extrinsic size, internally form and then collapse high-dimensional abstractions into compact, decision-bound manifolds as they resolve meaningful predictions. The consistent, architecture- and task-agnostic geometric patterns uncovered—validated through comprehensive measurement of intrinsic dimensionality—reveal fundamental characteristics of how LLMs generalize, focus, and commit to decisions. These results strongly motivate further geometric interpretability work, aiming toward a precise, unified account of abstraction, decisiveness, and generalization dynamics in deep sequence models.

(2511.20315)