SSR: Socratic Self-Refine for Large Language Model Reasoning (2511.10621v1)
Abstract: LLMs have demonstrated remarkable reasoning abilities, yet existing test-time frameworks often rely on coarse self-verification and self-correction, limiting their effectiveness on complex tasks. In this paper, we propose Socratic Self-Refine (SSR), a novel framework for fine-grained evaluation and precise refinement of LLM reasoning. Our proposed SSR decomposes model responses into verifiable (sub-question, sub-answer) pairs, enabling step-level confidence estimation through controlled re-solving and self-consistency checks. By pinpointing unreliable steps and iteratively refining them, SSR produces more accurate and interpretable reasoning chains. Empirical results across five reasoning benchmarks and three LLMs show that SSR consistently outperforms state-of-the-art iterative self-refinement baselines. Beyond performance gains, SSR provides a principled black-box approach for evaluating and understanding the internal reasoning processes of LLMs. Code is available at https://github.com/SalesforceAIResearch/socratic-self-refine-reasoning.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces a new way to help AI LLMs think more clearly and correctly. The method is called Socratic Self-Refine (SSR). It teaches a model to break its reasoning into small steps, check each step carefully, and fix the ones that seem wrong. The goal is to make the model’s answers more accurate and easier to understand.
Key Questions the Paper Tries to Answer
- How can we catch small mistakes inside a long chain of reasoning before they cause big errors?
- Can a model judge which parts of its own thinking are trustworthy?
- If we fix the weakest steps first, will the final answer improve?
- Can we do all of this without retraining the model—only by smart prompting at test time?
How the Researchers Approached the Problem
The Core Idea: “Socratic steps”
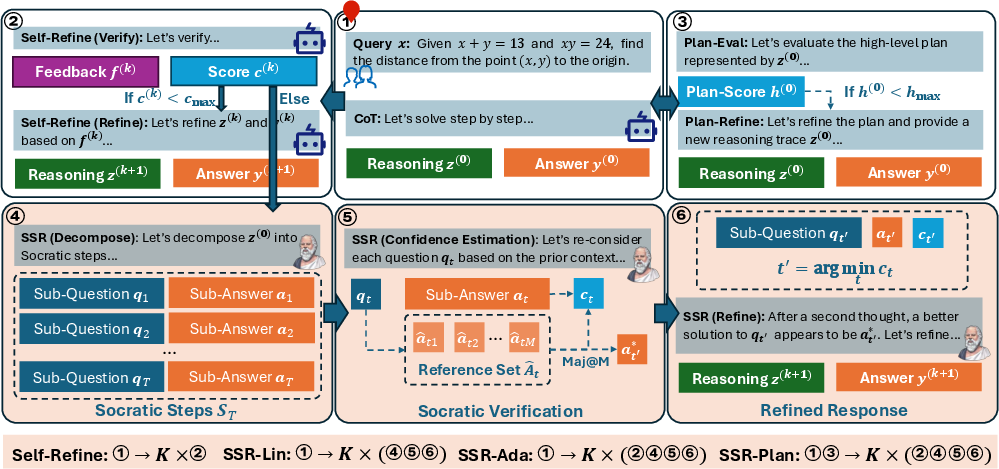
Think of solving a problem like a teacher using the Socratic method: asking a series of small questions and answering them one by one. SSR turns a model’s long explanation into a list of paired mini-steps:
- A sub-question (what to do next)
- A sub-answer (the result of that mini-step)
This is like showing your work in math and labeling each line clearly.
Step-Level Confidence by “Re-solving”
To find shaky steps, SSR asks the model to solve each mini-question multiple times independently. If the answers mostly agree, the model is likely confident. If the answers don’t match, that step might be unreliable.
Everyday analogy: If you do the same small calculation five times and get the same result four or five times, you probably trust it. If you keep getting different results, you should double-check.
Technical terms in simple words:
- Self-consistency: Re-solving the same sub-question several times and seeing how often the answers match. More matches = higher confidence.
- Majority voting: When multiple tries give different answers, pick the one that appears the most often.
The Refinement Loop
Once SSR finds the weakest step (the one with the lowest confidence):
- It decides on a better sub-answer using majority voting.
- It feeds that corrected sub-answer back into the model.
- The model updates the whole explanation so it fits the fixed step.
- Repeat until things look stable.
This is like correcting the line where your algebra went off, then rewriting the rest so it all makes sense again.
Variants for Efficiency and Planning
To balance speed and quality, the paper tests three versions:
- SSR-Lin: Always do the full “decompose, verify, refine” steps each time.
- SSR-Ada: Try a simpler self-refine first. If no clear mistake is found, then use the full SSR. This saves time when answers are already good.
- SSR-Plan: Before refining steps, check the high-level plan (the overall outline). If the plan is weak, improve it once, then do SSR. This helps the model start on the right path.
All of this works as a “black-box” method: you don’t change the model’s internal code; you just ask it better questions and use smart prompts.
Main Findings and Why They Matter
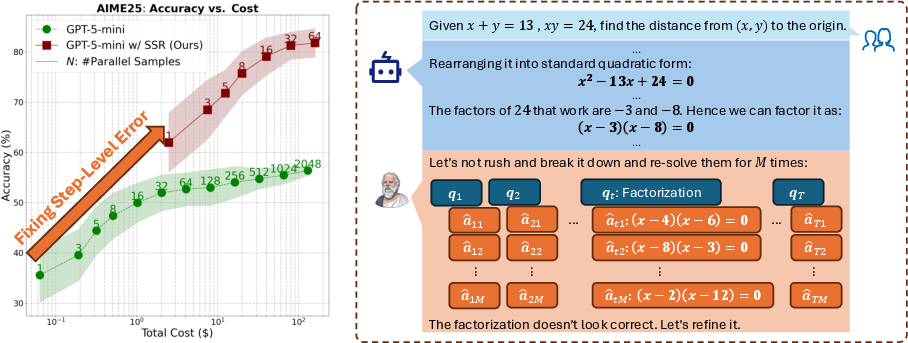
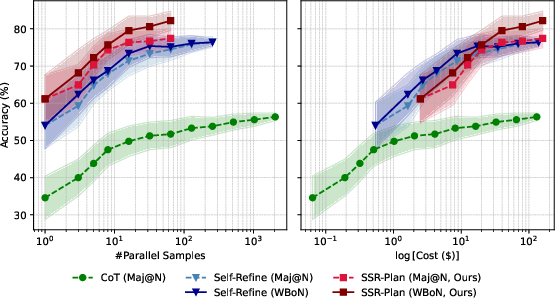
Across five reasoning benchmarks (tough math problems and logic puzzles like Zebra and Mini-Sudoku) and multiple models, SSR beats other test-time refinement methods.
Key takeaways:
- SSR improves accuracy by fixing specific step-level mistakes rather than just giving general feedback.
- It scales well when you run several attempts in parallel and use majority voting (it doesn’t just plateau like standard “Chain-of-Thought” can).
- SSR-Plan often performs best on challenging tasks because a strong plan reduces downstream errors.
- SSR-Ada is efficient: it avoids the heavy SSR process unless it’s really needed, yet still gains accuracy.
Why this matters:
- More accurate: Fewer “cascading errors” where one wrong step ruins the whole solution.
- More interpretable: The model’s reasoning is broken into clear question-answer pairs, so you can see what went wrong and where.
- More trustworthy: It helps build systems that can check themselves and explain their fixes.
Implications and Potential Impact
- Better AI tutors and assistants: SSR can help models explain homework solutions step-by-step, spot mistakes, and fix them in a way that teaches the reasoning.
- Safer decision-making: In areas like coding, math, or logical planning, catching errors early prevents bigger failures later.
- Test-time tools for any model: Because SSR is a black-box approach, it can upgrade many existing models without retraining.
- Research direction: Encourages a shift from judging only final answers to evaluating and improving the process itself, leading to more reliable and controllable AI reasoning.
In short, SSR turns “just write your thinking” into “ask precise mini-questions, check your steps, fix the weakest link, and keep going.” That simple idea helps AI think more like a careful student—and get better answers.
Knowledge Gaps
Below is a concise list of the key knowledge gaps, limitations, and open questions left unresolved by the paper. Each point is phrased to be actionable for future research.
- Faithfulness of Socratic decomposition: No quantitative evaluation that the extracted (sub-question, sub-answer) steps are faithful to the model’s original reasoning or to an oracle “true” decomposition; unclear how decomposition errors affect downstream refinement.
- Non-uniqueness of decompositions: The framework assumes a valid linearization exists but does not paper how different valid decompositions (or graph-structured vs. linear traces) change confidence estimation and refinement outcomes.
- Step granularity selection: No principled method to choose or adapt the granularity of steps; missing analysis of how under-/over-segmentation impacts accuracy, stability, and compute.
- Calibration of step-level confidence c_t: Self-consistency-based confidence lacks calibration analysis; no correlation paper with true step correctness across tasks, nor comparison to alternative uncertainty estimates (e.g., token-level entropy, verifier scores).
- Context-free equivalence judging: The assumption that step correctness can be judged context-free is untested for tasks where meaning depends on context (variable bindings, scope, constraints); need empirical tests and failure analyses.
- M (re-solving count) sensitivity: No ablation of how the number of re-solves (M) trades off cost vs. accuracy; no adaptive allocation (e.g., more re-solves for contentious steps).
- Choice of step-to-refine policy: Always refining the minimum-confidence step is heuristic; no comparison with alternative selection policies (e.g., top-k steps, expected global impact, beam over refinements).
- Plan–execution independence assumption: The factorization that separates high-level planning from execution is unverified; no empirical tests quantifying when this assumption holds or harms performance.
- Plan quality assessment: The “single-round” plan refinement is ad hoc; lacking standardized plan-quality metrics, verifier checks, or iterative planning strategies; no paper of plan errors propagating to execution.
- Gating/controller design: The adaptive trigger for invoking SSR when Self-Refine “finds no mistakes” is heuristic; no learned or theoretically grounded controller, nor analyses of false positives/negatives and their cost implications.
- Convergence and stopping: No formal or empirical convergence criteria; no analysis of oscillations/degradation across iterations; stopping conditions are fixed (K) rather than calibrated.
- Compute and fairness accounting: Claims of “comparable computational cost” are not substantiated with wall-clock time, token counts, or API-call parity; missing cost–accuracy Pareto curves against baselines.
- Robustness to decoding settings: Sensitivity to temperature, top-p, seed, and sampling strategies (for both CoT and re-solves) is unreported; lack of robustness analyses.
- Domain generalization: Evaluation limited to math and synthetic logic; no tests on code generation, multi-hop QA, scientific reasoning, tool-augmented tasks, retrieval-heavy settings, or multimodal reasoning.
- Step verification beyond math: For non-math domains, deterministic equivalence checking is unclear; reliance on LLM-as-judge for step equivalence is unvalidated and may be biased.
- External verifiers/tools: The framework does not integrate symbolic solvers, program executors, or rule engines to verify steps; unclear gains when hybridizing SSR with tool-based verification.
- Interpretability claims: While SSR is argued to be more interpretable, there is no human paper or metrics (e.g., usability, trust calibration, error localization quality) to substantiate interpretability benefits.
- Error taxonomy and failure modes: No systematic analysis of which error types (algebraic slips, misapplied rules, plan errors, semantic misunderstandings) are best addressed by SSR vs. when it fails.
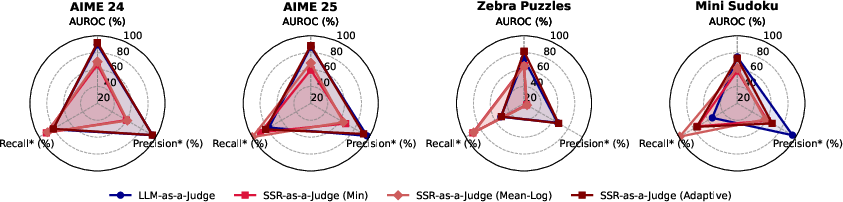
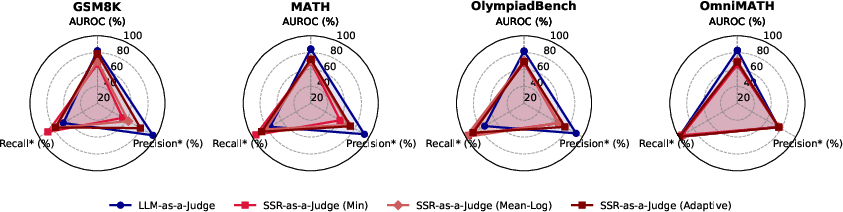
- Data leakage and judge bias: Best-of-K and non-numeric HLE evaluation rely on LLM-as-a-Judge; no assessment of judge biases, position effects, model-family circularity, or agreement with human judgments.
- Reproducibility and model dependence: Heavy dependence on closed-source models (GPT-4.1-nano, GPT-5-mini/5) limits reproducibility; no results with strong open models, nor guidance for replicating with publicly available backbones.
- Step formatting and context management: Only preliminary ablations on “natural vs. Socratic” context are provided; no systematic exploration of structured formats (JSON, XML), schema choices, and their effects on performance.
- Scalability with long contexts: No evaluation under long-horizon reasoning or near context-window limits; unclear performance and memory costs for very long chains.
- Interaction with search-based methods: SSR is not combined with search (e.g., MCTS on steps, beam over plans); open question whether joint search over plan and step refinements yields further gains.
- Hyperparameter tuning and overfitting: No transparency on tuning procedures for M, K, N, prompt templates, and thresholds; risk of test-set overfitting not addressed with held-out validation.
- Safety and reliability under adversarial inputs: No robustness assessment under adversarial prompts, noisy or misleading steps, or deceptive decompositions generated by the model itself.
- Handling missing or poor initial CoT: SSR assumes an initial trace suitable for decomposition; failure modes where initial CoT is minimal/incorrect or when the model resists producing CoT are not studied.
- Generalization to multilingual settings: The approach is only tested in English; applicability to multilingual reasoning (and cross-lingual decomposition/verification) is open.
- Cost-aware scheduling: No mechanism to dynamically allocate compute across examples based on predicted difficulty or early confidence signals; potential for large efficiency gains remains unexplored.
- Theoretical guarantees: No theoretical analysis of when SSR improves expected accuracy over self-refine or CoT, nor bounds on error reduction from targeted step refinement.
Practical Applications
Immediate Applications
Below are actionable use cases that can be deployed now by leveraging the paper’s Socratic Self-Refine (SSR) framework and its variants (SSR-Lin, SSR-Ada, SSR-Plan). Each entry includes relevant sectors, example tools/workflows, and assumptions or dependencies that affect feasibility.
- LLM guardrails for reasoning-heavy workloads
- Sectors: software, finance, data analytics, customer support
- Tools/workflows: SSR microservice/API for step-level confidence scoring and targeted refinement; LangChain/LlamaIndex plugin; confidence dashboards; SSR-based sample selection for test-time scaling (majority vote with confidence aggregation)
- Assumptions/dependencies: LLM must reliably decompose responses into (sub-question, sub-answer) pairs; extra compute for re-solving and confidence estimation; step equivalence often requires LLM judgment or domain-specific verifiers
- Math and logic Q&A systems with higher accuracy and interpretability
- Sectors: education, consumer apps, test prep
- Tools/workflows: math/puzzle solvers using SSR to pinpoint unreliable steps and refine them; SSR-Plan for stronger pre-execution planning; majority voting over sub-answers to avoid cascading errors
- Assumptions/dependencies: tasks resemble verifiable benchmarks (AIME, MATH, Sudoku/Zebra); numeric and rule-based equivalence checking available; latency acceptable for iterative refinement
- Spreadsheet and analytics assistants that verify multi-step calculations
- Sectors: finance, operations, audit
- Tools/workflows: Excel/Google Sheets add-in applying SSR to break complex formulas into steps, compute self-consistency per step, flag low-confidence cells, and auto-refine via majority vote
- Assumptions/dependencies: numeric equivalence checking is reliable; organizational tolerance for added latency and API calls; alignment with data privacy/security requirements
- Educational tutoring and assessment with step-level feedback
- Sectors: education, edtech
- Tools/workflows: AI tutors that present sub-questions, surface step-level confidence, and generate targeted hints; graders that evaluate student CoT traces using SSR’s decomposition and confidence estimation
- Assumptions/dependencies: problems must have verifiable intermediate steps; carefully designed prompts and context management; human-in-the-loop preferred for high-stakes grading
- Research assistance for mathematical derivations and structured logic
- Sectors: academia (STEM), technical writing
- Tools/workflows: SSR-enabled assistant highlighting low-confidence steps in proofs or derivations and proposing refined sub-answers; Overleaf or document review plugins for interpretable audit trails
- Assumptions/dependencies: mapping natural language derivations to checkable sub-steps; may require symbolic math tools (CAS) for robust equivalence beyond LLM self-evaluation
- LLM evaluation, benchmarking, and model selection
- Sectors: AI/ML development, MLOps
- Tools/workflows: black-box process evaluation using SSR confidence scores for sample selection; adaptive gating (SSR-Ada) to control costs while retaining refinement benefits; test-time scaling via confidence-weighted majority vote
- Assumptions/dependencies: extra inference budget for re-solving steps; reliability of confidence prompts; calibration differences between models
- Rule-based data curation and validation
- Sectors: data engineering, knowledge management
- Tools/workflows: SSR applied to tasks with explicit constraints (e.g., small logic puzzles, config checks) to detect and refine inconsistent steps; integration with rule engines
- Assumptions/dependencies: availability of rule-based validators; tasks must be decomposable into discrete, verifiable steps
- Customer support troubleshooting flows
- Sectors: IT services, telecom, consumer electronics
- Tools/workflows: SSR to structure diagnostic decision trees, assign confidence to each step, and auto-refine low-confidence steps or escalate to human agents
- Assumptions/dependencies: clear correctness criteria per step; domain knowledge or external tools may be needed; latency must fit support SLAs
Long-Term Applications
The following use cases require additional research, integration with external systems, domain verification, or scaling efforts before dependable deployment.
- Safety-critical decision support with auditable reasoning
- Sectors: healthcare, legal, public safety
- Tools/workflows: SSR-generated step-level audit trails; integration with medical guideline databases or legal corpora; gated escalation on low-confidence steps; compliance logging
- Assumptions/dependencies: rigorous validation and clinical/legal oversight; robust external verifiers; strong privacy/security; regulatory alignment and certification
- Autonomous agents for planning and execution
- Sectors: robotics, supply chain, field operations
- Tools/workflows: SSR-Plan for high-level plan verification and re-planning; step-level confidence to trigger corrective actions; closed-loop integration with tools, sensors, and environment feedback
- Assumptions/dependencies: reliable mapping from language steps to executable actions; real-time constraints; integration with tool-use and monitoring; domain simulators or validators
- Software engineering copilots with step-wise verification
- Sectors: software, DevOps
- Tools/workflows: IDE extensions that decompose design/algorithmic reasoning into sub-questions; auto-generate unit tests per step; SSR confidence to gate code acceptance; static analysis integration
- Assumptions/dependencies: robust decomposition from natural language to code-level artifacts; high-quality unit tests and analyzers as objective verifiers; performance and latency budgets
- Financial risk analytics and compliance guardrails
- Sectors: finance, insurance, audit
- Tools/workflows: SSR to trace complex modeling pipelines; confidence-weighted review of calculations; automated audit trails for regulators; alerts when key steps are low-confidence
- Assumptions/dependencies: domain-specific validators; integration with enterprise data; stringent governance; model calibration to regulatory standards
- Formal mathematics and proof assistance
- Sectors: academia (math/CS), formal methods
- Tools/workflows: SSR scaffolding aligned to proof assistants (Lean, Coq) to convert sub-answers into formal statements; dual verification via symbolic provers and SSR confidence
- Assumptions/dependencies: translation from natural language reasoning to formal proofs; toolchain maturity; significant research on equivalence and semantics
- Scalable educational authoring and adaptive curricula
- Sectors: education, edtech platforms
- Tools/workflows: large-scale generation of step-annotated solutions, rubrics, and adaptive exercises; student models that incorporate step-level confidence to personalize interventions
- Assumptions/dependencies: fairness and reliability across diverse subjects; robust verifiers for non-numeric domains; longitudinal evaluation and data governance
- AI governance, transparency, and process standards
- Sectors: policy, compliance, enterprise risk
- Tools/workflows: SSR-based “process log” standards for AI outputs; audit toolkits that require step-level confidence and refinement history; certification schemes for high-stakes deployments
- Assumptions/dependencies: consensus standards across industry; auditor training; legal/regulatory adoption; handling sensitive process data
- Enterprise workflow orchestration with confidence-driven escalations
- Sectors: operations, procurement, HR onboarding
- Tools/workflows: BPM systems augmented with SSR to decompose and monitor multi-step processes; automatic routing to humans when steps are low-confidence; continuous refinement of SOPs
- Assumptions/dependencies: precise definition of verifiable sub-steps; integration complexity with existing systems; organizational change management
Notes on cross-cutting assumptions and dependencies:
- SSR depends on reliable decomposition into Socratic steps and meaningful confidence estimation; both are model- and prompt-sensitive.
- Equivalence checking is straightforward for numeric/math steps but requires domain-specific validators or formal tools in open-ended contexts.
- Cost and latency increase due to multiple re-solves and confidence scoring; SSR-Ada’s gating mitigates this but not fully.
- Context management matters: the paper’s ablations favor reflection with natural context over strict Socratic-only formats, implying careful prompt and workflow design.
- Black-box applicability is a strength, but best results often require complementary tools (symbolic solvers, rule engines, unit tests) and human oversight in high-stakes use.
Glossary
- Adaptive SSR (SSR-Ada): An SSR variant that is invoked via a gate only when standard Self-Refine fails to identify errors, balancing efficiency and accuracy. "We denote SSR with this adaptive gating mechanism as Adaptive SSR (SSR-Ada)."
- Atom of Thoughts (AoT): A refinement method that builds a structured graph of reasoning by contracting and solving improved sub-questions. "Atom of Thoughts~(AoT)~\citep{teng2025atom} incrementally constructs a Directed Acyclic Graph (DAG) of reasoning, contracts intermediate results into improved sub-questions, and solves them step by step."
- Best-of-K (BoK-Acc): An upper-bound metric that evaluates the accuracy of the best answer selected among K refinement iterations. "Both BoK-Acc and Pass@K demonstrate that SSR variants yield higher-quality and diverse refinement trajectories compared to baselines."
- Chain-of-Thought (CoT): A prompting style that elicits explicit intermediate reasoning steps to improve interpretability and performance. "Chain-of-Thought (CoT) reasoning~\citep{wei2022chain} approximates this integral with a single sample:"
- Directed Acyclic Graph (DAG): A graph structure with directed edges and no cycles, used to represent structured multi-step reasoning. "Directed Acyclic Graph (DAG) of reasoning"
- Gating mechanism: A control strategy that decides whether to apply SSR based on whether Self-Refine detects errors, reducing unnecessary overhead. "we adopt a gating mechanism that combines Self-Refine~\citep{madaan2023self} with SSR."
- Instruction tuning: A training approach that fine-tunes LLMs to follow natural language instructions, often aligned with CoT-style outputs. "Because most modern LLMs are trained with instruction tuning~\citep{wei2021finetuned} and preference tuning~\citep{ouyang2022training},"
- Joint probability factorization: Decomposing a joint distribution over reasoning steps into products of conditional probabilities for planning and execution. "The joint probability distribution of can be factorized into a product of conditional probabilities:"
- LLM-as-a-Judge: A paradigm where an LLM evaluates and ranks candidate outputs, often aligning with human judgments. "either by LLM-as-a-Judge~\citep{gu2024survey},"
- Linear SSR (SSR-Lin): The version of SSR that applies decomposition, verification, and refinement at every iteration. "We refer to the variant that directly combines the three steps described above as Linear SSR (SSR-Lin)."
- Majority Voting (Maj@N): A test-time aggregation method that selects the most common final answer among N independent reasoning traces. "A common strategy is Majority Voting (Maj@N), which averages over multiple sampled reasoning traces~\citep{wang2022self}:"
- Marginalization: Modeling the final answer by integrating over latent natural-language reasoning traces. "LLM reasoning can be modeled as marginalization over intermediate natural language reasoning traces"
- Monte Carlo Tree Search (MCTS): A search algorithm that explores a decision tree using randomized simulations to select high-value paths. "applying Monte Carlo Tree Search~(MCTS) to search for the best response."
- Monte Carlo Tree Self-Refine (MCTSr): A refinement framework that treats generations as nodes and self-refine steps as edges, using MCTS to find better responses. "Monte Carlo Tree Self-Refine (MCTSr)~\citep{zhang2024accessing} treats the full generation as a node and the self-refine step as an edge, applying Monte Carlo Tree Search~(MCTS) to search for the best response."
- Oracle posterior: The ideal (inaccessible) conditional probability over the true Socratic decomposition given the reasoning trace and answer. "and the oracle posterior is unavailable, we adopt a zero-shot prompting approach"
- Pass@K: An upper-bound metric measuring whether at least one of K refinement iterations produces a correct answer. "Both BoK-Acc and Pass@K demonstrate that SSR variants yield higher-quality and diverse refinement trajectories compared to baselines."
- Plan refinement: A preliminary step that evaluates and improves the high-level plan (sub-questions) before step-level execution refinement. "Plan refinement, summarizes the high-level plan of a reasoning trace, and refines the plan and the trace if necessary;"
- Preference tuning: Training that aligns LLM outputs with human preferences, often reinforcing CoT-like reasoning styles. "Because most modern LLMs are trained with instruction tuning~\citep{wei2021finetuned} and preference tuning~\citep{ouyang2022training},"
- Probabilistic independence: An assumption that sub-question planning is independent of previous answers, enabling a simplified factorization. "By assuming probabilistic independence between each sub-question and the preceding answers ,"
- Self-consistency: A reliability signal derived from the agreement among multiple independent solutions to the same sub-question. "step-level confidence estimation through controlled re-solving and self-consistency checks."
- Self-Refine: An iterative method where the model critiques and revises its own output based on generated feedback. "Self-Refine~\citep{madaan2023self} iteratively generates feedback for a given response and updates the response based on this self-feedback."
- Self-verification: Evaluating the reliability of outputs using model-derived confidence or ranking without external labels. "Sample selection with self-verification, aims to assess response reliability by assigning confidence scores to completed reasoning traces"
- Socratic Feedback: The triplet of the identified low-confidence step’s sub-question, original sub-answer, and refined sub-answer used to guide revision. "the triplet is called Socratic Feedback,"
- Socratic Self-Refine (SSR): A framework that decomposes reasoning into verifiable sub-steps, estimates step-level confidence, and iteratively refines errors. "In this paper, we propose Socratic Self-Refine (SSR), a novel framework for fine-grained evaluation and precise refinement of LLM reasoning."
- Socratic steps: Verifiable (sub-question, sub-answer) pairs extracted from a reasoning trace to enable step-level evaluation and correction. "SSR reformulates the reasoning process into a sequence of verifiable (sub-question, sub-answer) pairs, which we refer to as Socratic steps."
- Test-time scaling: Techniques that improve performance by parallel sampling and selection or confidence-driven refinement during inference. "which supports sample selection in our test-time scaling experiments~(\Secref{sec:experiments-tts})."
- Zero-shot prompting: Using prompts without task-specific training to elicit decomposition or verification directly from the LLM. "we adopt a zero-shot prompting approach with LLMs to decompose :"
Collections
Sign up for free to add this paper to one or more collections.