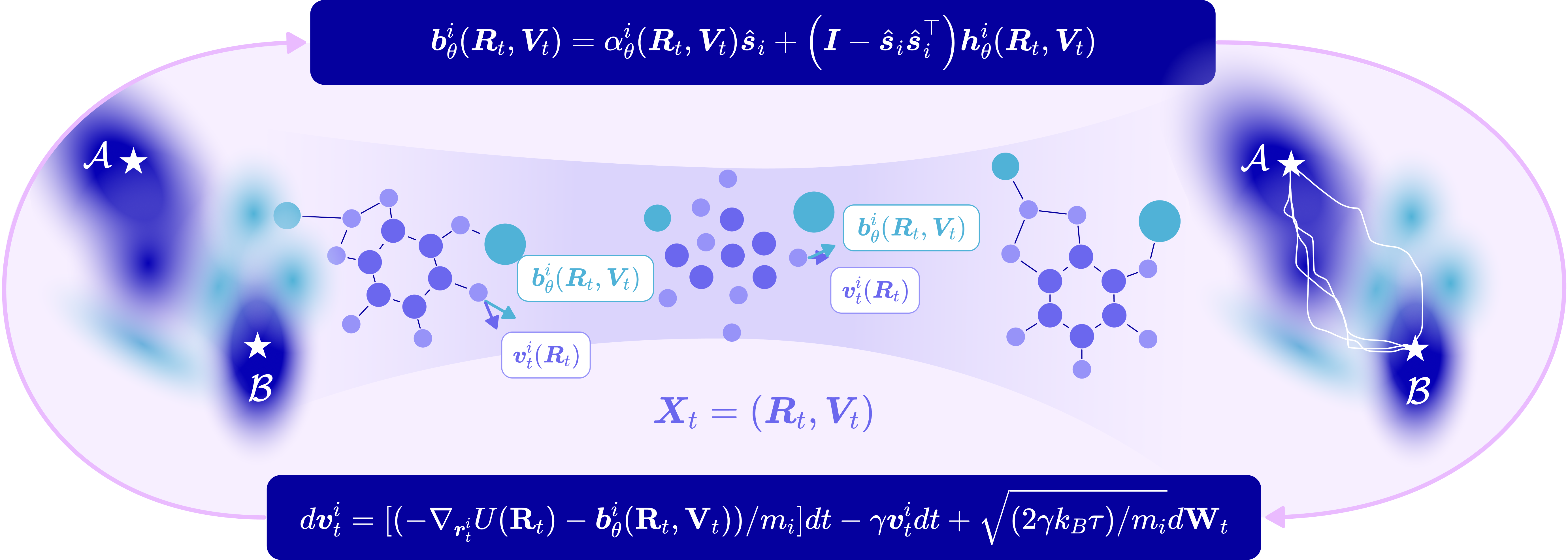
Entangled Schrödinger Bridge Matching (2511.07406v1)

Abstract: Simulating trajectories of multi-particle systems on complex energy landscapes is a central task in molecular dynamics (MD) and drug discovery, but remains challenging at scale due to computationally expensive and long simulations. Previous approaches leverage techniques such as flow or Schrödinger bridge matching to implicitly learn joint trajectories through data snapshots. However, many systems, including biomolecular systems and heterogeneous cell populations, undergo dynamic interactions that evolve over their trajectory and cannot be captured through static snapshots. To close this gap, we introduce Entangled Schrödinger Bridge Matching (EntangledSBM), a framework that learns the first- and second-order stochastic dynamics of interacting, multi-particle systems where the direction and magnitude of each particle's path depend dynamically on the paths of the other particles. We define the Entangled Schrödinger Bridge (EntangledSB) problem as solving a coupled system of bias forces that entangle particle velocities. We show that our framework accurately simulates heterogeneous cell populations under perturbations and rare transitions in high-dimensional biomolecular systems.

• The paper introduces a novel framework that uses entangled bias forces to simulate interacting multi-particle dynamics on complex energy landscapes.
• It leverages a Transformer-based architecture and stochastic optimal control to produce smooth, physically plausible trajectories with improved metrics like THP and RMSD.
• Empirical evaluations in molecular dynamics and cell perturbation modeling demonstrate robust generalization and superior performance compared to traditional SBM approaches.

Entangled Schrödinger Bridge Matching: Learning Interacting Multi-Particle Dynamics via Entangled Bias Forces

Introduction and Motivation

The Entangled Schrödinger Bridge Matching (EntangledSBM) framework is designed to simulate interacting multi-particle systems on complex and high-dimensional energy landscapes, addressing a critical gap in molecular dynamics (MD), drug discovery, and cell state modeling. Traditional Schrödinger Bridge Matching (SBM) and flow-matching approaches often assume homogeneous particle interactions, typically captured by mean-field or exchangeable paradigms, which are inadequate for heterogeneous systems where particle dynamics are dynamically entangled and dependent on evolving system-wide configurations. EntangledSBM formulates the problem as a coupled system governed by entangled bias forces that explicitly depend on the positions and velocities of all particles, providing a principled mechanism for learning second-order stochastic dynamics in multi-agent scenarios.

Figure 1: Schematic of EntangledSBM, demonstrating particle velocity entanglement and bias-force learning in multi-particle settings.

Theoretical Foundations and Framework

Langevin Dynamics and Schrödinger Bridges

EntangledSBM builds upon the foundation of Langevin dynamics, where each particle's evolution is dictated by both deterministic and stochastic terms, with velocities driven by conservative forces and stochastic environmental perturbations. Simulating trajectories from static snapshots is formalized under Schrödinger Bridge Matching, which seeks an optimal path distribution $\mathbb{P}^\star$ connecting initial and terminal distributions by minimizing the KL divergence between a bias-controlled dynamics and the optimal bridge distribution. The novelty of EntangledSBM is the introduction of bias forces $$\boldsymbol{b}_\theta(\boldsymbol{R}_t, \boldsymbol{V}_t)$$ which entangle the velocities across the system, thereby parameterizing non-factorizable, context-aware controls for each particle.

Entangled Schrödinger Bridge Problem and Optimal Control

EntangledSBM formalizes the entangled bridge matching problem as a stochastic optimal control (SOC) objective over coupled SDEs of the form:

$$d\boldsymbol{r}^i_t = \frac{1}{\gamma}(-\nabla_{\boldsymbol{r}^i_t}U(\boldsymbol{R}_t) + \boldsymbol{b}^i(\boldsymbol{R}_t, \boldsymbol{V}_t))\,dt + \sqrt{\frac{2 k_B \tau}{\gamma}} d\boldsymbol{W}^i_t$$

where the bias forces $\boldsymbol{b}^i$ are functions of both positions and velocities of all particles. The SOC objective minimizes expected quadratic bias norm and maximizes the log-probability under the target terminal state. The problem is solved via convex importance-weighted cross-entropy objectives, enabling efficient off-policy learning and replay-buffer-based trajectory optimization.

Methodological Innovations

Parameterization of Bias Forces

EntangledSBM features a bias force decomposition with a parallel directional component (towards the target distribution gradient) and an orthogonal flexibility component:

$$\boldsymbol{b}_\theta^i(\boldsymbol{R}_t,\boldsymbol{V}_t) = \alpha^i_\theta(\cdots)\hat{\boldsymbol{s}}_i + (\boldsymbol{I} - \hat{\boldsymbol{s}}_i\hat{\boldsymbol{s}}_i^\top)\boldsymbol{h}_\theta^i(\cdots)$$

where $\hat{\boldsymbol{s}}_i$ is normalized direction to the target, $\alpha^i_\theta$ is a learned non-negative scale via softplus, and $\boldsymbol{h}_\theta^i$ enables nontrivial movement orthogonal to the optimal transport direction. This ensures the distance to the target distribution is non-increasing during simulation, while preserving expressive trajectory routing around constraints or energetic barriers.

Transformer-Based Architecture

Particle dependencies are modeled using Transformer encoders, where concatenated position-velocity features for all $n$ particles attend globally in the system and can be conditioned on arbitrary target distributions. For MD, Kabsch alignment is applied to maintain geometric invariance. The architecture supports direct generalization to unseen targets at inference, an essential property for realistic perturbation and sampling tasks.

Applications and Empirical Evaluation

Cell Cluster Dynamics under Drug Perturbation

EntangledSBM is evaluated on cell state modeling tasks using the Tahoe-100M dataset, leveraging principal component projections of high-dimensional gene expression data. Compared to baselines that lack velocity conditioning or use static objectives, EntangledSBM significantly decreases RBF-MMD and Wasserstein distances in reconstructing both trained and unseen target populations. A strong empirical result is the model's capability to generalize to unseen clusters with minimal performance degradation, supporting biological relevance for large-scale, sparse data scenarios.

Figure 2: Visualization of cell cluster trajectories under Clonidine perturbation, comparing effects of base, unconditioned, log-variance, and cross-entropy objectives across 150 PCs.

Figure 3: Comparative impact of velocity conditioning in EntangledSBM trajectories for Trametinib cell perturbation, highlighting superiority of CE-trained models for both trained and novel targets.

Transition Path Sampling in Molecular Dynamics

EntangledSBM is tested on protein folding tasks with both small molecules (Alanine Dipeptide) and larger fast-folding proteins (Chignolin, Trp-cage, BBA) at all-atom resolution. Model outputs are quantitatively evaluated by RMSD, Target Hit Percentage, and Energy of Transition States, with EntangledSBM consistently outperforming established benchmarks such as Path Integral Path Sampling and TPS-DPS. Notably, EntangledSBM achieves higher THP and lower RMSD for target hits in both small and large-scale biomolecular settings.

Figure 4: Transition paths on energy landscapes for Alanine Dipeptide and fast-folding proteins, illustrating simulated pathways and successful target conformations.

Design Choices, Trade-offs, and Implications

Cross-Entropy versus Log-Variance Divergence

Empirical analysis shows the cross-entropy objective yields smoother, more physically plausible trajectories through intermediate states, while the log-variance divergence can result in abrupt or unrealistic transitions. The cross-entropy's convexity in the path measure ensures unique minimizers and stable training dynamics even under off-policy supervision, which is critical for sample efficiency with a replay buffer.

Generalization to Unseen Targets

EntangledSBM's conditioning on target distribution direction and global particle dependencies allow superior generalization to novel objectives, addressing common weaknesses in SBM and flow-matching strategies where explicit retraining or manual feature engineering is required for each new target.

Computational and Practical Considerations

The entangled bias force and Transformer architecture scale well to moderate $n$ but will encounter resource constraints as system size increases (e.g., full atomistic simulations of large proteins or cell populations above $10^4$ agents). The use of a replay buffer for off-policy learning partially alleviates simulation costs. The model's ability to integrate with physical simulation engines (OpenMM for MD, direct PCA manipulation for gene-expression data) supports practical deployment in both biological and chemical domains.

Limitations and Future Directions

Current validation is restricted to specific perturbation classes and fast-folding proteins. Extension to larger biomolecular complexes, broader cell perturbation modalities (genetic, environmental), and different particle-based systems in physics are immediate directions. The model's integration with experimentally derived potentials or single-cell multiomics remains unexplored. The theoretical framework opens opportunities for meta-learning strategies in multi-agent systems, improved uncertainty quantification in high-dimensional path sampling, and the use of more expressive context-aware architectures.

Conclusion

EntangledSBM introduces a rigorously grounded mechanism for learning the stochastic dynamics of interacting multi-particle systems, parameterizing entangled bias forces via neural architectures, and optimizing via cross-entropy objectives in path space. The framework sets state-of-the-art performance benchmarks in both cell perturbation modeling and transition path sampling for molecular systems, demonstrating robust generalization to novel distributions and trajectories. Its theoretical and empirical advances are relevant not only to biophysical and cellular modeling but to general-purpose modeling of entangled, heterogeneous agent systems in science and engineering.