Transformers Provably Learn Chain-of-Thought Reasoning with Length Generalization (2511.07378v1)
Abstract: The ability to reason lies at the core of AI, and challenging problems usually call for deeper and longer reasoning to tackle. A crucial question about AI reasoning is whether models can extrapolate learned reasoning patterns to solve harder tasks with longer chain-of-thought (CoT). In this work, we present a theoretical analysis of transformers learning on synthetic state-tracking tasks with gradient descent. We mathematically prove how the algebraic structure of state-tracking problems governs the degree of extrapolation of the learned CoT. Specifically, our theory characterizes the length generalization of transformers through the mechanism of attention concentration, linking the retrieval robustness of the attention layer to the state-tracking task structure of long-context reasoning. Moreover, for transformers with limited reasoning length, we prove that a recursive self-training scheme can progressively extend the range of solvable problem lengths. To our knowledge, we provide the first optimization guarantee that constant-depth transformers provably learn $\mathsf{NC}1$-complete problems with CoT, significantly going beyond prior art confined in $\mathsf{TC}0$, unless the widely held conjecture $\mathsf{TC}0 \neq \mathsf{NC}1$ fails. Finally, we present a broad set of experiments supporting our theoretical results, confirming the length generalization behaviors and the mechanism of attention concentration.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Transformers Provably Learn Chain-of-Thought Reasoning with Length Generalization — Explained Simply
Overview
This paper studies whether a kind of AI called a transformer can truly learn “chain-of-thought” (step-by-step) reasoning and keep working well on longer, harder problems than it was trained on. The authors build a simple, clean test to analyze this and prove, with math, when and why transformers can learn to reason and generalize to longer sequences. They also show a way for the model to teach itself to handle even longer problems over time.
Key Questions
The paper focuses on two easy-to-understand questions:
- Can transformers trained with standard methods learn genuine step-by-step reasoning, not just simple tricks?
- After learning on short problems, can the same model solve longer versions of those problems without being retrained on long ones?
How They Studied It
Think of the task as tracking the state of a game as you apply moves:
- You start with an initial state (like a number or a board position).
- You apply a sequence of actions or moves.
- The goal is to predict the state after each move and especially the final state.
The authors use a synthetic (made-up but controlled) task called “LEGO.” It’s like a list of small instructions, each line describing either:
- A relationship between two variables through an action (a “predicate”), or
- The actual value of a variable at a certain point (an “answer”).
To avoid overload, here’s the main setup in everyday terms:
- Transformer: A popular AI model that uses “attention” to focus on the most relevant parts of the input, like a spotlight scanning a page for the facts it needs.
- Attention: A scoring mechanism that says “this line in the input matters a lot for the current prediction.”
- Chain-of-thought (CoT): The model produces intermediate steps (like scratch work in math) before the final answer.
- Gradient descent: A standard training method where the model slowly adjusts its internal knobs to reduce mistakes.
- Length generalization: Learning from short examples but being able to solve longer ones.
They analyze two kinds of action structures:
- Simply transitive actions: There’s a unique move that takes you from any state to any other state. A helpful mental picture is a circular board where one unique rotation always lands you on the target spot.
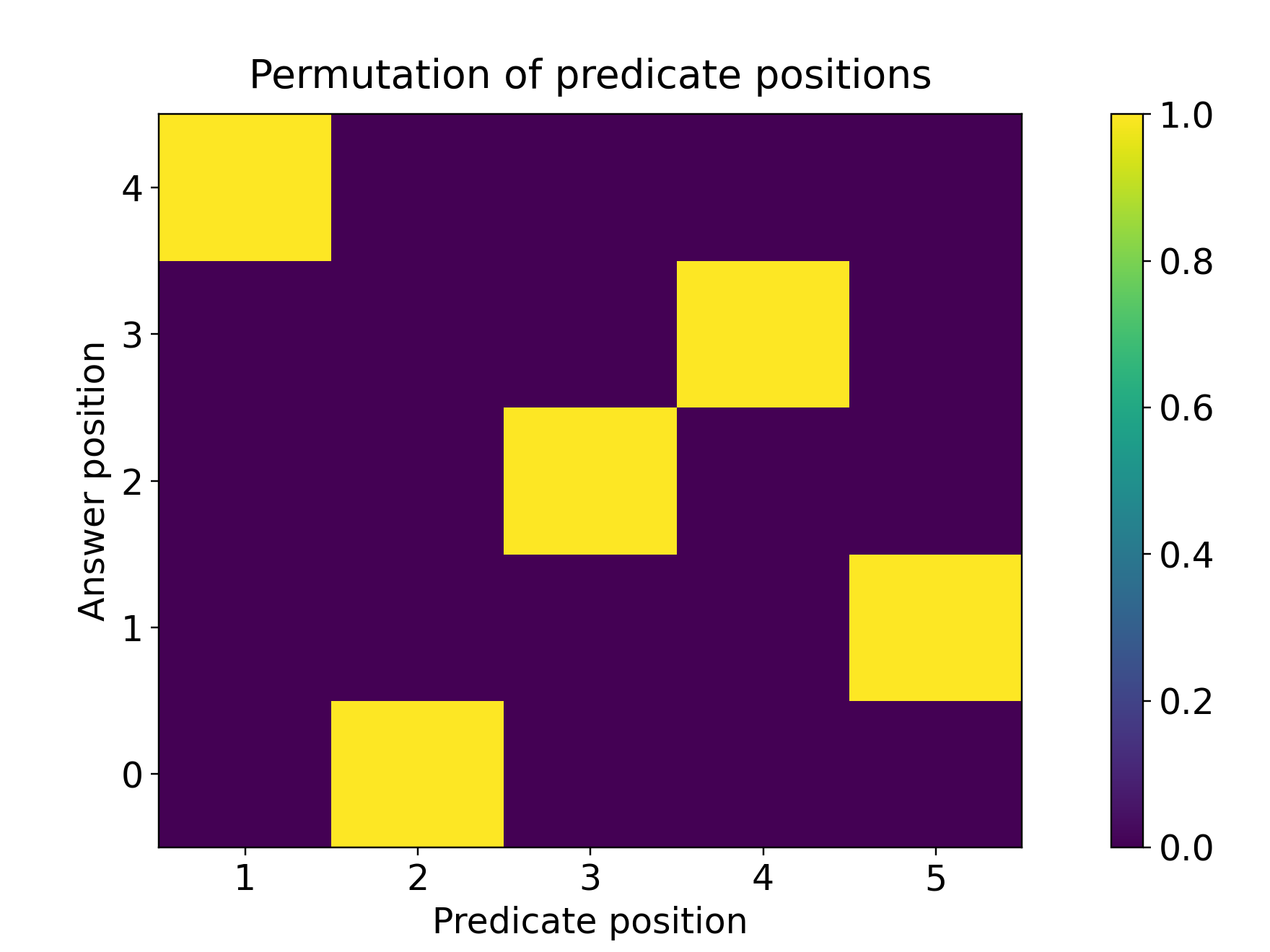
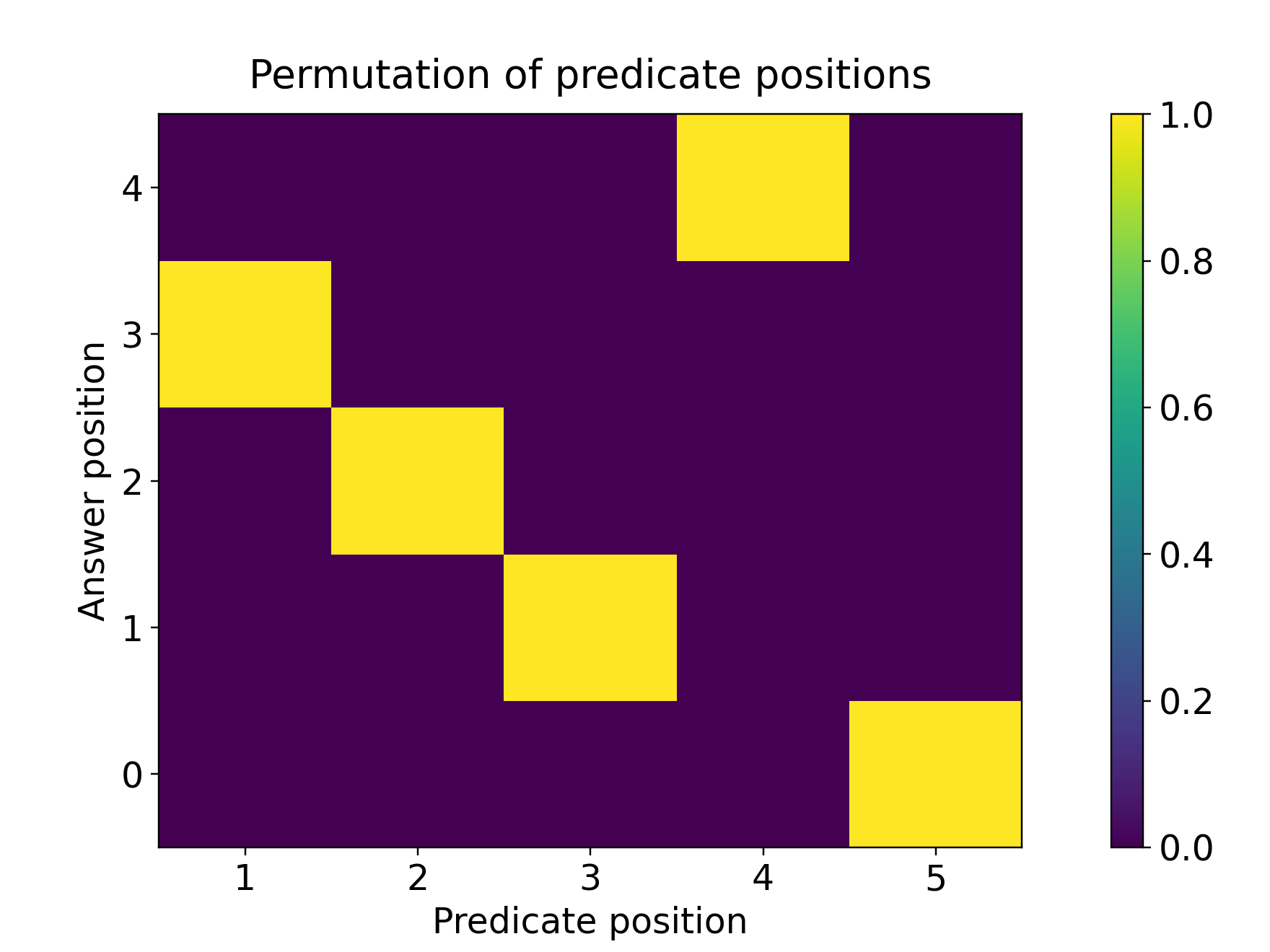
- Symmetry actions (like the permutation group Sₙ): There are many different moves that can send one state to another (think shuffling cards—many shuffles can take Ace to the top). This creates “distractors,” making attention focusing harder.
To train step-by-step reasoning, they use teacher forcing: the model is given correct earlier answers and is trained to predict the next one. They also try a simple two-stage curriculum (first learn one-step reasoning, then two-step), and a recursive self-training method where the model trains on its own longer reasoning traces to push its limits further.
What They Found and Why It Matters
Here are the main results, explained with minimal math:
- Transformers do learn chain-of-thought on these state-tracking tasks.
- They provide a mathematical proof that a one-layer transformer trained with gradient descent can learn to track states using CoT and make correct predictions step-by-step.
- Length generalization depends on the action structure.
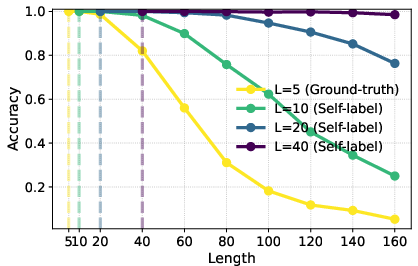
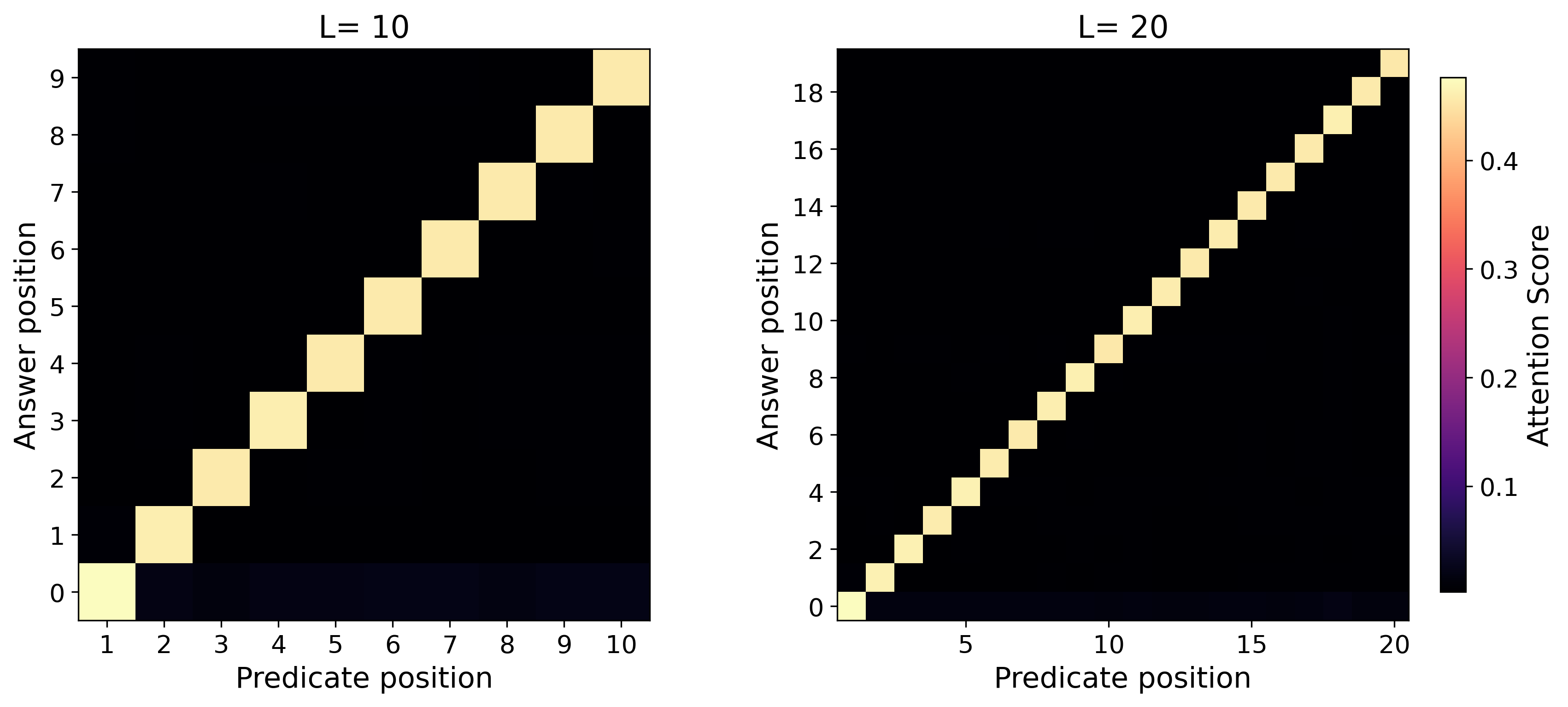
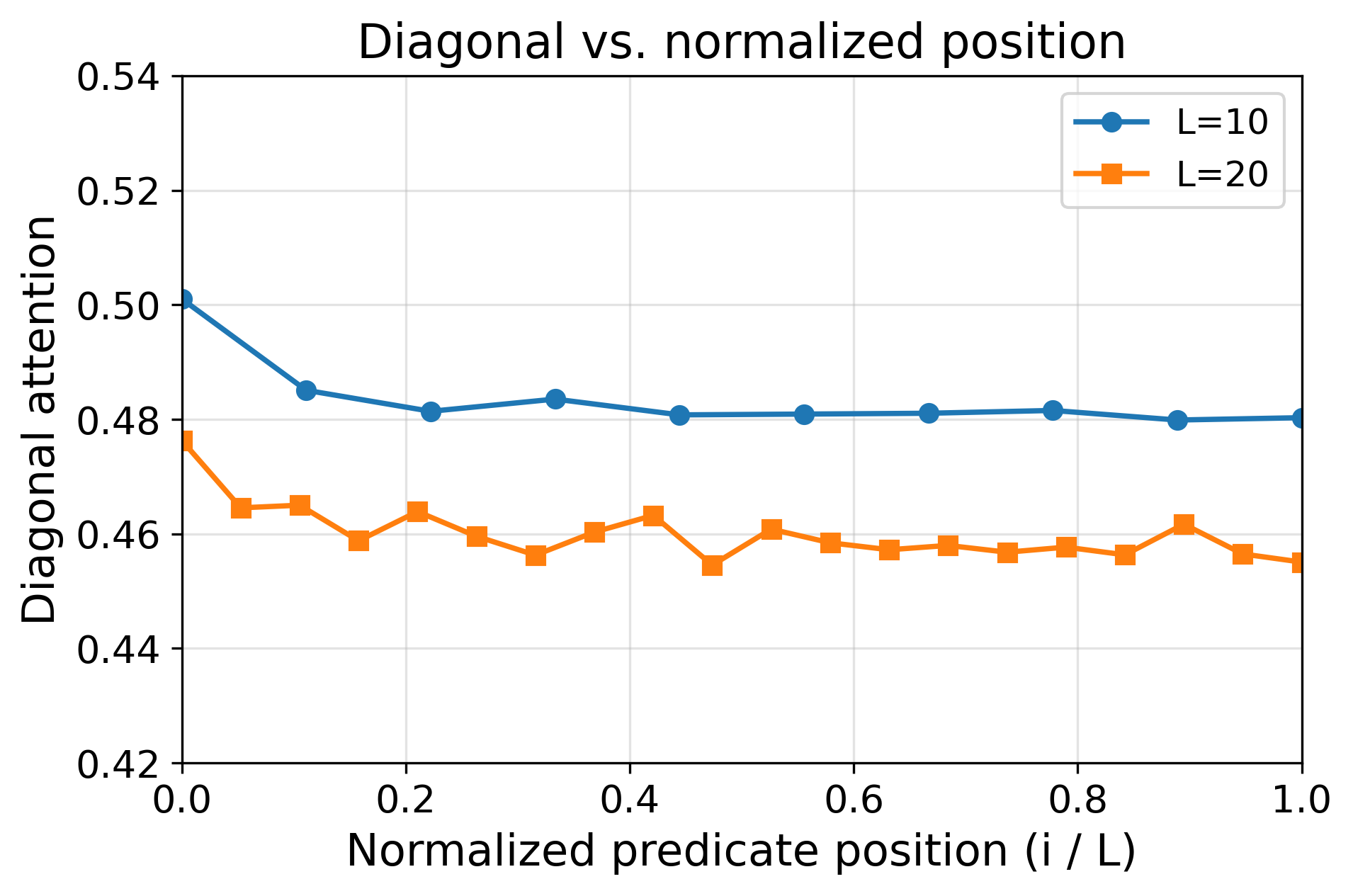
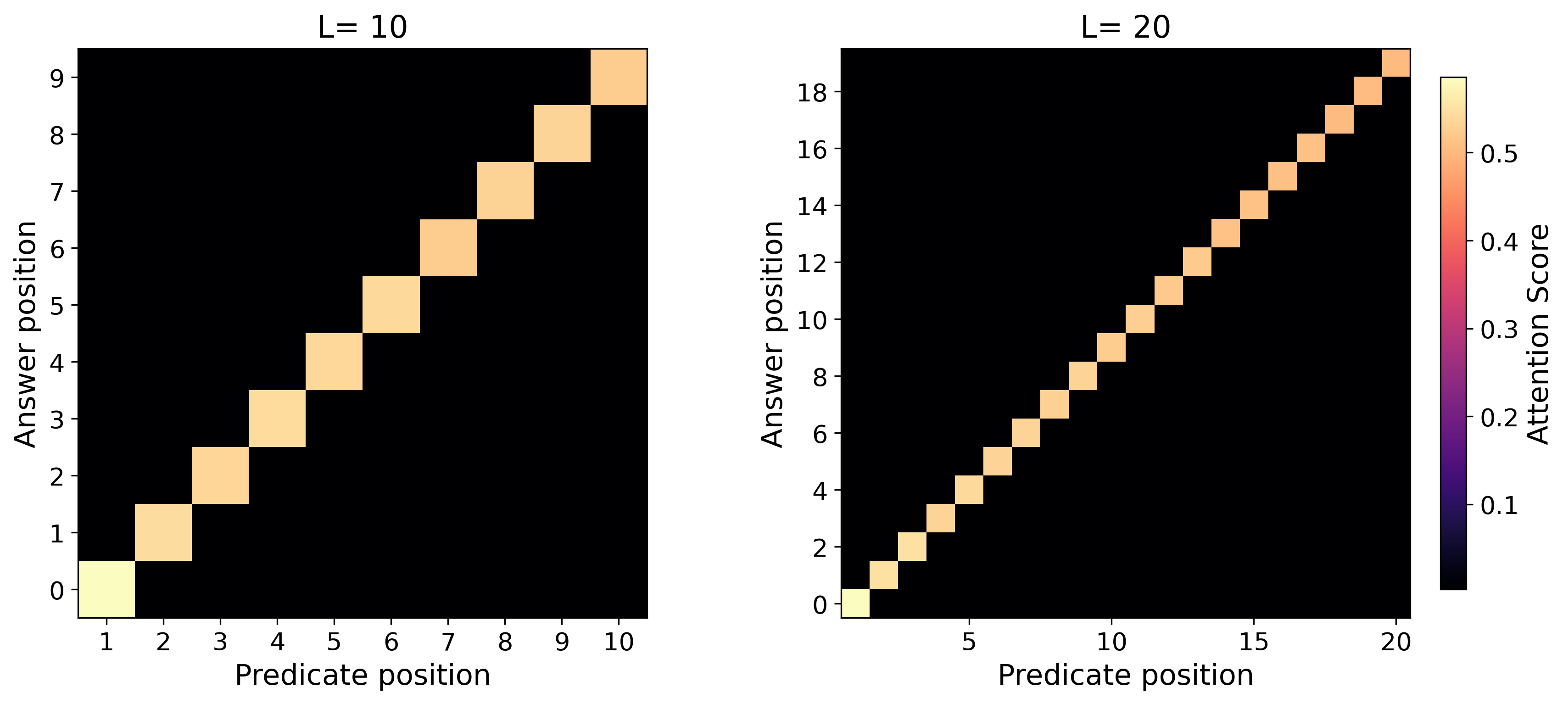
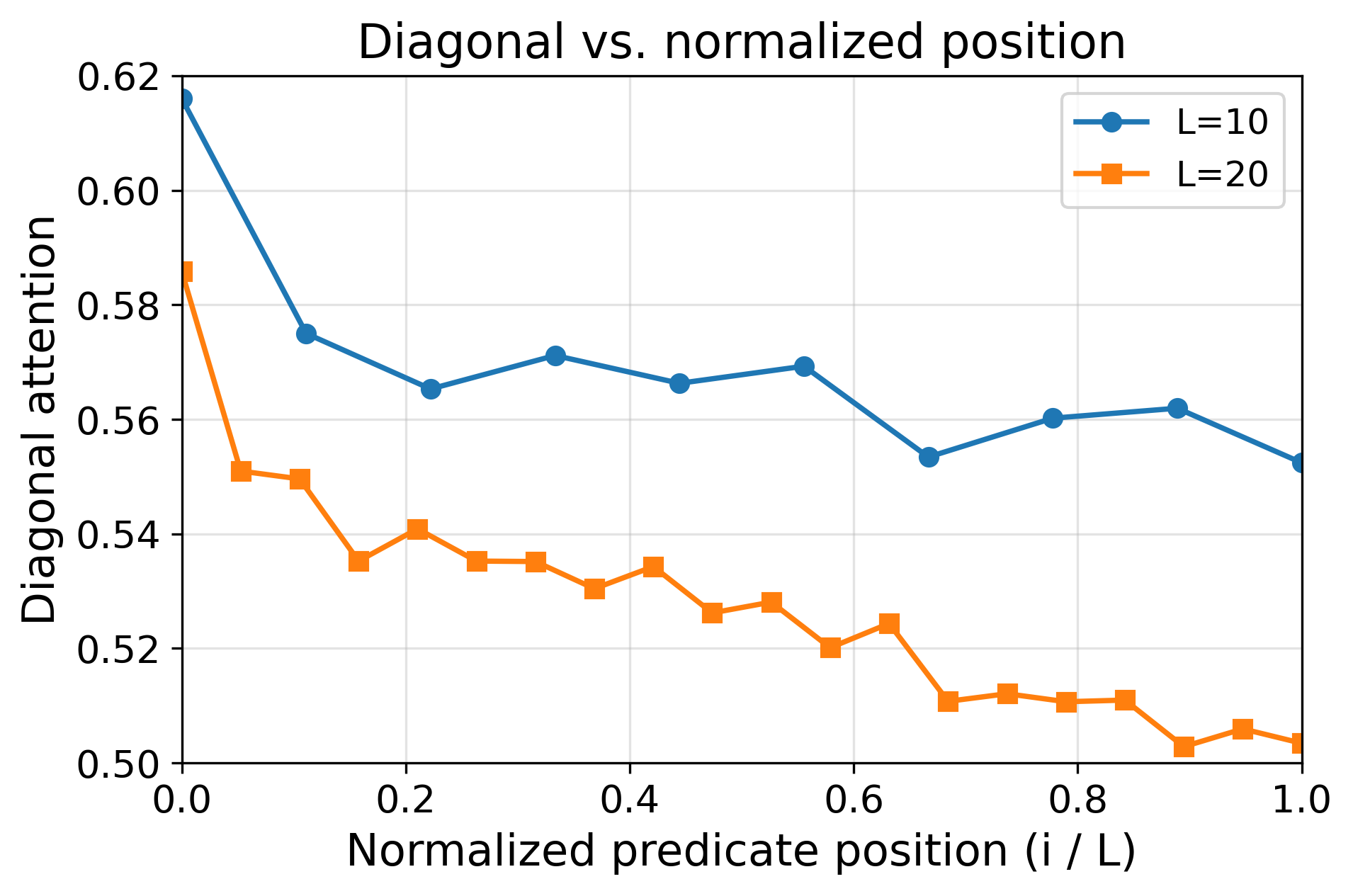
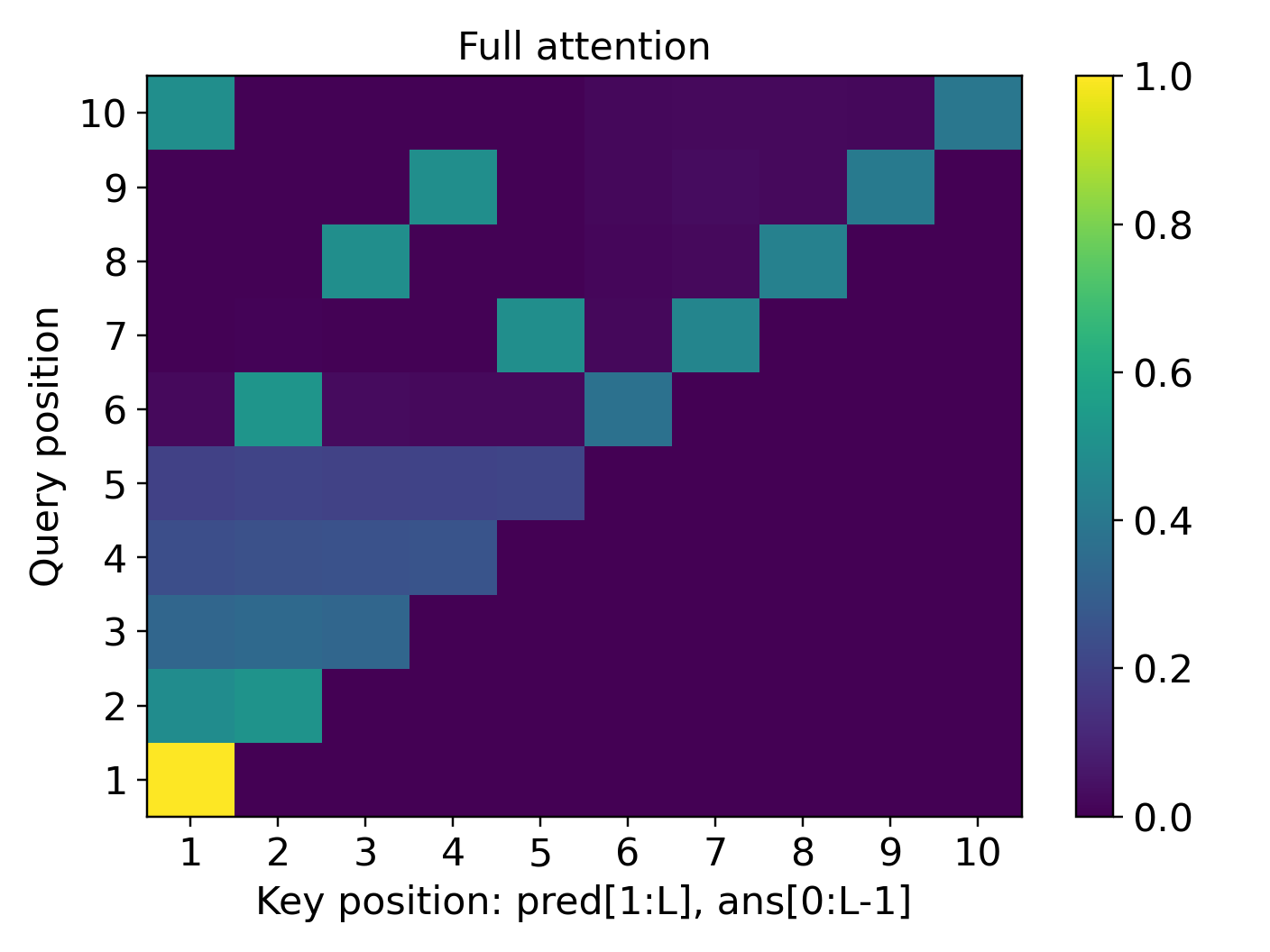
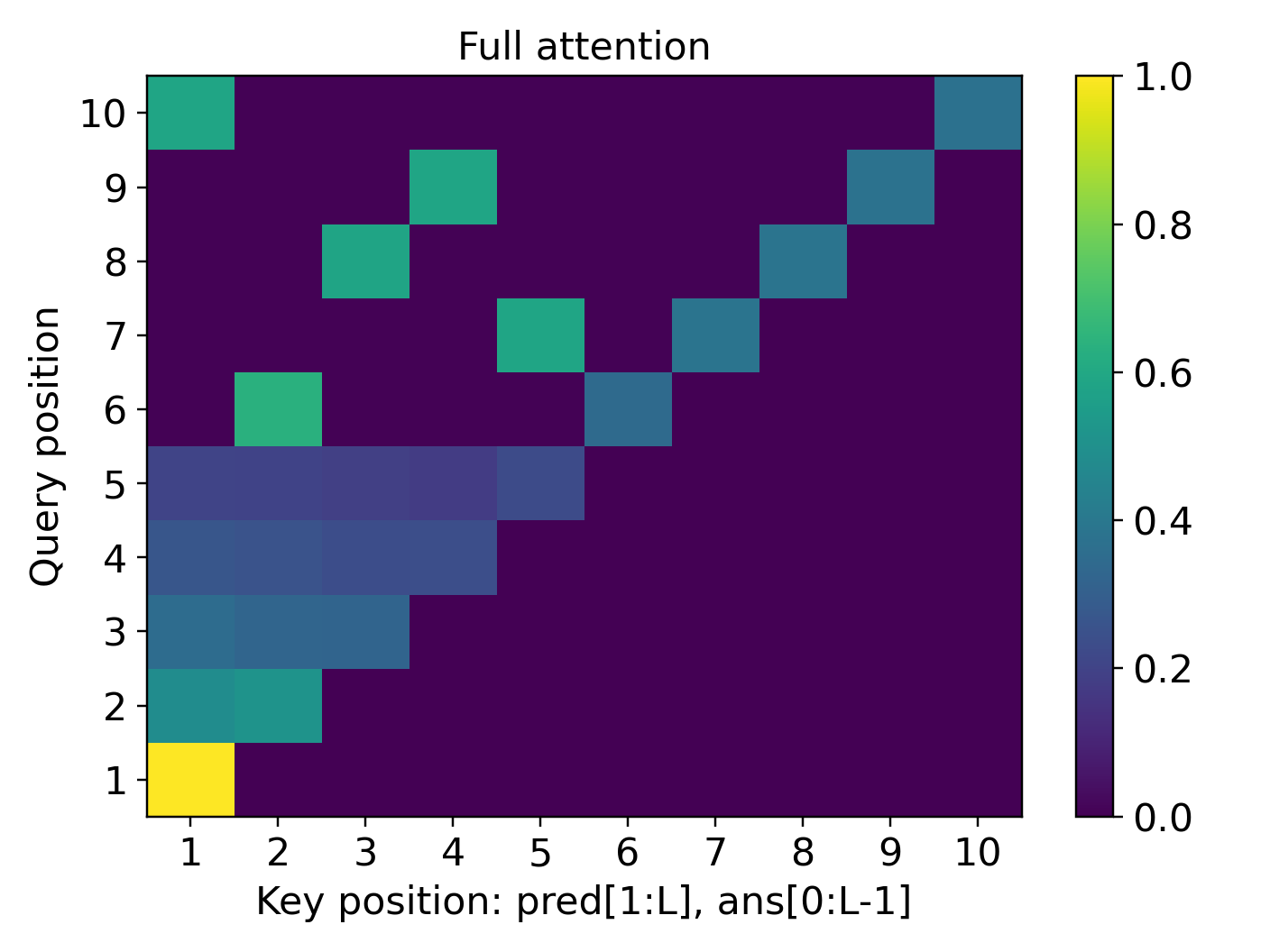
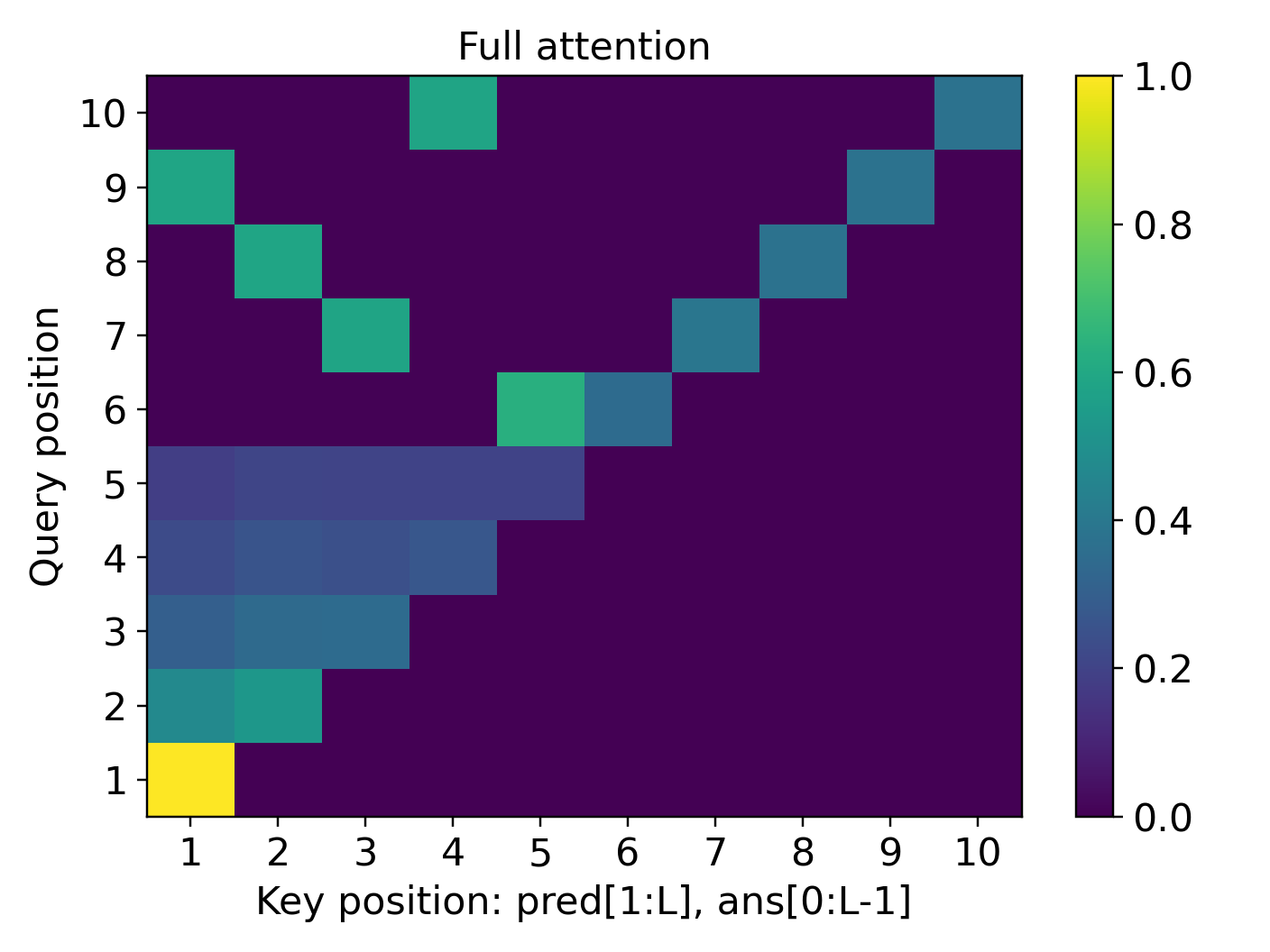
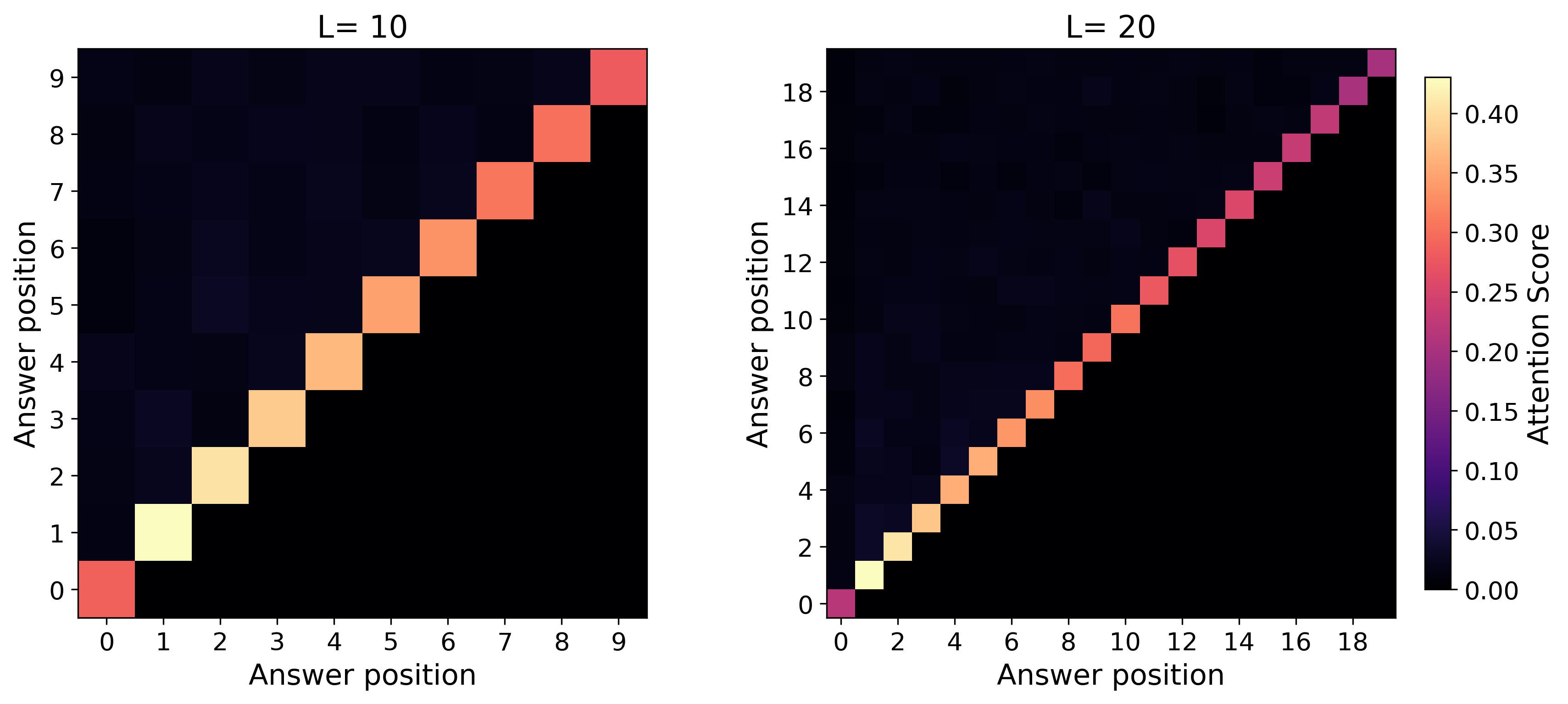
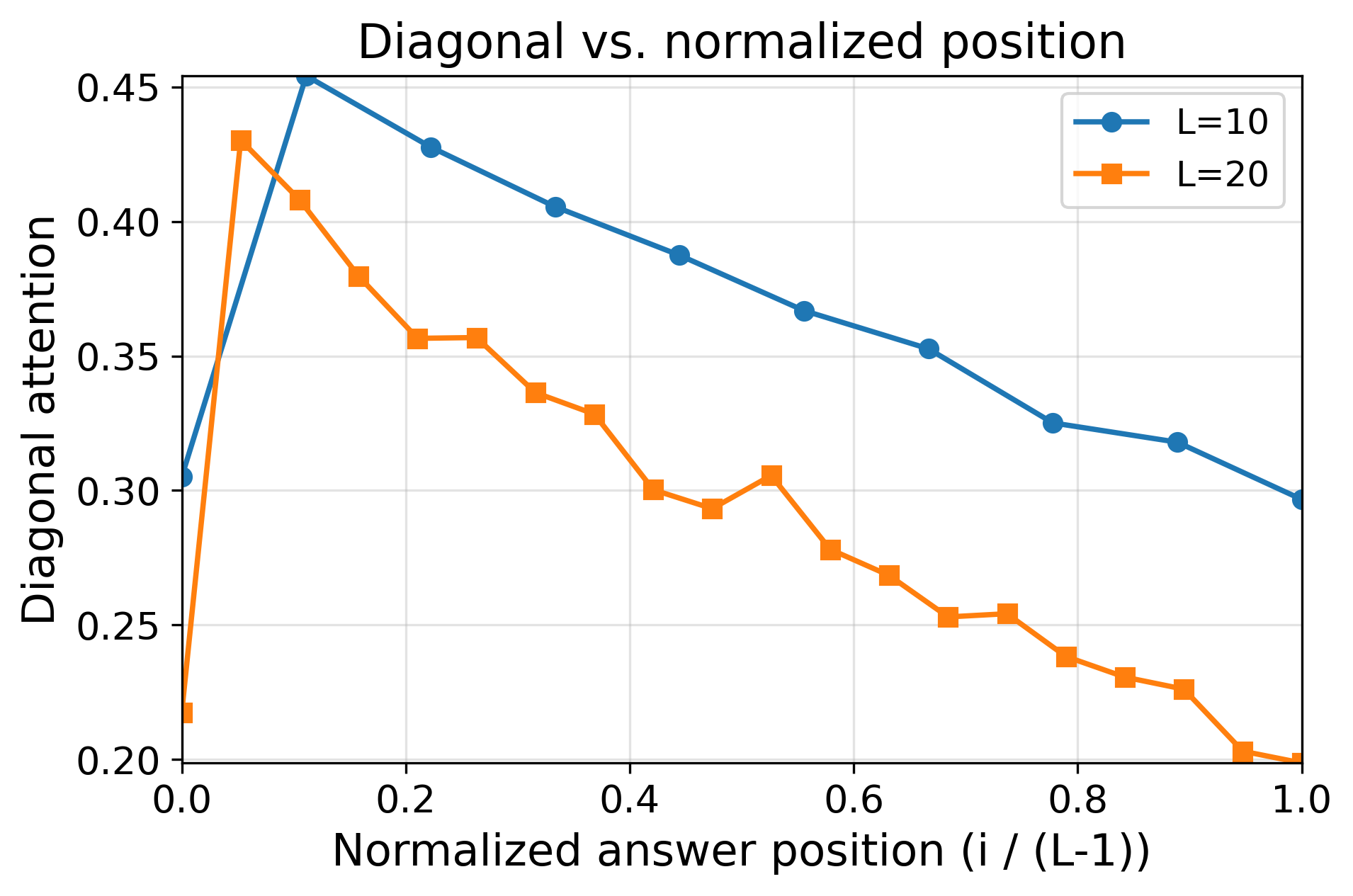
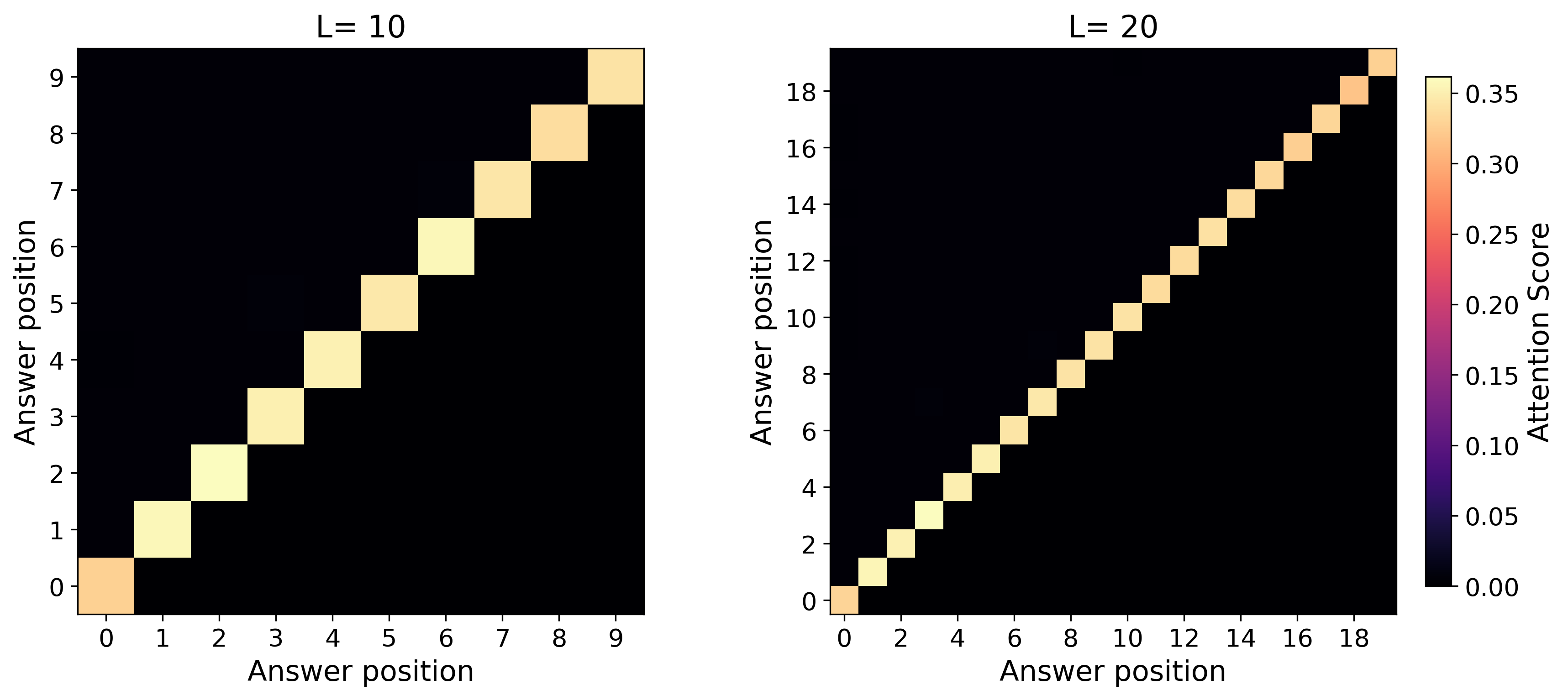
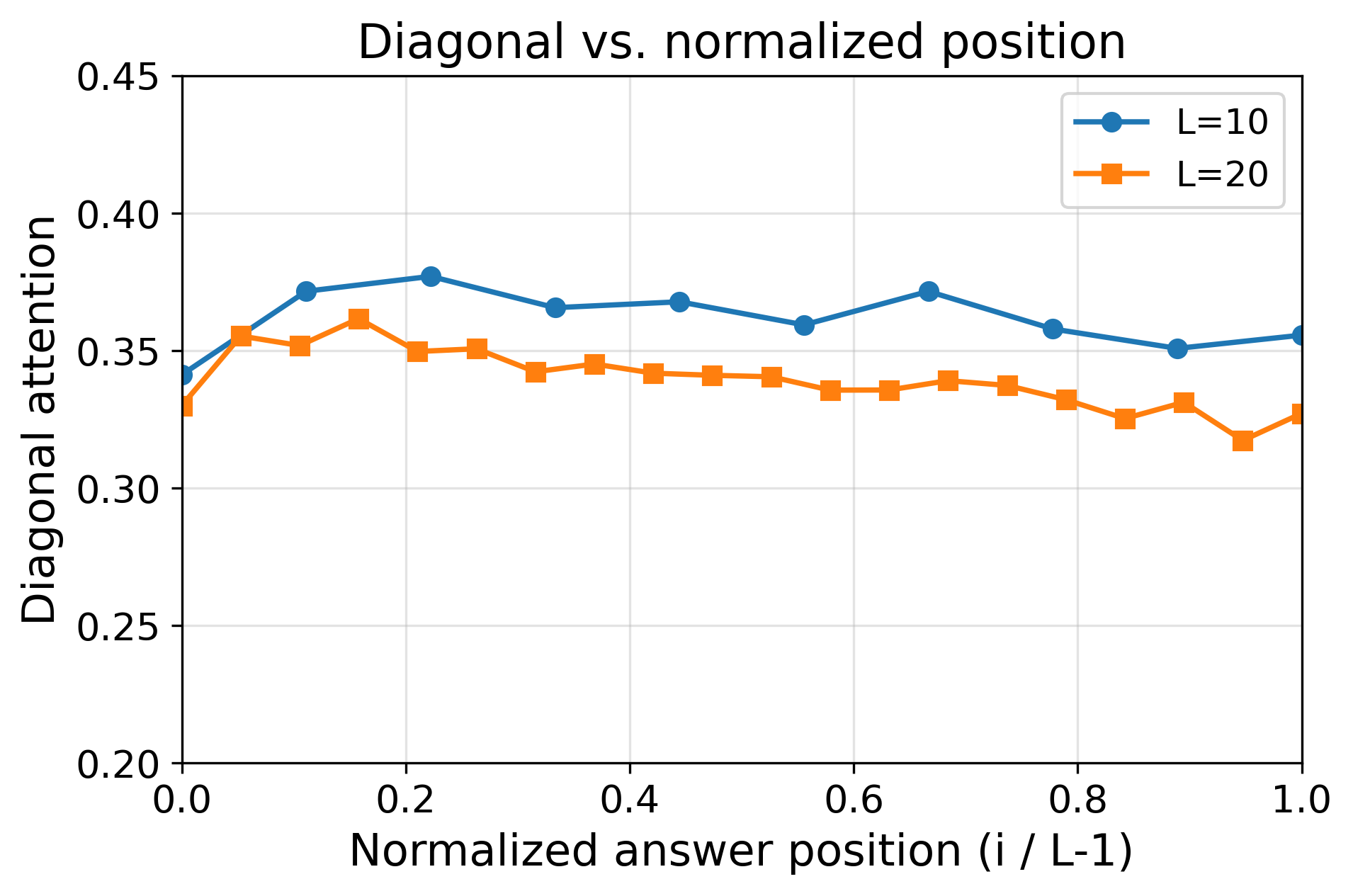
- For simply transitive actions (the “clean, one-unique-move” setting), the learned reasoning generalizes to much longer problems than seen during training. The model’s attention forms a sharp, reliable focus (“attention concentration”) on exactly the lines it needs, even as the input gets longer.
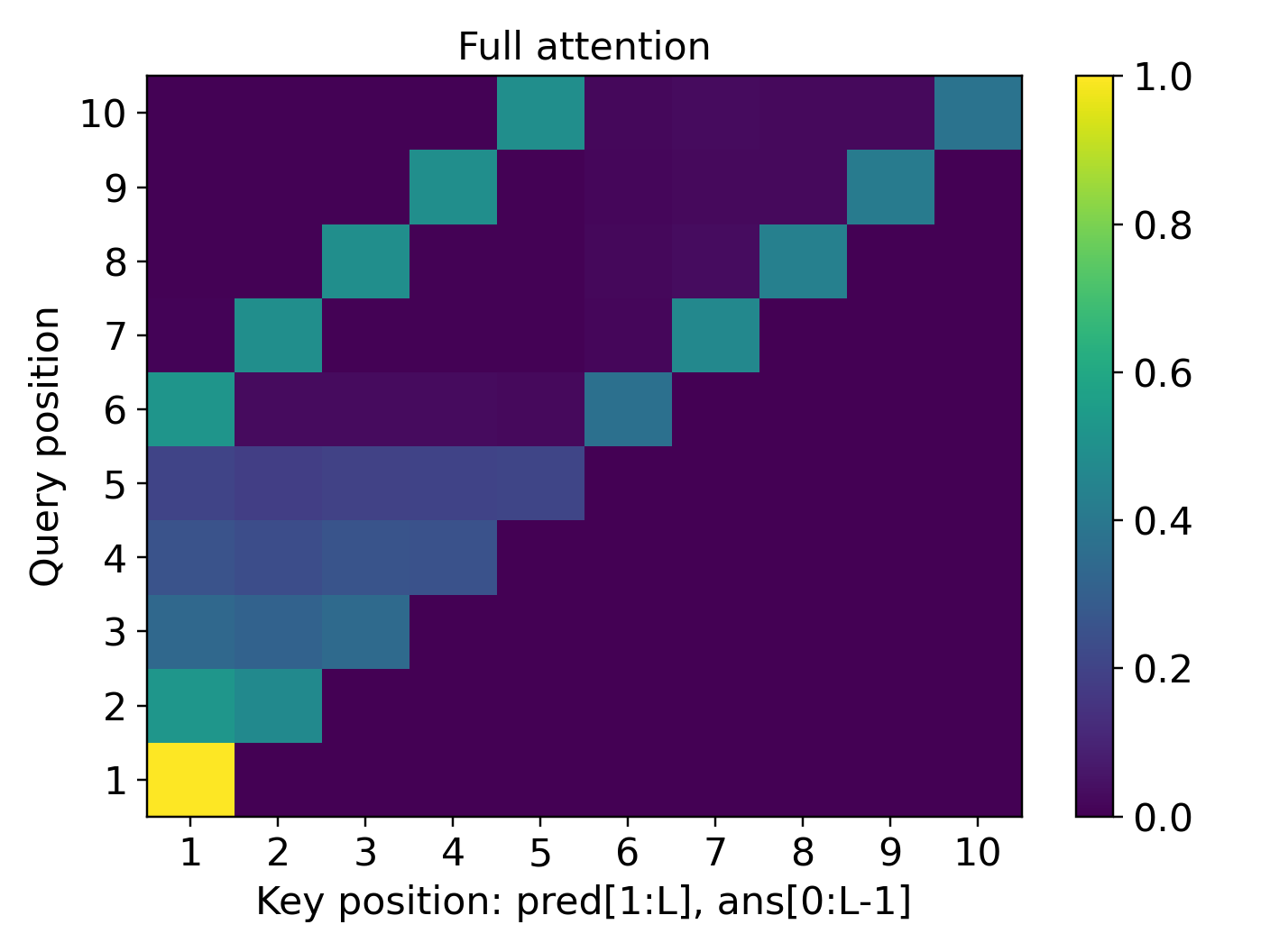
- For symmetry actions (the “many possible moves” setting), the model generalizes only a little beyond the training length. Because many lines in the input look similarly relevant, the attention becomes diluted—its spotlight is less focused—so long sequences confuse it.
- A self-training strategy extends the model’s reach.
- When direct generalization falls short (as in symmetry actions), training the model on its own longer chains helps it progressively handle longer problems. Each round trains on longer traces, so it keeps leveling up until it reaches the maximum length allowed in the setup.
- Theoretical significance: beyond “shallow” problem classes.
- In computer science, problem difficulty is sometimes described by circuit complexity classes. The authors show their trained transformer can solve problems believed to require deeper, more sequential reasoning (called NC¹) rather than only shallow, highly parallel problems (called TC⁰). This gives the first training-time guarantee (not just “in theory it can represent it”) that a constant-depth transformer can learn tasks beyond TC⁰ if it uses CoT.
The authors back these points with experiments that match the proofs:
- Simply transitive tasks generalize to much longer sequences reliably.
- Symmetry tasks only generalize a bit unless self-training is added.
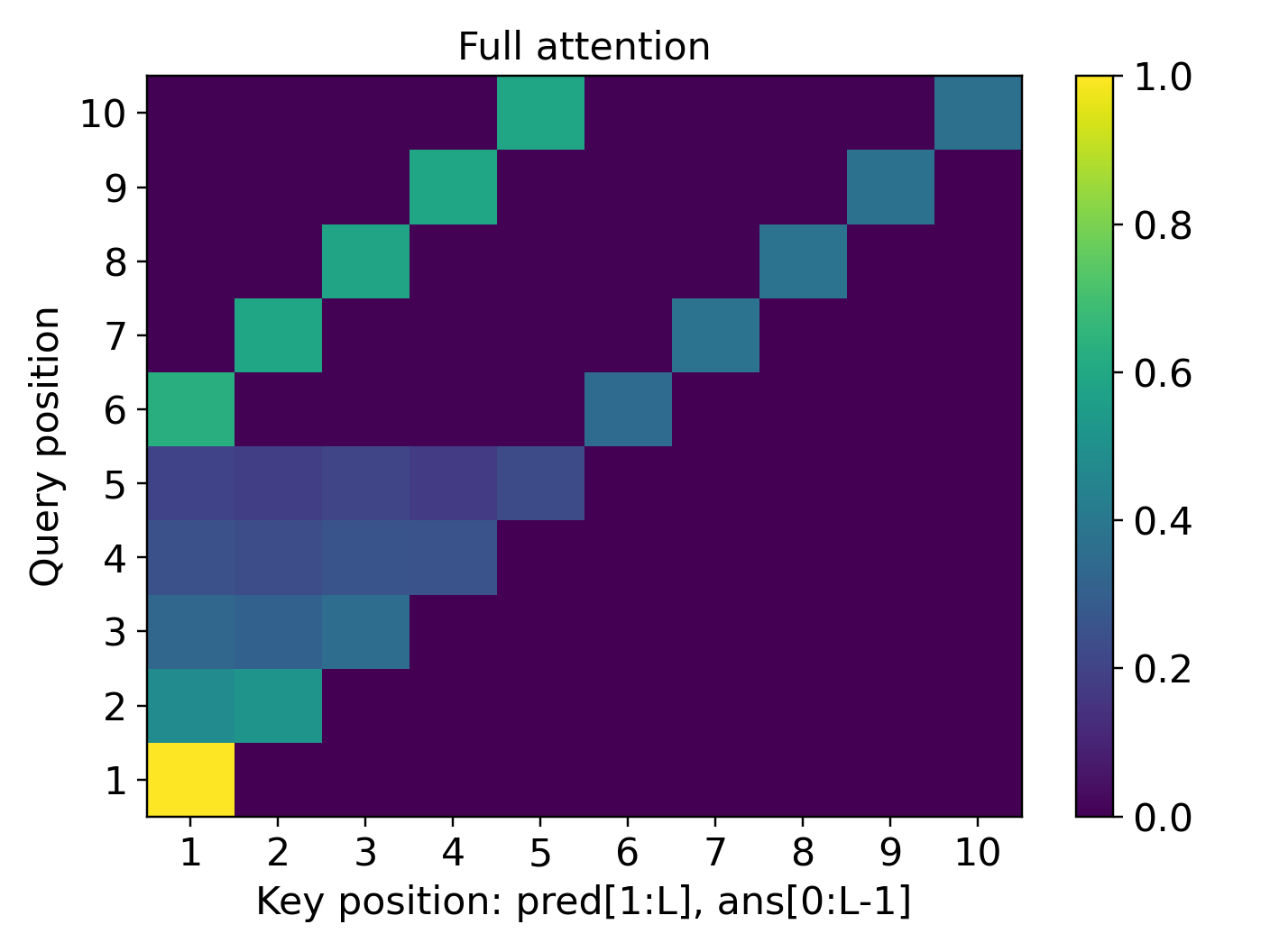
- Attention heatmaps show the “attention concentration” pattern: the model strongly focuses on two key lines at each step (the current answer and the needed predicate), especially in the simply transitive case.
Why This Is Important
This work gives a clearer picture of how and when transformers really learn reasoning, not just pattern-matching. It shows:
- Structure matters: If your problem’s rules make it easy for the model to focus on the right lines, it will scale to longer contexts more reliably.
- Training matters: Even simple curricula and self-training can boost reasoning length.
- Theory meets practice: It’s not just that transformers can represent complex reasoning; they can actually learn it with standard training.
These insights can guide building better reasoning models in the real world:
- Choose or design tasks (and training data) that encourage sharp attention focus.
- Use self-training or curricula to extend a model’s reasoning length.
- Understand limits: Some tasks need extra help (like self-training) to generalize well.
In Short
- The paper proves that transformers can learn step-by-step reasoning on structured tasks.
- It explains why some tasks generalize to much longer lengths and others don’t.
- It introduces a simple self-training method to push the model to solve longer problems.
- It bridges practical training with deeper theory, showing learned CoT can tackle problems thought to need more sequential computation.
Overall, this research helps us understand and improve how AI reasons, especially when problems get long and complex.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of what remains missing, uncertain, or unexplored in the paper, structured to enable concrete follow-up research.
- Architectural generality: Results are proved for a one-layer transformer with NoPE, single (folded) attention scoring matrix, no residual connections, no layer norm, and a custom sReLU activation. It is unknown whether the attention-concentration mechanism and length generalization guarantees persist for standard multi-layer, multi-head transformers with residuals, layer norm, GELU, and typical query/key/value parameterization.
- Positional encoding dependence: The entire theory assumes no positional encoding (NoPE). Whether the same learning and generalization behavior holds (or improves/degrades) under commonly used encodings (e.g., RoPE, ALiBi, learned absolute/relative) is unaddressed.
- Block-sparse attention restriction: The analysis imposes a fixed block-sparsity pattern on the attention matrix (only blocks (4,3) and (4,4) are trainable). It is unknown if the guarantees hold with fully dense attention or different sparsity patterns; moreover, the role of multi-head attention as a potential remedy for distractors isn’t analyzed.
- Activation and clipping assumptions: Proofs rely on a bespoke smooth ReLU and coordinate-wise logit clipping. It is unclear whether the results extend to standard activations (ReLU/GELU) and without logit clipping, or how sensitive the guarantees are to these choices.
- Orthogonality of embeddings: The theory assumes orthonormal token embeddings and a zero vector for the blank token. Robustness to realistic, learned, non-orthogonal embeddings (or pretrained embeddings) and the impact on attention concentration are not studied.
- Optimization algorithm mismatch: Guarantees are derived for full-batch gradient descent with fixed step sizes. The behavior under practical optimizers (Adam/AdamW, SGD with momentum), learning-rate schedules, and stochastic mini-batching lacks theoretical and empirical validation.
- Sample complexity and convergence rates: The paper does not quantify the number of training samples and gradient steps required to reach the regimes where attention concentration and length generalization occur, nor does it provide convergence rates or computational complexity bounds.
- Teacher forcing vs free-running inference: Training uses next-clause loss with ground-truth previous answers. The paper does not analyze error propagation when the model conditions on its own (possibly imperfect) generated CoT steps at inference, nor provide bounds relating training-time accuracy to end-to-end free-running performance.
- Distributional assumptions and robustness: LEGO sequences are generated with uniformly random variables (without replacement), uniformly random actions, and clean, consistent clauses. Sensitivity to repeated variables, skewed action distributions, noisy/contradictory clauses, distractor tokens, or spurious correlations is unknown.
- Generality beyond two action families: The results qualitatively separate simply transitive actions from symmetry actions, but do not characterize length generalization as a function of stabilizer sizes or other group-theoretic properties. A general theory linking stabilizer structure (e.g., its size or entropy) to achievable length generalization is missing.
- Scaling of group size: Assumption |G| ≤ log{C0} d conflicts with large groups (e.g., S_n grows as n!). The conditions under which NC1-complete symmetry tasks remain within the paper’s asymptotic regime, and how guarantees scale when |G| grows polynomially or exponentially with d, are not clarified.
- Maximum allowable length: Several claims reference a “maximal allowable length d.” The rationale for this cap and how length generalization behaves beyond that bound (or under different scaling regimes linking L to d) is not theoretically justified.
- Self-training robustness: The recursive self-training guarantee assumes self-labeled traces of increasing length are sufficiently accurate. The impact of noisy or partially incorrect self-generated traces, criteria for trace selection/filtering, and failure modes (e.g., compounding errors) are not analyzed.
- Curriculum design details: The proofs hinge on a specific staged curriculum (e.g., T1, T2 updates, double-and-self-label schedule). How sensitive the outcomes are to curriculum hyperparameters, alternative schedules (e.g., gradual rather than doubling), or mixed-length training is unstudied.
- Attention concentration quantification: While attention heatmaps show concentration, the theory does not provide quantitative bounds (e.g., margin or temperature-like parameters) linking concentration levels to accuracy or extrapolation length, nor robustness to distractor density.
- Efficiency trade-offs: CoT achieves NC1-like expressivity via serial computation, but the paper does not analyze computational/memory costs at inference (e.g., time per CoT token, peak memory with long contexts) or compare against parallel alternatives and memory-augmented architectures.
- Extension beyond LEGO: It is unclear whether the mechanisms and guarantees transfer to more realistic reasoning datasets (code execution, mathematical proofs, multi-step tool use) with natural language variability, longer clauses, and richer syntax.
- Token-level vs clause-level modeling: The model predicts 5-token clauses as unified units. How the results translate to standard token-by-token next-token prediction (with variable-length tokens and subword units) remains open.
- Empirical coverage and statistical rigor: Experiments are limited to synthetic tasks with few architecture choices; broader ablations (width m, number of neurons, learning rates, seeds), statistical significance, and error bars are not presented, leaving uncertainty about robustness.
- Formal constant specifications: Informal theorems reference constants (e.g., c* in d{c*} length generalization) without explicit values or conditions. Full formal statements with explicit constants, dependencies on d, m, L, and |G|, and tight bounds are needed.
- Beyond NC1: While the paper claims optimization guarantees for NC1-complete tasks via CoT, whether similar guarantees extend (with richer architectures) to the broader P/poly expressivity known from prior work is an open theoretical direction.
- RL and SFT integration: The interplay between the proposed self-training and reinforcement learning or supervised fine-tuning on externally curated long CoT traces (as used in practice) is not analyzed; conditions under which these procedures help/hurt attention concentration and length generalization are unknown.
- Masking and self-attention choices: The causal mask allows the current answer token to attend to preceding tokens (including itself). The potential for degenerate self-attention behaviors, and whether alternative masking or decoder-only conventions alter the guarantees, is unexplored.
- Practical constraints on vocabulary scaling: The asymptotic regime d → ∞ underpins results; the behavior at realistic finite d (e.g., d ≈ 32k–128k), and how to translate asymptotic guarantees into practical guidance on model size and context length, is missing.
- Conditions for error-free state updates: Guarantees rely on exact compositional group actions without ambiguity. Real-world tasks often involve approximate updates, uncertainty, or partial observability; extensions to probabilistic state tracking or noisy actions are not provided.
Practical Applications
Immediate Applications
The following applications can be implemented with existing tooling and workflows, leveraging the paper’s training recipes, diagnostic insights, and synthetic tasks as proxies for real-world reasoning challenges.
- Training recipes to improve length generalization via CoT (software/AI engineering)
- Use case: Fine-tune or post-train existing LLMs with teacher-forcing CoT, first on short sequences (one- and two-step tasks) and then progressively longer sequences.
- Workflow: Adopt the two-stage curriculum (learn one-step state updates; then tune attention on two-step updates) to establish stable retrieval and token-to-token alignment, followed by standard scaling to longer tasks.
- Assumptions/dependencies: Availability of task instances with known semantics or ground truth; model supports autoregressive CoT; training regime approximates the paper’s setup (softmax attention, FFN).
- Category: Immediate Application.
- Attention concentration diagnostics to combat “context rot” (software/AI evaluation and reliability)
- Use case: Monitor attention heatmaps for concentration patterns (sharp diagonal bands between answer and predicate tokens) as a proxy for long-context retrieval robustness.
- Tools/products: Attention dashboards and unit tests that flag diluted attention in long contexts; regression tests that quantify concentration at increasing lengths.
- Assumptions/dependencies: Access to attention weights or proxies; ability to instrument inference/training; synthetic tasks (LEGO) or real tasks with similar state-tracking semantics.
- Category: Immediate Application.
- Synthetic curriculum generation using LEGO-style state-tracking tasks (academia, ML R&D)
- Use case: Build controlled datasets that encode state transitions with different algebraic structures (e.g., simply transitive actions versus symmetry actions) to probe and tune reasoning behavior.
- Tools/products: Dataset generators that create predicate/answer clause sequences with ground truth to measure length generalization and train attention concentration.
- Assumptions/dependencies: Synthetic tasks approximate key properties of real downstream reasoning tasks; downstream transfer may require domain adaptation.
- Category: Immediate Application.
- Length generalization test harness for production models (industry benchmarking, quality assurance)
- Use case: Establish acceptance tests that measure accuracy across training length and extrapolated lengths; include “constant-factor-only” generalization flags for symmetry-like tasks.
- Workflow: Evaluate models on short-length training data, then audit performance on longer sequences to detect extrapolation failures; integrate into CI for model releases.
- Assumptions/dependencies: Benchmarks reflect operational workloads; longer-context inference supported in deployment stack.
- Category: Immediate Application.
- Self-training pipeline to extend reasoning length in domains with distractors (software/AI training ops)
- Use case: For tasks that resemble symmetry actions (many-to-one mappings, multiple plausible predecessors), apply recursive self-training that “double-and-self-labels” CoT traces to bootstrap horizon length.
- Tools/products: Semi-automatic data generation pipelines that collect model-generated intermediate steps, verify them against trusted executors/rules, and use them for the next training stage.
- Assumptions/dependencies: Reliable verification filter or oracle to prevent error amplification; staged curriculum; sufficient compute to iterate several rounds.
- Category: Immediate Application.
- Resource-efficient on-device reasoning via CoT with shallow transformers (edge AI, robotics)
- Use case: Favor CoT with constant-depth models over deeper architectures in devices with tight compute/energy budgets to perform sequential state tracking (e.g., task progress monitoring, routine planning).
- Tools/products: Lightweight reasoning agents that externalize reasoning steps (intermediate state traces) and can be audited or partially executed.
- Assumptions/dependencies: Tasks exhibit state-tracking structure with stepwise updates; device supports long-context memory.
- Category: Immediate Application.
- Code assistant improvements on variable/state tracking (software engineering)
- Use case: Improve reliability in tracking variable values through multi-step transformations (refactorings, code execution snippets) by training with CoT and monitoring attention concentration.
- Workflow: Use LEGO-like curricula adapted to program semantics (assignments, function calls) to improve retrieval and reasoning depth.
- Assumptions/dependencies: Mapping from code semantics to structured state transitions; availability of ground-truth executors.
- Category: Immediate Application.
- Policy-oriented benchmarks for long-context reliability and extrapolation (policy, procurement, AI governance)
- Use case: Require models to demonstrate length-generalized performance on standardized state-tracking tests; report attention concentration metrics as a reliability indicator for long-context tasks.
- Tools/products: Public benchmark packs and compliance checklists that measure accuracy at and beyond training length, with distractor stress tests.
- Assumptions/dependencies: Benchmarks remain representative; vendors allow auditing beyond in-distribution lengths.
- Category: Immediate Application.
- Educational applications for step-by-step reasoning curricula (education/EdTech)
- Use case: Design graded exercise banks that explicitly encode step transitions and require learners (human or AI) to produce intermediate states; use recursive length expansion to build mastery.
- Tools/products: Tutors that reveal attention concentration as a learning signal and scaffold longer problems incrementally.
- Assumptions/dependencies: Educational tasks can be formalized as state transitions; evaluation can verify intermediate correctness.
- Category: Immediate Application.
Long-Term Applications
These applications build on the paper’s theoretical guarantees and mechanisms, but require further research, scaling, integration with more realistic tasks, or development of robust verification and safety tooling.
- General-purpose self-improving reasoning systems (software/AI platforms)
- Use case: Pipeline that continuously generates, verifies, and trains on longer CoT traces across heterogeneous domains, bootstrapping reasoning horizons autonomously.
- Potential products: “Reasoning growth engines” that combine self-training with verification (symbolic executors, simulators, or trusted APIs), scaling length to the practical maximum.
- Dependencies: Strong verification oracles; safeguards against compounding errors; orchestration over diverse task distributions; compute and memory scaling.
- Category: Long-Term Application.
- Robust long-context assistants for complex workflows (healthcare, finance, legal, operations)
- Use case: Track patient states across lengthy timelines, portfolio/risk state over extended periods, or case state across lengthy legal docs—using CoT and attention concentration to mitigate distractors.
- Potential tools: Domain-specific state-tracking schemas (ontologies) and validators, long-context memory managers, attention concentration regularizers.
- Dependencies: Precise domain modeling (actions, states, constraints); privacy/security; long-context inference capacity; validated ground truth.
- Category: Long-Term Application.
- Formal reliability metrics and governance around attention concentration (policy, safety, standards)
- Use case: Standardize reporting on retrieval robustness, including measures of concentration versus dilution under long contexts and distractors; use as part of model safety evaluations.
- Potential tools: Regulatory test suites; third-party audits with attention access or certified proxies; disclosure protocols for length extrapolation.
- Dependencies: Agreement on metrics; cooperation from vendors; handling proprietary architectures and positional encodings beyond NoPE.
- Category: Long-Term Application.
- Architectures and training methods that generalize beyond LEGO to real-world sequential tasks (academia, applied ML)
- Use case: Extend theory and practice from synthetic group actions to realistic, noisy, partially observed state machines (e.g., multi-agent systems, complex software stacks).
- Potential workflows: Hybrid neuro-symbolic verification of intermediate steps; curriculum design based on domain-specific algebraic structures; position encoding choices that preserve length generalization.
- Dependencies: Task reformulations that expose action/state semantics; improved positional encoding schemes; empirical validation across domains; sample-efficient training.
- Category: Long-Term Application.
- Compiler-like CoT planners with verified intermediate states (software tooling, DevOps)
- Use case: CoT “compilers” that turn high-level goals into verified sequences of state updates (deploy plan, rollback/recovery steps) with attention-aware retrieval and self-training to extend operational horizons.
- Potential products: Planning-as-code tools; CoT interpreters that emit verifiable traces usable by automation systems.
- Dependencies: Strong executors/validators; integration into CI/CD and operational stacks; trace storage and retrieval.
- Category: Long-Term Application.
- Edge robotics with sequential planning and state tracking (robotics, IoT)
- Use case: Small transformers with CoT handle extended task sequences (assembly, inspection, navigation) on-device, leveraging attention concentration to focus on relevant history and self-training to expand horizons.
- Potential tools: Lightweight planners; trace-based verification; fallback to symbolic checks when attention concentration degrades.
- Dependencies: Real-time constraints; long-context memory; safety certifications; robust sensor-to-state mapping.
- Category: Long-Term Application.
- Long-context retrieval and RAG systems guided by attention concentration (software/AI infra)
- Use case: Design retrieval augmentation to foster concentration on relevant windows and discourage distractors, using CoT to structure queries and state updates.
- Potential products: Attention-aware retrievers and memory managers; “concentration regularizers” during fine-tuning.
- Dependencies: Access to attention internals or reliable proxies; dataset curation; integration with vector databases and long-context models.
- Category: Long-Term Application.
- Complexity-aware training strategies for resource-limited environments (energy/compute efficiency)
- Use case: Replace deeper networks with shallow models plus CoT where tasks are inherently sequential but verifiable, aligning with the paper’s optimization guarantee beyond TC0 via CoT.
- Potential tools: Profilers that trade depth for CoT length; energy-aware schedulers; mobile/embedded AI SDKs.
- Dependencies: Verification of intermediate steps; task selection that matches state-tracking structures; performance audits under real constraints.
- Category: Long-Term Application.
Cross-cutting assumptions and dependencies
- Synthetic-to-real transfer: The paper’s results are derived from LEGO state-tracking tasks with well-defined group actions; real tasks must be reformulated to expose comparable action/state semantics and verification.
- Architecture dependence: Results assume a one-layer transformer with softmax attention, NoPE, block-sparse attention parameters, smooth ReLU, and teacher forcing; deviations (e.g., different positional encodings, multi-layer stacks) may change generalization behavior.
- Verification and error control for self-training: Recursive self-training requires reliable filtering to prevent error amplification; domain-specific oracles/simulators are critical.
- Long-context capacity: Hardware and model memory must support longer contexts as reasoning horizons expand; inference-time policies (e.g., caching, chunking) should preserve attention concentration.
- Distractor prevalence: Tasks resembling symmetry actions (many-to-one mappings, multiple plausible predecessors) will need more aggressive curricula or verification to achieve robust length generalization.
Glossary
- attention concentration: The phenomenon where a transformer's attention focuses sharply on task-relevant tokens, enabling step-wise retrieval in long contexts. "Our theory uncovers the mechanism of attention concentration that explains the varying degrees of length generalization."
- autoregressive transformer: A model that generates outputs token-by-token, conditioning each prediction on previously generated tokens. "In this work, we focus on an autoregressive transformer whose block consists of a softmax attention layer followed by a position-wise feed-forward network, as described below."
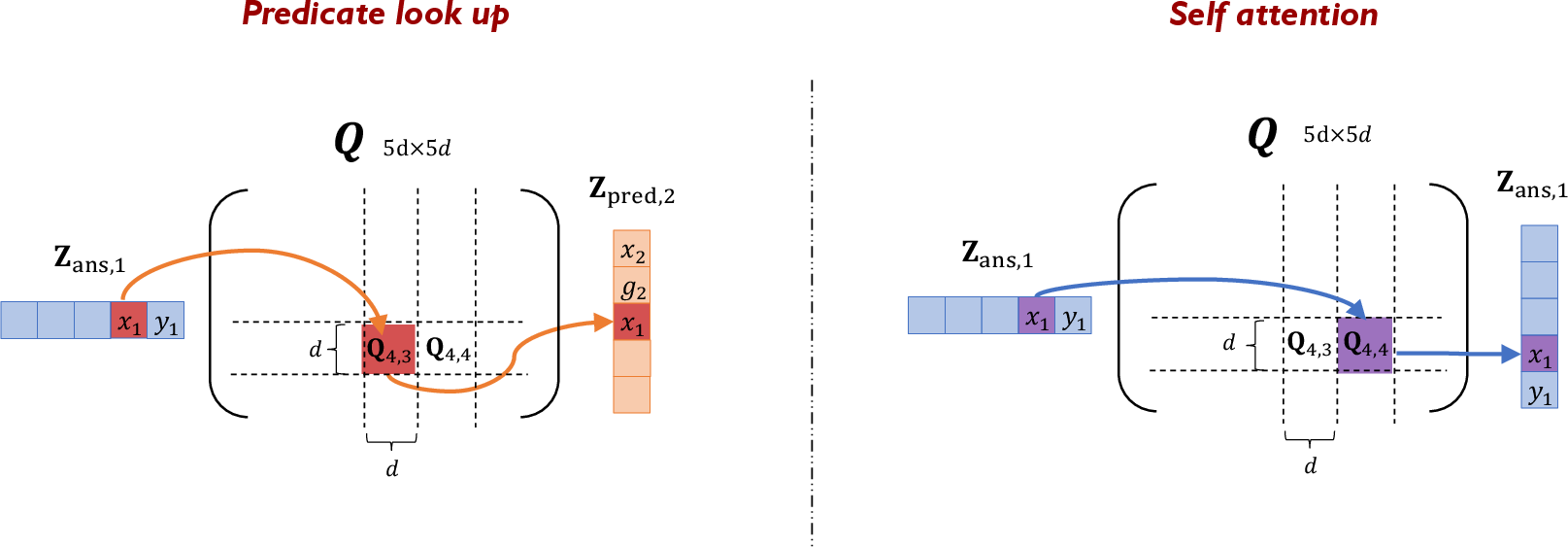
- block-sparsity pattern: A structural constraint that restricts which submatrices of the attention parameter are trainable, simplifying analysis of attention dynamics. "Moreover, to simplify the analysis of attention dynamics, we impose a fixed block-sparsity pattern on the attention parameter $\Qb$."
- Boolean circuit: An acyclic network of logic gates computing a Boolean function, used to characterize computational complexity. "A Boolean circuit is a finite acyclic network of logic gates that computes a Boolean function on for some fixed ."
- causal mask: A masking mechanism ensuring a token attends only to previous (or itself) tokens in autoregressive decoding. "Since the model is autoregressive, a standard causal mask is applied to ensure that the latest (answer) token attends only to preceding tokens (including itself)."
- chain-of-thought (CoT) reasoning: A technique where models generate intermediate steps before the final answer to solve complex tasks. "Transformer-based LLMs achieve state-of-the-art results on complex reasoning tasks via chain-of-thought (CoT) reasoning..."
- circuit complexity: A framework evaluating computation by circuit size, depth, and gate types to classify problem difficulty. "Historically, circuit complexity has been used extensively to study the power of neural networks..."
- constant-depth transformers: Transformers whose computation depth does not scale with input size, limiting expressiveness without CoT. "seminal work~... showed that constant-depth transformers without CoT behave as shallow circuits and are restricted to express the circuit complexity class ."
- context rot: Degradation of model performance as context length increases. "context rot: namely, a phenomenon in which model performance degrades as the number of tokens in the context increases"
- cyclic group (C6): A group where elements form a cycle under the group operation; used as a simply transitive action example. "Length generalization results of cyclic () vs. \ symmetry () tasks."
- feed-forward network (FFN): A position-wise neural sublayer in transformers applied after attention. "a one-layer transformer block with softmax attention and a feed-forward network (FFN), trained by GD with no positional encoding (NoPE)."
- gradient descent (GD): An optimization method updating parameters in the direction of the loss gradient. "trained via gradient descent (GD)"
- group action: A rule describing how group elements transform states in a space. "Given a group acting on a state space , the goal is to compute the final state ..."
- LEGO (Learning Equality and Group Operations): A synthetic language/task for studying state-tracking and reasoning in transformers. "We focus on a specific formulation of the state-tracking problem, LEGO (Learning Equality and Group Operations)"
- length generalization: The ability of a model trained on shorter sequences to extrapolate effective reasoning to longer sequences. "Another key question... is whether large models can extrapolate their reasoning beyond the sequence lengths of the training data: a feature known as length generalization."
- long-context reasoning: Reasoning that requires retrieving and processing information over extended token sequences. "linking the retrieval robustness of the attention layer to the state-tracking task structure of long-context reasoning."
- non-solvable group: A group whose derived series does not terminate at the identity; central to NC1-complete word problems. "The word problem of every finite non-solvable group is -complete."
- NoPE (no positional encoding): A transformer configuration that omits positional embeddings in attention. "trained by GD with no positional encoding (NoPE)."
- positional encoding: Representations injected into transformer inputs to encode token positions. "Architectural choices, including positional encoding and attention variants, can influence generalization considerably"
- recursive self-training: A curriculum where a model is retrained on its own generated traces to extend capabilities. "we introduce a self-training curriculum that recursively trains the model on its own CoT traces"
- self-improvement: The process by which a model enhances its abilities through iterative self-training. "A one-layer transformer, trained with a recursive self-training scheme, can self-improve"
- simply transitive action: A group action that is both free and transitive, giving a unique mapping between any two states. "A simply transitive action is free and transitive; that is, there is {\em a unique} group element $g \in \cG$ mapping any state to another."
- smooth ReLU (sReLU): A differentiable approximation to ReLU used to facilitate analysis and optimization. "sReLU(x)"
- softmax attention: An attention mechanism where weights are computed via a softmax over similarity scores. "a one-layer transformer block with softmax attention and a feed-forward network (FFN)"
- stabilizer: The subgroup of elements that fix a given state under a group action. "these two types of actions have different sizes of stabilizers, even when the group $\cG$ is the same."
- state-tracking: Computing the resulting state after applying a sequence of transformations from an initial state. "we present a theoretical analysis of transformers learning on synthetic state-tracking tasks with gradient descent."
- symmetry group: The group of permutations on n elements, denoted , used as a canonical non-solvable example. "for the canonical action of the symmetry group on "
- teacher forcing: A training strategy providing ground-truth intermediate steps to guide next-token prediction. "This is a teacher forcing style CoT objective"
- threshold gates: Circuit gates that output based on whether weighted inputs exceed a threshold (e.g., MAJORITY). "unbounded fan-in gates augmented with threshold (e.g., ) gates."
- word problem: Deciding whether a product of group elements equals the identity. "The word problem of every finite non-solvable group is -complete."
Collections
Sign up for free to add this paper to one or more collections.