Papers
Topics
Authors
Recent
Assistant
AI Research Assistant
Well-researched responses based on relevant abstracts and paper content.
Custom Instructions Pro
Preferences or requirements that you'd like Emergent Mind to consider when generating responses.
Gemini 2.5 Flash
Gemini 2.5 Flash 148 tok/s
Gemini 2.5 Pro 48 tok/s Pro
GPT-5 Medium 34 tok/s Pro
GPT-5 High 40 tok/s Pro
GPT-4o 101 tok/s Pro
Kimi K2 183 tok/s Pro
GPT OSS 120B 443 tok/s Pro
Claude Sonnet 4.5 35 tok/s Pro
2000 character limit reached

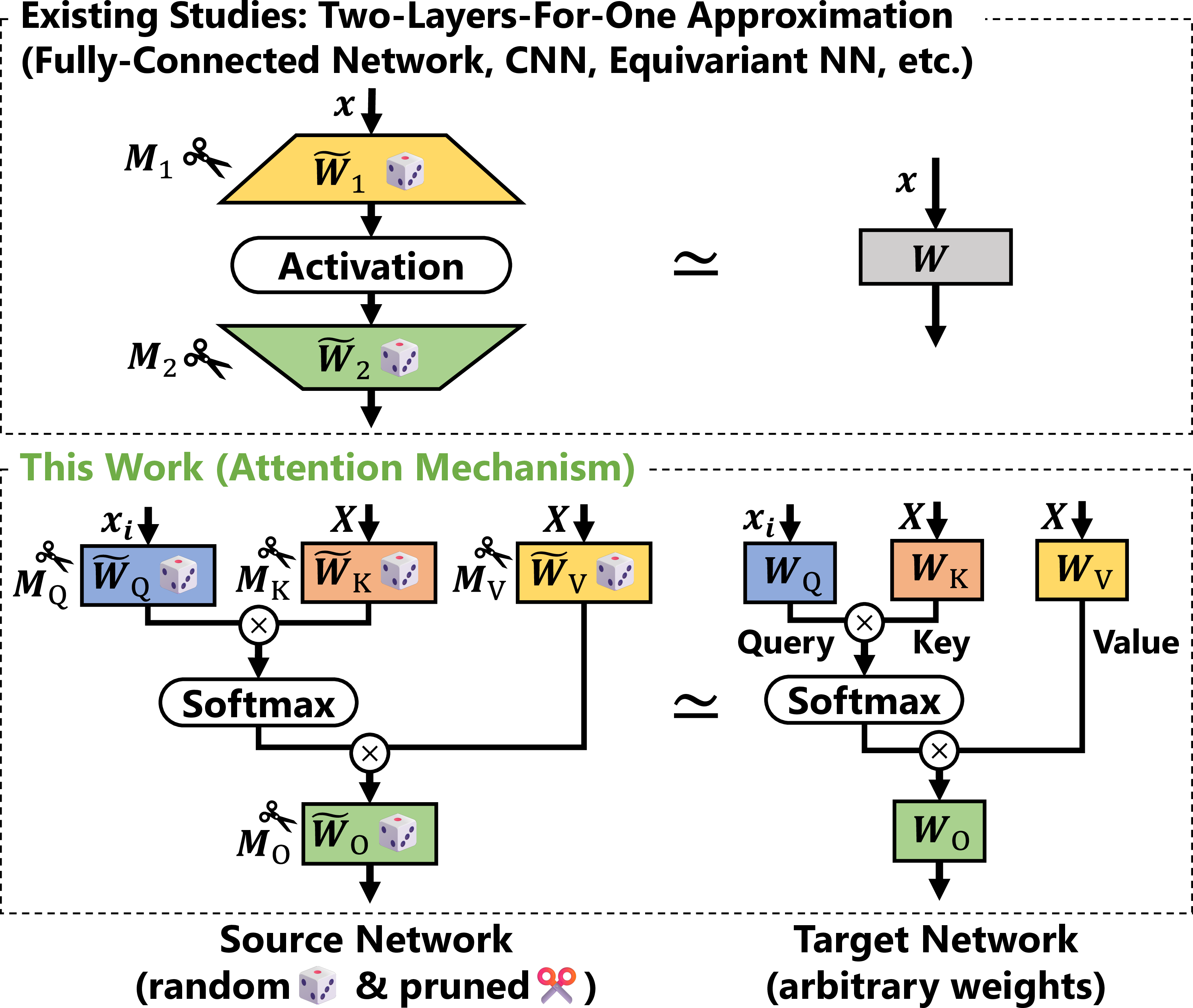
The Strong Lottery Ticket Hypothesis for Multi-Head Attention Mechanisms (2511.04217v1)

Published 6 Nov 2025 in cs.LG and cs.AI

Abstract: The strong lottery ticket hypothesis (SLTH) conjectures that high-performing subnetworks, called strong lottery tickets (SLTs), are hidden in randomly initialized neural networks. Although recent theoretical studies have established the SLTH across various neural architectures, the SLTH for transformer architectures still lacks theoretical understanding. In particular, the current theory of the SLTH does not yet account for the multi-head attention (MHA) mechanism, a core component of transformers. To address this gap, we introduce a theoretical analysis of the existence of SLTs within MHAs. We prove that, if a randomly initialized MHA of $H$ heads and input dimension $d$ has the hidden dimension $O(d\log(Hd{3/2}))$ for the key and value, it contains an SLT that approximates an arbitrary MHA with the same input dimension with high probability. Furthermore, by leveraging this theory for MHAs, we extend the SLTH to transformers without normalization layers. We empirically validate our theoretical findings, demonstrating that the approximation error between the SLT within a source model (MHA and transformer) and an approximate target counterpart decreases exponentially by increasing the hidden dimension of the source model.

Summary

  • The paper proves that strongly pruned, randomly-initialized MHA networks contain subnetworks (SLTs) that approximate the performance of arbitrary MHA setups.
  • It demonstrates that SLTs extend to full transformer architectures without normalization layers, with error reduction linked to hidden dimension scaling.
  • Empirical results confirm exponential error decay, sequence length independence, and effective query-key scaling for improved weight initialization.

The Strong Lottery Ticket Hypothesis for Multi-Head Attention Mechanisms

Introduction

The paper explores the longstanding "Strong Lottery Ticket Hypothesis" (SLTH) by extending its application to Multi-Head Attention (MHA) mechanisms, which are critical components of transformer architectures. The hypothesis posits that within overparameterized neural networks exist subnetworks (strong lottery tickets, or SLTs) that can equate the performance of fully-trained models without requiring training. Recent studies have successfully demonstrated SLTH in various neural architectures, yet its application to transformer-based models, specifically MHAs, remained unexplored. This gap is addressed by theoretically proving the existence of SLTs in randomly initialized MHA networks, thereby extending the SLTH's relevance to transformer architectures sans normalization layers.

Theoretical Contribution

MHA and The Strong Lottery Ticket Hypothesis

The primary theoretical contribution is the proof of SLTs within MHA mechanisms. The authors establish that a suitably pruned, randomly-initialized MHA with input dimension dd and HH heads contains an SLT approximating any arbitrary MHA with the same input dimension, provided the hidden dimension is O(dlog⁡(Hd3/2))O(d\log(Hd^{3/2})). This result is significant as it demonstrates that MHA mechanisms inherit the SLTH's robust performance guarantees through a novel proof technique that parallels yet diverges from conventional SLTH proofs. Figure 1

Figure 1: Comparison of the approximation techniques in conventional theories of the SLTH (top) and in our attention-specific approach (bottom). This work demonstrates that an arbitrary attention mechanism can be approximated by pruning a randomly initialized one.

The proof hinges on approximating the inner product operations within MHA (query-key and value-output interactions) as neural networks with different layer configurations. By merging projection matrices and utilizing a variant of the two-layers-for-one approximation, it was demonstrated that SLTs do indeed exist in MHA setups, bypassing the need for additional intermediary network layers as seen in previous fully-connected network studies.

Extension to Transformer Architectures

Building on the SLT presence in MHAs, the paper extends its scope to full transformer architectures devoid of normalization layers. The authors prove that these transformers can be initialized randomly and contain SLTs matching the performance of arbitrary transformers with similar structures. This finding broadens the SLTH's applicability and offers a foundational understanding of the inherent capabilities in modern transformer-driven models.

Empirical Validation

Empirical results affirm the theoretical predictions. Key observations include:

  • Approximation Error: The error between source and target MHA decreases exponentially with increased hidden dimensions, aligning with the theorized O(log⁡(1/ϵ))O(\log(1/\epsilon)) requirement described in the main theorem. Figure 2

    Figure 2: The approximation error epsilon of SLTs within a source MHA for the hidden dimensions.

  • Sequence Length Independence: Experiments confirm that the approximation quality remains consistent irrespective of sequence length, supporting the theoretical claim regarding dimension-independence from input length TT. Figure 3

    Figure 3: The approximation error epsilon of SLTs within an MHA for the sequence length T.

  • Transformer Block Observations: The consistency of error reduction across different numbers of blocks was demonstrated, where the approximation error decreases rapidly for all block numbers, attesting to the theory's robustness. Figure 4

    Figure 4: The approximation error epsilon of SLTs within a randomly initialized transformer for the source hidden dimensions.

Practical Implications

The theoretical insights extend to practical applications, particularly weight initialization strategies. It was observed that scaling the query and key weights substantially enhances SLT performance in GPT-2 models. Theoretical assumptions provided a nearly optimal scaling factor for query and key weights, resulting in lowered loss and enhanced model efficiency. Figure 5

Figure 5: Loss comparison between SLTs with and without query and key weight scaling. By introducing a scale based on our theoretical assumptions, we can obtain better SLTs.

Conclusion

The paper provides a rigorously grounded framework connecting the SLTH to MHA and transformer models, highlighting their intrinsic capability to house performant subnetworks without training. This bridging of theory and practice not only advances SLTH research but also optimizes weight initialization strategies directing transformational model training to be more efficient. These insights introduce new research directions focusing on the inherent efficacy of overparameterized transformer models, potentially influencing future AI advancements.

File Document Download Save Streamline Icon: https://streamlinehq.com PDF File Document Download Save Streamline Icon: https://streamlinehq.com Markdown
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Explain it Like I'm 14

The Strong Lottery Ticket Hypothesis for Multi-Head Attention Mechanisms — Explained Simply

What is this paper about?

This paper studies a big idea in machine learning called the Strong Lottery Ticket Hypothesis (SLTH). It says that inside a large, randomly built neural network, there exist small subnetworks (called strong lottery tickets, or SLTs) that can perform very well without any training. The paper focuses on proving this idea for transformers, the powerful models behind tools like ChatGPT and BERT. In particular, it looks at the core part of transformers: the multi-head attention (MHA) mechanism.

What questions are the researchers asking?

The paper asks:

  • Do multi-head attention mechanisms (MHA) in transformers contain strong lottery tickets (SLTs)?
  • If they do, how “big” does the attention mechanism need to be for these SLTs to exist?
  • Can this idea be extended to full transformer models (without normalization layers)?
  • What happens to the quality of these SLTs as we change how wide the attention layers are or how long the input sequence is?

How did they approach the problem?

To make this understandable, think of a transformer’s attention mechanism like a group of “heads” (team members) that each look at the input and decide what parts are important. Each head uses three sets of weights:

  • Query: “What am I looking for?”
  • Key: “What do I have?”
  • Value: “What information do I pass along?”

The attention score is computed by comparing queries with keys (like matching questions to relevant facts), and then using values to produce the output. A softmax function makes sure the attention scores add up nicely.

Here’s the key trick the researchers used:

  • Instead of trying to match the query and key weights separately (which is hard), they combine them into one “merged” matrix. Think of it like combining two steps of a recipe into one step that gives the same result.
  • The same merging idea is applied to the value and output weights.
  • They then use a known mathematical technique (the “two-layers-for-one” approximation) to show that by pruning (turning off) the right connections in a random, wider network, you can closely imitate any target attention mechanism.
  • They also analyze the softmax part carefully to show that the error does not blow up when the input sequence gets longer.

In simpler terms: they prove that if you start with a big enough random attention mechanism and turn off most of its connections in the right way, the remaining small piece can act like any attention mechanism you want—without training.

What did they find, and why is it important?

Here are the main findings:

  • Multi-head attention contains strong lottery tickets. If the attention’s hidden dimensions (the number of “channels” or width inside query/key/value) are large enough—only by a logarithmic amount relative to model size—then pruning can reveal an SLT that closely imitates any target attention mechanism.
  • The required width grows roughly like “input dimension times a logarithm” of other model size terms. In simple terms, you don’t need the source model to be extremely huge—just a bit wider than the target in a smart way.
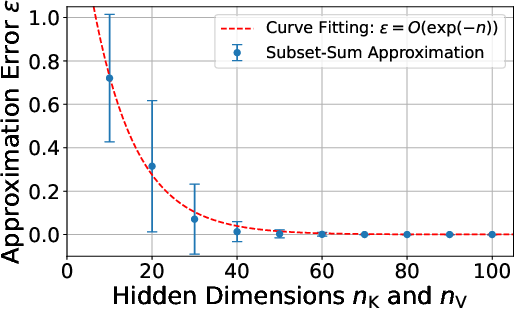
  • The quality of approximation improves exponentially as you increase the hidden dimensions. So making the attention slightly wider can make SLTs much more accurate very quickly.
  • The approximation error does not increase with longer input sequences. This matters for transformers, which often process long texts.
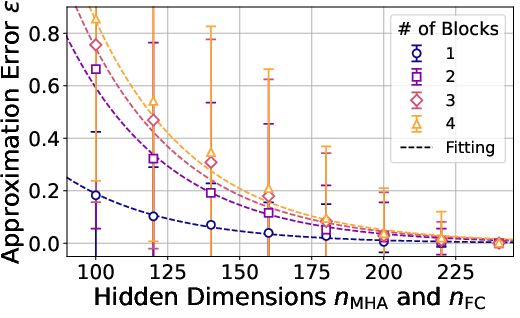
  • They extend the result to full transformers (without normalization layers). That means entire transformer blocks (attention + feed-forward) also contain SLTs that can imitate target transformers, if they are a bit wider and properly pruned.
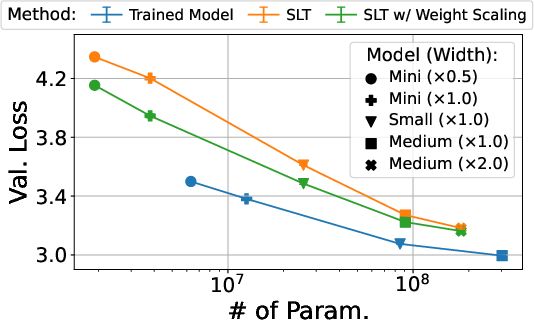
  • A practical tip: scaling the query and key weights at initialization (by a specific factor) helps find better SLTs in real models. In experiments with GPT-2 variants on a language dataset, this improved performance compared to not scaling.

How did they test their ideas?

  • Synthetic tests: They built simple attention and transformer models and tried to approximate a “target” model by pruning a random “source” model. They measured how the error changed as they increased the hidden dimensions and the input length. Results showed:
    • Error drops exponentially as the attention becomes wider.
    • Error stays bounded even as the sequence gets longer.
  • Real models: Using GPT-2-type transformers trained with a pruning-based method (instead of training weights), they found that scaling the query and key weights as suggested by their theory led to better subnetworks (lower loss), consistently across different model sizes.

Why does this matter?

  • Understanding transformers: This work gives a solid mathematical foundation for why transformers can contain powerful subnetworks even before training. That helps us understand why making models bigger often helps, and why pruning can be so effective.
  • Practical benefits: If good subnetworks already exist at initialization, we can aim to find them more efficiently (for speed, memory savings, or robustness) instead of training all weights.
  • Better initialization strategies: The paper’s suggested weight scaling for attention helped in real models, hinting that theory can guide practical choices to improve performance.

What could this lead to?

  • Smaller, faster models: If we can reliably find strong lottery tickets inside large transformers, we can deploy compact models that work well without full training.
  • New pruning and initialization methods: Their techniques may inspire better ways to set up and shrink transformers from the start.
  • Deeper understanding of overparameterization: It adds evidence that “overly large” models are not wasteful—they hide many capable subnetworks we can uncover.

In short, the paper shows that the magic of strong lottery tickets also exists inside the attention parts of transformers, and gives both theory and experiments to back it up.

Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Knowledge Gaps

Knowledge Gaps, Limitations, and Open Questions

Below is a single, consolidated list of unresolved issues that future work could address to strengthen, generalize, and operationalize the paper’s results.

  • Theory excludes normalization layers (LayerNorm/RMSNorm); provide SLTH proofs and width bounds for transformers with normalization, which are standard in practice.
  • FFNs are modeled as single-layer (or two-layer ReLU) projections; extend proofs to realistic FFNs (GELU, biases, multi-layer depth) with explicit width/error constants.
  • Bias terms are absent in all linear projections; analyze how biases affect merged-matrix approximations and resulting width requirements.
  • Results are stated “given inputs of length T” and bound errors over the fixed sequence X; develop input-distribution-level or uniform-in-input guarantees (data-independent SLTs).
  • Initialization assumes uniform distributions and query/key scaling by n_K1/4; generalize to common initializations (Xavier/He, Gaussian) and derive necessary/sufficient scaling factors.
  • The n_K1/4 scaling is motivated analytically and supported empirically; determine theoretically optimal scaling as a function of (d, H, n_K) and whether alternatives yield tighter bounds.
  • Softmax error bound (Lemma 3) requires α-bounded inputs; characterize when α remains T-independent in real pipelines (e.g., with positional encoding, normalization), or propose strategies to enforce it.
  • Tightness of width bounds: establish lower bounds for MHAs to test whether O(d log(…)) overparameterization is optimal or can be improved.
  • Union bound across heads scales pessimistically with H; develop joint-head analyses that avoid linear-in-H failure probability and reduce hidden-dimension requirements.
  • Cross-attention (query from one sequence, keys/values from another) is not covered; extend QK/VO merging and softmax analyses to encoder-decoder attention.
  • Positional encodings (sinusoidal/learned/rotary) are omitted; analyze their interaction with the merged-matrix approximation and the softmax error propagation.
  • Attention variants (entmax/sparsemax, temperature schedules, gating) are excluded; derive analogs of Lemma 3 and end-to-end SLTH guarantees for these mechanisms.
  • Practical mask selection relies on subset-sum-style pruning; provide scalable, polynomial-time algorithms with approximation guarantees for large models, or tighter complexity analyses.
  • The merged-matrix approximation lemma gives max-norm guarantees with unspecified universal constant C; supply explicit constants to make width budgets actionable.
  • Error accumulation across B blocks is summarized via opaque quadratic forms f_i, g_i with constants c_1, c_2; present closed-form expressions and practical recipes for block-wise width allocation.
  • Heads are treated independently and concatenated via W_O; investigate inter-head dependencies (e.g., shared parameterizations, head mixing) and their impact on SLTs.
  • Empirical validation focuses on single-head synthetic setups and limited GPT-2 edge-popup experiments; test multi-head cases, larger H, realistic tasks (LM, translation), and broader architectures.
  • Edge-popup training finds masks via backprop but does not quantify computational cost or scalability; benchmark mask-finding efficiency vs. performance and propose budget-aware methods.
  • Robustness to input perturbations, distribution shift, and noise is not analyzed; develop stability guarantees for SLTs and measure empirical robustness.
  • Dropout, stochastic depth, and training-time regularizers are excluded; analyze their compatibility with SLTH guarantees and effect on approximation error.
  • Sequence-length independence is shown under α-bounded inputs; examine regimes where ||X|| can grow with T and propose normalization or scaling to maintain T-independent bounds.
  • The theoretical framework assumes arbitrary attention masks but not dynamic or learned masking (e.g., routing); extend guarantees to data-dependent masks.
  • Generalize to emerging attention designs (multi-query/grouped-query, KV cache reuse, rotary embeddings) with corresponding SLTH proofs.
  • Provide constructive procedures to compute masks for a given target model (beyond random trials over 100 sources), with complexity/performance guarantees.
  • Quantify success probabilities precisely (beyond “with high probability”), including tail behavior and finite-size effects, to guide practical deployment.
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Practical Applications

Immediate Applications

Below are practical applications that can be deployed now or piloted with existing tooling, drawing on the paper’s theoretical guarantees, empirical findings, and the proposed initialization strategy.

  • SLT-aware initialization for transformers in production
    • Sector: software, AI/ML infrastructure
    • Application: Introduce a lightweight initializer that scales query/key weights by approximately n_K1/4 at model startup to improve the quality of subnetworks discovered by pruning at initialization.
    • Tools/Products/Workflows: Framework plugins (e.g., PyTorch/TensorFlow initializer wrappers), HuggingFace Transformers integration, config flag “qk_scale=n_K1/4”.
    • Assumptions/Dependencies: Benefits observed with edge-popup mask optimization; best for attention blocks and may require tuning for models with LayerNorm or different initializations.
  • Mask-only optimization to find strong tickets at initialization
    • Sector: software, healthcare, finance, robotics (on-device AI), education
    • Application: Use pruning-mask training (e.g., edge-popup) instead of weight updates to find performant subnetworks in large attention-heavy models, reducing compute and memory for inference or task-specific adaptation.
    • Tools/Products/Workflows: “SLT Finder” pipelines that optimize binary masks per attention head; CI/CD steps that generate sparse inference-ready models without full training.
    • Assumptions/Dependencies: Works best with random initialization and Q/K scaling; performance depends on mask optimization algorithm quality and task complexity.
  • Width planning for attention blocks with guaranteed approximation error
    • Sector: software (MLOps/AutoML), energy (Green AI)
    • Application: Use the closed-form scaling n_K, n_V = O(d log(H d3/2/ε)) to provision hidden dimensions for target error ε and number of heads H, ensuring SLT existence with high probability.
    • Tools/Products/Workflows: “MHA Width Planner” that computes minimum width per module given desired approximation error; integrated into AutoML model sizing and cost/latency planning.
    • Assumptions/Dependencies: Guarantees most directly apply to transformers without normalization layers and random weight distributions similar to U[−1,1]; constants may be conservative.
  • Long-context deployment planning that does not blow up with sequence length T
    • Sector: software (LLM platform teams), robotics (perception with long contexts), finance (long compliance documents)
    • Application: Use the T-independent error bound in softmax analysis to confidently deploy SLT-based attention for long-context tasks without exponential error growth.
    • Tools/Products/Workflows: Capacity planning and SLT validation suites that test error vs. T; “long-context safety” checks that rely on the bound from the paper.
    • Assumptions/Dependencies: Requires bounded input norms and accurate mask-based approximations of Q/K projections.
  • Compressed, energy-efficient attention for edge devices
    • Sector: robotics, healthcare (clinical NLP on-device), consumer mobile (offline assistants), IoT
    • Application: Ship sparse SLTs discovered at initialization to run attention-heavy workloads locally, saving battery, reducing latency, and enabling offline functionality.
    • Tools/Products/Workflows: Edge inference runtimes supporting masked attention weights; deployment scripts that export sparse subnetworks from random initializations.
    • Assumptions/Dependencies: Mask identification needs a lightweight optimizer; performance depends on available width and on-device memory.
  • SLT-aware distillation-lite workflows for attention modules
    • Sector: software (model compression), education (student devices), finance (on-prem deployment)
    • Application: Approximate a trained attention module with a pruned randomly initialized counterpart by optimizing masks, lowering storage and inference cost without full retraining.
    • Tools/Products/Workflows: “Attention SLT Approximation” toolkit that takes target Q/K/V/O and a random source block and returns masks guaranteeing small approximation error.
    • Assumptions/Dependencies: Theoretical guarantees are strongest for transformers without normalization layers; practical distillation needs compatible initialization and sufficient width.
  • Rapid prototyping of attention models with training-free baselines
    • Sector: academia, software
    • Application: Use SLTs to create baseline models quickly from random initializations, enabling ablation studies, teaching, and benchmarking with minimal compute.
    • Tools/Products/Workflows: Synthetic experiment harness replicating exponential error decay vs. width; notebooks demonstrating SLT formation in MHA/transformers.
    • Assumptions/Dependencies: Best fit to synthetic or controlled tasks; performance on complex tasks may require additional fine-tuning of masks.
  • AutoML integration for “sparsity-first” design
    • Sector: software (AutoML), energy
    • Application: Incorporate SLT existence bounds into automated model sizing and pruning strategies, prioritizing sparse attention configurations that meet error targets.
    • Tools/Products/Workflows: AutoML constraints “target ε per block” and “maximize sparsity”; policy-based optimizers selecting width via the paper’s formulas.
    • Assumptions/Dependencies: Accuracy bounds depend on initialization and absence of normalization layers; generalization to modern architectures may need empirical calibration.
  • Curriculum and benchmarking for SLT research
    • Sector: academia, education
    • Application: Standardize evaluation of SLT behavior in attention via synthetic tasks; include Q/K scaling and mask-only optimization in teaching materials and reproducible benchmarks.
    • Tools/Products/Workflows: Public repos with subset-sum-inspired mask optimization; datasets for long T and varying width; shared baselines.
    • Assumptions/Dependencies: Educational scope; results are most robust under paper’s technical conditions.
  • Green AI reporting with SLT-aware compression
    • Sector: policy (corporate sustainability), energy
    • Application: Report energy savings achieved by SLT-first model deployment pipelines that minimize training and inference compute via sparse subnetworks.
    • Tools/Products/Workflows: Sustainability dashboards linking sparsity level and expected carbon reduction; SLT KPI tracking.
    • Assumptions/Dependencies: Requires organizational buy-in and measurement of compute; impact size depends on mask optimization efficacy and inference workload.

Long-Term Applications

The following applications require further research, scaling, or engineering development, especially to generalize beyond the paper’s assumptions (e.g., normalization layers) or to industrialize mask search and hardware support.

  • Near training-free transformer assembly via mask compilation
    • Sector: software, AI platform providers
    • Application: Compile masks that approximate trained attention blocks on randomly initialized networks, reducing or eliminating weight training for new tasks or domains.
    • Tools/Products/Workflows: “SLT Compiler for Attention” that ingests a target model and emits mask-only approximations; potential integration with MILP solvers (e.g., Gurobi) or advanced heuristics.
    • Assumptions/Dependencies: Subset-sum style mask search is computationally hard at scale; success depends on width, initialization, and potential extensions to LayerNorm.
  • SLT-aware accelerators and hardware co-design
    • Sector: hardware, robotics, edge computing
    • Application: Design chips that execute masked attention efficiently (e.g., dynamic gating of Q/K/V/O paths, compressed storage formats, mask-aware memory layouts).
    • Tools/Products/Workflows: Hardware support for binary masks, fast subset-sum/heuristic mask solvers on-device, compilers that schedule sparse attention.
    • Assumptions/Dependencies: Requires stable mask formats, standard sparsity patterns, and tight co-design between software and silicon.
  • Standardization of SLT-first initialization and pruning protocols
    • Sector: software standards, policy
    • Application: Establish industry norms for attention initialization (Q/K scaling), mask optimization procedures, and reporting of approximation error guarantees.
    • Tools/Products/Workflows: Specifications, library defaults, conformance tests; policy guidance on energy-efficient model building.
    • Assumptions/Dependencies: Community consensus; empirical validation across models with normalization and modern training tricks.
  • Long-context LLMs with provable error control via SLTs
    • Sector: software (LLMs), finance, healthcare, legal
    • Application: Build long-context systems whose attention approximation error does not grow with sequence length T, enabling reliable processing of very long documents or logs.
    • Tools/Products/Workflows: SLT-based attention in long-context architectures; auditing tools certifying T-independent error bounds.
    • Assumptions/Dependencies: Extending theory to normalized transformers and practical datasets; robust mask search at scale.
  • Privacy-preserving on-device personalization by mask updates
    • Sector: consumer, healthcare, finance
    • Application: Personalize models by updating masks (not weights), keeping sensitive data on-device and reducing gradient leakage risks.
    • Tools/Products/Workflows: “Mask Personalization” APIs that learn sparse gates from private data; federated protocols exchanging masks rather than weights.
    • Assumptions/Dependencies: Requires evidence that mask optimization limits privacy risks; needs on-device compute for mask search.
  • SLT-informed distillation services for enterprise models
    • Sector: software, energy
    • Application: Offer services that take trained models and return sparse, mask-approximated attention modules for carbon-aware inference and cost reduction.
    • Tools/Products/Workflows: Cloud pipelines that perform SLT mask search, validate approximation error, and deploy compressed models to edge or on-prem.
    • Assumptions/Dependencies: Industrial-grade mask solvers; interoperability with diverse architectures (LayerNorm, residuals, multi-block interactions).
  • Robustness and safety via random-initial SLTs
    • Sector: safety-critical systems (autonomous robotics, healthcare)
    • Application: Investigate whether SLT-based attention from random initializations yields complementary robustness properties (e.g., reduced overfitting) under distribution shift.
    • Tools/Products/Workflows: Stress-testing suites comparing SLT vs. trained weights; certification workflows if robustness benefits materialize.
    • Assumptions/Dependencies: Requires empirical validation; not guaranteed by current theory.
  • Extending theory to normalized transformers and modern training regimes
    • Sector: academia
    • Application: Generalize SLT guarantees beyond transformers without normalization layers; incorporate LayerNorm, residual scaling, learned positional encodings.
    • Tools/Products/Workflows: New proofs, improved constants, broader initialization recipes; open-source reference implementations.
    • Assumptions/Dependencies: Nontrivial mathematical challenges; likely needs refined approximation lemmas and error propagation analyses.
  • Synergy with quantization and structured sparsity
    • Sector: software, hardware
    • Application: Combine SLT masks with quantization or block-sparse patterns to amplify compression and speed gains while maintaining accuracy.
    • Tools/Products/Workflows: Joint compression toolchains that co-optimize masks and quantization levels; mask-aware kernel libraries.
    • Assumptions/Dependencies: Requires careful calibration; error bounds need extension to quantized settings.
  • Organizational and policy frameworks for “SLT-first” Green AI
    • Sector: policy, corporate sustainability
    • Application: Encourage procurement and engineering practices that prefer SLT-based pruning at initialization to cut training emissions; set targets for sparsity and width planning grounded in theory.
    • Tools/Products/Workflows: Governance policies, internal scorecards, external reporting standards referencing SLT guarantees.
    • Assumptions/Dependencies: Adoption depends on demonstrable cost and carbon benefits; requires change management and tooling maturity.
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Glossary

  • Attention heads: Parallel attention submodules within MHA that compute relationships separately and are combined in the output. "computes their pair-wise relationships at each of the HH attention heads"
  • Attention mask: A binary mask that restricts which positions an input token can attend to in the sequence. "we define a binary attention mask ai∈{0,1}⊤{\bm{a}_i \in \{0,1\}^\top}"
  • Attention mechanism: The component that computes relevance scores (e.g., via query-key inner products) to weight values for aggregation. "does an attention mechanism---an essential component of transformers---contain an SLT?"
  • Convolutional networks: Neural architectures using convolutional layers, previously analyzed under SLTH. "such as convolutional and equivariant networks"
  • Decoder models: Transformer modules that generate outputs autoregressively, often with causal masks. "including encoder~\citep{devlin2019bert} and decoder models~\citep{radford2019language}"
  • Encoder: Transformer module that processes input sequences (typically bidirectionally) for representation learning. "including encoder~\citep{devlin2019bert} and decoder models~\citep{radford2019language}"
  • Equivariant networks: Architectures whose outputs transform predictably under input symmetries. "such as convolutional and equivariant networks"
  • Fully-connected ReLU network: A feedforward network using dense layers with ReLU activations. "They proved the existence of SLTs in a fully-connected ReLU network."
  • Hadamard product: Element-wise multiplication of matrices or vectors. "“⊙\odot” represents an element-wise multiplication (\ie, the Hadamard product)."
  • i.i.d.: Independently and identically distributed random variables used for weight initialization. "each entry of $\tilde{\bm{W}_1$ and $\tilde{\bm{W}_2$ is drawn i.i.d. from U[−1,1]U[-1, 1]."
  • Inner product: The dot product used in attention to score query-key similarity. "the inner product between two vectors called query and key"
  • Key: A linear projection of inputs used with queries to compute attention scores. "the inner product between two vectors called query and key"
  • Lipschitz continuity: A property bounding how much a function’s output can change relative to input changes. "exploiting the 1-Lipschitz continuity of the softmax"
  • Lottery ticket hypothesis: The claim that overparameterized networks contain trainable sparse subnetworks. "The lottery ticket hypothesis~\citep{frankle2018the}---overparameterized networks contain subnetworks"
  • Multi-head attention (MHA): An attention mechanism using multiple heads to capture diverse relationships. "the multi-head attention (MHA) mechanism, a core component of transformers."
  • Overparameterized networks: Models with more parameters than strictly necessary, enabling hidden subnetworks. "overparameterized networks contain subnetworks that achieve comparable accuracy"
  • Query: A linear projection of an input that is matched against keys to compute attention scores. "single-layer projections for the query qi(j)\bm{q}_i^{(j)}, key K(j)\bm{K}^{(j)}, value V(j)\bm{V}^{(j)}"
  • Softmax: A normalization function converting scores to a probability distribution over attention weights. "The softmax function with the attention mask is defined as $\softmax(\cdot)$."
  • Spectral norm: The largest singular value of a matrix, used to measure operator norm. "We use the norm of matrices and vectors ∥⋅∥\|\cdot\| as the spectral norm unless otherwise specified by subscripts."
  • Strong lottery ticket hypothesis (SLTH): The conjecture that high-performing subnetworks exist at initialization without training. "The strong lottery ticket hypothesis (SLTH) conjectures that high-performing subnetworks, called strong lottery tickets (SLTs), are hidden in randomly initialized neural networks."
  • Strong lottery tickets (SLTs): Subnetworks identified at initialization that match trained model performance without weight updates. "subnetworks (called strong lottery tickets (SLTs)) that achieve comparable accuracy"
  • Subset-sum approximation: A combinatorial technique used to construct approximations via selective pruning. "introduced a subset-sum approximation technique~\citep{lueker1998exponentially} into the SLTH context"
  • Transformer: A neural architecture built on attention mechanisms, extended here under SLTH. "we extend the SLTH to transformers without normalization layers."
  • Two-layers-for-one approximation: Theoretical technique where two random layers are pruned to approximate one target layer. "This approach ... is called the two-layers-for-one approximation"
  • Union bound: A probability inequality used to bound the chance that any of several events fails. "a union bound guarantees that the approximation succeeds across all heads with probability at least 1−ϵ1 - \epsilon."
  • Value projection: A linear projection of inputs that are aggregated by attention weights to form outputs. "single-layer projections for the query qi(j)\bm{q}_i^{(j)}, key K(j)\bm{K}^{(j)}, value V(j)\bm{V}^{(j)}"
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Dice Question Streamline Icon: https://streamlinehq.com

Open Problems

We haven't generated a list of open problems mentioned in this paper yet.

Ai Sparkles Streamline Icon: https://streamlinehq.com Generate Now
List To Do Tasks Checklist Streamline Icon: https://streamlinehq.com

Collections

Sign up for free to add this paper to one or more collections.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up
X Twitter Logo Streamline Icon: https://streamlinehq.com

Tweets

This paper has been mentioned in 1 tweet and received 97 likes.

Upgrade to Pro to view all of the tweets about this paper:

Start a free 7-day Pro trial