Shorter but not Worse: Frugal Reasoning via Easy Samples as Length Regularizers in Math RLVR (2511.01937v1)

Published 2 Nov 2025 in cs.LG, cs.AI, and stat.ML

Abstract: LLMs trained for step-by-step reasoning often become excessively verbose, raising inference cost. Standard Reinforcement Learning with Verifiable Rewards (RLVR) pipelines filter out easy'' problems for training efficiency, leaving the model to train primarily on harder problems that require longer reasoning chains. This skews the output length distribution upward, resulting in a \textbf{model that conflatesthinking longer'' with ``thinking better''}. In this work, we show that retaining and modestly up-weighting moderately easy problems acts as an implicit length regularizer. Exposing the model to solvable short-chain tasks constrains its output distribution and prevents runaway verbosity. The result is \textbf{\emph{emergent brevity for free}}: the model learns to solve harder problems without inflating the output length, \textbf{ despite the absence of any explicit length penalization}. RLVR experiments using this approach on \textit{Qwen3-4B-Thinking-2507} (with a 16k token limit) achieve baseline pass@1 AIME25 accuracy while generating solutions that are, on average, nearly twice as short. The code is available at \href{https://github.com/MBZUAI-Paris/Frugal-AI}{GitHub}, with datasets and models on \href{https://huggingface.co/collections/MBZUAI-Paris/k2-think-mini-68dcfa8b114686a4bd3dc2bc}{Hugging Face}.

Summary

The paper demonstrates how retaining moderately easy math problems acts as an implicit length regularizer to reduce verbosity while preserving problem-solving accuracy.
It employs a two-stage training process with GRPO and curriculum learning on the DeepMath-103 dataset, yielding significant improvements in Efficiency-Adjusted Accuracy.
Experimental results show that Frugal-Math models achieve comparable reasoning performance with fewer tokens, illustrating enhanced computational efficiency.

Frugal Reasoning in Mathematical RLVR

Introduction

The paper "Shorter but not Worse: Frugal Reasoning via Easy Samples as Length Regularizers in Math RLVR" (2511.01937) discusses the optimization of LLMs trained for step-by-step reasoning, particularly focusing on reducing verbosity while maintaining problem-solving efficacy. Reinforcement Learning with Verifiable Rewards (RLVR) is leveraged in training these models, and the study highlights a unique approach where retaining moderately easy problems serves as an implicit length regularizer, thus addressing the skewed output length distribution observed in traditional training frameworks.

Background

Recent developments in LLMs have seen significant advancements in machine reasoning through test-time scaling. This involves producing extensive chains of thought which are effective on complex mathematical and coding tasks. However, this comes at the expense of verbosity, which increases inference latency and computational resource usage. Traditional RLVR pipelines filter out easy problems, directing the model to focus on medium-to-hard problems that require longer reasoning chains, inadvertently skewing the output length distribution upward.

The RLVR method typically filters easy problems for efficiency since they offer less learning signal under Group Relative Policy Optimization (GRPO). This incentivization leads models to associate longer reasoning chains with better performances, a bias also explained through information-theoretic perspectives, where verbosity lowers conditional entropy of the final prediction. Therefore, verbosity becomes a shortcut rather than an indicator of better reasoning.

Methodology

The authors propose a novel approach where moderately easy problems are retained and up-weighted during training.

Implicit Length Regularization: Retaining easy tasks and exposing the model to solvable short-chain tasks act as implicit length regularizers. This approach constrains the output distribution and prevents verbosity without explicit penalties.

Data Curation: The empirical success-rate analysis shows that token lengths vary systematically with difficulty. By skewing the dataset to include more easy problems, the reward signal emphasizes conciseness.

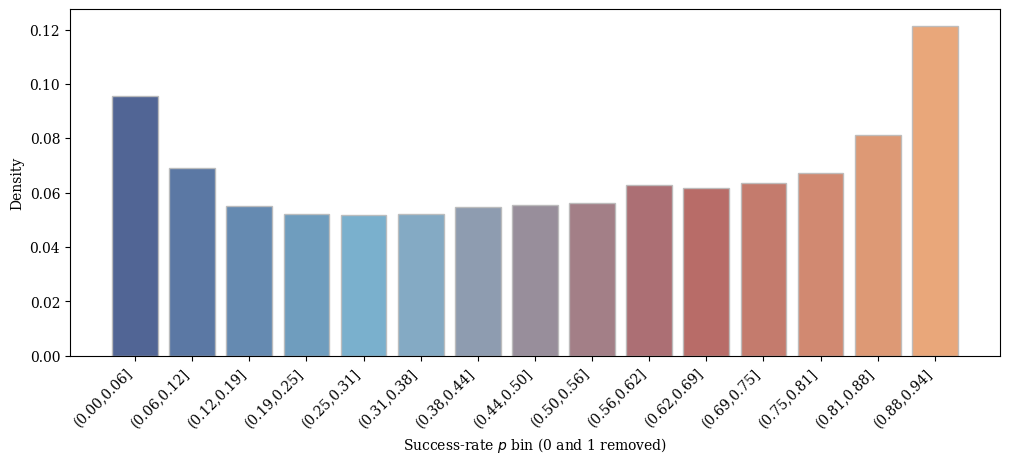
Figure 1: Token count distribution as a function of empirical success rate $p$ .

Curriculum RLVR: After achieving emergent brevity in Stage 1 through mixed difficulty batch sampling, Stage 2 involves a curriculum-based RLVR on a filtered subset of the DeepMath-103 dataset. This enriches the model's reasoning capabilities across wider mathematical domains while maintaining brevity.

Experimental Setup and Results

The experiment fine-tunes the Qwen3-4B-Thinking-2507 model with GRPO on curated mathematical datasets and evaluates it across benchmarks such as AIME25, GSM-Plus, and Omni-Hard. The two-stage training results show significant improvements in average accuracy and Efficiency-Adjusted Accuracy (EAA), with Frugal-Math models outperforming larger counterparts in terms of token efficiency.

Figure 2: Average response length.

Performance Analysis: The findings indicate that Frugal-Math-4B models efficiently solve complex reasoning tasks while maintaining concise outputs, proving beneficial under tight output constraints. This showcases their superiority in maintaining accuracy with significantly fewer tokens compared to the base model and larger baselines.

Figure 3: Scaling behavior under varying generation budgets (8 k â 16 k â 32 k â 42 k). The top panels show Pass@1 accuracy and the bottom panels show Efficiency-Adjusted Accuracy for the three benchmarks; AIME25, GSM Plus, and Omni-Hard.

Conclusion

This paper illustrates that retaining moderately easy problems as length regularizers not only reduces verbosity but also improves accuracy and efficiency in mathematical reasoning tasks. The implications on training data—emphasizing its curation—are profound in shaping reasoning models’ efficiency. Future work could explore adaptive curricula across other domains and integrate explicit length penalties alongside these implicit techniques for finer brevity control.