Deep sequence models tend to memorize geometrically; it is unclear why (2510.26745v1)
Abstract: In sequence modeling, the parametric memory of atomic facts has been predominantly abstracted as a brute-force lookup of co-occurrences between entities. We contrast this associative view against a geometric view of how memory is stored. We begin by isolating a clean and analyzable instance of Transformer reasoning that is incompatible with memory as strictly a storage of the local co-occurrences specified during training. Instead, the model must have somehow synthesized its own geometry of atomic facts, encoding global relationships between all entities, including non-co-occurring ones. This in turn has simplified a hard reasoning task involving an $\ell$-fold composition into an easy-to-learn 1-step geometric task. From this phenomenon, we extract fundamental aspects of neural embedding geometries that are hard to explain. We argue that the rise of such a geometry, despite optimizing over mere local associations, cannot be straightforwardly attributed to typical architectural or optimizational pressures. Counterintuitively, an elegant geometry is learned even when it is not more succinct than a brute-force lookup of associations. Then, by analyzing a connection to Node2Vec, we demonstrate how the geometry stems from a spectral bias that -- in contrast to prevailing theories -- indeed arises naturally despite the lack of various pressures. This analysis also points to practitioners a visible headroom to make Transformer memory more strongly geometric. We hope the geometric view of parametric memory encourages revisiting the default intuitions that guide researchers in areas like knowledge acquisition, capacity, discovery and unlearning.
Summary
- The paper demonstrates that deep sequence models develop geometric memory, allowing them to synthesize global structure for implicit multi-hop reasoning.
- The paper uses a path-star graph task to reveal that models trained in the in-weights regime achieve near-perfect accuracy even on unseen nodes.
- The paper analyzes embedding geometry and spectral bias, challenging the traditional associative memory view and suggesting new directions for model design.
Geometric Memorization in Deep Sequence Models: Empirical Phenomena and Theoretical Challenges
Introduction
This paper investigates the nature of parametric memory in deep sequence models, particularly Transformers and Mamba, by contrasting two paradigms: the traditional associative memory view, where models store local co-occurrences as a lookup table, and a geometric memory view, where models synthesize global relationships between entities in their embedding space. The authors present empirical evidence that, even in tasks designed to be adversarial to next-token learning, deep sequence models can develop geometric representations that encode global structure, enabling efficient implicit reasoning. This phenomenon is not easily explained by standard architectural, optimization, or capacity-based arguments, and the paper explores its origins, implications, and limitations.
Experimental Setup: Path-Star Graph Reasoning
The core experimental paradigm is the path-star graph task, which is designed to be challenging for next-token prediction models. In the in-context version, the model is given a serialized adjacency list of a randomly labeled path-star graph and must predict the unique path from the root to a specified leaf. Prior work has shown that Transformers and Mamba fail on this task due to the emergence of "Clever Hans" shortcuts and the computational hardness of learning multi-hop compositions without intermediate supervision.
In contrast, the in-weights version fixes a single path-star graph and trains the model to memorize its edges (local associations) and, for a subset of leaves, to output the full path from the root to the leaf. The model is then evaluated on held-out leaves.
Figure 1: Overview of in-context path-star task, where the model receives a randomized adjacency list and must predict the path to a goal node.
Figure 2: Overview of in-weights path-star task, where the model memorizes the graph's edges and is trained to output paths for a subset of leaves.
Empirical Findings: Success of Geometric Memory
The main empirical result is that both Transformers and Mamba, when trained in the in-weights regime, achieve perfect or near-perfect accuracy on path-finding tasks in large path-star graphs (up to nodes), even when tested on unseen leaves. This is in stark contrast to the in-context regime, where models fail to generalize.
Figure 3: Success of Transformer in in-weights path-star task, achieving high accuracy on large graphs.
Figure 4: Failure of Transformer in in-context path-star task, with accuracy at chance level.
A key observation is that the hardest token—the first decision in the path—can be learned in isolation, without intermediate supervision, in the in-weights regime. This is theoretically surprising: under the associative memory view, this requires an -fold composition of local associations, which is known to be computationally hard for gradient-based learners. Empirically, models with frozen embeddings (i.e., forced to use only associative memory) fail at this task, supporting the claim that geometric memory is essential for success.
Analysis of Embedding Geometry
The authors analyze the learned embeddings and find that they exhibit global geometric structure: nodes along the same path are clustered in embedding space, and the dot product between embeddings reflects multi-hop proximity, even for non-adjacent nodes. This is visualized via cosine similarity heatmaps and dimensionality reduction projections.
Figure 5: Associative vs. geometric memory. Left: associative memory stores co-occurrences in a weight matrix with arbitrary embeddings. Middle: learned embeddings reflect global structure. Right: Node2Vec, which prohibits associative memory, yields even more elegant geometry.
Figure 6: Edge-memorized and full-path-trained embedding heatmap, showing strong alignment between leaf and first-hop embeddings within each path.
Figure 7: UMAP projection of token embeddings, revealing clear path-star topology in the learned geometry.
The geometric memory paradigm enables the model to reduce a multi-hop reasoning task to a single geometric lookup, explaining the empirical success in the in-weights regime.
Theoretical Challenges: Why Does Geometry Prevail?
A central question is why geometric memory emerges, given that both associative and geometric solutions are equally valid for fitting the training data. The authors systematically rule out several standard explanations:
- Capacity Pressure: Geometric memory is not always more succinct than associative memory in terms of bit or norm complexity, especially in memorization tasks without statistical redundancy.
- Architectural or Optimization Bias: The same architectures can learn associative memory if embeddings are frozen, indicating no explicit architectural prohibition.
- Supervisory Pressure: Global geometry emerges even when training is restricted to local edge memorization, without explicit global supervision.
The authors connect the emergence of geometry to spectral bias in Node2Vec-style models, where embeddings align with the top eigenvectors (Fiedler vectors) of the graph Laplacian. Empirically, Node2Vec yields even cleaner geometric structure than Transformers, suggesting that Transformers' memory is a mixture of geometric and associative components.
Figure 8: Fiedler(-like) vector of the graph, encoding global structure that mirrors Node2Vec embeddings.
Spectral Bias in Node2Vec and Implications for Transformers
The paper provides an empirical analysis of the training dynamics in Node2Vec, showing that embeddings converge to the span of the graph's Fiedler vectors, and the coefficient matrix's null space aligns with these vectors. This spectral bias arises without explicit low-rank constraints, regularization, or multi-hop supervision, and is robust across graph topologies.
(Figure 9, 17, 18, 19)
Figure 9: Tiny path-star; Figure 10: Tiny grid; Figure 11: Tiny cycle; Figure 12: Tiny irregular graph. All show emergence of geometric memory across architectures and graph types.
The implication is that spectral properties of the graph and the training dynamics naturally induce geometric memory, even in the absence of explicit pressures. However, in deep sequence models, associative memory remains a competitor, and the conditions under which geometric memory dominates are not fully understood.
Practical and Theoretical Implications
- Retrieval and Reasoning: Geometric memory enables efficient multi-hop reasoning and may support combinatorial generalization and creativity by encoding global relationships.
- Knowledge Editing and Unlearning: The interdependence of geometric memory may complicate targeted editing or unlearning of specific facts.
- Model Design: There is visible headroom to make Transformer memory more geometric, potentially by architectural modifications or training objectives inspired by Node2Vec.
- Interpretability and World Models: The geometric view provides a new lens for analyzing model representations, interpretability, and the emergence of "world models" in LLMs.
Limitations and Open Questions
- The positive results are demonstrated on symbolic tasks and specific graph topologies; generalization to natural language and more complex structures is not established.
- Theoretical understanding of the competition between associative and geometric memory in deep networks remains open.
- The disentanglement of geometric and associative memory in multi-layer architectures is not well-defined.
Conclusion
This work demonstrates that deep sequence models, when trained to memorize atomic facts, often develop geometric representations that encode global structure, enabling efficient implicit reasoning. This geometric memory emerges even in the absence of explicit architectural, optimization, or supervisory pressures, and is best explained by a naturally occurring spectral bias. The findings challenge the sufficiency of the associative memory paradigm and open new directions for understanding, designing, and interpreting deep sequence models. Future work should aim to formalize the conditions under which geometric memory prevails, extend these insights to natural language tasks, and explore architectural innovations that promote desirable geometric properties in model memory.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper looks at how deep sequence models (like Transformers) store facts they’ve learned. Most people imagine these models keeping a giant “lookup table” of which things appear together (associative memory). The authors show a different picture: the models often build a kind of internal “map” where related things are placed near each other in space (geometric memory). This geometric map lets the model solve problems that would be very hard if it only used a simple lookup table.
What questions did the researchers ask?
In simple terms, they asked:
- Do models store facts as a flat list of pairings (“A goes with B”), or as points arranged in space so that distance and direction capture deeper relationships?
- Can this geometric kind of memory help models “reason” over many steps, even when they were only trained on local, one-step facts?
- Why would a neat geometry appear at all, especially when it’s not obviously simpler than a lookup table?
- Can we explain this geometry by looking at a simpler model (Node2Vec) and a general tendency called spectral bias (a preference for smooth, simple patterns)?
How did they paper it?
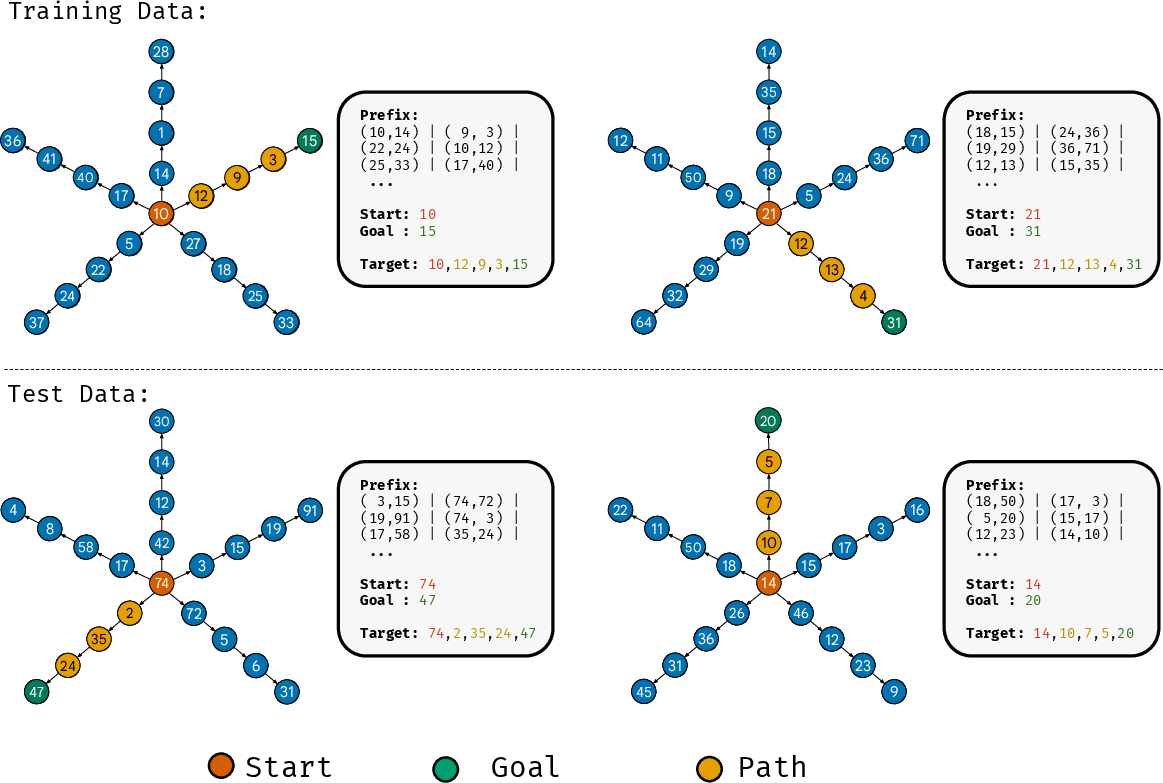
They designed a clean, controlled test using a special kind of graph (think: a map of dots and lines) called a path-star graph.
- Picture a “hub-and-spokes” shape: one central root node with several long, straight paths (“spokes”) sticking out. Each spoke is the same length, with a “leaf” node at the end.
They compared two setups:
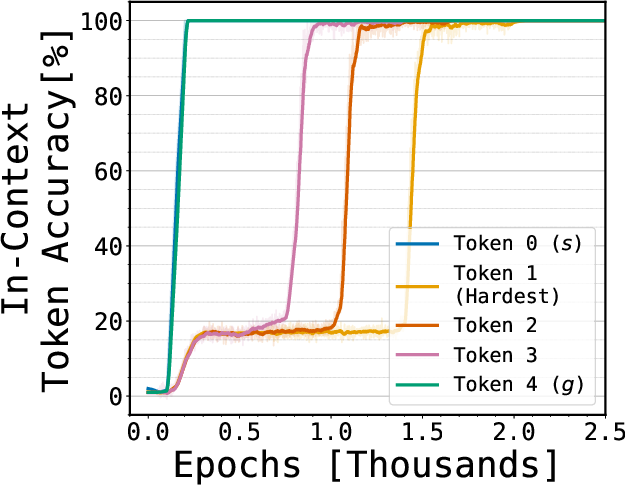
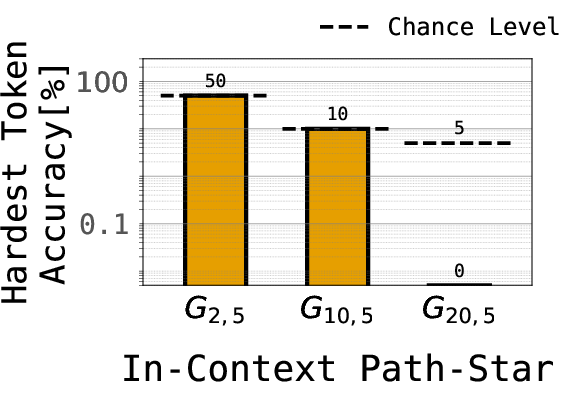
1) In-context version (the older test): - Each example gives the model the entire graph as text right before the question, then asks: “From this leaf, what is the path back to the root?” - Many models fail here because they latch onto easy tricks and never learn the true planning logic.
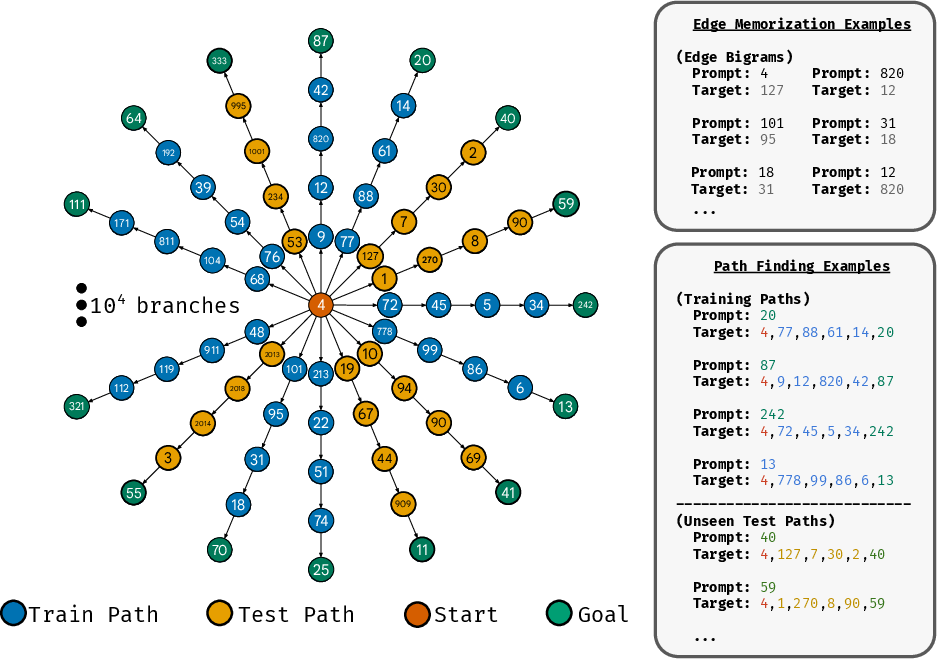
2) In-weights version (the new test in this paper): - The model is shown many short examples of connected pairs (edges like “X is next to Y”). It must memorize the whole graph in its weights (its “brain”) instead of being shown the graph each time. - Then it’s asked to find full paths from leaf to root for new leaves it wasn’t directly trained on. - They also tried a harder twist: train on edges plus only the first step of the path (the hardest part), not the full path step-by-step.
They ran this with standard models (Transformers) and a newer sequence model (Mamba), and also looked at a simpler embedding method called Node2Vec to understand why a geometry might form.
Key terms in everyday language:
- Edge memorization: learn which dots are directly connected.
- Path finding: figure out the whole route back to the center from a leaf, which takes many steps.
- First-token-only training: only teach the model the first hop; no “step-by-step” hints for later hops.
- Embeddings: the positions of items (like nodes) in the model’s internal space.
- Geometric memory: the idea that the positions themselves encode useful global structure.
- Associative memory: the idea of just storing “who co-occurs with whom” like a big table.
- Spectral bias: a natural tendency to prefer smooth, simple patterns across a network—like how a vibrating string first uses simple waves.
What did they find, and why does it matter?
Here are the main results, with plain-language explanations:
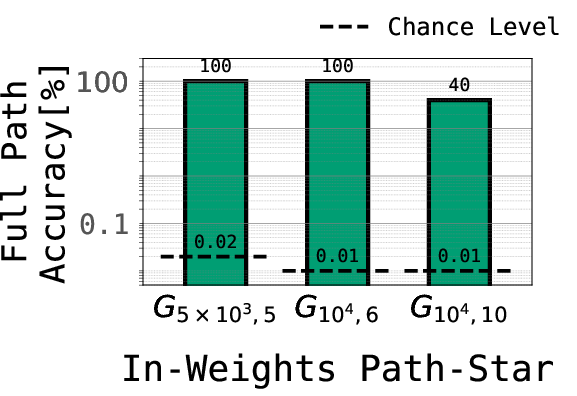
- Models succeed at multi-step reasoning when facts are stored in their weights.
- In the in-weights version, Transformers and Mamba learned to find paths on very large graphs (tens of thousands of nodes), even for new leaves they hadn’t been directly trained on. This is impressive because it’s a long, multi-step task.
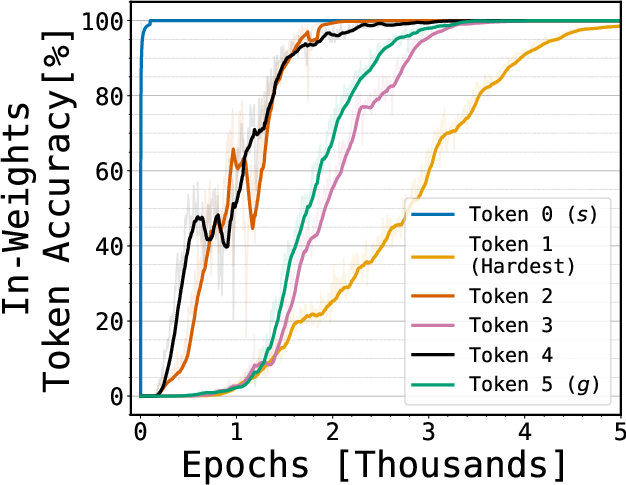
- The “hardest step” can be learned in isolation.
- The first hop from a leaf is the toughest because it usually needs many steps of thinking. If the model only had an associative lookup, learning that final answer would require composing many little lookups—something gradient-based learning is known to struggle with.
- Yet the models learned this first hop well even when trained only on that hop, with no step-by-step guidance. That suggests they’re not just composing lots of local lookups; they’re using a smarter structure.
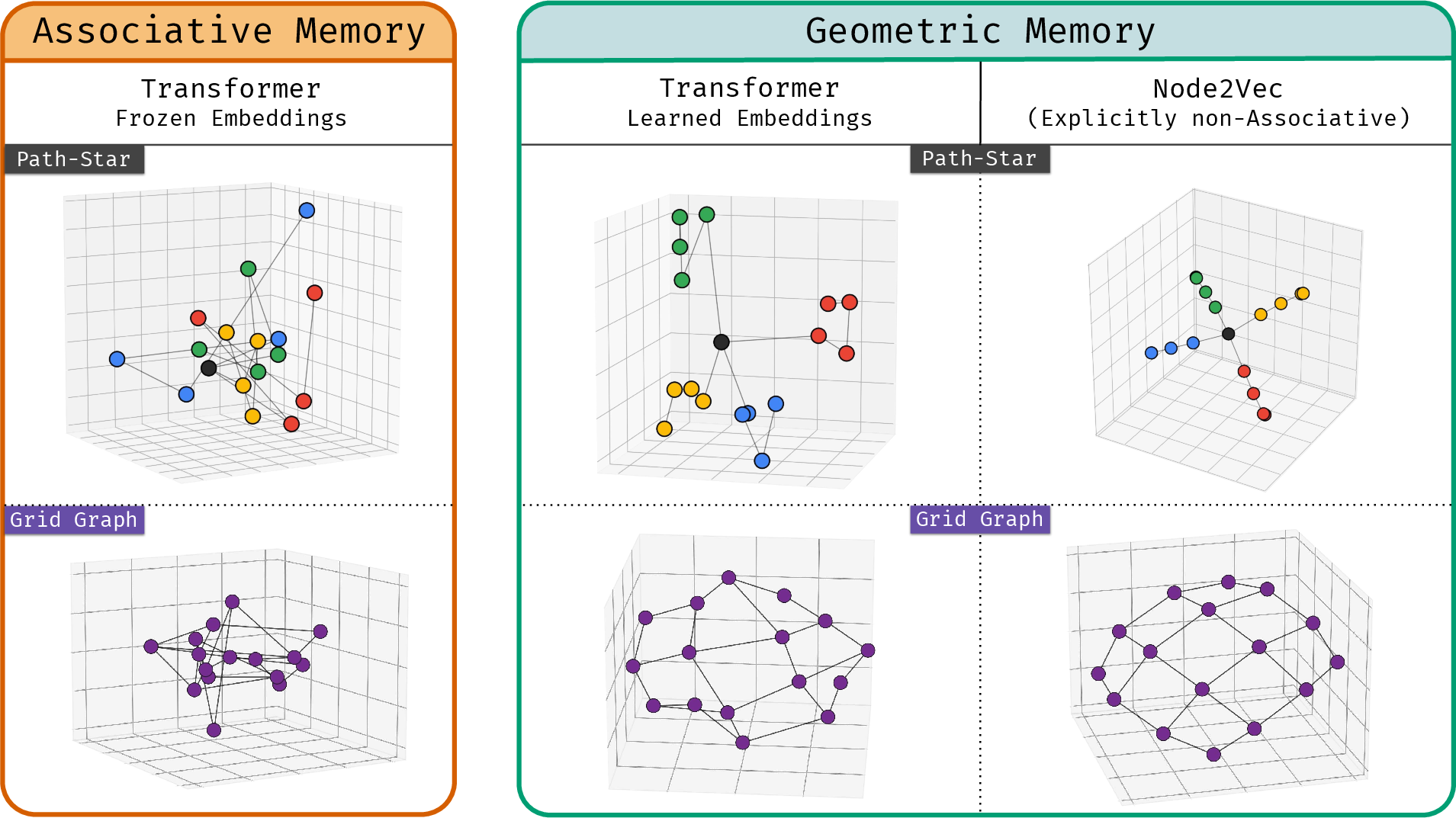
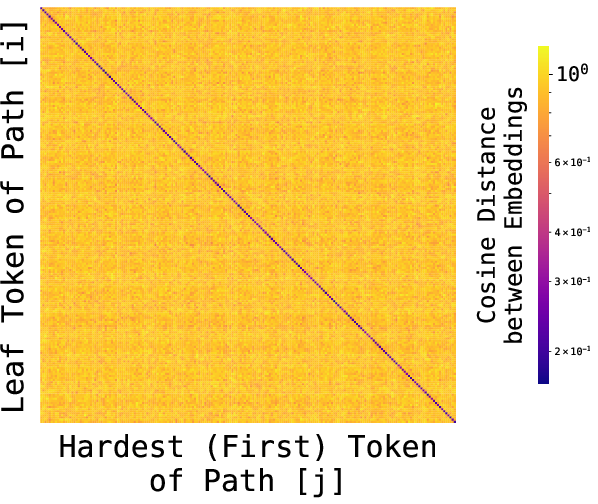
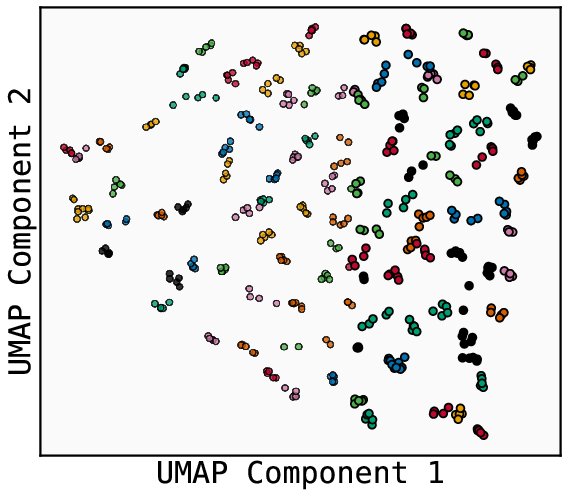
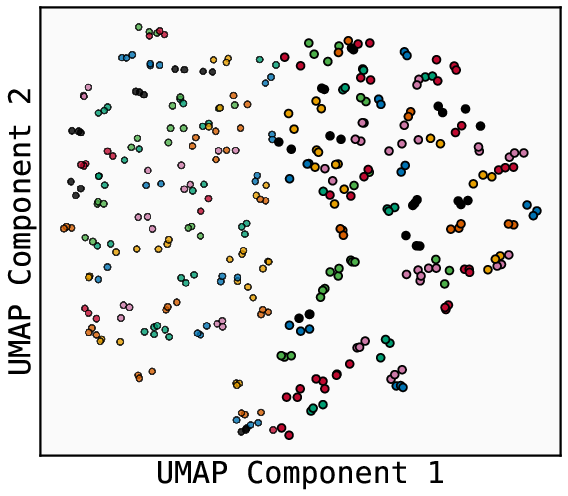
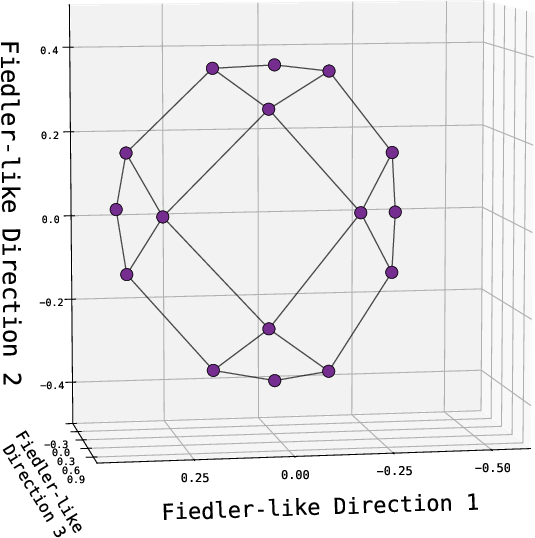
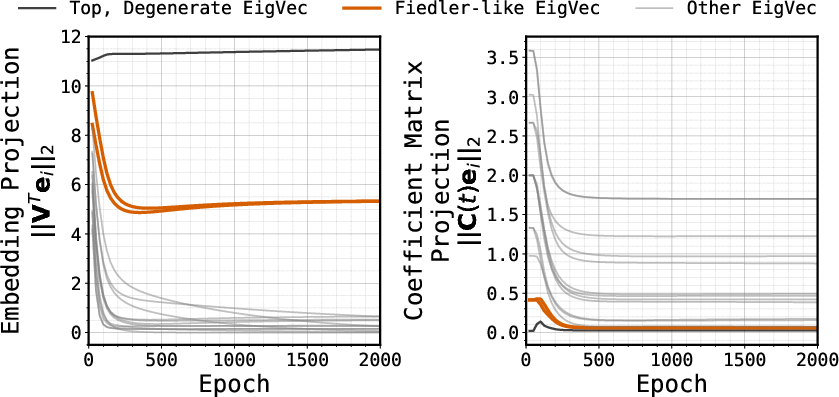
- The model’s embeddings look like a map, not a phone book.
- When the authors visualize the learned embeddings, nodes from the same spoke cluster together. Leaves and their correct first-hop neighbors are close in the model’s space. That means the model built a global geometry: even pairs that never appeared together during training still end up in meaningful positions.
- It’s not simply because of “extra help” in training.
- The geometry appears even when the model is trained only on local edge pairs (no path-finding supervision). So the “global” structure emerges from many local facts.
- The success isn’t explained by the model “peeking ahead” using later tokens’ feedback, either—the learning pattern doesn’t match that.
- It’s not obviously due to size limits or simplicity pressures.
- One might think the model chose geometry because it uses fewer parameters than a big lookup. But the authors argue that in this specific task, a geometric representation is not clearly more compact than a lookup—the difference can be tiny.
- They also show you can force a pure associative solution (by freezing embeddings) with the same architecture. So geometry is not the only available path. Yet when allowed, the model still tends to learn geometry.
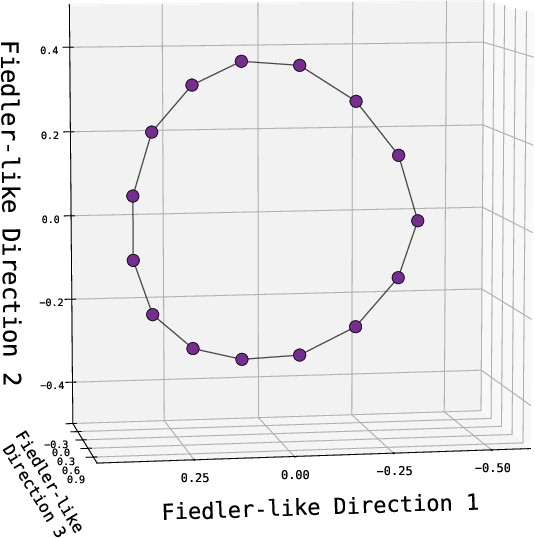
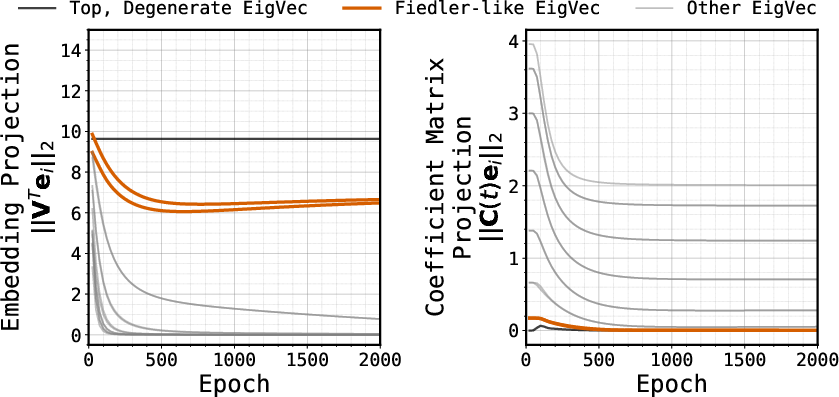
- A clue from a simpler model: Node2Vec and spectral bias.
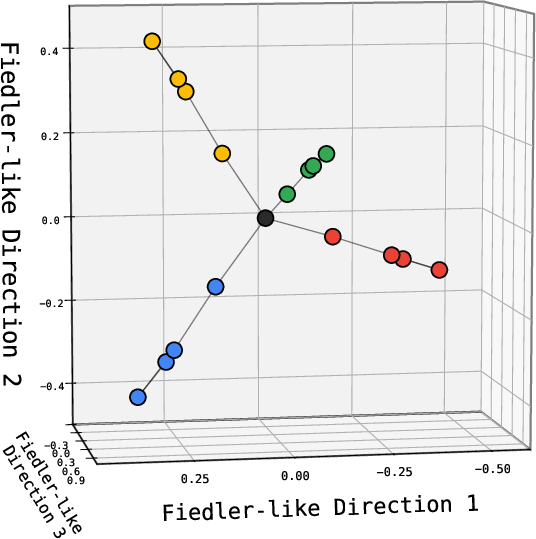
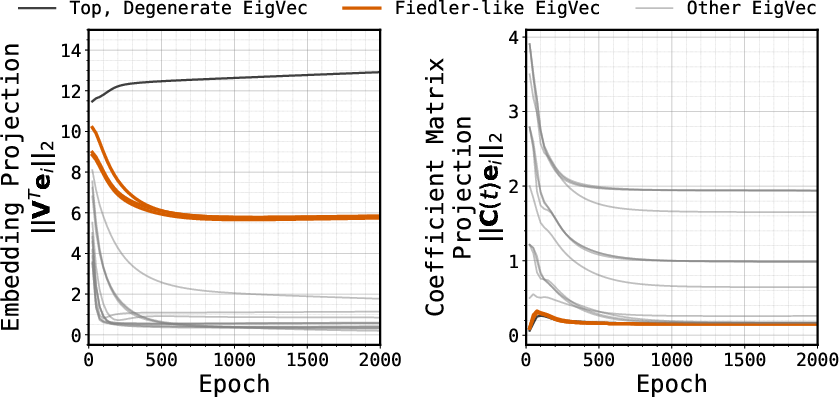
- Node2Vec, a classic embedding method trained only on local connections, often produces embeddings that match the smoothest global patterns in a graph (mathematically, top eigenvectors of the graph Laplacian—think “the simplest ways to color the graph smoothly”).
- This “spectral bias” explains why a global, elegant geometry can arise from only local facts.
- The authors find Node2Vec’s geometry can be even cleaner than the Transformer’s, suggesting there’s “headroom” to make Transformer memory more strongly geometric and less like a jumble of local lookups.
Why this matters:
- If models naturally build geometric maps from local facts, they can solve multi-step problems more easily and generalize better across the graph, even without step-by-step training.
- This challenges the common mental model that large models mostly memorize using association tables. They often build structured representations instead.
What could this change in practice?
- Better reasoning without step-by-step hints:
- Encouraging more geometric memory could help LLMs do more “implicit reasoning” (solving multi-step tasks silently) by relying on their internal maps.
- More creative connections:
- Geometric memory captures global relationships. That could help models connect distant ideas more flexibly, potentially aiding discovery and creativity.
- Trade-offs for editing and unlearning:
- If facts are woven into a global map, removing one fact may affect others nearby in that map. That could make precise editing or unlearning harder.
- Rethinking retrieval systems:
- In search and retrieval, people use both “generative” models and simpler dual-encoder models. The geometry insights here could guide when a simpler geometric approach (like Node2Vec-style embeddings or dual encoders) might be better.
- Open research questions:
- When and why does geometric memory beat associative memory during training?
- How can we shape training so geometry emerges more strongly and reliably in big LLMs?
- How do these internal maps relate to “world models” and shared representations across different models?
In short, the paper shows that deep sequence models often don’t just memorize who-goes-with-who. They build internal maps that capture the big picture. This geometry helps them think over many steps, even when they only saw local facts—and it points to new ways to make models reason better.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored in the paper. Each item is phrased for actionable follow-up by future researchers.
- Lack of a formal theory explaining why gradient-based training in deep sequence models (Transformers, Mamba) naturally yields global geometric memory from strictly local co-occurrence supervision; characterize optimization dynamics and conditions under which geometric memory outcompetes associative memory.
- Absence of quantitative diagnostics to distinguish and track “geometric” vs “associative” parametric memory during training; define robust metrics (e.g., spectral alignment to graph Laplacian eigenvectors, multi-hop distance fidelity, geometry–associativity mixture coefficients) and their reliability across architectures.
- Unverified extent of spectral bias in Transformers/Mamba: do their learned embeddings quantitatively align with Laplacian eigenvectors (Fiedler vectors) across graph families and scales? Develop causal tests disentangling spectral geometry from associative components.
- Unclear minimal training recipe for geometric emergence: identify necessity/sufficiency of reverse-edge augmentation, pause tokens, formatting choices, and interleaving edge-memorization with path-finding; determine if geometry persists without these aids.
- Missing rigorous link between the in-weights first-token learning and composition hardness results: formally show when associative lookup requires exponential-time learning while geometric memory reduces the complexity to O(1), and prove task-specific lower/upper bounds.
- Incomplete capacity analysis: generalize or refute the claim that geometric and associative memories are equally succinct (bit/norm complexity) beyond path-star/cycle graphs, including weight tying, normalization, weight decay, and different graph degrees/path lengths.
- Unknown scalability limits: characterize how performance and geometry degrade with increasing graph size, degree, and path length; identify thresholds as functions of model size, depth, embedding dimension, and training budget.
- Limited evidence beyond synthetic graphs: test whether similar geometric memory arises in natural language pretraining and tasks (knowledge recall, multi-hop QA, compositional generalization), and quantify multi-hop relational encoding among real-world entities.
- Undefined practical levers to strengthen geometric bias in Transformers: propose and evaluate architectural/training modifications (e.g., Laplacian-informed regularization, contrastive/objective shaping, embedding parameterization, attention constraints) and measure trade-offs in recall, inference speed, and editability.
- Unexplored interaction with in-context learning: under what conditions does parametric geometric memory outperform in-context reasoning, and can curriculum, pre-caching gradients, or supervision designs be tuned to consistently favor geometric representations?
- Unaddressed consequences for knowledge editing and unlearning: analyze how interdependent geometric storage impacts targeted fact edits, collateral changes, retrieval precision, and stability; design geometry-aware editing/unlearning algorithms.
- Retrieval system implications not tested: compare generative retrieval vs dual-encoder methods on geometric memory strength, spectral alignment, and multi-hop reasoning; evaluate impacts on indexing, latency, and robustness in large-scale retrieval benchmarks.
- Node2Vec theory gap: provide a precise characterization of Node2Vec embeddings and dynamics without assuming typical pressures (e.g., windowing, negative sampling biases), and prove convergence to Laplacian spectra across diverse graphs and hyperparameters.
- “Adulteration” hypothesis unvalidated: quantify and experimentally verify that Transformer representations mix geometric and associative components; use interventions (embedding freezing, layer ablations, residual pathway manipulation) to measure mixture proportions and their effect on reasoning.
- Robustness not characterized: assess sensitivity of the learned geometry to node relabelings, edge noise, adversarial distractors, graph topology shifts, and random seeds; define stability scores and failure modes.
- Training mix effects underexplored: systematically paper whether interleaving vs staged training (edge-memorization then hardest-token finetuning) consistently induces geometry on unseen paths and generalizes to other graph topologies (tree-star, cycles, expanders).
- Tokenization and formatting uncertainty: determine how token granularity, pause tokens, and sequence formatting impact geometric emergence; identify formatting-invariant recipes to avoid brittle dependence on presentation details.
- Directionality requirements unclear: establish when single-direction edge supervision suffices to induce geometry at scale, and when bidirectional augmentation is necessary (reversal curse mitigation vs geometric formation).
- Benchmarking and evaluation gaps: standardize datasets and protocols for implicit in-weights reasoning beyond path-star (e.g., tree-star, cycles, expanders), including per-token learning order, first-token-only accuracy, spectral alignment metrics, and geometry visualization tooling.
- Theoretical limits of spectral geometry: identify graph families where Laplacian eigenvectors provide poor inductive biases for the reasoning objective; investigate alternative geometric priors (nonlinear manifolds, diffusion embeddings) and the role of positional encodings.
Practical Applications
Immediate Applications
Below are applications that can be deployed with existing tools and workflows, guided by the paper’s findings on geometric (global) parametric memory and implicit in-weights reasoning.
Industry
- Geometric retrieval and re-ranking (software, search, recommender systems)
- Use case: Replace multi-hop symbolic matching with one-step geometric scoring that captures multi-hop closeness between items/documents/entities.
- Tools/products/workflows:
- Geometric Retrieval Re-Ranker layered atop a dual-encoder or generative retrieval system; score candidates via dot products in a geometry aligned to graph structure.
- Embedding Geometry Monitor (heatmaps, cosine affinity matrices, UMAP) to audit whether embeddings encode global relationships (as in the paper’s path-star heatmaps).
- Assumptions/dependencies: Requires access to a domain graph or co-occurrence signal to train local edge-memorization; relies on spectral bias to form global geometry; may need reverse-edge augmentation and interleaved training (edge + path) for stability at scale.
- In-weights domain graph fine-tuning for enterprise knowledge (software, enterprise knowledge management)
- Use case: Fine-tune LLMs on edge-memorization of internal knowledge graphs (products, customers, support tickets) so the model performs implicit reasoning without a long context window.
- Tools/products/workflows:
- Geometric Memory Fine-Tuning Kit: interleave edge-memorization with first-token-only path objectives; include pause tokens and reverse edge augmentation to avoid “reversal curse.”
- Assumptions/dependencies: Nodes must be tokenizable; performance depends on embedding dimension, graph size, and training stability; the approach encodes global relationships implicitly, which can complicate subsequent editing/unlearning.
- Fraud ring and threat path detection (finance, cybersecurity)
- Use case: Train models on local transaction or event edges; leverage geometric embeddings to score likely multi-hop fraud/threat paths in a single step.
- Tools/products/workflows:
- One-Hop Planner: compute the most probable predecessor/successor via geometric proximity rather than iterative multi-hop simulation.
- Assumptions/dependencies: Requires reliable local supervision (edges); careful evaluation to avoid false positives stemming from geometric generalization to non-co-occurring entities.
- Logistics and network routing (robotics, transportation, energy)
- Use case: Replace multi-step planning on large networks (warehouse paths, road networks, power grids) with geometric first-step decision policies that internalize the global topology.
- Tools/products/workflows:
- Embedding-based Router: learn embeddings from local adjacency and deploy one-step neighbor selection for route initiation; empirically effective on large path-star-like topologies.
- Assumptions/dependencies: The target topology must be reasonably static during deployment; embeddings should be periodically refreshed when topology changes.
- Creative discovery and ideation (marketing, R&D, product strategy)
- Use case: Find non-obvious connections between concepts scattered across large corpora using global geometric proximity (combinational creativity).
- Tools/products/workflows:
- Creative Linker: suggest novel associations by ranking items that are geometrically “close” despite no explicit co-occurrence.
- Assumptions/dependencies: Works best when trained on broad, diverse corpora; must guard against spurious associations and ensure human-in-the-loop validation.
Academia
- Benchmarking implicit in-weights reasoning (machine learning research)
- Use case: Establish standard in-weights reasoning benchmarks (path-star, tree-star, cycle graphs) to evaluate geometric vs associative memory across architectures.
- Tools/products/workflows:
- Benchmark Suites with per-token accuracy curves, first-token-only tasks, and geometry audits (heatmaps, spectral alignment checks).
- Assumptions/dependencies: Synthetic benchmarks need careful scaling; ensure models cannot exploit left-to-right “Clever Hans” cheats.
- Interpretability via geometry audits (AI interpretability)
- Use case: Systematically measure the strength of geometric memory using cosine affinity matrices and spectral analyses; detect associative “contamination.”
- Tools/products/workflows:
- Embedding Geometry Monitor; spectral alignment tests against graph Laplacian eigenvectors (Fiedler vectors).
- Assumptions/dependencies: Requires instrumentation to extract token embeddings; depends on access to training data and model internals.
Policy and Governance
- Risk audits for unintended inference (AI safety, model governance)
- Use case: Assess whether a model’s geometric memory infers relationships between non-co-occurring entities, affecting privacy or compliance.
- Tools/products/workflows:
- Policy Audit Toolkit: probe models for inference leaps using controlled graph tasks; document geometric interdependencies that complicate “right to be forgotten.”
- Assumptions/dependencies: Evidence from synthetic tasks generalizes partially; additional domain-specific studies may be needed for sensitive deployments.
Daily Life
- Personal knowledge management with geometric linking (productivity software)
- Use case: Embed notes and references with local links; exploit emergent global geometry to surface multi-hop relationships for better recall and planning.
- Tools/products/workflows:
- PKM apps integrating geometric embeddings; visual “map of ideas” that highlights global proximity beyond direct links.
- Assumptions/dependencies: Users must provide local associations (tags, hyperlinks); geometry formation depends on app’s training and update cadence.
Long-Term Applications
These opportunities require further research, scaling, or development—especially around strengthening spectral geometry in Transformers and establishing robust workflows for editing/unlearning in geometric memory.
Industry
- Spectral regularization modules for LLMs (software, model engineering)
- Use case: Integrate Node2Vec-inspired spectral bias into Transformers to strengthen global geometry and reduce associative contamination.
- Tools/products/workflows:
- Spectral Regularization Layer: losses that encourage alignment with graph Laplacian eigenvectors; architectural tweaks that favor geometric storage.
- Assumptions/dependencies: Needs careful design to avoid over-constraining representations; may trade off some local recall performance.
- Geometric-aware knowledge editing/unlearning (software, compliance tooling)
- Use case: Develop surgical edit methods that account for the ripple effects in geometric memory when removing or revising facts.
- Tools/products/workflows:
- Unlearning Impact Analyzer: simulate how deleting an edge or entity changes global geometry; propose minimal edits that preserve downstream behavior.
- Assumptions/dependencies: Requires principled models of dependency propagation in embeddings; may need new optimizer strategies.
- Domain-specific implicit planners (robotics, operations research)
- Use case: Train planners that rely on in-weights geometry to make robust first-step decisions in dynamic, large-scale environments (autonomous driving, smart grids).
- Tools/products/workflows:
- Hybrid Geometric-Planner Architectures: combine geometric first-step policies with explicit search/planning when necessary.
- Assumptions/dependencies: Must address safety and distribution shift; requires online adaptation when topology changes frequently.
- Generative retrieval vs dual-encoder selection frameworks (software, IR systems)
- Use case: Decision tools that compare geometric strength and task fit across generative retrieval and dual-encoders, informed by the paper’s headroom findings.
- Tools/products/workflows:
- Retrieval Architecture Advisor: measures geometry quality, spectral alignment, and downstream metrics to recommend system design.
- Assumptions/dependencies: Requires standardized evaluation suites; business constraints (latency, cost) will shape recommendations.
Academia
- Foundations of geometric vs associative competition under gradient descent (theory, optimization)
- Use case: Understand when and why geometric memory wins despite equal or higher succinctness, and how implicit/explicit pressures shape embeddings.
- Tools/products/workflows:
- New theory linking training dynamics to spectral emergence without standard capacity pressures; controlled experiments with frozen embeddings, different losses, and curricula.
- Assumptions/dependencies: Complex dependence on initialization, optimizer, architecture; results may vary across tasks and scales.
- Robust implicit reasoning in natural language (NLP benchmarks and models)
- Use case: Extend geometric memory insights from symbolic tasks to real-world NLP (multi-hop QA, compositional reasoning), where results have been mixed.
- Tools/products/workflows:
- Benchmarks that isolate geometric gains (e.g., first-token decision tasks in text); training protocols emphasizing local supervision with global evaluation.
- Assumptions/dependencies: Success depends on mapping textual signals to graphs or latent topologies; requires careful task design to avoid shortcuts.
- Interpretability of “Platonic representations” via geometric nuclei (AI interpretability)
- Use case: Test the hypothesis that different models converge to similar geometric cores (Platonic representations), facilitating transfer and alignment.
- Tools/products/workflows:
- Cross-model geometry comparison tools; analysis of linear features and superposition in large-scale LMs via graph-derived nuclei.
- Assumptions/dependencies: Requires multi-model access; standardization of representation comparison methods.
Policy and Governance
- Standards for memory transparency and editability (AI regulation)
- Use case: Develop guidelines and audits that account for geometric interdependencies in parametric memory—implicating consent, privacy, and unlearning.
- Tools/products/workflows:
- Regulatory frameworks specifying geometry-aware testing; documentation of learned global relations and their edit costs.
- Assumptions/dependencies: Needs consensus on measurement methodologies; may require sector-specific norms (healthcare, finance).
- Safety controls for combinational creativity (AI safety, content governance)
- Use case: Guardrails around models that discover novel connections across large corpora, to manage misinformation, bias amplification, or IP concerns.
- Tools/products/workflows:
- Creativity Risk Assessments: evaluate outputs linked by geometric closeness but lacking explicit evidence; require provenance tracking and human review.
- Assumptions/dependencies: Balancing innovation with risk mitigation; depends on robust detection of spurious geometric links.
Daily Life
- Offline geometric navigation and planning assistants (consumer software, mobility)
- Use case: Personal devices that pre-memorize local maps/graphs and provide fast, low-power route suggestions via embedding geometry.
- Tools/products/workflows:
- Lightweight Geometric Navigator: periodic on-device training from locally observed edges; one-step decision policies for route initiation.
- Assumptions/dependencies: Requires on-device training capability and periodic updates; must handle changes in topology gracefully.
- Geometric personal AI that resists context overload (consumer AI)
- Use case: Assistants that rely more on parametric geometric memory than on large context windows, improving latency and usability.
- Tools/products/workflows:
- Geometry-first Personal Models: local edge logging (contacts, tasks, locations), implicit reasoning over multi-hop relationships in daily routines.
- Assumptions/dependencies: Privacy controls and data minimization; clear UX for editability and transparency.
Glossary
- associative view: An abstraction where a model stores local co-occurrences via a weight matrix rather than organizing embeddings geometrically. "We contrast this associative view against a geometric view of how memory is stored."
- chain-of-thought: An explicit multi-step reasoning trace produced by a model to reach an answer. "implicit in-weights reasoning, i.e., reasoning over knowledge from the weights without emitting an explicit chain of thought."
- Clever Hans cheat: A shortcut strategy learned by a model that fits outputs using superficial patterns instead of true reasoning. "the model learns a trivial solution (termed a Clever Hans cheat) that is much simpler than planning"
- decoder-only Transformer: A Transformer architecture that uses only the decoding stack for autoregressive next-token prediction. "We use a from-scratch, decoder-only Transformer (GPT-mid)"
- dual-encoder models: Retrieval architectures that encode queries and documents independently into a shared embedding space for similarity search. "and traditional dual-encoder models"
- embedding bottleneck: A capacity constraint where limited embedding dimensionality restricts what information can be represented. "especially the embedding bottleneck"
- Fiedler vector(s): The eigenvectors associated with the smallest non-zero eigenvalues of a graph Laplacian, capturing coarse global structure. "called the Fiedler vector(s)"
- generative retrieval models: Approaches that formulate information retrieval as sequence generation with LLMs. "modern generative retrieval models"
- geometric view of memory: A perspective where parametric memory is encoded in the geometry of embeddings, capturing global relationships. "implying a geometric view of memory."
- implicit in-weights reasoning: Reasoning that relies on knowledge stored in the model’s parameters without producing an explicit rationale. "implicit in-weights reasoning, i.e., reasoning over knowledge from the weights without emitting an explicit chain of thought."
- Mamba: A sequence modeling architecture based on selective state spaces, proposed as an alternative to Transformers. "both the Transformer and Mamba"
- negative graph Laplacian: The negated Laplacian operator of a graph; its top eigenvectors reveal global structural patterns. "top (non-degenerate) eigenvectors of the negative graph Laplacian."
- Node2Vec: A node embedding method that learns representations via biased random walks on graphs. "connection to Node2Vec"
- parametric memory: The information stored in a model’s weights that encodes facts or associations learned during training. "the parametric memory of atomic facts"
- path-star graph: A tree where a single root branches into multiple disjoint paths of uniform length. "path-finding on path-star graphs"
- path-star topology: The structural layout of a path-star graph, emphasizing its branching and path lengths. "The path-star topology"
- Platonic representation hypothesis: The idea that different models converge to similar internal representations, reflecting an underlying ideal form. "the Platonic representation hypothesis"
- pre-caching gradients: Gradient signals from future tokens that influence earlier positions during training. "pre-caching gradients"
- reversal curse: A phenomenon where models trained on one directional association struggle to generalize to the reversed association. "in order to dodge the reversal curse"
- spectral bias: A tendency of learning dynamics to favor low-frequency (smooth) components aligned with leading eigenvectors of an operator. "stems from a spectral bias"
- spectral norms: Operator norms corresponding to the largest singular value; used to assess complexity or stability of learned representations. "e.g., flatness or spectral norms"
- superposition: The linear combination of features within shared neurons or dimensions, enabling compact representation of multiple concepts. "linear representations and superposition in interpretability"
- teacherless training: A setup where the model is trained without teacher forcing, exposing it to its own predictions during sequence learning. "(under teacherless training)"
Collections
Sign up for free to add this paper to one or more collections.