Quantum Combinatorial Reasoning for Large Language Models (2510.24509v1)

Abstract: We design and implement a quantum combinatorial reasoning framework for LLMs (QCR-LLM), integrating a real quantum computer in the hybrid workflow. QCR-LLM reformulates reasoning aggregation as a higher-order unconstrained binary optimization (HUBO) problem. In this sense, reasoning fragments are represented as binary variables and their interactions encode statistical relevance, logical coherence, and semantic redundancy. We tackle the resulting high-order optimization problem both classically, via simulated annealing, and quantumly through the bias-field digitized counterdiabatic quantum optimizer (BF-DCQO) executed on IBM's superconducting digital quantum processors. Experiments on BIG-Bench Extra Hard (BBEH) benchmarks demonstrate that our QCR-LLM consistently improves reasoning accuracy across multiple LLM backbones, surpassing reasoning-native systems such as o3-high and DeepSeek R1 by up to $+9\,$pp. Despite requiring multiple reasoning samples per query, our QCR-LLM remains approximately five times more energy-efficient than o3-high, owing to the low per-token energy footprint of its GPT-4o backbone. These results constitute the first experimental evidence of quantum-assisted reasoning, showing that hybrid quantum-classical optimization can efficiently enhance reasoning coherence, interpretability, and sustainability in large-scale LLMs. We have opened the doors to the emergence of quantum intelligence, where harder prompts require quantum optimizers at quantum-advantage level.

• The paper presents a novel quantum-assisted framework that reformulates multi-sample LLM reasoning as a Higher-Order Unconstrained Binary Optimization problem to capture complex semantic dependencies.
• It integrates classical simulated annealing with BF-DCQO quantum optimization to select stable reasoning fragments, achieving significant improvements in reasoning accuracy.
• The experimental results demonstrate enhanced logical coherence and energy efficiency, paving the way for scalable, quantum-enhanced AI reasoning systems.

Quantum Combinatorial Reasoning for LLMs: A Technical Analysis

Introduction and Motivation

The paper presents Quantum Combinatorial Reasoning for LLMs (QCR-LLM), a hybrid framework that integrates LLM-based reasoning with high-order combinatorial optimization, leveraging both classical and quantum solvers. The central innovation is the reformulation of reasoning aggregation as a Higher-Order Unconstrained Binary Optimization (HUBO) problem, enabling explicit modeling of multi-fragment dependencies, logical coherence, and semantic redundancy. This approach addresses the limitations of prior aggregation methods—such as Chain-of-Thought (CoT), Self-Consistency, and Tree-of-Thoughts—which rely on heuristic voting or traversal and fail to capture higher-order semantic interactions.

Pipeline: From Multi-Sample CoT to HUBO

The QCR-LLM pipeline begins with multi-sample zero-shot CoT prompting, generating $N$ independent reasoning traces per query. Each trace is parsed into atomic reasoning fragments, which are semantically normalized and deduplicated using sentence embeddings and cosine similarity thresholds. The resulting pool of $R$ distinct fragments forms the basis for combinatorial selection.

Each fragment $r_i$ is assigned a binary variable $x_i \in \{0,1\}$, indicating its inclusion in the final reasoning chain. The aggregation is formalized as a HUBO problem:

$$H(\mathbf{x}) = \sum_{\emptyset\neq S\subseteq [R],\ |S|\le K} w_S \prod_{i\in S} x_i$$

where $w_S$ encodes statistical relevance, logical coherence, and semantic redundancy for each subset $S$ of fragments. Coefficient design incorporates empirical popularity, stability, pairwise and higher-order co-occurrence, and semantic similarity penalties, ensuring that the optimization landscape favors coherent and diverse reasoning chains.

Optimization: Classical and Quantum Solvers

For $K \leq 3$, classical simulated annealing (SA) is employed, with cubic terms reduced to quadratic form via redistribution of interactions. However, this reduction introduces approximation bias and inflates the number of variables, limiting scalability. For higher-order or dense HUBOs, the Bias-field Digitized Counterdiabatic Quantum Optimizer (BF-DCQO) is used, executed on IBM superconducting quantum hardware. BF-DCQO natively handles $k$-body interactions, leveraging engineered bias fields and counterdiabatic schedules to efficiently traverse the energy landscape and recover near-optimal solutions.

The optimization process yields a distribution over low-energy configurations, from which the expected inclusion frequency of each fragment is computed. Stable fragments—those appearing consistently in the lowest-energy solutions—are selected to form the backbone of the aggregated reasoning chain.

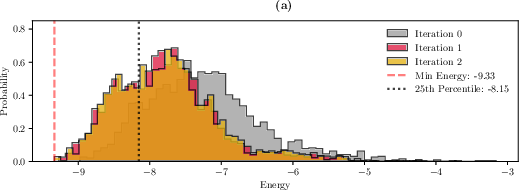
Figure 1: BF-DCQO optimization process for a Causal Understanding question, showing energy landscape convergence and inclusion frequency ranking for reasoning fragments.

End-to-End QCR-LLM Workflow

The complete QCR-LLM workflow integrates multi-sample CoT generation, semantic aggregation, HUBO construction, solver execution (classical or quantum), and final synthesis. The selected stable reasoning fragments are reintroduced into the LLM as contextual evidence, guiding the model to produce the final answer. This process transforms stochastic LLM reasoning into a controlled, interpretable, and physically grounded optimization problem.

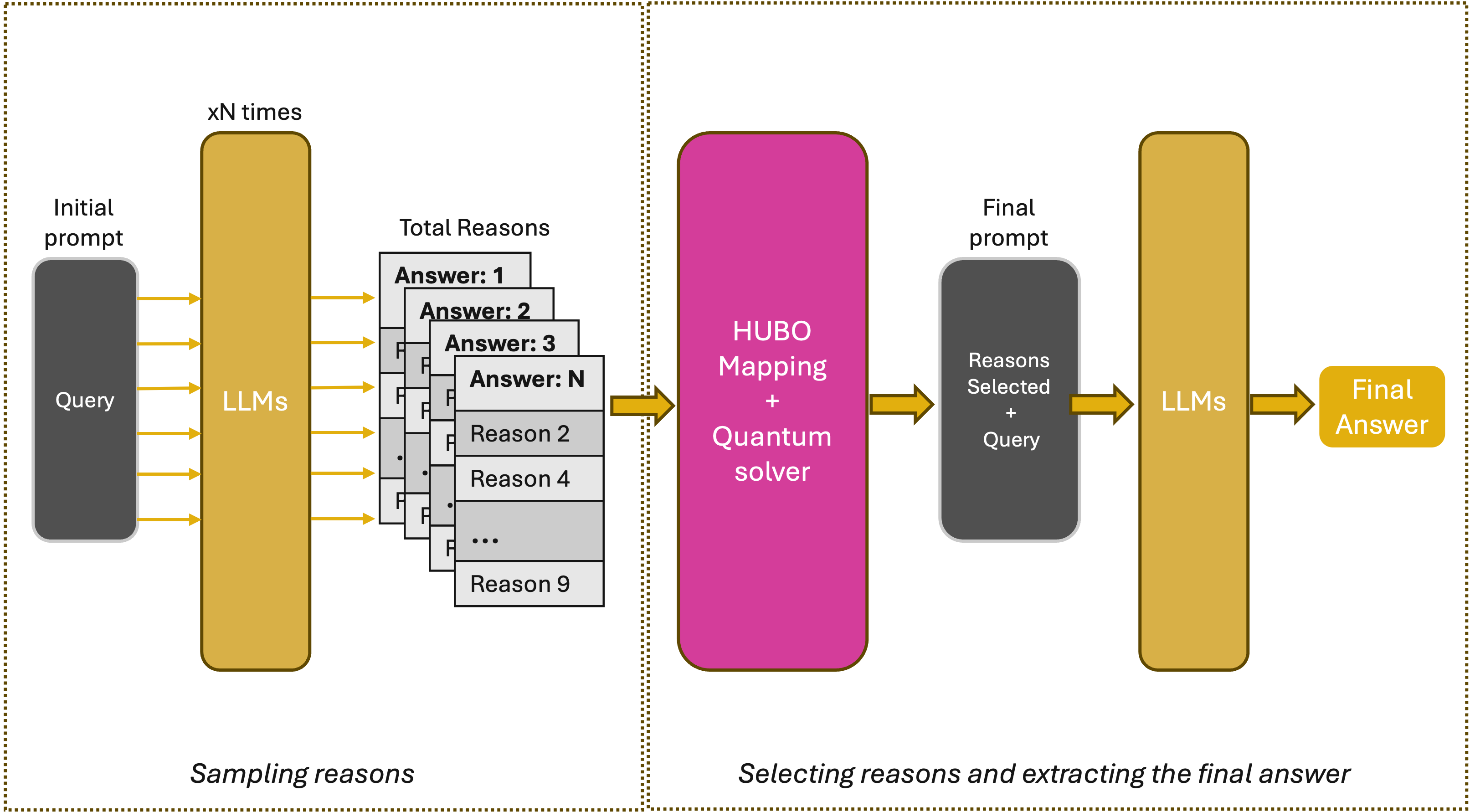
Figure 2: QCR-LLM pipeline overview, illustrating the flow from multi-sample CoT to quantum-optimized reasoning selection and final answer generation.

Experimental Results: BIG-Bench Extra Hard

QCR-LLM was evaluated on three BBEH subsets: Causal Understanding, DisambiguationQA, and NYCC. The framework consistently improved reasoning accuracy across all tested LLM backbones, including GPT-4o, DeepSeek V1, and LLaMA 3.1. Notably, QCR-LLM (GPT-4o) achieved up to +8.3 pp improvement over the base model and outperformed reasoning-native systems such as o3-high and DeepSeek R1 by up to +9 pp.

Quantum optimization via BF-DCQO yielded further gains over classical SA, with direct handling of higher-order interactions and preservation of the original reasoning Hamiltonian. The quantum solver demonstrated modest but positive improvements, with the potential for greater advantage as reasoning complexity and problem size increase.

Energy Efficiency

QCR-LLM maintains favorable energy efficiency despite requiring multiple reasoning samples per query. Under realistic inference workloads (NVIDIA H100, 500 tokens/query), GPT-4o exhibits a per-token energy cost two orders of magnitude lower than o3-high. Even with 20 completions per query, QCR-LLM (GPT-4o) remains approximately five times more energy-efficient than o3-high, highlighting the sustainability of the approach.

Theoretical and Practical Implications

QCR-LLM establishes reasoning aggregation as a structured optimization problem, decoupled from the linguistic domain and compatible with both classical and quantum solvers. The framework is model-agnostic, requiring no retraining or architectural modification, and can be extended to multi-model or hybrid configurations. The explicit modeling of higher-order dependencies enables coherent, interpretable reasoning chains, with quantum solvers providing computational advantage in regimes where classical heuristics fail.

The empirical results demonstrate that quantum-assisted reasoning can enhance both accuracy and interpretability in LLMs, with energy efficiency suitable for large-scale deployment. The approach lays the groundwork for future exploration of quantum advantage in AI reasoning, particularly for tasks with combinatorial complexity beyond the reach of classical solvers.

Future Directions

Potential extensions include:

• Scaling to higher-order ($K > 3$) interactions, where quantum solvers can demonstrate clear computational advantage.
• Sequential and hierarchical reasoning pipelines, enabling multi-stage optimization and reasoning refinement.
• Hybrid aggregation of reasoning samples from diverse LLMs, leveraging complementary strengths within a unified quantum-optimized framework.
• System-level energy accounting, including quantum backend overheads, for comprehensive sustainability analysis.

Conclusion

QCR-LLM represents a rigorous integration of LLM reasoning with combinatorial optimization, leveraging quantum algorithms to enhance coherence, interpretability, and efficiency. The framework demonstrates consistent empirical improvements over state-of-the-art baselines and establishes a paradigm for quantum-enhanced reasoning in large-scale AI systems. As quantum hardware matures, the approach is poised to unlock new regimes of reasoning complexity and computational efficiency, advancing the frontier of hybrid quantum–classical intelligence.