Hybrid Sequential Quantum Computing (2510.05851v1)

Abstract: We introduce hybrid sequential quantum computing (HSQC), a paradigm for combinatorial optimization that systematically integrates classical and quantum methods within a structured, stage-wise workflow. HSQC may involve an arbitrary sequence of classical and quantum processes, as long as the global result outperforms the standalone components. Our testbed begins with classical optimizers to explore the solution landscape, followed by quantum optimization to refine candidate solutions, and concludes with classical solvers to recover nearby or exact-optimal states. We demonstrate two instantiations: (i) a pipeline combining simulated annealing (SA), bias-field digitized counterdiabatic quantum optimization (BF-DCQO), and memetic tabu search (MTS); and (ii) a variant combining SA, BF-DCQO, and a second round of SA. This workflow design is motivated by the complementary strengths of each component. Classical heuristics efficiently find low-energy configurations, but often get trapped in local minima. BF-DCQO exploits quantum resources to tunnel through these barriers and improve solution quality. Due to decoherence and approximations, BF-DCQO may not always yield optimal results. Thus, the best quantum-enhanced state is used to continue with a final classical refinement stage. Applied to challenging higher-order unconstrained binary optimization (HUBO) problems on a 156-qubit heavy-hexagonal superconducting quantum processor, we show that HSQC consistently recovers ground-state solutions in just a few seconds. Compared to standalone classical solvers, HSQC achieves a speedup of up to 700 times over SA and up to 9 times over MTS in estimated runtimes. These results demonstrate that HSQC provides a flexible and scalable framework capable of delivering up to two orders of magnitude improvement at runtime quantum-advantage level on advanced commercial quantum processors.

• The paper presents HSQC, which integrates simulated annealing, BF-DCQO, and memetic tabu search to tackle higher-order binary optimization problems.
• Key results include up to a 700x speedup over simulated annealing and improved solution quality compared to conventional methods like CPLEX.
• Experimental validation on IBM's superconducting quantum processor demonstrates HSQC's scalability and practical potential in real-world optimization challenges.

Hybrid Sequential Quantum Computing: A Framework for Optimization

Introduction

The paper introduces Hybrid Sequential Quantum Computing (HSQC), an optimization framework that leverages both classical and quantum resources to solve combinatorial optimization problems more efficiently than standalone methods. HSQC orchestrates a sequential pipeline combining Simulated Annealing (SA), Bias-Field Digitized Counterdiabatic Quantum Optimization (BF-DCQO), and Memetic Tabu Search (MTS), with experimental validation on IBM's superconducting quantum processors, showcasing significant speedups over conventional solvers.

Framework Overview

HSQC is designed to optimize higher-order unconstrained binary optimization (HUBO) problems by exploiting the complementary strengths of classical and quantum computing methods. Classical solvers effectively explore large-scale problem landscapes but often struggle with local minima. Conversely, quantum components like BF-DCQO leverage quantum superposition and tunneling to escape these minima and refine solutions further.

Figure 1: Schematic of the hybrid sequential quantum computing (HSQC) framework.

The framework begins with classical solvers like SA to identify good starting points in the search space, thereafter leveraging BF-DCQO for quantum refinement, followed by a final classical stage such as MTS or a second round of SA for precise solution refinements.

Higher-order Binary Optimization and Implementation Details

HUBO problems extend QUBO by considering interactions among multiple binary variables, crucial for modeling complex interactions in various applications. HSQC's implementation on IBM's 156-qubit superconducting quantum processor utilizes SA to produce initial configurations, which are then optimized by BF-DCQO. The quantum stage executes digitized counterdiabatic evolution, adaptive to problem characteristics, to identify superior configurations (Figure 2).

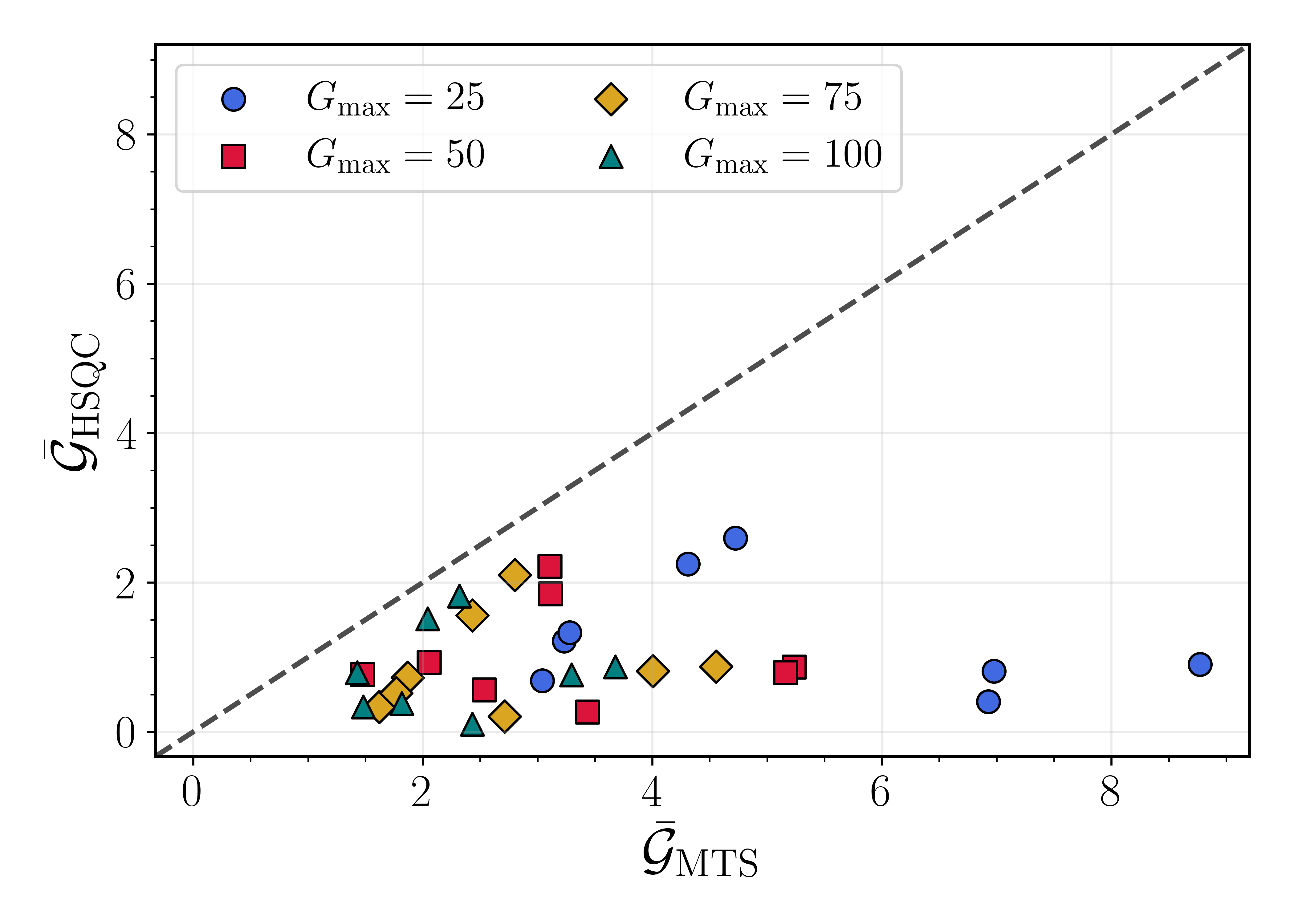
Figure 2: Performance comparison between MTS and HSQC.

The quantum state evolves using a first-order nested commutator approximation to efficiently traverse the landscape, initialized with optimal bias fields derived from classical outputs. A combination of SA and BF-DCQO initializes MTS, which combines evolutionary algorithms with tabu search for local exploitation, enhancing classical search effectiveness by using quantum-discovered bitstrings.

Results and Performance Analysis

The paper reports significant improvements with HSQC in solving benchmark HUBO instances over solely classical methods. By assessing minimum energy values and optimality gaps, HSQC consistently outperformed classical solvers, achieving up to a 700x speedup over SA and 9x over MTS in runtime estimates. Notably, HSQC could solve instances close to or better than CPLEX's exact solutions with fewer resources (Figure 3).

Figure 3: Minimum tau values for various standalone optimization routines for Instance 8.

In practice, HSQC offers a substantial reduction in convergence times and enhanced probability of identifying ground state solutions. The orchestration of solver stages within HSQC facilitates a holistic, adaptive optimization approach, balancing exploratory capabilities with precision refinement efficiencies.

Discussion and Future Applications

HSQC presents a scalable and adaptable framework suitable for current quantum hardware limitations, offering practical runtime quantum advantages in optimization tasks. As quantum technologies mature, further developments could enhance HSQC's application breadth to two-dimensional architectures with higher connectivity, potentially broadening the class of solvable problems and amplifying quantum advantages.

These advancements propose a pathway for industry-adapted hybrid models, integrating intelligent AI capabilities. The approach may redefine solution methodologies in quantum machine learning, material simulations, and beyond, illustrating a viable trajectory for hybrid-optimized quantum solutions aligned with real-world demands.

Conclusion

The HSQC paradigm demonstrates a compelling intersection of classical robustness and quantum potentials, marking a pivotal step in hybrid computational problem-solving. By blending classical initializations with quantum refinements and final projections, HSQC establishes a leading framework for addressing complex optimization challenges, facilitating future expansions alongside evolving quantum technologies.