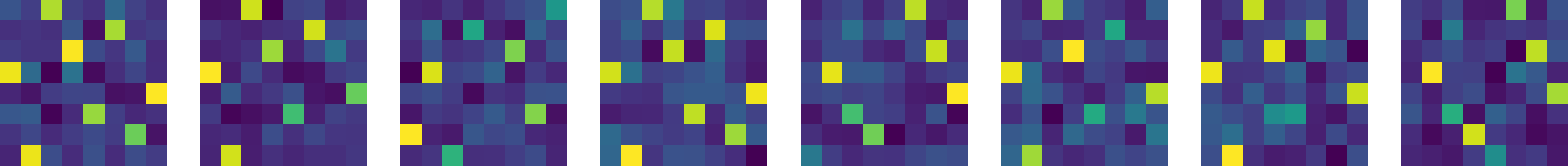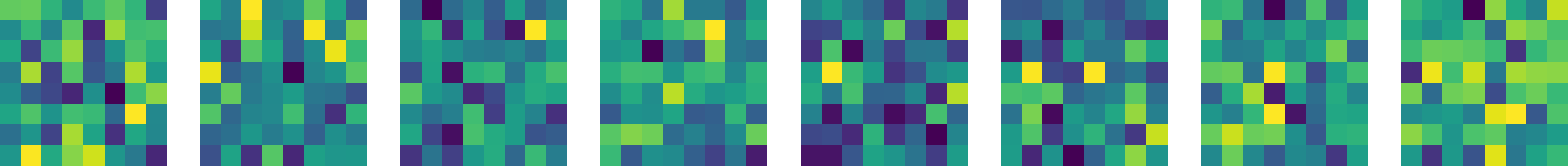Generalizable Reasoning through Compositional Energy Minimization (2510.20607v1)

Abstract: Generalization is a key challenge in machine learning, specifically in reasoning tasks, where models are expected to solve problems more complex than those encountered during training. Existing approaches typically train reasoning models in an end-to-end fashion, directly mapping input instances to solutions. While this allows models to learn useful heuristics from data, it often results in limited generalization beyond the training distribution. In this work, we propose a novel approach to reasoning generalization by learning energy landscapes over the solution spaces of smaller, more tractable subproblems. At test time, we construct a global energy landscape for a given problem by combining the energy functions of multiple subproblems. This compositional approach enables the incorporation of additional constraints during inference, allowing the construction of energy landscapes for problems of increasing difficulty. To improve the sample quality from this newly constructed energy landscape, we introduce Parallel Energy Minimization (PEM). We evaluate our approach on a wide set of reasoning problems. Our method outperforms existing state-of-the-art methods, demonstrating its ability to generalize to larger and more complex problems. Project website can be found at: https://alexoarga.github.io/compositional_reasoning/

• The paper introduces a novel compositional energy minimization framework that reformulates reasoning tasks as optimization problems.
• It proposes Parallel Energy Minimization (PEM) which uses particle sampling and resampling to navigate complex energy landscapes and avoid local minima.
• Experimental results on N-Queens, 3-SAT, and graph coloring demonstrate significant improvements in scalability and solution quality.

Generalizable Reasoning through Compositional Energy Minimization

Introduction

The paper "Generalizable Reasoning through Compositional Energy Minimization" introduces a novel approach to enhance the generalization capabilities of models tasked with reasoning beyond their training distributions. Traditional methods train models in an end-to-end manner, which limits their ability to tackle more complex, out-of-sample reasoning problems. In contrast, this paper proposes an optimization-based framework that constructs energy landscapes from simpler subproblems, facilitating better generalization by combining these energy landscapes to solve larger and more intricate problems.

Methodology

Compositional Energy Landscapes

The core idea is to represent reasoning tasks as optimization problems defined over energy landscapes. The energy function $E_{\theta}(\bm{x}, \bm{y})$ assigns lower energy to valid solutions $\bm{y}$ given the inputs $\bm{x}$. Reasoning is thus an optimization task where the objective is to find $\bm{y}$ that minimizes the energy function:

$$\hat{\bm{y}} = \arg\min_{\bm{y}} E_{\theta}(\bm{x}, \bm{y})$$

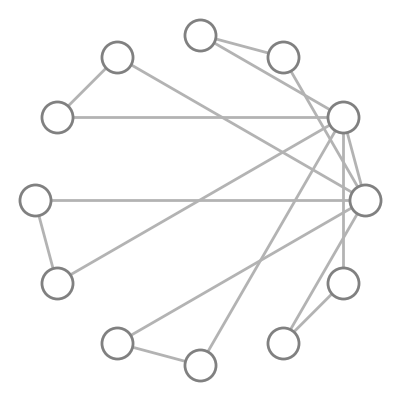
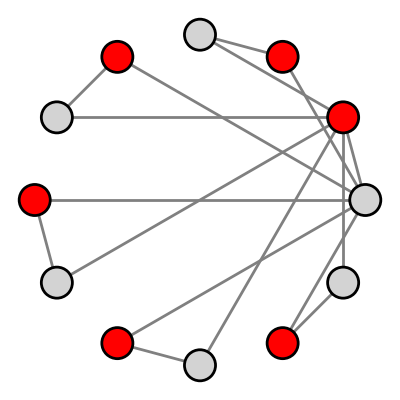
Figure 1: Compositional Generalizable Reasoning. We formulate reasoning as an optimization problem with inputs $\bm{x}$ and solutions $\bm{y}$. By combining multiple optimization objectives, we can generalize to larger problem instances.

Parallel Energy Minimization (PEM)

To efficiently explore complex energy landscapes, the paper introduces Parallel Energy Minimization (PEM), a sampling strategy that leverages parallel particles to avoid local minima. PEM uses resampling based on energy levels, enhancing both exploration and convergence to valid solutions:

Algorithm: Parallel Energy Minimization (PEM) 1. Initialize particles with Gaussian noise. 2. For each timestep t, calculate particle weights based on energy. 3. Resample particles using softmax of negative energy. 4. Add Gaussian noise for exploration. 5. Update particles by calculating the energy gradient.

This approach reduces the likelihood of particles getting trapped in non-optimal regions, improving the quality of generated solutions.

Experiments

N-Queens Problem

The authors demonstrated the efficacy of their method on the N-Queens problem by achieving superior results compared to existing combinatorial optimization models. The approach uses a composition of energy functions derived from solving smaller subproblems, enabling it to scale competently to larger board sizes:

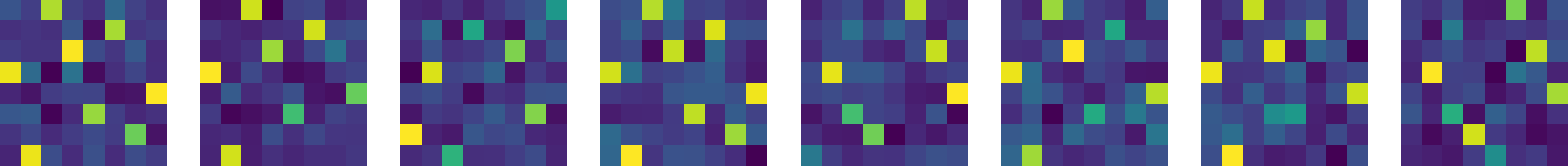
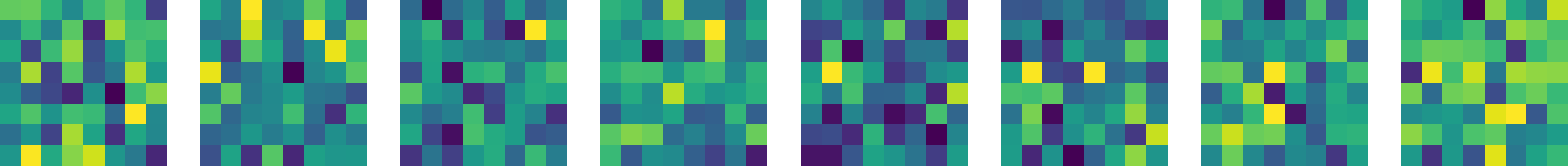
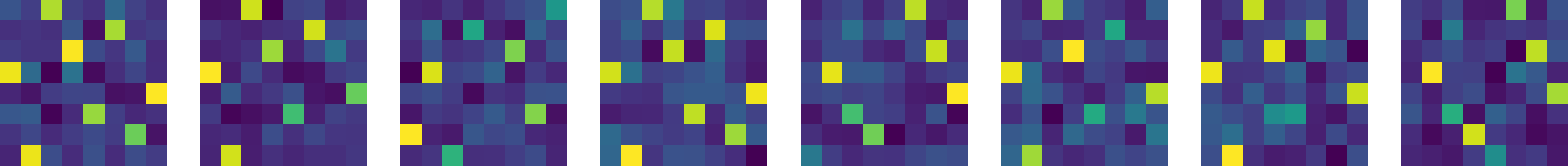
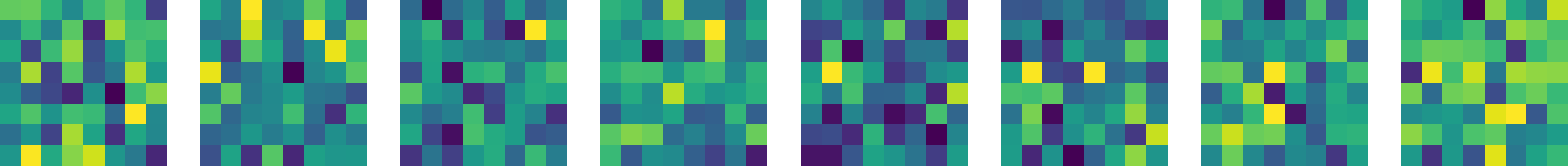
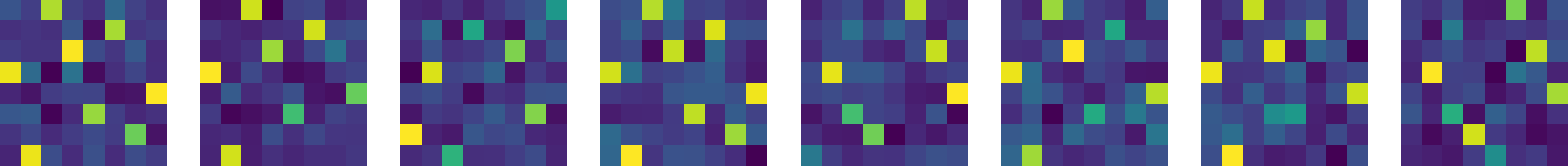
Figure 2: Optimized Samples Across Timesteps. Generated samples where yellow squares represent queens placed in the chessboard. Reverse diffusion fails to find valid solutions (top). Increasing the number of particles with PEM leads from invalid solutions (middle) to valid solutions (bottom).

3-SAT and Graph Coloring

In addition to N-Queens, the method was tested on 3-SAT and graph coloring problems. The compositional strategy, paired with PEM, outperformed state-of-the-art models by solving a higher proportion of problem instances and handling larger datasets successfully.

Figure 3: Energy Maps for Valid and Invalid Solutions in 3-SAT. Higher energy is assigned to unsatisfied clauses, aiding the optimization process in achieving valid assignments.

Implications

Practical Implications

The proposed method demonstrates substantial improvements in generalization for reasoning tasks and is particularly useful in domains requiring robust decision-making under novel constraints, such as symbolic AI, logic puzzles, and optimization problems in logistics and scheduling.

Theoretical Implications

The use of compositional energy minimization frameworks opens new avenues for research in reasoning across complex domains. The integration of simple subproblem solutions into a cohesive model challenges existing paradigms about the scalability of reasoning and optimization in AI.

Conclusion

The approach outlined in this paper represents a significant advancement in reasoning using AI. By harnessing energy-based models and compositional techniques, it achieves superior generalization and solution quality across various reasoning tasks. Future research could explore broader applications and adaptations to non-Gaussian energy landscapes, further enhancing the method's robustness and applicability to diverse problem domains.