Trapped-ion two-qubit gates with >99.99% fidelity without ground-state cooling (2510.17286v1)
Abstract: We introduce the 'smooth gate', an entangling method for trapped-ion qubits where residual spin-motion entanglement errors are adiabatically eliminated by ramping the gate detuning. We demonstrate electronically controlled two-qubit gates with an estimated error of $8.4(7)\times10{-5}$ without ground-state cooling. We further show that the error remains $\lesssim 5\times10{-4}$ for ions with average phonon occupation up to $\bar{n}=9.4(3)$ on the gate mode. These results indicate that trapped-ion quantum computation can achieve high fidelity at temperatures above the Doppler limit, which enables faster and simpler device operation.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What this paper is about
This paper shows a new way to make two ions (tiny charged atoms) share quantum information very accurately, without first chilling their motion to the absolute minimum. The team achieves two‑qubit gate errors as low as about 1 in 10,000 (and sometimes even better), while the ions are still “warm” by quantum standards. This could make trapped‑ion quantum computers faster and simpler to run.
The main questions the researchers asked
- Can we perform extremely accurate two‑qubit gates in trapped ions without doing slow, complicated extra cooling (called ground‑state cooling)?
- Can we design these gates so they are naturally robust to small drifts and noise in the ions’ motion?
- Can this be done with simple controls that are easy to calibrate?
How the method works (in simple terms)
Think of each ion as a tiny ball on a spring that can vibrate. Each ion also has a “spin” (its qubit), which you can think of as a tiny arrow pointing up or down. To entangle two ions (make their qubits share information), you apply a force that depends on their spins, nudging the balls on springs in a coordinated way.
Two key ideas:
- Detuning: This is like pushing a swing slightly off its natural rhythm. The amount you are “off‑beat” is the detuning.
- Adiabatic vs. diabatic:
- Diabatic (fast) changes are like suddenly yanking the swing—you must stop at exactly the right instant or it keeps wobbling.
- Adiabatic (smooth) changes are like slowly moving the swing’s resting point so the seat calmly follows with little leftover wobble.
In most older methods, the force is turned on and off quickly and must be timed perfectly to avoid leaving extra motion tied to the spin (called “spin‑motion entanglement,” which causes errors, especially if the ions aren’t very cold).
The new “smooth gate” does the opposite:
- Keep the push strength steady.
- Smoothly change the detuning (how off‑beat you are) during the gate.
- Because the change is smooth and slow compared to the motion, the ions’ motion follows along gently and ends up back where it started—so there’s almost no leftover wobble connected to the spin.
A few more practical ingredients:
- They use electronic (microwave) signals near the ions, not lasers, to create the spin‑dependent force. Electronics are very stable, create almost no unwanted light effects, and make it easy to change the frequency smoothly.
- Calibration is simple: you mostly just choose the lowest detuning value to set the gate strength (the entangling angle). It’s basically one main knob to turn.
What they did in the lab
- They used two calcium ions as qubits.
- Instead of cooling the motion all the way to the “ground state,” they left the ions at or above the normal laser‑cooling limit (the Doppler limit), which is much easier and faster to reach.
- They ran many sequences of their smooth two‑qubit gates and measured how often the results matched what a perfect gate would do.
- They also checked how sensitive the gate was to small errors, like if the ions’ natural vibration frequency drifted a little.
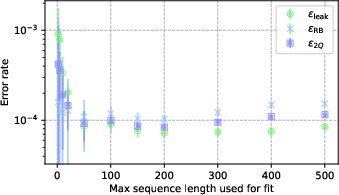
To test gate quality, they used a version of randomized benchmarking tailored to detect when the system leaks out of the intended two‑state subspace (so they can tell apart simple phase errors from motion‑related “leakage” errors). You can think of this like giving the gate a long, mixed workout and seeing how much performance drops off—separating different kinds of mistakes.
The main results and why they matter
- Very high accuracy without extra cooling:
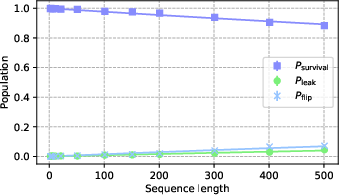
- Estimated error per two‑qubit gate as low as about 8.4 × 10⁻⁵ (that’s better than 99.9916% success) in sequences up to a few hundred gates.
- Even over longer sequences, the average error stayed around 1.16 × 10⁻⁴.
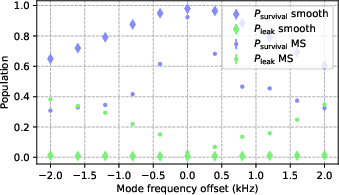
- Works well even when ions are “warm”:
- The error stayed below about 5 × 10⁻⁴ even when the ions had a lot of motion (well above the Doppler limit).
- Robust to drifts:
- The smooth gate is much less sensitive to small, static errors in the ions’ vibration frequency than standard methods. In simple words: even if the “spring” frequency shifts a bit, the gate still works well.
- Simple calibration:
- Mostly one main parameter (the minimum detuning) sets the entangling strength, making setup and maintenance easier.
Why this is important:
- Not needing ground‑state cooling removes a big time and engineering burden. Cooling to the ground state can take much longer than running the gates themselves.
- Robustness to noise and simple calibration are crucial for scaling up to many qubits.
- These error rates are in the range needed for error‑corrected quantum computing and for running very long circuits in near‑term devices.
What this could change in the future
- Faster quantum computers: Skipping ground‑state cooling can save a lot of time per operation and simplify hardware (fewer lasers, less optical complexity).
- Easier scaling: Smooth, electronic control and simple calibration make it more practical to run many gate zones at once and manage large devices.
- Better algorithms today, fault‑tolerance tomorrow: With errors around 10⁻⁴, you can run many thousands of gates reliably, and you’re approaching the levels needed for efficient quantum error correction with low overhead.
In short, the “smooth gate” approach shows that trapped‑ion quantum computers can be both highly accurate and much simpler to operate, even without ultra‑cold motion—an important step toward practical, large‑scale quantum machines.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
The following list summarizes what remains missing, uncertain, or unexplored in the paper, framed so future researchers can act on it:
- Optimal ramp design: The detuning ramp was chosen heuristically (parameter j=3); there is no formal optimization of δ(t) (or joint optimization of Ωg(t), δ(t)) against a rigorously defined objective (e.g., minimizing residual spin–motion entanglement subject to gate-time and hardware constraints). Derive and test optimal control solutions (e.g., variational methods, convex formulations, GRAPE/CRAB) and compare fidelities and durations.
- Adiabaticity-to-error bounds: The adiabaticity condition (ẋβ/δ ≪ 1) is stated qualitatively without quantitative bounds linking ramp parameters to residual spin–motion entanglement and gate infidelity. Develop analytic bounds and closed-form scaling laws that translate ramp smoothness, δmin/δmax, and τd, τg into predicted error floors.
- Full error budget: The paper does not provide a comprehensive error decomposition (e.g., dephasing, geometric-phase miscalibration, residual entanglement, amplitude/phase noise, AC Zeeman/Stark shifts, technical waveform errors). Perform a systematic error-budget paper using interleaved benchmarking, parametric scans, and independent calibrations to quantify each contribution.
- Benchmarking beyond SU(2) subspace: Reported fidelities are “subspace benchmarked.” Validate gate fidelity on the full two-qubit Hilbert space (e.g., two-qubit Clifford RB, cycle benchmarking, randomized compiling, GST) and cross-check with Bell-state tomography to rule out subspace-specific biases.
- SPAM assumptions: SLERB analysis assumes negligible SPAM and relies on Pauli randomization to mitigate asymmetries. Explicitly quantify SPAM errors and confirm they do not bias inferred gate error at the 10⁻⁴ level; include SPAM-robust fitting or SPAM calibration.
- Non-Markovianity characterization: A ~3×10⁻⁵ increase in inferred error for longer sequences is attributed to qubit frequency drift without direct evidence. Measure the magnetic-field noise spectrum and timescales, quantify its impact on gate error, and test mitigation (e.g., active field stabilization, improved dynamical decoupling within the gate).
- Carrier decoupling optimization: The carrier π-phase flip at mid-gate is ad hoc. Optimize carrier sequences (timing, phase, amplitude) analytically/numerically to minimize interplay with entangling dynamics and residual errors; compare alternative DD sequences (Uhrig, CPMG, toggling-frame designs).
- Gate-induced heating: The paper does not quantify per-gate heating of the motional mode(s). Directly measure changes in phonon occupation before/after gates across temperatures to determine if the smooth gate injects energy into motion.
- Robustness to realistic noise spectra: Filter functions were computed against single-tone detuning fluctuations. Measure the actual motional-frequency noise PSD in the device, integrate the filter function against that PSD, and validate predictions experimentally.
- Amplitude/phase noise sensitivity: The filter-function analysis focuses on detuning errors. Derive and measure sensitivity to microwave amplitude and phase noise (including AWG/DAC quantization and frequency-slew nonidealities), and design control strategies or ramp shapes to minimize these errors.
- Multi-mode effects and avoided crossings: Detuning sweeps may transiently reduce detuning to spectator modes or cross near other motional resonances, potentially increasing off-mode coupling. Map the full mode spectrum, analyze transient couplings during δ(t), and set constraints on δmin/δmax and τd to avoid unintended interactions.
- Scaling to larger ion crystals: Demonstrations are on two ions. Evaluate AESE and fidelity in multi-ion chains (with closely spaced modes and stronger mode crowding), including gates targeted to specific pairs, cross-talk to spectators, and performance with multiple concurrent gate operations.
- Parallel gates with global drives: The architecture discussion proposes simultaneous gates across zones with local DC shims. Experimentally demonstrate parallel smooth gates, quantify zone-to-zone crosstalk, robustness to DC-shim drift, and overhead for per-zone calibration and re-shimming.
- Transport-integrated performance above Doppler: While the gate tolerates high n̄, the work does not demonstrate long circuits with frequent transports (split/merge, junctions) and no mid-circuit ground-state cooling. Execute end-to-end circuits with transport-induced heating and quantify gate fidelity, speedups, and thermal robustness.
- Upper temperature limits and non-thermal states: Fidelity is shown up to n̄≈9.4 in the gate mode with near-thermal distributions. Determine performance at significantly higher n̄, with non-thermal distributions (e.g., coherent displacements from transport), and with occupation across multiple spectator modes.
- Gate-speed vs fidelity trade-offs: Gate duration (~226 μs) is longer than typical diabatic MS gates. Map the fidelity-time frontier by varying δmin, τd, τg, Ωg to identify practical operating points for QEC cycle times; explore shortcuts to adiabaticity (counterdiabatic driving, LR invariants) to reduce duration while preserving AESE.
- Ramp implementation limits: Frequency slewing and amplitude ramps depend on AWG/DDS resolution, latency, and linearity. Quantify sensitivity to finite update rates, phase continuity, and discretization, and set hardware requirements to sustain 10⁻⁴-level fidelity.
- AC Zeeman/Stark shifts during ramps: With bichromatic tones near sidebands, time-dependent AC shifts may arise as δ(t) changes. Measure and model these shifts across the ramp, and apply compensation (e.g., phase/ frequency modulation or additional tones).
- Species and qubit-type generality: Demonstration uses magnetic-field-sensitive Zeeman qubits in ⁴⁰Ca⁺. Test with hyperfine or clock qubits (e.g., ⁹Be⁺, ¹⁷¹Yb⁺) to assess improvements in dephasing-limited errors and possible changes in control constraints.
- Micromotion and trap non-idealities: The analysis assumes ideal harmonic motion. Characterize sensitivity to excess micromotion, anharmonicity, and stray fields, and verify AESE under realistic trap imperfections.
- Application to other gate types: The smooth-gate concept is claimed to apply broadly (e.g., ZZ gates). Demonstrate smooth ZZ gates and compare robustness and speed to smooth MS gates.
- Detuning calibration range and automation: Calibration relies on scanning δmin to identify θg≈π/2 under AESE. Develop automated, drift-resilient calibration protocols, quantify calibration time/cost, and demonstrate stability over days and across zones.
- Crosstalk and addressing with global drives: Quantitatively assess how local DC frequency offsets suppress undesired interactions, the residual coupling between non-target pairs, and the fidelity impact of imperfect addressing.
- Constraints from mode spacing: Provide concrete design rules linking required δmax, δmin, and τd to the trap’s mode spacing and gradients, ensuring AESE without interacting with neighboring modes in scalable devices.
- Hybrid robust-control strategies: Compare smooth detuning ramps with amplitude-shaped MS pulses, composite sequences, and Walsh variants; explore hybrid approaches that combine the best features for given hardware and noise.
- Real-time detuning feedback: Investigate on-the-fly correction of δ(t) using motional-frequency tracking to suppress slow drifts and maintain AESE across long circuits.
- Validation of “record-high” claim: Establish standardized cross-platform benchmarks and community-agreed metrics (full-Clifford RB, cycle benchmarking) to confirm comparability of “>99.99%” claims across modalities.
- Documentation for reproducibility: Provide complete gate parameter sets, waveform definitions, and calibration procedures (including δ(t), Ωg(t), phases, carrier timing) to enable replication and meta-analyses across different setups.
Practical Applications
Immediate Applications
Below are actionable uses that can be deployed now (or with modest engineering), derived directly from the paper’s findings and methods.
- High‑fidelity two‑qubit gates without ground‑state cooling
- Sectors: Quantum hardware, cloud services, academia
- Use case: Replace diabatic MS gates with the “smooth gate” (adiabatic detuning ramp) to achieve ~1e-4 error rates at or above the Doppler limit, reducing calibration complexity and thermal sensitivity.
- Tools/products/workflows:
- Firmware/FPGA updates to AWGs/DDS synthesizers to generate phase‑coherent, ramped detuning profiles with smooth boundary conditions (Eq. (det_ramp_func), j≈3).
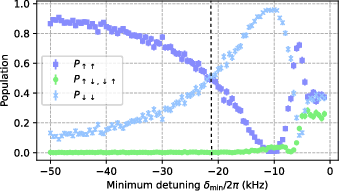
- Gate library entry “SmoothMS(θ)” where θ is compiled to δ_min; single‑parameter calibration routine based on matching P↑↑≈P↓↓ (Fig. 2).
- Built‑in carrier phase inversion mid‑gate for dynamical decoupling.
- Assumptions/dependencies: Near‑field microwave or RF magnetic‑gradient hardware; precise frequency control (kHz‑level) and phase coherence; trap with controllable DC electrodes; adiabaticity condition maintained during ramps; modest increase in gate time (~200–250 μs) acceptable for target workloads.
- Drop resolved‑sideband cooling from many circuits
- Sectors: Quantum hardware operations, scheduling, cloud services
- Use case: Run entire circuits with only Doppler cooling; the gate error remains ≲5×10-4 up to n̄≈9 (Fig. 5), enabling higher throughput and simpler job pipelines.
- Tools/products/workflows: “No‑SBC” execution mode; transport waveforms retuned for higher allowable heating; simplified calibration scripts (no sideband cooling).
- Assumptions/dependencies: Algorithm depth/error budget compatible with ~1e-4–5e-4 two‑qubit errors; motional heating rates manageable at the target transport speeds.
- Simplified, robust calibration and drift tolerance
- Sectors: Quantum hardware, control software
- Use case: Single‑knob tuning (δ_min) for θ_g; robustness to motional detuning errors and kHz‑scale drifts (Fig. 4), reducing recalibration frequency and operational downtime.
- Tools/products/workflows: Auto‑tuner that scans δ_min to maximize entanglement or equalize P↑↑ and P↓↓; slow background DC shim of mode frequencies to keep δ_min in range; guard‑banding with detuning ramps that are “fast at high |δ|, slow near δ_min”.
- Assumptions/dependencies: Stable frequency control; on‑the‑fly DC updates; Pauli randomization to mitigate SPAM asymmetry during calibration.
- Subspace Leakage Error RB (SLERB) for acceptance testing and QA
- Sectors: Industry QA, academia, benchmarking standards
- Use case: Adopt SLERB to separate SU(2) vs leakage error channels, quantify memory effects by sequence‑length truncation, and diagnose spin‑motion entanglement suppression.
- Tools/products/workflows: SLERB experiment library with bootstrap CIs; dashboards reporting ε_RB and ε_leak; periodic detuning‑offset scans for robustness checks.
- Assumptions/dependencies: Ability to compile two‑qubit‑only Clifford sequences and randomize final states.
- Global drive with local DC shimming (small‑scale)
- Sectors: Quantum hardware architecture
- Use case: Broadcast the smooth gate across multiple pairs; use local DC electrodes to set zone‑specific motional frequencies to select on/off interactions and fractional‑angle gates by δ_min per zone.
- Tools/products/workflows: Zone‑to‑DC mapping/calibration; per‑zone detuning presets; compiler pass for angle‑by‑detuning allocation.
- Assumptions/dependencies: Sufficient DC electrode count and multiplexing; acceptable cross‑talk; moderate system size.
- Noise spectroscopy and system identification
- Sectors: Quantum hardware R&D
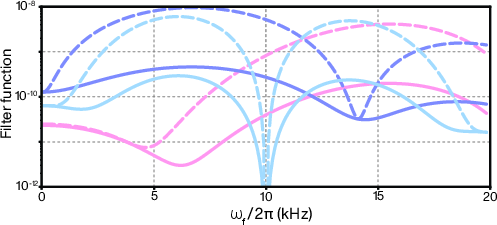
- Use case: Use the smooth gate’s low‑frequency filter function advantage to diagnose slow motional frequency noise and quantify improvements relative to Walsh sequences (Fig. 3).
- Tools/products/workflows: P_leak vs injected detuning perturbations; inference of noise PSD at sub‑kHz–kHz; feedback to trap design and shielding.
- Assumptions/dependencies: Access to AWG‑injected, calibrated detuning modulations.
- Lower barrier to entry for teaching labs and prototyping
- Sectors: Education, academia
- Use case: Build microwave‑only trapped‑ion demonstrations without sideband‑cooling lasers; run entangling gates at Doppler temperatures with simple calibration.
- Tools/products/workflows: Compact microwave gradient package; minimal‑laser optical set (Doppler cooling + detection); open‑source smooth‑gate control scripts.
- Assumptions/dependencies: Species and trap compatible with microwave gradient gates; manageable heating in the chosen environment (cryo or well‑engineered room‑temperature traps).
- Compiler and scheduler integration
- Sectors: Software, toolchains
- Use case: Integrate “θ via δ_min” mapping; schedule τ_g and τ_d ramp segments; compile mid‑gate carrier inversion; optionally bias angle control toward detuning (not amplitude) changes.
- Tools/products/workflows: Hardware‑aware gate models; cost functions that penalize amplitude ramps and prefer detuning ramps; noise‑aware placement that balances mode crowding.
- Assumptions/dependencies: Accurate hardware timing models; backend APIs for dynamic frequency control.
Long‑Term Applications
These require additional scale‑up, engineering, or validation, but are plausibly enabled by the paper’s innovations.
- Fault‑tolerant trapped‑ion QCs with low overhead
- Sectors: Quantum computing at scale (cross‑industry impact: healthcare, materials/energy, finance)
- Use case: Combine ~1e-4 two‑qubit error rates with qLDPC or comparable codes; exploit AESE‑based robustness for stable, uniform gates across many zones; enable deeper NISQ circuits (tens of thousands of gates) and earlier QEC break‑even.
- Tools/products/workflows: Large‑scale DC multiplexing for local shims; global microwave drives; active motional frequency tracking; QEC pipelines (syndrome extraction with smooth gates).
- Assumptions/dependencies: Maintain <1e-4 error in large systems; manage mode crowding and cross‑talk; robust transport and junction operations under higher n̄.
- Fully Doppler‑limited QCCD architectures with order‑of‑magnitude speedups
- Sectors: Quantum hardware architecture, cloud services
- Use case: Eliminate sub‑Doppler cooling stages from the critical path; relax transport‑heating constraints; speed up circuit execution by >10× compared to SBC‑dominated pipelines.
- Tools/products/workflows: Transport waveforms designed for higher allowable n̄; continuous DC shimming; fast detuning‑ramp controllers; scheduler that co‑optimizes transport and gating.
- Assumptions/dependencies: Heating and dephasing compatible with AESE gates at elevated n̄; reliable cryo or low‑heating room‑temperature operation.
- “Global drive, local detuning” chips that reduce wiring and optical complexity
- Sectors: Hardware manufacturing, microfabrication
- Use case: Broadcast smooth gates, select interactions by local mode frequency offsets via on‑chip DC electrodes; perform fractional‑angle gates by δ_min control instead of amplitude control; drastically reduce number of individually phased RF/microwave lines and high‑power lasers.
- Tools/products/workflows: On‑chip DC multiplexers; precision DACs; wafer‑level trap designs with integrated microwave gradient structures.
- Assumptions/dependencies: Stable and reproducible local DC control; mitigated cross‑zone coupling; robust fabrication yields.
- Energy, cost, and reliability advantages for data‑center‑grade QPUs
- Sectors: Cloud/datacenter operations
- Use case: Lower laser count/power (no SBC), fewer alignment constraints, simpler optical stacks; improved MTBF and serviceability; reduced OpEx/CapEx per qubit.
- Tools/products/workflows: Microwave‑centric modules; automated δ_min calibration; “no‑SBC” service tier.
- Assumptions/dependencies: Equivalent or better throughput under Doppler‑limited operation; scalable packaging for microwave delivery.
- Cross‑platform adiabatic‑ramp control motifs
- Sectors: Quantum platforms beyond trapped ions (where applicable)
- Use case: Translate “adiabatic elimination of residual entanglement via detuning ramps” to:
- Laser‑based MS gates (benefit limited by laser intensity noise).
- Rydberg neutral atoms (adiabatic chirps for robust phase accumulation).
- Superconducting qubits (adiabatic flux‑frequency chirps in parametric two‑qubit gates).
- Hybrid opto‑/electro‑mechanical systems (force‑drive with frequency ramps).
- Tools/products/workflows: Platform‑specific ramp synthesis and filter‑function modeling.
- Assumptions/dependencies: Existence of a controllable detuning axis with low‑noise drive; platform‑specific non‑idealities (e.g., photon scattering) do not dominate.
- Advanced control and monitoring stack
- Sectors: Control electronics, software
- Use case: Real‑time, low‑latency frequency‑ramp synthesizers; closed‑loop δ_min tracking via quick SLERB‑style probes; Bayesian/ML calibration of δ(t); continuous leakage monitors in production.
- Tools/products/workflows: Multi‑tone, phase‑coherent DDS/SDR backends; embedded calibrators; filter‑function‑aware scheduling.
- Assumptions/dependencies: Tight PHY‑level integration; fast measurement and feedback cycles.
- Benchmarks and certification standards
- Sectors: Policy/standards, procurement
- Use case: SLERB‑based vendor certification that reports ε_RB, ε_leak, and memory effects; filter‑function disclosure vs noise PSD; “Doppler‑capable” certification for two‑qubit gates.
- Tools/products/workflows: Open test suites; reference implementations and reporting templates.
- Assumptions/dependencies: Community buy‑in; cross‑vendor comparability.
- Application‑level impact as hardware matures
- Sectors: Healthcare (drug discovery), materials/energy (catalysts, batteries), finance (optimization), logistics
- Use case: Deeper, more reliable NISQ circuits now; earlier transition to QEC‑enabled workloads later; improved time‑to‑solution for VQE/QAOA variants due to higher gate count at fixed error budget.
- Tools/products/workflows: Algorithm compilers that parametrize entangling angles via δ_min; error‑mitigation routines that exploit reduced leakage.
- Assumptions/dependencies: Concurrent growth in qubit count/connectivity; algorithms that leverage higher depth and lower leakage.
Notes on feasibility across applications:
- The largest benefits accrue with electronic (laser‑free) gates, where Lamb‑Dicke and photon‑scattering limits are negligible and phase noise is low; laser‑based gates will gain robustness to detuning fluctuations but remain constrained by intensity‑related noise.
- Adiabaticity must be respected throughout the ramp; multi‑mode spacing and DC tuning ranges need to be engineered so that the least‑detuned mode determines the ramp, and others are even more adiabatic (as shown theoretically).
- The demonstrated parameters (Ω_g≈2π×6 kHz; δ_max≈−2π×400 kHz; δ_min≈−2π×22 kHz; t_g≈226 μs) provide a concrete starting point for replication, with further co‑optimization of δ(t) and scheduling likely to improve performance.
Glossary
- AC Stark shift: A shift in atomic energy levels due to off-resonant electric fields; can induce qubit frequency errors. "off-resonant AC Stark or AC Zeeman shifts."
- AC Zeeman shift: A magnetic-field-induced shift in energy levels from oscillating fields; can cause qubit frequency errors. "off-resonant AC Stark or AC Zeeman shifts."
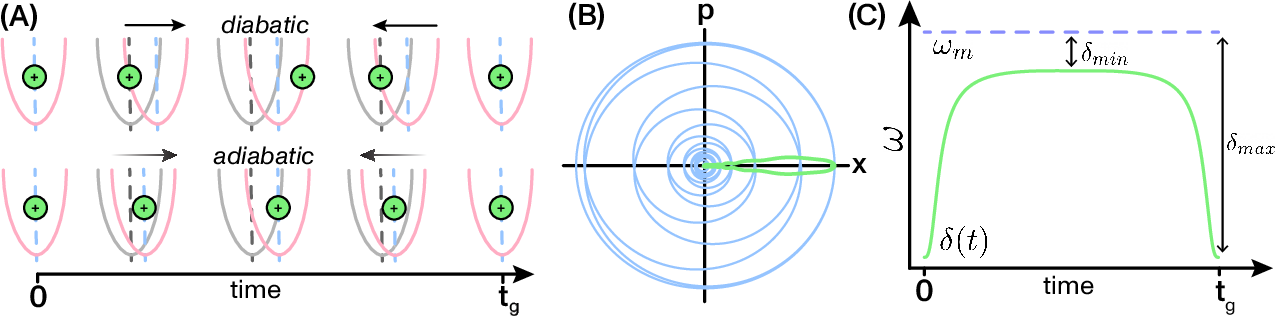
- Adiabatic elimination of spin-motion entanglement (AESE): A gate method that suppresses residual spin–motion coupling by slowly varying control parameters so the motion follows equilibrium. "To achieve this `adiabatic elimination of spin-motion entanglement' (AESE), we do the same thing as adiabatic transport: adjust the equilibrium position slowly relative to the oscillator frequency (in the frame of Eq.~(\ref{eq:geo_general_lab}))."
- Adiabaticity condition: The criterion ensuring the system changes slowly enough to avoid diabatic excitations. "We neglected the diabatic term in the second line, assuming: "
- Bichromatic oscillating current: A two-tone microwave/ RF drive at symmetric detunings used to generate spin-dependent forces for MS gates. "using a bichromatic oscillating current at frequencies which implements a M\o lmer--S\o rensen (MS) drive."
- Clifford operations: A set of unitary operations forming the Clifford group; used in randomized benchmarking. "a sequence of Clifford operations on the SU(2) subspace spanned by and "
- Detuning (gate detuning): The frequency offset between the spin-dependent force and the motional mode. "The gate detuning may be time-dependent, and may be adjusted by changing either the gate mode frequency or the gradient frequency."
- Displacement operator: A unitary that shifts the position/momentum (phase-space) of a harmonic oscillator. "we use the displacement operator: "
- Doppler cooling: Laser cooling technique bringing ions near the Doppler limit of temperature. "Each experimental shot starts with Doppler cooling via a $397$~nm laser beam $13$~MHz red-detuned from the transition"
- Doppler limit: The minimum temperature achievable via Doppler cooling set by photon recoil and linewidth. "trapped-ion quantum computation can be performed with high fidelity at temperatures above the Doppler limit"
- Dynamical decoupling: A technique using continuous or pulsed drives to average out slow noise in qubit frequencies. "An additional low-power carrier current at provides dynamical decoupling from errors due to qubit frequency fluctuations \cite{harty_2016}."
- Entanglement angle (): The geometric phase accumulated to produce a desired two-qubit entangling strength. "we must also calibrate the gate's entanglement angle , which changes ."
- Filter function: A frequency-domain measure of a control’s sensitivity to noise versus frequency. "we then obtain the filter function by calculating the infidelity (averaged over ) and dividing by ."
- Forced states: Spin eigenstates that experience a nonzero spin-dependent force during a geometric phase gate. "the forced states project the Hamiltonian onto:"
- Gate mode frequency (): The motional mode frequency used by the entangling gate. "The spin-dependent force is in general detuned from resonance with the gate mode frequency by the gate detuning ."
- Geometric phase gate: An entangling gate generated by trajectories in motional phase-space producing spin-dependent phases. "The most common method for implementing entangling gates in modern trapped-ion QCs is the geometric phase gate"
- Interaction picture: A frame splitting free evolution and interactions to simplify time-dependent Hamiltonians. "Written in the interaction picture with respect to , the Hamiltonian takes the form:"
- Lamb-Dicke effects: Higher-order coupling effects arising from motion outside the Lamb–Dicke regime; can cause temperature sensitivity. "replacing lasers with near-field magnetic field gradients makes the Lamb-Dicke effects negligible"
- Leakage error rate (): The probability per gate of leaving the target computational subspace. "obtain the
leakage error rate' and theSU(2) error rate' " - M\o lmer–S\o rensen (MS) gate: A two-qubit entangling gate using bichromatic fields coupling spin and motion. "for a M\o lmer-S\o rensen gate \cite{molmer_1999,molmer_2000}, where is the qubit frequency"
- Non-Markovianity: Memory effects where error rates depend on sequence length/history rather than being time-independent. "allows characterization of non-Markovianity at the level."
- Null states: Spin eigenstates with zero eigenvalue under the collective operator; they feel no spin-dependent force. "while the null states project it onto:"
- Pauli randomization: Randomizing final measurement axes via extra rotations to desensitize SPAM asymmetries. "providing first-order insensitivity to any asymmetry in SPAM errors between the two states (Pauli randomization)."
- Photon scattering: Undesired absorption/emission events from laser fields causing decoherence and errors. "making photon scattering negligible."
- Power spectral density: Distribution of noise power over frequency used to predict gate error via filter functions. "the noise power spectral density decays as "
- QCCD (quantum charge-coupled device): An architecture where ions are shuttled through zones to execute circuits. "quantum charge-coupled device (QCCD) trapped-ion architectures"
- Quantum error correction thresholds: Target error rates below which fault-tolerant QEC can succeed. "error rates commensurate with quantum error correction thresholds"
- Rabi frequency (): The rate of driven spin-motion coupling determining gate strength. " is the gate Rabi frequency"
- Rotating frame: A frame transformation rotating with the oscillator to simplify dynamics or visualization. "after transforming into the rotating frame with respect to the ions' bare harmonic motion (blue spiral)"
- Sideband cooling: Cooling method using resolved motional sidebands to reach near-ground-state occupation. "performing sideband cooling directly after Doppler cooling"
- Smooth gate: An entangling gate that ramps detuning smoothly to adiabatically suppress spin-motion entanglement. "We introduce the ``smooth gate'': a novel entangling gate method for trapped-ion qubits"
- Spin-motion entanglement: Unwanted residual coupling between spin states and motional states after a gate. "residual spin-motion entanglement errors"
- Subspace Leakage Error Randomized Benchmarking (SLERB): RB protocol focusing on leakage from a chosen subspace to estimate gate errors. "We assess the performance of the smooth gate using Subspace Leakage Error Randomized Benchmarking (SLERB)"
- SU(2) subspace: The two-dimensional subspace spanned by symmetric two-qubit states used for subspace RB. "on the SU(2) subspace spanned by and "
- Walsh modulation: A composite-pulse technique using Walsh functions to suppress sensitivity to detuning/timing errors. "Techniques such as Walsh modulation \cite{hayes_2012} are often employed to suppress these errors"
- ZZ gate: An entangling interaction implementing a σ_z⊗σ_z coupling via near-resonant motion. "or for a ZZ gate \cite{leibfried_2003, srinivas_2021}."
Collections
Sign up for free to add this paper to one or more collections.