- The paper introduces DLER, a reinforcement learning framework that optimizes token usage with batch-wise reward normalization and dynamic sampling.
- It addresses biases in advantage estimation, entropy collapse, and sparse rewards, reducing token output by up to 70% without accuracy loss.
- Experimental results on benchmarks like MATH and Olympiad validate improved accuracy-length trade-offs and robust efficiency gains.
Incentivizing More Intelligence per Token via Reinforcement Learning
Introduction
The paper "DLER: Doing Length pEnalty Right - Incentivizing More Intelligence per Token via Reinforcement Learning" (2510.15110) introduces a novel framework to enhance the efficiency of reasoning LLMs by optimizing the reinforcement learning (RL) procedure, rather than relying on complex length penalties. Recent developments in RL for reasoning models have aimed to reduce the output lengths generated by models like DeepSeek-R1 and OpenAI-o1, addressing a key concern: maximizing intelligence per token. The proposed DLER approach implements batch-wise reward normalization, higher clipping, dynamic sampling, and a straightforward truncation length penalty, showcasing substantial improvements in accuracy-length trade-offs and operational efficiency.
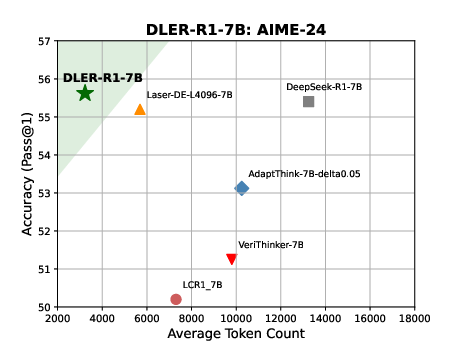

Figure 1: DLER achieves state-of-the-art accuracy/length trade-offs, shortening CoT by up to 70% without losing accuracy.
Challenges in Reinforcement Learning Optimization
The paper identifies three significant challenges inherent in current RL techniques applied to reasoning models:
Biased Advantage Estimation: GRPO-based advantage estimation is heavily impacted by reward noise, resulting in inaccurately calculated advantages due to frequent zero-reward assignments.
Entropy Collapse: This phenomenon severely limits exploration of diverse reasoning paths, as the model struggles to maintain output distribution diversity, which is essential for effective learning.
Sparse Reward Signals: The prevalence of zero rewards due to truncation causes the model to favor easily solvable prompts, thus hindering effective learning on complex tasks.
To counter these problems, DLER integrates a normalized batch-wise reward system and dynamic sampling, gradually filtering prompts to enhance learning efficacy.

Figure 2: Uniform batch-wise reward normalization maintains stability and accuracy, in contrast to GRPO's declining performance.
DLER Training Recipe
DLER combines several elements to enhance RL optimization:
- Batch-wise Reward Normalization: Stabilizes advantage estimation, mitigating biases linked to high variance rewards.
- Higher Clipping Thresholds: Retains gradient propagation for high-entropy token updates, fostering exploration.
- Dynamic Sampling: Filters prompts to maintain balanced training signals, reducing the influence of skewed distributions.
The comprehensive application of these strategies enables substantial improvements in both accuracy and token efficiency, fully recovering accuracy while drastically reducing token usage.
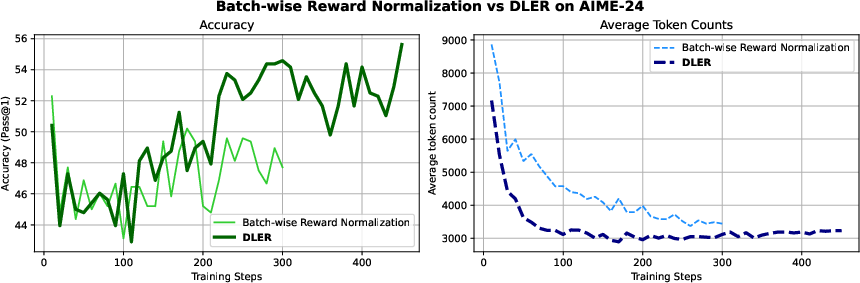
Figure 3: DLER enhances efficiency by reducing token usage and recovering accuracy loss of applying plain batch-wise reward normalization.
Difficulty-Aware DLER
The paper further extends the DLER framework with a difficulty-aware mechanism, DA-DLER, which dynamically adjusts truncation lengths based on prompt difficulty. This refinement allows the model to dedicate fewer tokens to simpler questions, thereby enhancing overall efficiency without sacrificing accuracy on more complex tasks.
Experimentation and Results
DLER models exhibit consistent superiority over competing baselines, notably achieving enhanced reasoning efficiency across diverse benchmarks like MATH, AIME-24, and Olympiad Bench. These results validate the framework's robustness and illustrate the practical benefits of optimized RL strategies over complex penalty design.

Figure 4: Ratio of prompts with zero rewards and prompt shortening patterns observed during training phases.
Implications and Future Directions
The introduction of DLER marks a significant shift towards optimizing reasoning efficiency by refining RL algorithms, rather than merely adjusting penalty designs. This perspective invites further exploration into adaptive RL strategies that can dynamically modulate resource allocation based on contextual difficulty. Moreover, the successful integration of update-selective merging strategies provides a pathway for leveraging publicly available datasets without compromising accuracy, offering a practical solution for deploying efficient reasoning models in resource-constrained settings.
Conclusion
The study redefines the approach to enhancing reasoning efficiency in LMs, emphasizing RL optimization techniques over complex length penalties. Findings demonstrate how intelligent adjustment of RL processes can substantially improve the trade-off between reasoning capability and token consumption. Future efforts can further explore adaptive optimization algorithms to push the boundaries of efficiency in reasoning models, promising advancements in both practical and theoretical AI applications.






