Noise-Adaptive Layerwise Learning Rates: Accelerating Geometry-Aware Optimization for Deep Neural Network Training (2510.14009v1)
Abstract: Geometry-aware optimization algorithms, such as Muon, have achieved remarkable success in training deep neural networks (DNNs). These methods leverage the underlying geometry of DNNs by selecting appropriate norms for different layers and updating parameters via norm-constrained linear minimization oracles (LMOs). However, even within a group of layers associated with the same norm, the local curvature can be heterogeneous across layers and vary dynamically over the course of training. For example, recent work shows that sharpness varies substantially across transformer layers and throughout training, yet standard geometry-aware optimizers impose fixed learning rates to layers within the same group, which may be inefficient for DNN training. In this paper, we introduce a noise-adaptive layerwise learning rate scheme on top of geometry-aware optimization algorithms and substantially accelerate DNN training compared to methods that use fixed learning rates within each group. Our method estimates gradient variance in the dual norm induced by the chosen LMO on the fly, and uses it to assign time-varying noise-adaptive layerwise learning rates within each group. We provide a theoretical analysis showing that our algorithm achieves a sharp convergence rate. Empirical results on transformer architectures such as LLaMA and GPT demonstrate that our approach achieves faster convergence than state-of-the-art optimizers.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Plain‑Language Summary of the Paper
What is this paper about?
This paper is about teaching big neural networks (like GPT and LLaMA) to learn faster and more safely. The authors noticed that different parts (layers) of these networks behave differently and change over time during training. So, they built a method that automatically gives each layer its own “right-sized” learning rate that adapts to how noisy or stable that layer’s signals are. They call this method LANTON.
What questions are they trying to answer?
- Can we speed up training by letting each layer in a neural network have its own learning rate that adapts over time?
- Can we do this in a “geometry‑aware” way, meaning we respect the different shapes and roles of parameters (matrices vs. vectors, attention layers vs. embeddings)?
- Will this approach work better than popular optimizers (like AdamW, Muon, and others) on real models such as GPT2 and LLaMA?
- Can we prove, in theory, that this method converges (gets better) quickly even when there’s randomness (noise) in training?
How does their method work? (Simple explanation)
Think of training a neural network like guiding a team of cyclists down a hill:
- The “learning rate” is how big a step each cyclist takes.
- Each layer is a different cyclist—some are on smooth road, some on bumpy gravel.
- If everyone uses the same speed (learning rate), the cyclists on gravel slip or wobble. Others on smooth road go too slow.
The idea: measure how “bumpy” (noisy) the path is for each cyclist (layer), then set each one’s speed to match the road. Bumpier layer → smaller steps; smoother layer → bigger steps.
How they do it, in practice:
- They compute the gradient (the direction to go downhill) for each layer at every training step.
- They estimate how noisy each layer’s gradient is. In simple terms, they look at how much the gradient changes between steps. Big changes = more noise.
- They turn that noise estimate into a scaling factor that shrinks or grows the learning rate for that layer.
- They plug this into a “geometry‑aware” optimizer. Geometry‑aware means it treats different parameter types according to their natural shape and role (for example, large weight matrices in attention layers vs. vectors in normalization). This uses a tool called an LMO (Linear Minimization Oracle), which you can think of as “pick the best direction to move if you’re only allowed to move in certain ways.”
Helpful analogies for technical terms:
- Geometry‑aware: using the right tool for each part (like using a wrench for bolts and a screwdriver for screws), instead of one tool for everything.
- Noise (gradient variance): wiggliness caused by randomness when you train on small batches of data.
- Dual norm: a matching ruler used to measure noise in the same “units” as the update rule, so the measurements and movements fit together.
The method is called LANTON. It:
- Tracks per‑layer noise with a smoothed moving average.
- Converts that noise into a per‑layer learning‑rate multiplier.
- Works with existing geometry‑aware optimizers like Muon, SCION, and D‑Muon.
What did they find?
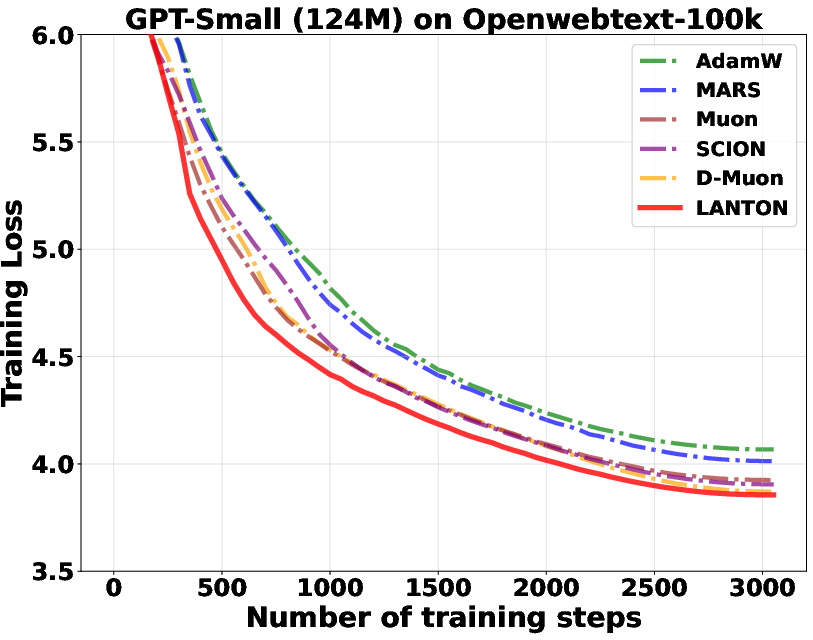
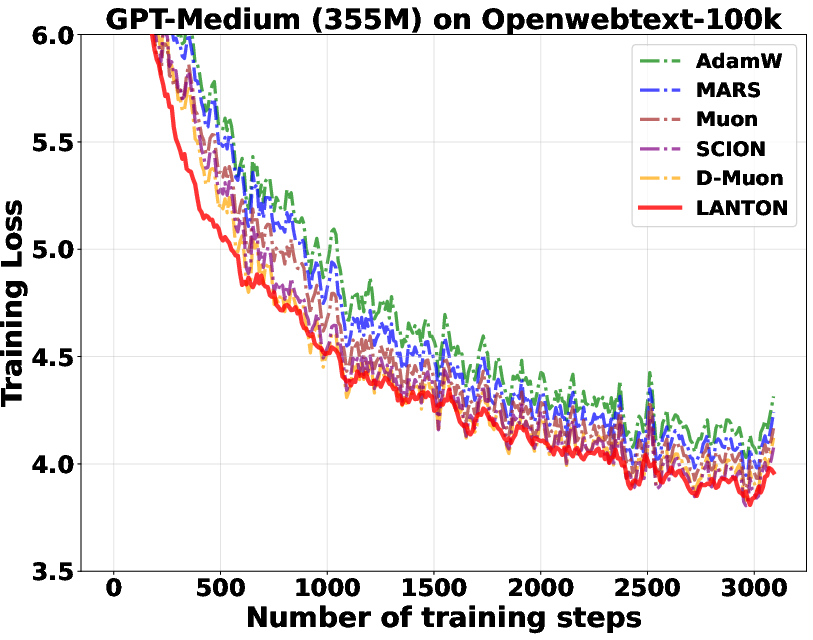
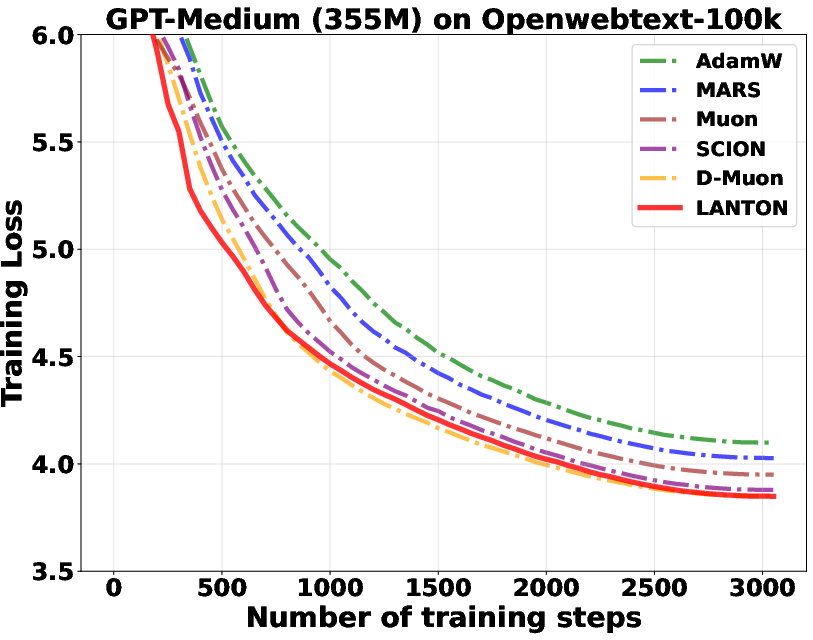
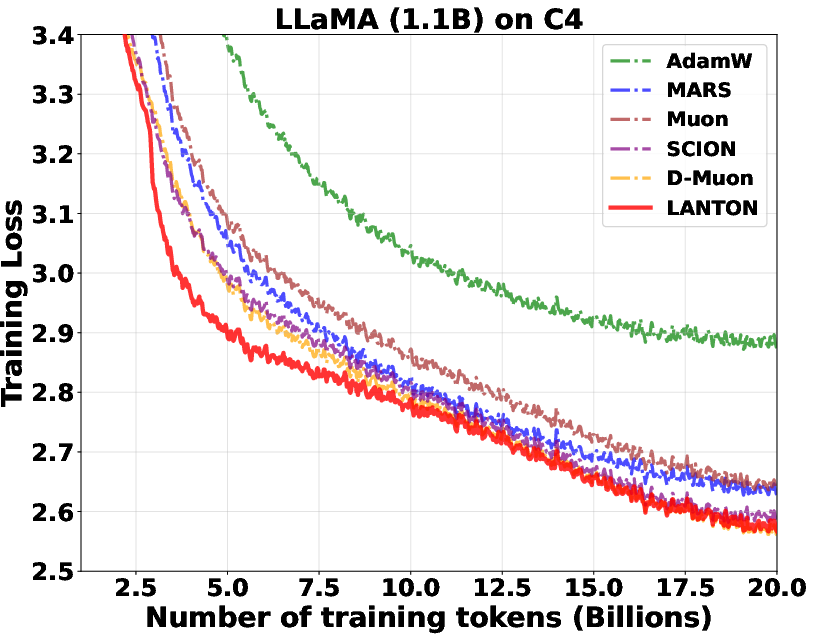
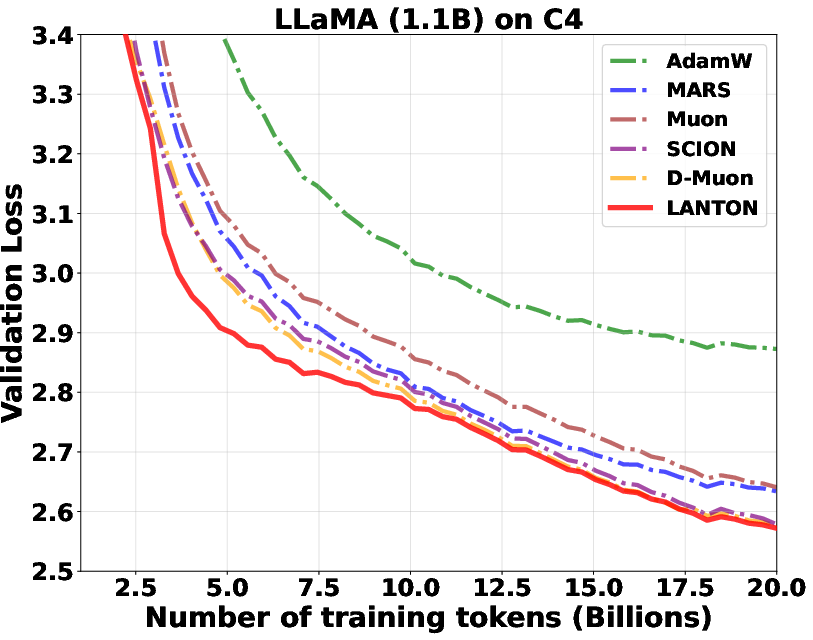
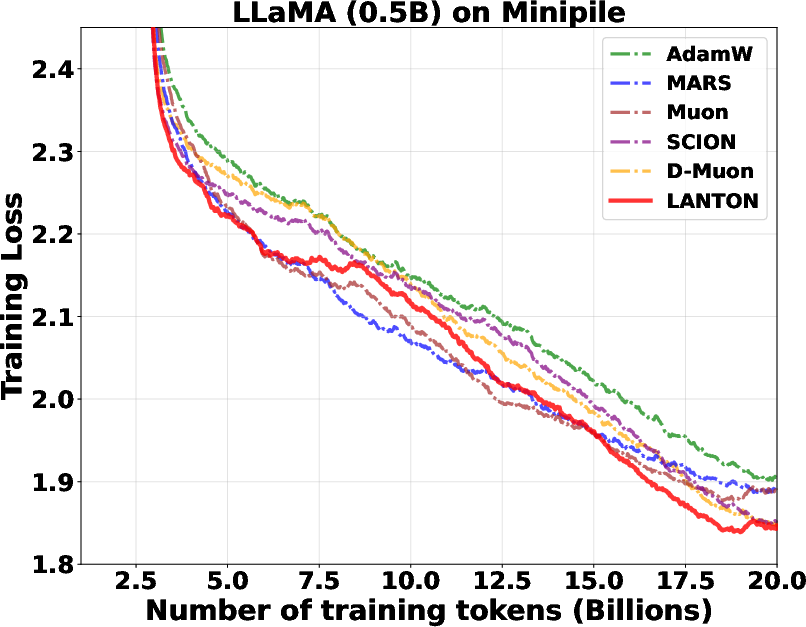
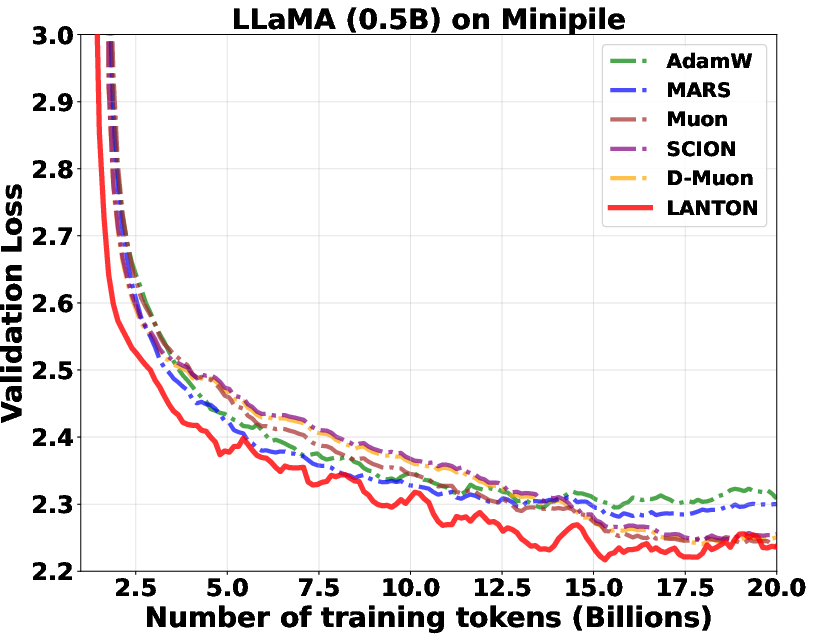
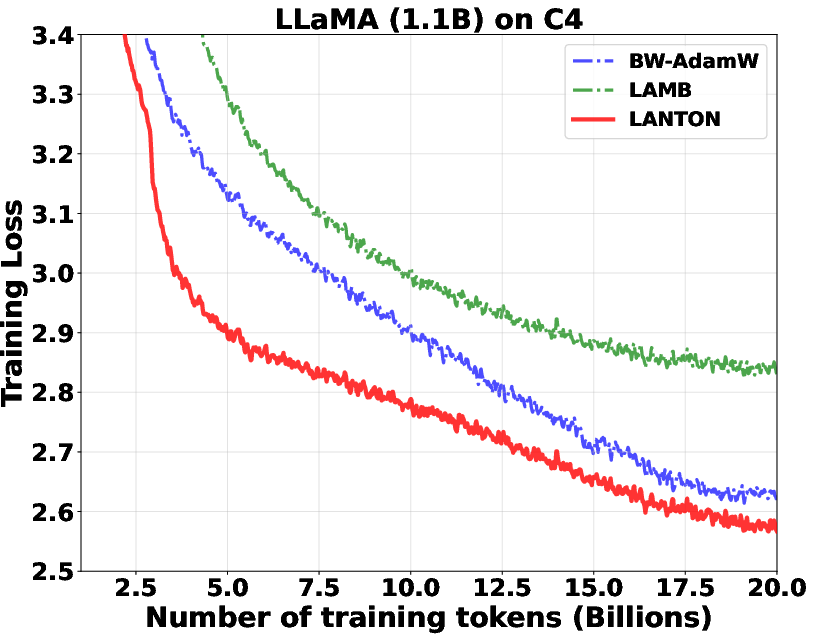
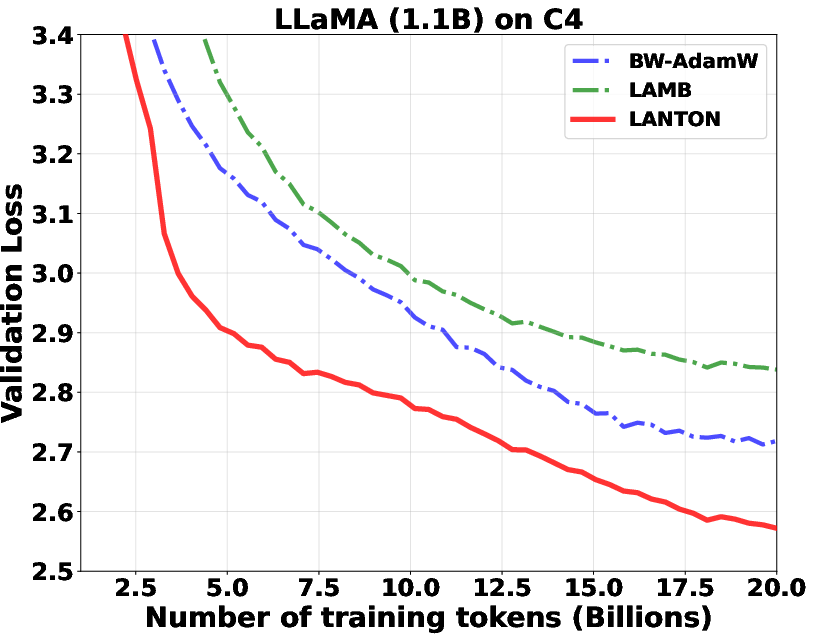
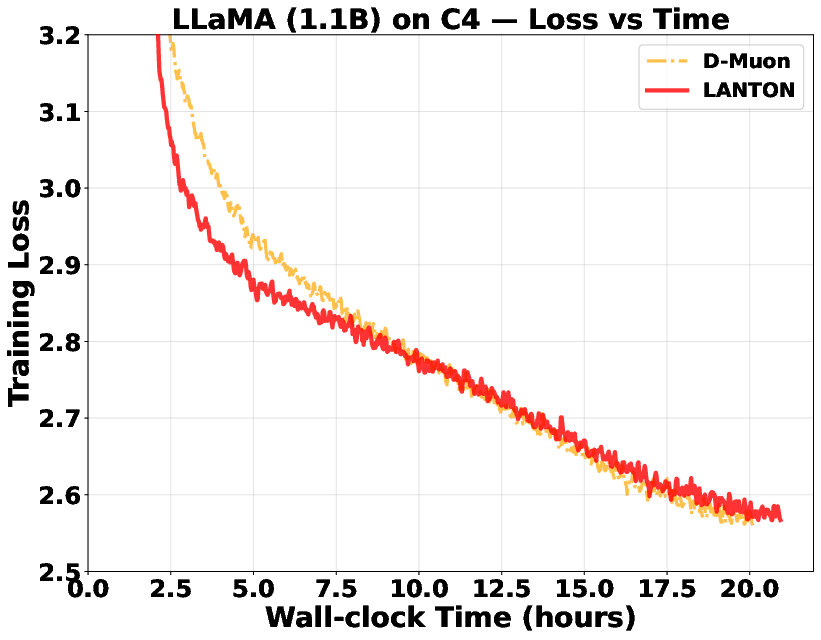
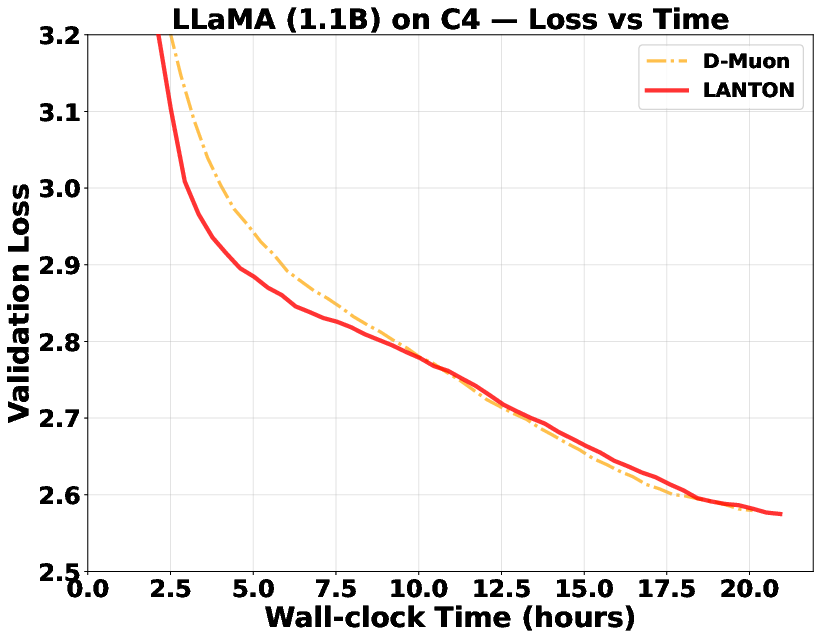
- In experiments on transformer models (GPT2 and LLaMA), LANTON made training faster and more sample‑efficient:
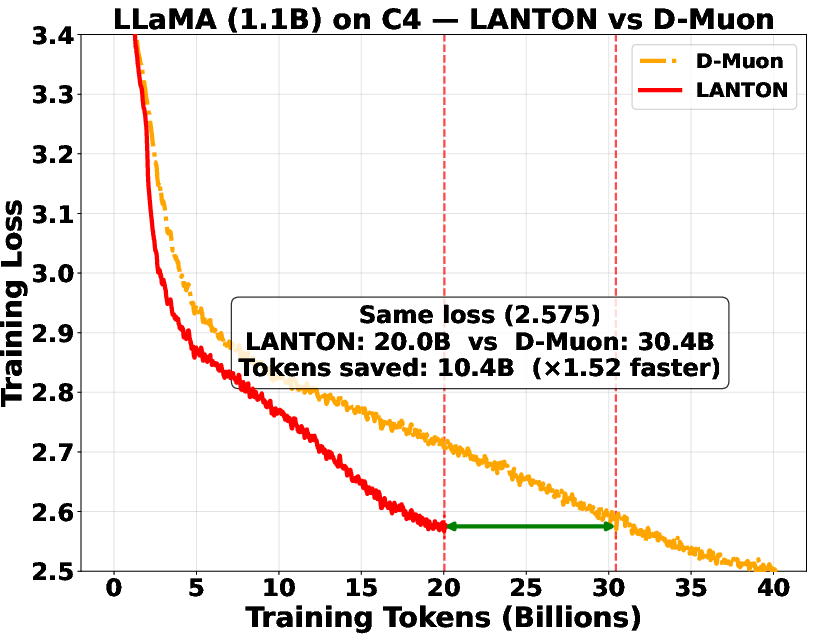
- It reached the same training or validation loss about 1.5× faster than a strong baseline (D‑Muon).
- In a fixed token budget test, a baseline needed about 1.5× more data to catch up to LANTON’s loss.
- It worked better than methods that use fixed layer‑wise or block‑wise learning rates because LANTON adapts on the fly to each layer’s changing noise.
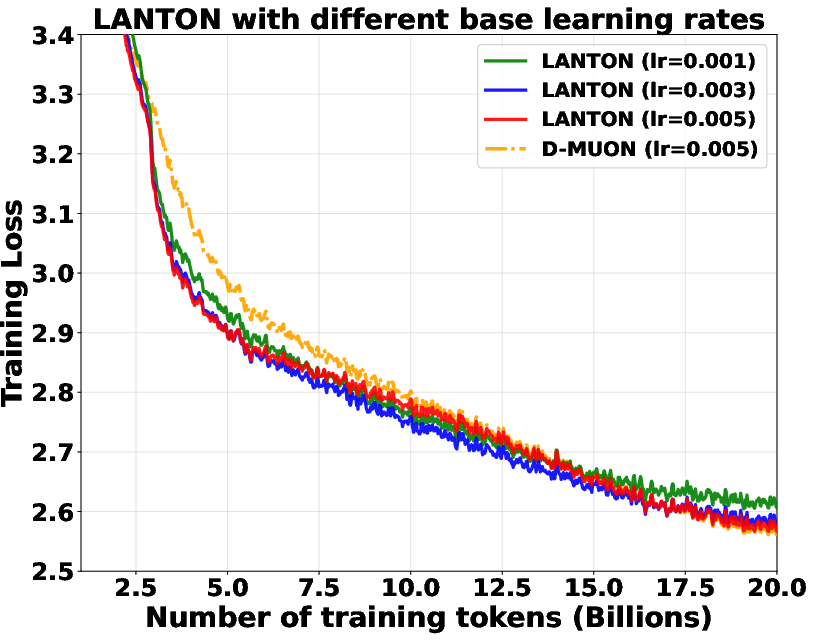
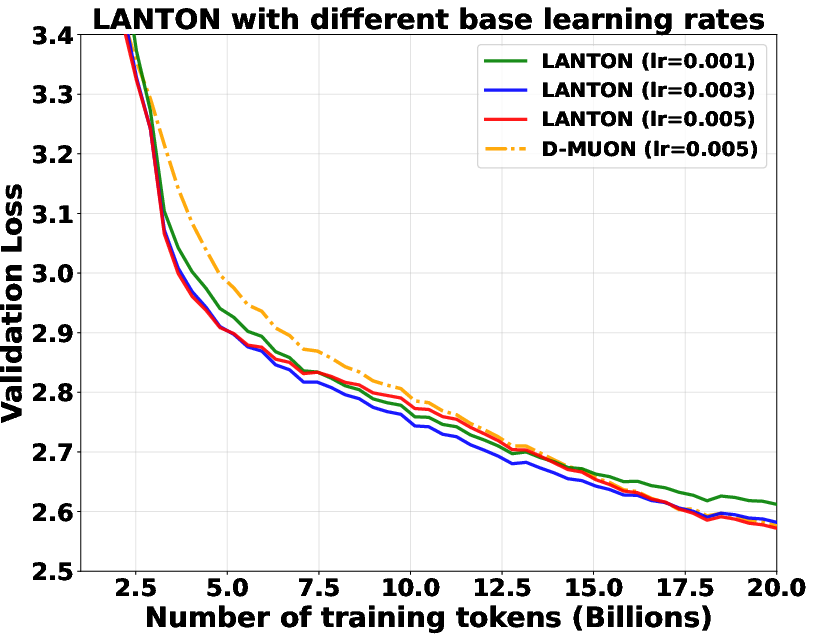
- It was reasonably robust to different base learning rates (it still trained faster or matched performance in most cases).
- The authors also provide a mathematical proof showing LANTON has a strong convergence rate. In plain terms: the algorithm’s progress stays fast even with noisy gradients, especially when only some layers are noisy. Their theory shows an improvement by taking into account that some layers are noisier than others, rather than pretending all layers are equally noisy.
Why is this important?
- Faster training: Big models are expensive to train. Speeding up training by even 1.5× saves time and money.
- Better stability: Noisy layers get gentler updates, reducing the chance of training “blow‑ups.”
- Smarter adaptation: Layers in transformers behave differently (and change over time). This method responds to those differences automatically.
- Plug‑and‑play: It works on top of leading geometry‑aware optimizers, so it can be adopted without throwing away existing systems.
What could this lead to next?
- Scaling up: Testing LANTON on even larger models and datasets could bring bigger savings.
- Wider use: The idea of measuring per‑layer noise and adapting learning rates could be applied to other architectures (e.g., vision models) or mixed with other training tricks.
- Theory to practice: Refining the theory to reduce dependencies on model size and making the method even more efficient.
In short, the paper shows that paying attention to how noisy each layer is—and adjusting each layer’s learning rate accordingly, in a way that respects the shape and role of its parameters—can make large neural networks train faster and more efficiently.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored in the paper, aimed to guide future research.
- Theory–practice mismatch in noise estimation: the analysis assumes two independent gradients per layer at each step (Option II), while the implementation uses the biased proxy (Option I). The impact of this bias on convergence and stability is unquantified.
- Assumption of a strictly positive lower bound on layer-wise noise () is strong and may be violated (e.g., near convergence or in deterministic phases). How to relax or replace this assumption while retaining guarantees remains open.
- Hyperparameter choices in the theorem (e.g., , , ) depend on unknown quantities (, , ) that are not observable in practice; a principled, data-driven selection strategy with theoretical backing is missing.
- Dimension-dependent constants (, ) in the bounds are unspecified and potentially large; their values under the paper’s chosen norms and architectures and their practical effect on rates are not characterized.
- Convergence guarantees assume exact LMO solutions, but hidden-layer LMOs are approximated via finite Newton–Schulz steps. The effect of LMO approximation error on convergence and the required number of iterations for reliable performance are not analyzed.
- The estimator conflates stochastic noise with drift due to loss curvature and parameter updates (when using ). A de-biased estimator (e.g., via extra mini-batch or control variates) and its cost–benefit tradeoff are not studied.
- The choice of group-level normalization and scaling is not theoretically justified or compared to alternatives (mean, median, clipped averages, different exponents). Ablations are missing.
- Sensitivity to the choice of norms per group (RMS→RMS for hidden layers, for embeddings/LM head, RMS for vectors) is not evaluated; guidance or automatic norm selection mechanisms are absent.
- It is unclear whether noise-adaptive scaling was fully applied to non-matrix groups (embedding/LM head and LayerNorm vectors) in all experiments; a clear, unified implementation and its impact across groups is not documented.
- Weight decay () appears in inputs but is not integrated into the LMO-based update rule for hidden layers. How to correctly incorporate decoupled weight decay into geometry-aware, LMO-driven updates is unresolved.
- Robustness to batch size and large-batch regimes (where gradient noise scales differently) is not investigated; interaction with LARS/LAMB-like trust ratios or layer-wise clipping remains open.
- Interaction with gradient clipping, dropout, mixed precision, and other common training techniques is not analyzed; how these affect noise estimation in dual norms and the stability of Newton–Schulz iterations is unknown.
- Computational and communication overheads at scale are not quantified: extra dual-norm computations, per-layer buffers, Newton–Schulz iterations, and groupwise reductions may affect throughput in multi-GPU/multi-node training.
- Wall-clock speed vs. token efficiency is not comprehensively reported in main text; the practical tradeoff between faster loss reduction per token and actual training time (including LMO compute) needs systematic measurement.
- The approach is only validated on moderately sized transformer decoders (GPT2-small/medium; LLaMA-0.5B/1.1B). Performance, stability, and scalability on substantially larger models (e.g., >7B parameters) and longer sequence lengths remain open.
- Generalization beyond validation loss is not assessed (e.g., downstream tasks, zero-shot/finetuning performance, perplexity on standardized benchmarks). Whether noise-adaptive geometry-aware updates improve downstream outcomes is unknown.
- Comparisons exclude several strong modern baselines (e.g., Sophia, SOAP, Shampoo variants, schedule-free AdamW) that target efficiency; a broader empirical paper is necessary to contextualize gains.
- Lack of ablations to separate the effects of noise adaptivity from other design choices (norm selection, LMO implementation, group scaling factors , ). Causal attribution for observed speedups is incomplete.
- Theoretical smoothness assumptions (layer-wise -smoothness under non-Euclidean norms) are not validated for typical transformer layers; empirical or theoretical verification of under the chosen norms is missing.
- Correctness of the table’s LMO mappings (e.g., Signum for operator norm, RMS normalization for vectors) is not formally derived; providing proofs or precise conditions under which these are exact LMOs would strengthen the framework.
- The choice of square-root scaling in lacks theoretical derivation; exploring other functional forms and their convergence implications is an open area.
- Behavior when noise vanishes or becomes highly nonstationary: does saturate or collapse? How to prevent under-training of layers that become “noisy” or “quiet” intermittently is not addressed.
- The estimator and scaling operate on per-layer aggregates; finer granularity (per-parameter block or head) might further help but is unexplored; conversely, whether per-layer scaling can destabilize inter-layer coordination is unknown.
- Choice of Newton–Schulz iteration count (5 steps) lacks justification; the tradeoff between approximation error, compute overhead, and empirical gains is not characterized.
- Formal guidance for setting is limited; a principled tuning protocol or adaptive schedule (potentially schedule-free) is absent.
- Dataset diversity is limited (C4, MiniPile, OpenWebText-100k). Extending to multilingual corpora, code, or multimodal data and evaluating robustness across data regimes is an open direction.
- Empirical validation of the theory’s proxy metric (average dual-norm gradient) is missing; directly measuring convergence criteria aligned with the theorem in practice would strengthen the claims.
Practical Applications
Immediate Applications
Below are concrete, deployable uses of the paper’s findings and methods that can be adopted now across industry, academia, policy, and daily life.
- Faster pretraining and fine-tuning of transformer models in production
- Sector: Software, cloud AI, enterprise AI
- Use case: Replace AdamW/D-Muon/Scion optimizers in training pipelines for GPT/LLaMA-like models to achieve roughly 1.5× speedup and higher sample efficiency at comparable loss.
- Tools/workflows: A PyTorch optimizer plugin implementing LANTON with per-layer LMOs (Newton–Schulz for hidden layers, Signum for embeddings/LM head, RMS normalization for RMSNorm vectors), layerwise noise tracking buffers, and cosine LR scheduling.
- Assumptions/dependencies: Transformer layers grouped as {QK, VO, MLP}, {Embedding, LM-Head}, {LayerNorm}; correct LMO implementations; stable hyperparameters (α, β1, β2); unbiased gradient oracle; practical noise estimator uses gradient differences across steps (Option I) rather than two independent gradients (Option II).
- Training cost and energy reduction in cloud and on-prem clusters
- Sector: Energy, cloud infrastructure, MLOps
- Use case: Cut GPU hours per experiment and reduce carbon footprint by converging in fewer tokens/steps; prioritize LANTON for costly pretraining runs.
- Tools/workflows: “Optimizer-aware schedulers” in DeepSpeed/Accelerate that select LANTON for transformer blocks; billing dashboards that track tokens-to-loss efficiency.
- Assumptions/dependencies: Works best for transformer matrices; additional logging overhead to track layerwise variance buffers Htℓ.
- Sample-efficient experimentation in research and product iteration
- Sector: Academia, software product R&D
- Use case: Rapidly iterate on architectures and data curricula by reaching target validation loss with fewer tokens (e.g., ~1.5× fewer).
- Tools/workflows: Hugging Face Trainer callback that monitors layerwise gradient noise and tunes base LR bounds ηmin/ηmax to maintain stability; experiment tracking in Weights & Biases with layerwise noise panels.
- Assumptions/dependencies: Stability depends on per-layer noise estimates in dual norms; cosine schedules remain beneficial; dimension-dependent constants may affect very large models.
- Domain-specific model training at lower budgets
- Sector: Healthcare, finance, legal, ecommerce
- Use case: Pretrain/fine-tune domain LLMs (clinical NLP, document intelligence, compliance QA) on limited GPUs while retaining performance targets.
- Tools/workflows: Drop-in optimizer replacement in common stacks (PyTorch + Transformers + DeepSpeed), with a configuration file mapping layer groups to LMOs and noise buffers.
- Assumptions/dependencies: Tested on GPT2/LLaMA-scale; transfer to larger domain models should be verified; embedding/LM-head are updated via Signum, which may differ from current defaults.
- Open-source model training and hobbyist fine-tunes
- Sector: Daily life, open-source community
- Use case: Faster LoRA/full-parameter fine-tuning of small/medium transformers on consumer GPUs by adopting layerwise noise-adaptive LRs.
- Tools/workflows: A pip-installable “lanton-optimizer” module that auto-detects transformer submodules and applies the correct LMOs; preset configs for GPT2/LLaMA sizes.
- Assumptions/dependencies: LoRA adapters are low-rank matrices; mapping LoRA modules to appropriate operator norms and LMOs is needed.
- Diagnostics and observability for training stability
- Sector: MLOps, academia
- Use case: Identify noisy layers (e.g., QK vs VO vs MLP) during training and downscale their effective LR to avoid instability.
- Tools/workflows: A “Layer Noise Monitor” dashboard that logs Htℓ and the effective LR ratio αtℓ/αtm per group; alerts when noise spikes suggest learning rate reductions.
- Assumptions/dependencies: Htℓ computed in dual norms; accuracy of practical estimator using Gtℓ − Gt−1ℓ; requires instrumentation hooks.
- Curriculum/data pipeline optimization via token budgets
- Sector: Education tech, data-centric AI
- Use case: Plan training curricula to hit loss milestones with fewer tokens by using LANTON’s sample efficiency; reduce annotation or data acquisition costs.
- Tools/workflows: “Token budget planner” that forecasts loss vs tokens under LANTON vs baselines for a given architecture and dataset.
- Assumptions/dependencies: Results are strongest on transformer architectures and language datasets; data distribution shifts can change per-layer noise profiles.
- Integrating geometry-aware training into optimizer suites
- Sector: Software tooling
- Use case: Extend existing optimizer libraries (e.g., optimizers in PyTorch Lightning, Hugging Face) with geometry-aware LMOs and noise-adaptive per-layer scaling.
- Tools/workflows: A “Geometry-Aware Optimizer Suite” bundling Muon/Scion/D-Muon variants with LANTON scaling; configuration presets per architecture family.
- Assumptions/dependencies: Correct operator norm selection per layer type; Newton–Schulz iterations tuned (e.g., 5 steps) for hidden matrices.
- Policy reporting on AI energy efficiency
- Sector: Policy, sustainability
- Use case: Include optimizer choice (e.g., LANTON adoption) in organizational energy efficiency and carbon reporting as a recognized lever to reduce training emissions.
- Tools/workflows: Sustainability KPIs that track “loss per kWh” and “tokens per target loss” with optimizer annotations.
- Assumptions/dependencies: Requires standardized measurement pipelines; cross-organization comparability depends on hardware and dataset differences.
Long-Term Applications
These opportunities benefit from further research, scaling, or engineering before broad deployment.
- Scaling to multi-tenant, distributed pretraining of 10B–70B+ models
- Sector: Cloud AI, foundation models
- Use case: Use LANTON in ZeRO/FS-DP pipelines to dynamically allocate per-layer compute/communication based on noise and curvature, reducing time-to-converge at scale.
- Tools/workflows: DeepSpeed/Alpa/ColossalAI integrations with per-layer LR ratios αtℓ/αtm broadcast across workers; adaptive gradient compression tuned by noise levels.
- Assumptions/dependencies: Dimension-dependent constants may affect stability at extreme scales; need robust dual-norm implementations and communication-efficient noise tracking.
- Generalization beyond transformers to vision, diffusion, and multimodal models
- Sector: Computer vision, generative AI
- Use case: Apply operator norm LMOs to CNNs (define suitable norms for conv kernels), diffusion U-Nets, and VLMs; adapt noise-adaptive LR to heterogeneous blocks.
- Tools/workflows: Norm/LMO recipes for conv layers (e.g., RMS→RMS for kernel tensors), diffusion blocks, and cross-attention; benchmarking suite across modalities.
- Assumptions/dependencies: Requires careful norm selection and efficient LMO implementations for non-transformer layers; empirical validation on large datasets.
- Noise-aware resource scheduling and energy-optimal training
- Sector: Energy, cloud orchestration
- Use case: Cluster schedulers that modulate GPU frequency, batch size, or microbatching per layer based on real-time noise, optimizing energy per unit loss.
- Tools/workflows: “Noise-to-energy” controllers integrating LANTON signals with DVFS and gradient accumulation strategies.
- Assumptions/dependencies: Tight coupling between optimizer telemetry and hardware APIs; robust control theory to avoid oscillations.
- Automated hyperparameter tuning reduced by geometry-aware adaptivity
- Sector: AutoML
- Use case: Shrink hyperparameter search spaces by relying on LANTON’s per-layer adaptation rather than manual LR scaling or block-specific ratios.
- Tools/workflows: AutoML pipelines that treat α, β1, β2 as small search sets while fixing layer group mappings; meta-learned priors for αtℓ schedules.
- Assumptions/dependencies: Additional studies on sensitivity across architectures/datasets; standardized defaults for large-scale training.
- Robust training under non-stationary data and shifting noise profiles
- Sector: Finance, security, streaming platforms
- Use case: Maintain stability when data distributions shift (e.g., regime changes) by adapting per-layer LR in response to evolving noise and curvature.
- Tools/workflows: Streaming training frameworks with online noise tracking and adaptive LR bounds; anomaly detection on Htℓ for early warnings.
- Assumptions/dependencies: The unbiased gradient assumption may be stressed under covariate shift; need variants that incorporate variance reduction or robust estimators.
- Hardware/compiler co-design for LMOs and dual-norm computations
- Sector: Semiconductors, AI accelerators
- Use case: Accelerate Newton–Schulz iterations and dual-norm operations in compilers (e.g., Triton, XLA) or on dedicated accelerator cores.
- Tools/workflows: Kernel fusion for LMO steps, approximate SVD proxies tailored to operator norms, mixed-precision safeguards.
- Assumptions/dependencies: Numerical stability of iterative orthogonalization; hardware-specific precision constraints.
- Extensions to reinforcement learning and world models
- Sector: Robotics, autonomous systems
- Use case: Apply per-layer noise-adaptive LR to offline RL model training and transformer-based world models to improve sample efficiency and stability.
- Tools/workflows: RL libraries integrating LANTON for policy and value networks with transformer backbones; off-policy training with noise-aware LR modulations.
- Assumptions/dependencies: RL noise is non-iid and may violate some assumptions; requires adaptation of noise estimators to trajectory-based gradients.
- Governance and procurement standards recognizing optimizer efficiency
- Sector: Policy, enterprise governance
- Use case: Establish best-practice guidelines that include geometry-aware, noise-adaptive optimizers in compute procurement and sustainability strategies.
- Tools/workflows: Auditor-friendly documentation of training runs, loss-per-token metrics, and optimizer configuration transparency.
- Assumptions/dependencies: Community consensus on standardized efficiency reporting; third-party validation benchmarks.
- Curriculum and pedagogy in advanced optimization for deep learning
- Sector: Education
- Use case: Teach operator norms, LMOs, and dual-norm noise adaptivity in graduate courses; labs where students instrument and compare optimizers on real models.
- Tools/workflows: Educational notebooks demonstrating LANTON vs AdamW/Muon/D-Muon/Scion on GPT/LLaMA variants; visualization of layerwise noise heterogeneity.
- Assumptions/dependencies: Availability of GPU resources and curated datasets; simplified implementations that run in classroom environments.
Notes on feasibility and assumptions across applications:
- Theoretical guarantees depend on layer-wise smoothness and noise being bounded above and below; Option II (two independent gradients) is more theoretically aligned but doubles gradient estimation cost.
- Practical deployments typically use Option I (Gtℓ − Gt−1ℓ) for noise estimation; empirical success is reported despite relaxed independence.
- Dimension-dependent constants and LMO iteration stability (Newton–Schulz) can affect scaling; careful engineering is required for very large models.
- Layer grouping and norm choices are architecture-specific; generalization beyond transformers requires tailored operator norms and LMOs.
Glossary
- Azuma-Hoeffding inequality: A concentration inequality that bounds deviations of martingale sequences, used to obtain high-probability bounds. "Azuma-Hoeffding inequality (see \cref{lem:azuma})."
- Conditional gradient method: A projection-free optimization method equivalent to Frank-Wolfe that uses a linear minimization oracle over the feasible set. "conditional gradient method \citep{jaggi2013revisiting}"
- Cosine decay schedule: A learning-rate schedule that follows a cosine curve to gradually reduce the step size over time. "( follows a cosine decay schedule)"
- Decoupled weight decay: A regularization technique where weight decay is applied separately from the gradient update, popularized by AdamW. "AdamW \citep{loshchilov2017decoupled} introduced decoupled weight decay"
- Dual norm: For a given norm, the dual norm measures the maximum inner product with vectors of unit primal norm and is used to quantify gradient magnitudes in the dual space. "with associated dual norm "
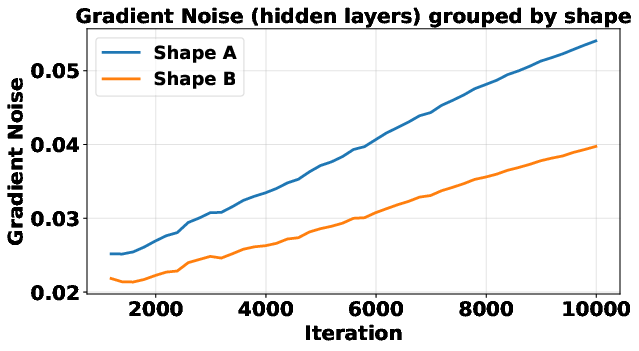
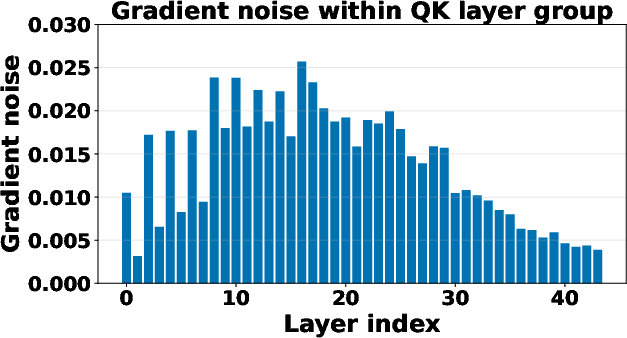
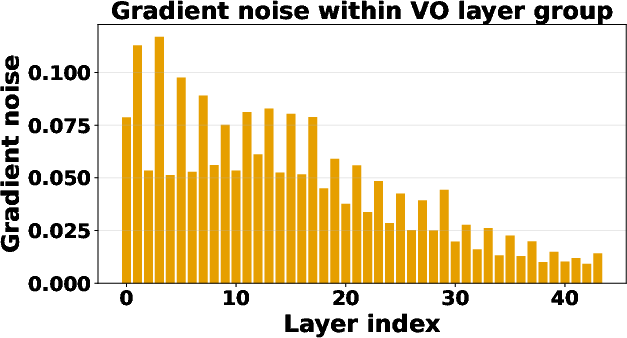
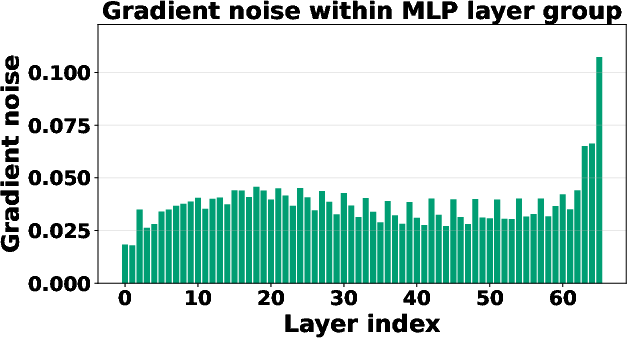
- Dual space: The space of linear functionals corresponding to a normed space; here used to describe bounds on stochastic gradient noise measured via the dual norm. "the layer-wise gradient noise is almost surely bounded both above and below in the dual space."
- Extreme point: A point in a convex set that cannot be expressed as a nontrivial convex combination of other points in the set. "the LMO returns an extreme point of $$ that minimizes the linear function"</li> <li><strong>Frank-Wolfe algorithm</strong>: A projection-free algorithm for constrained convex optimization that relies on a linear minimization oracle at each step. "Frank-Wolfe algorithm (also known as the conditional gradient method"</li> <li><strong>Geometry-aware optimization</strong>: Optimization methods that exploit parameter structure and norms (e.g., operator norms) instead of treating all parameters uniformly. "geometry-aware optimization algorithms such as Muon \citep{jordan2024muon}"</li> <li><strong>L-smoothness</strong>: A smoothness condition stating that the gradient is Lipschitz continuous (possibly under non-Euclidean norms). "We begin by presenting the assumption of layer-wise $L$-smoothness."</li> <li><strong>Layer-wise learning rates</strong>: Step sizes assigned per layer, allowing different layers to update at different speeds based on their characteristics. "Layerwise adaptive learning rates~\citep{you2017scaling,you2019large} are widely used"</li> <li><strong>Linear Minimization Oracle (LMO)</strong>: An oracle that returns the minimizer of a linear function over a given feasible set; central to Frank-Wolfe-style methods. "The LMO is a fundamental concept in convex optimization"</li> <li><strong>LM head</strong>: The final output projection layer in LLMs that maps hidden states to vocabulary logits. "embedding, LM head, normalization layers."</li> <li><strong>Modular duality</strong>: A theoretical framework linking norms and optimization dynamics, informing the design of geometry-aware methods. "the theory of modular duality in optimization and the perspective of steepest descent under different operator norms"</li> <li><strong>Newton-Schulz iterations</strong>: An iterative method to approximate matrix inverse square roots or orthogonal factors, used here to compute LMO directions efficiently. "computed efficiently via Newton-Schulz iterations"</li> <li><strong>Nuclear norm</strong>: The sum of a matrix’s singular values; the dual of the operator norm in certain settings, used for dual-norm noise measurement. "with dual nuclear norm (scaled by $\sqrt{d_{\mathrm{out}/d_{\mathrm{in}$)"</li> <li><strong>Operator norm</strong>: The induced norm of a linear map between normed spaces, measuring the maximum output norm over unit input norm. "the ``$ab$" induced operator norm is defined as"</li> <li><strong>Orthogonalized updates</strong>: Update directions adjusted to enforce or exploit orthogonality structures in matrix parameters. "performing orthogonalized updates on matrix parameters."</li> <li><strong>RMS norm</strong>: A norm that scales the Euclidean norm by the inverse square root of dimension, i.e., root-mean-square magnitude. "the RMS norm is defined as"</li> <li><strong>RMS normalization</strong>: Normalization that scales a vector by its root-mean-square value to stabilize updates. "RMS normalization vectors"</li> <li><strong>Signum</strong>: An optimizer that uses the element-wise sign of momentum or gradients to form updates. "update these weight-sharing layers with Signum (see \cref{tbl:lmo})."</li> <li><strong>Singular value decomposition (SVD)</strong>: A matrix factorization into orthogonal factors and singular values, used to construct LMO directions. "Write the SVD as $W = U\Sigma V^\top$."</li> <li><strong>Stochastic gradient noise</strong>: Random fluctuations in gradient estimates due to minibatch sampling or stochasticity in data. "The stochastic gradient noise is heterogeneous across groups and layers in transformers."</li> <li><strong>Trace inner product</strong>: The matrix inner product defined by the trace of the product of one matrix transpose with another. "We use $\langle \cdot,\cdot\rangle\langle A,B\rangle = \mathrm{tr}(A^{\top}B)$"
Collections
Sign up for free to add this paper to one or more collections.