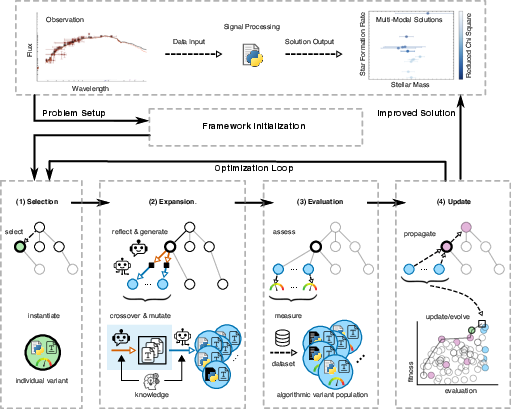
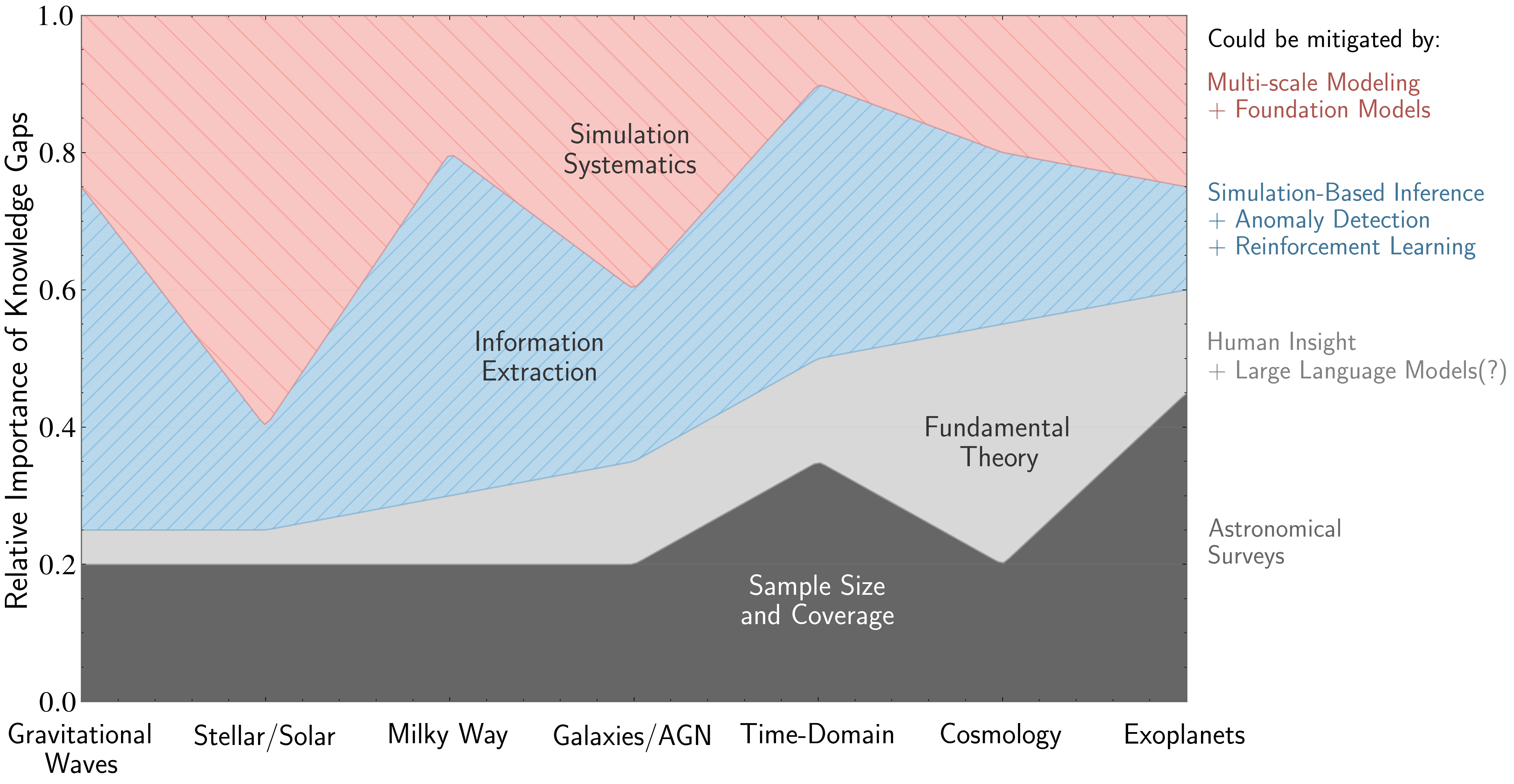
Deep Learning in Astrophysics (2510.10713v1)
Abstract: Deep learning has generated diverse perspectives in astronomy, with ongoing discussions between proponents and skeptics motivating this review. We examine how neural networks complement classical statistics, extending our data analytical toolkit for modern surveys. Astronomy offers unique opportunities through encoding physical symmetries, conservation laws, and differential equations directly into architectures, creating models that generalize beyond training data. Yet challenges persist as unlabeled observations number in billions while confirmed examples with known properties remain scarce and expensive. This review demonstrates how deep learning incorporates domain knowledge through architectural design, with built-in assumptions guiding models toward physically meaningful solutions. We evaluate where these methods offer genuine advances versus claims requiring careful scrutiny. - Neural architectures overcome trade-offs between scalability, expressivity, and data efficiency by encoding physical symmetries and conservation laws into network structure, enabling learning from limited labeled data. - Simulation-based inference and anomaly detection extract information from complex, non-Gaussian distributions where analytical likelihoods fail, enabling field-level cosmological analysis and systematic discovery of rare phenomena. - Multi-scale neural modeling bridges resolution gaps in astronomical simulations, learning effective subgrid physics from expensive high-fidelity runs to enhance large-volume calculations where direct computation remains prohibitive. - Emerging paradigms-reinforcement learning for telescope operations, foundation models learning from minimal examples, and LLM agents for research automation-show promise though are still developing in astronomical applications.
Summary
- The paper presents a formal treatment of inductive bias and physical symmetries by integrating physics-informed constraints into deep learning models for astronomical data.
- It outlines the shift from classical methods to specialized architectures like CNNs, Transformers, and GNNs, enhancing scalability, expressivity, and data efficiency.
- The review emphasizes rigorous uncertainty quantification, simulation-based inference, and the need for ecosystem development to further integrate DL in astrophysical research.
Deep Learning in Astrophysics: Methodological Advances, Domain Integration, and Future Prospects
Introduction and Context
The review "Deep Learning in Astrophysics" (2510.10713) provides a comprehensive and critical synthesis of the integration of deep learning (DL) into astronomical research. The author systematically addresses the methodological evolution from classical statistics and ML to modern neural architectures, emphasizing the unique requirements of astronomical data—scalability, generalizability, and data efficiency. The review is notable for its rigorous treatment of inductive bias, the explicit encoding of physical symmetries and conservation laws, and the careful delineation of where DL offers genuine advances versus where claims require skepticism.
Figure 1: Taxonomic hierarchy of statistical methods in astronomy, illustrating the nested relationship between statistical modeling, classical ML, and deep learning, with word sizes reflecting prevalence in the literature as of July 2025.
Methodological Foundations: From Classical ML to Physics-Informed Deep Learning
The review begins by situating DL within the broader taxonomy of statistical methods, clarifying the distinctions and overlaps between classical ML and neural network-based approaches. The author highlights the curse of dimensionality as a fundamental limitation for classical methods, which cannot simultaneously achieve scalability, expressivity, and data efficiency in high-dimensional astronomical datasets.
Figure 2: Schematic of the trade-offs between scalability, expressivity, and data efficiency for various modeling approaches; deep learning aims to achieve all three by encoding physical assumptions.
The review then details the architectural innovations that have enabled DL to overcome these trade-offs:
- Convolutional Neural Networks (CNNs): Encode translation invariance and hierarchical feature extraction, aligning with the structure of imaging data and outperforming classical wavelet-based methods for large-scale surveys.
- Recurrent Neural Networks (RNNs) and Transformers: RNNs model temporal dependencies in time series, but transformers, with their attention mechanisms, have supplanted RNNs for spectra and irregular time series by capturing long-range dependencies and global context.
- Graph Neural Networks (GNNs): Naturally represent irregular, relational data such as galaxy catalogs and merger trees, enabling message passing and permutation invariance.
Figure 3: Evolution of ML methods in astronomy from 2015 to 2025, showing the proliferation of specialized neural architectures and probabilistic methods.
The review emphasizes that the success of these architectures is contingent on the alignment of their inductive biases with the structure of astronomical data. The author provides a formal treatment of equivariance and invariance, demonstrating how physical symmetries (translation, rotation, scale, Lorentz) are encoded in network design to ensure physically meaningful generalization.
Figure 4: (A) Encoding physical symmetries via equivariant layers; (B) Physics-informed neural networks enforcing conservation laws and differential equations as constraints.
Physics-Informed Neural Networks and Simulation-Based Inference
A central theme is the integration of physical knowledge into DL models. The review details two complementary strategies:
- Architectural Encoding of Symmetries: Networks are constructed to be equivariant or invariant under relevant physical transformations, reducing the hypothesis space and improving data efficiency.
- Physics-Informed Losses: Conservation laws and differential equations are incorporated as differentiable constraints in the loss function, enabling models to generalize beyond the training distribution and respect known physics.
The review provides concrete examples, such as non-parametric recovery of the Milky Way's gravitational potential using neural networks constrained by the collisionless Boltzmann equation, and the use of physics-informed neural networks in stellar atmospheres, solar physics, and ISM chemistry.
Cross-Cutting Techniques: Multi-Scale Modeling, SBI, and Anomaly Detection
The modularity of DL components allows for the construction of specialized solutions to multi-scale and multi-modal problems:
- Multi-Scale Modeling: Encoder-decoder and U-Net architectures learn mappings between simulation resolutions, enabling "baryonification" of N-body simulations and surrogate modeling for subgrid physics. The review cautions against overinterpretation of "super-resolution" claims, noting that DL cannot create information absent in the input.
Figure 5: Deep learning for multi-scale modeling, learning mappings between simulation resolutions and acting as learned subgrid prescriptions.
- Simulation-Based Inference (SBI): The review traces the evolution from Approximate Bayesian Computation and GANs (which suffer from mode collapse and unreliable uncertainty quantification) to normalizing flows, diffusion models, and flow matching. These neural density estimators enable field-level Bayesian inference and systematic anomaly detection in high-dimensional, non-Gaussian data.
Figure 6: Neural density estimation approaches for SBI, contrasting normalizing flows (invertible transformations) and diffusion models (gradual noise corruption and denoising).
Figure 7: Schematic of neural density estimation for SBI and anomaly detection, showing the learning of joint, posterior, or likelihood distributions from simulation-observation pairs.
- Anomaly Detection: Variational autoencoders and density estimators are used for systematic outlier identification in large surveys, with applications ranging from spectroscopic anomaly detection to real-time transient triage in time-domain astronomy.
Foundation Models, Reinforcement Learning, and Agentic Research
The review critically examines the promise and limitations of foundation models in astronomy. While self-supervised and cross-modal pretraining can improve performance in label-scarce regimes, the review notes that supervised methods remain optimal when sufficient labeled data is available. The author distinguishes between architectural choices and true foundation model capabilities (zero/few-shot transfer), cautioning against terminological inflation.
Figure 8: Foundation models leverage self-supervised pretraining for strong performance with minimal labeled data, enabling rapid adaptation to new tasks.
Reinforcement learning is highlighted as a tool for optimizing operational workflows (e.g., telescope scheduling, adaptive optics, detector control), with demonstrated improvements over heuristic methods in complex, dynamic environments.
The review also discusses the nascent field of agentic research, where LLMs and agentic frameworks are used for semi-autonomous scientific discovery, hypothesis generation, and workflow automation. The author notes the current limitations of LLMs in perception and scientific coding, emphasizing the need for ecosystem development and rigorous benchmarking.
Figure 9: Agentic research framework for autonomous scientific discovery, with agents iteratively generating, evaluating, and refining hypotheses.
Implications, Limitations, and Future Directions
The review provides a nuanced assessment of where DL is likely to have the greatest impact in astronomy, identifying information extraction and simulation systematics as the most addressable bottlenecks. The author presents a domain-by-domain analysis, mapping the relative importance of sample size, theory, information extraction, and simulation systematics.
Figure 10: Knowledge gaps across astronomical domains, with hatching indicating gaps potentially mitigated by deep learning.
The review concludes with a set of summary points and future issues, emphasizing the need for:
- Data-efficient DL methods leveraging physical priors and self-supervision.
- Expanded incorporation of physical symmetries and conservation laws.
- Rigorous blind testing and uncertainty quantification for SBI.
- Development of true foundation models with demonstrated transfer capabilities.
- Ecosystem and educational development to integrate DL as an extension of statistical methods.
Conclusion
"Deep Learning in Astrophysics" offers a rigorous, technically detailed, and balanced synthesis of the state of DL in astronomy. The review's primary contributions are its formal treatment of inductive bias and physical symmetries, its critical assessment of methodological advances, and its clear articulation of the limitations and open challenges. The implications for both practical applications and theoretical understanding are substantial: DL is positioned as a powerful extension to the astronomical toolkit, particularly for high-dimensional, non-Gaussian, and simulation-limited problems. However, the review cautions against overreliance on DL in the absence of physical understanding, rigorous validation, and careful uncertainty quantification. The future of DL in astronomy will depend on continued methodological innovation, domain-specific integration, and a balanced approach to both skepticism and enthusiasm.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Deep Learning in Astrophysics — Explained Simply
Overview
This paper is a guide to how deep learning (a kind of artificial intelligence that uses neural networks) is changing astronomy. Modern telescopes create enormous amounts of data—far more than humans can look through by hand. The paper explains how deep learning can help astronomers find patterns, discover rare events, and learn about the universe, while also warning where we need to be careful so we don’t fool ourselves.
What questions does the paper ask?
The review focuses on a few big questions that matter to astronomers:
- What can deep learning really do better than older, “classical” methods?
- How can we teach AI about the rules of physics so it learns faster and makes more trustworthy predictions?
- Where has deep learning already helped in astronomy (like finding rare objects or improving simulations), and where is it still unproven?
How does the paper approach this?
This is a review paper, which means the author read and organized many research studies to explain what works, what doesn’t, and why. It also maps how different AI methods have spread through astronomy over time, and it explains the core ideas behind major neural network designs using plain-language examples.
Here are the main ideas and tools, explained with simple analogies:
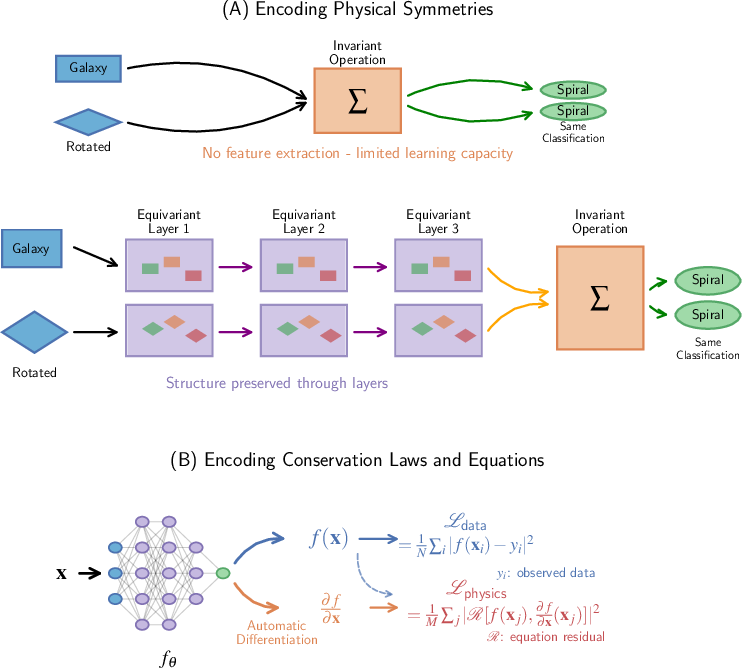
- Inductive bias: This means “built-in assumptions.” Just like you might guess a ball will fall because you know gravity, we can build rules into AI models so they prefer answers that match physics (like symmetry and conservation laws). This helps AI learn well even with limited examples.
- Convolutional Neural Networks (CNNs): Think of a small window sliding over an image to spot edges or shapes. CNNs are great for pictures of the sky because the same feature (like a galaxy spiral arm) can appear anywhere in the image.
- Recurrent Neural Networks (RNNs): These are for sequences, like light that changes over time. They keep a kind of “memory” of what came before. They’re useful, but newer methods are often better for very long or messy time series.
- Transformers and attention: Instead of reading a sequence step-by-step, transformers let every part “look at” every other part directly. That’s perfect for things like star spectra (rainbow-like fingerprints), where important signals for the same element can appear far apart in wavelength. Attention means the model learns what to focus on—like listening closely to certain instruments in an orchestra.
- Graph Neural Networks (GNNs): Space isn’t a neat grid—it’s a web of galaxies connected by gravity. GNNs treat objects (like galaxies) as dots (nodes) and their relationships (like distance or interactions) as lines (edges). They’re powerful for learning from irregular, real-world structures, such as galaxy clusters or merger trees.
- Simulation-based inference: Sometimes we can simulate the universe forward (like a video game with physics), but we can’t write a simple formula to go backwards from data to causes. These methods use lots of simulations plus neural networks to figure out which physical settings best explain the observations.
- Anomaly detection: This is about teaching AI what “normal” looks like so it can flag the weird stuff—like fast radio bursts or odd transients—that might be new discoveries.
- Multi-scale modeling: The universe has action at many sizes at once—from tiny star-forming regions to entire galaxies. Neural networks can learn “shortcuts” for small-scale physics from expensive, detailed simulations and plug them into big, cheaper simulations to save time while keeping accuracy.
What did the paper find, and why does it matter?
The review highlights several important conclusions:
- No single method wins at everything. Classical methods are fast and need fewer examples but struggle with very complex patterns. Plain neural networks are flexible and scalable but can be data-hungry.
- The big unlock is building physics into the AI. When networks respect symmetries and conservation laws, they become more data-efficient, more stable, and better at generalizing to new situations—not just memorizing the training set.
- Choice of architecture should match the data:
- Images → CNNs shine.
- Spectra and long sequences → Transformers work best because they capture long-range relationships.
- Irregular structures (like galaxy maps or merger histories) → GNNs are a strong fit.
- Deep learning enables new kinds of science:
- Simulation-based inference lets astronomers analyze complex data where old statistical formulas break down.
- Anomaly detection helps find rare, surprising events that can lead to breakthroughs.
- Multi-scale modeling improves large simulations by learning from a few very detailed ones.
- Adoption is rising, but caution is needed. Deep learning now appears in a significant fraction of astronomy papers and is catching up with classical machine learning. Still, the field must handle common pitfalls:
- Domain shift: Models trained on one kind of data (like simulations) may fail on another (real telescope data).
- Scarce labels: We have billions of measurements but far fewer confirmed examples to train on.
- Reliability: We need uncertainty estimates and physical sanity checks, not just high accuracy numbers.
- New frontiers are promising but early:
- Reinforcement learning for smarter telescope scheduling and operations.
- Foundation models that can learn from fewer examples by pretraining on huge datasets.
- AI assistants (LLMs) to help automate parts of research, with careful human oversight.
What’s the impact for the future?
If used wisely, deep learning can make astronomy faster and more powerful:
- It can sort through massive surveys to find important patterns and rare objects quickly.
- It can connect theory and data by baking physics into the model design.
- It can improve simulations used to test ideas about the universe.
- It can help us measure uncertainties and avoid being misled by noise or bias.
But the paper stresses balance: pair AI with physics, validate carefully, and be transparent about what models can and cannot do. With that approach, deep learning becomes a dependable partner for discovery—not a black box.
Knowledge Gaps
Knowledge Gaps, Limitations, and Open Questions
Below is a focused list of what remains missing, uncertain, or unexplored in the paper, articulated to enable actionable follow-up research:
- Lack of standardized, domain-shift-aware benchmarks comparing deep learning to classical methods across core astronomical modalities (images, spectra, irregular time series, point catalogs), with agreed metrics for scalability, generalization, data efficiency, and calibration quality.
- No quantitative evidence or case studies demonstrating when encoding specific physical symmetries (e.g., rotational, scale, permutation invariance) measurably improves out-of-distribution performance on real survey data; need controlled ablation studies and cross-instrument validation.
- Unclear best practices for enforcing conservation laws and differential equations in neural architectures (e.g., physics-informed neural networks): how to balance hard vs soft constraints, manage stiffness, boundary/initial conditions, and noisy inputs while preserving numerical stability.
- Insufficient guidance on uncertainty quantification: how to achieve calibrated predictive distributions (e.g., posterior coverage, simulation-based calibration) under observational systematics, selection effects, and non-Gaussian noise typical of modern surveys.
- No rigorous framework for sim-to-real transfer: how to mitigate mismatch between simulations and observations (baryonic physics, feedback models, instrument systematics) while preserving sensitivity to genuine anomalies; need principled domain adaptation protocols and error budgets.
- Missing methodology for handling label scarcity at scale beyond architecture design: active learning policies for spectroscopic follow-up, weak/self-supervised objectives tailored to astrophysical data, and strategies to leverage noisy/partial labels without biasing inference.
- Interpretability is not operationalized: methods to link learned features (e.g., attention heads, GNN messages) to physically meaningful structures (atomic transitions, tidal fields, merger histories), with validation protocols (counterfactuals, mechanistic probes) that avoid post hoc speculation.
- Anomaly detection lacks reproducible criteria: how to control false positives, the look-elsewhere effect, and prioritize follow-up efficiently; need standardized novelty metrics, cross-survey replication procedures, and human-in-the-loop triage designs.
- Transformer use for spectra and time series leaves open questions about physically grounded positional encodings (phase-aware, Doppler-shift-aware), handling irregular sampling and gaps, and robustness to instrument-dependent wavelength calibration and resolution changes.
- Attention mechanisms for spectra are not tied to atomic/molecular knowledge: how to incorporate line lists, radiative transfer constraints, and blending physics into attention structure to improve fidelity and interpretability across varying conditions (temperature, gravity, metallicity).
- Graph construction for GNNs is under-specified: criteria for edge definitions (proximity, tidal fields, causal links), sensitivity to graph topology/hyperparameters, and scalability to billion-node catalogs; need comparisons to traditional statistics (e.g., two-point functions) under controlled settings.
- Open question on multi-scale modeling: how to learn subgrid closures from high-fidelity simulations that remain stable, conservative, and generalize across cosmologies/feedback prescriptions; require verification on extrapolative regimes and long-horizon error accumulation studies.
- No clear pathway for combining simulation-based inference with deep architectures while retaining Bayesian rigor: protocols for likelihood-free inference with realistic systematics, posterior diagnostics, and end-to-end uncertainty propagation from raw data to parameters.
- Robustness to domain shift is asserted but not demonstrated: require empirical stress tests across instruments, epochs, observing conditions, and selection functions, including adversarial and rare-event scenarios representative of survey operations (e.g., LSST, Euclid).
- Scalability at survey scale is discussed conceptually but lacks engineering guidance: memory/computation footprints, distributed training/inference, model compression/distillation/quantization, and edge deployment on observatory pipelines with strict latency constraints.
- Missing evaluation under realistic noise models: systematic tests with correlated backgrounds, cosmic rays, PSF variability, calibration drift, and blended sources that reflect operational pipelines, not idealized datasets.
- No treatment of rigorous causal inference: how to distinguish correlational patterns learned by networks from causal relationships relevant to physical interpretation and decision-making (e.g., intervention on telescope scheduling, follow-up triggers).
- Reinforcement learning for telescope operations remains speculative: need simulators with high-fidelity constraints, multi-objective reward design (scientific yield, safety, resource use), sim-to-real transfer strategies, and risk assessment for live deployment.
- Foundation models for astronomy are not concretized: pretraining corpora composition (multi-modal imaging/spectra/time series), self-supervised objectives aligned with physical tasks, data governance, compute budgets, and environmental impacts; require community benchmarks for few-shot transfer.
- LLM agents for research automation lack reliability protocols: provenance tracking, reproducibility guarantees, hallucination mitigation, audit trails for scientific claims, and integration with domain-specific tooling and data repositories.
- Ethical and sustainability considerations are absent: carbon footprint of large-scale training, equitable access to compute, and guidelines for responsible deployment within public observatory infrastructures.
- Taxonomy and adoption analyses rely on LLM-derived literature graphs without methodological transparency: need reproducible pipelines, bias assessments (e.g., keyword drift, summary quality), error analyses, and open datasets to validate the reported trends.
- Theoretical links (e.g., infinite-width networks to Gaussian Processes, scattering transform) are not translated into actionable design rules for finite, practical models in astronomy; require recipes for kernel choices, invariance targets, and performance guarantees.
- No standardized reporting for deep learning studies in astronomy: recommended checklists for dataset curation, train/test splits under domain shift, uncertainty calibration, interpretability evidence, release of code/models, and documentation of negative results.
- Incomplete guidance on architecture selection and hybridization: decision frameworks for choosing CNNs, transformers, GNNs, or hybrids based on data modality, physics priors, and operational constraints, with comparative ablations and failure mode catalogs.
- Follow-up resource optimization is not addressed: integrating active learning with observatory scheduling (spectroscopic time, space-based follow-up), cost-aware target selection, and closed-loop learning with real-time data streams.
Practical Applications
Immediate Applications
Below are applications that can be deployed with current methods and infrastructure, leveraging the paper’s findings on architectures with inductive biases, simulation-based inference, anomaly detection, and emerging agentic tooling.
- CNN/U-Net image cleanup and source segmentation for survey pipelines (academia, observatories, software)
- Use: Real-time artifact removal, background subtraction, deblending, and pixel-level segmentation for instruments like Rubin/LSST, Euclid, HST/JWST archival reprocessing.
- Tools/workflows: U-Net–based QA modules inserted before source extraction; learned PSF/sky models; auto-generated masks for cosmic rays/satellite trails.
- Assumptions/dependencies: Representative labeled frames, calibration data (bias/dark/flat), stable instrument systematics; routine re-training after hardware/config changes.
- Morphology and structural parameter estimation with CNNs (academia, observatories)
- Use: Automated galaxy morphology classification, bar/bulge/disk decomposition, tidal feature detection.
- Tools/workflows: CNNs fine-tuned on survey-specific imagery; uncertainty-calibrated outputs integrated with catalog builders.
- Assumptions/dependencies: Domain adaptation across seeing, depth, filters; human-in-the-loop vetting for rare classes; robust uncertainty estimates.
- Transformer-based spectroscopic analysis for stellar and galaxy properties (academia; spectroscopy in materials/chemistry as a cross-sector analog)
- Use: Estimation of stellar labels (Teff, log g, [Fe/H], abundances), galaxy redshifts and line diagnostics by attending across widely separated wavelengths.
- Tools/workflows: Attention models replacing or augmenting template fitting in SDSS/DESI pipeline stages; calibrated posteriors via ensembles or Bayesian layers.
- Assumptions/dependencies: High-quality labeled spectra for pretraining; careful continuum normalization; domain shift mitigation across instruments and S/N.
- Time-domain event triage with RNNs/Transformers (academia, observatories)
- Use: Early alert classification of transients/variables to prioritize follow-up; adaptive prioritization as more data arrives.
- Tools/workflows: Streaming models deployed in alert brokers; confidence- and cost-aware ranking for ToO scheduling.
- Assumptions/dependencies: Low-latency inference infrastructure; label drift monitoring; calibration across cadence gaps and seasonal systematics.
- Simulation-based inference (SBI) with normalizing flows for cosmological parameters (academia, HPC)
- Use: Likelihood-free, field-level inference when analytic likelihoods fail (non-Gaussian fields, complex systematics).
- Tools/workflows: nflows/sbi-based pipelines; amortized posteriors trained on suites of simulations; plug-ins to existing MCMC workflows for priors and diagnostics.
- Assumptions/dependencies: High-fidelity simulation suites spanning plausible parameter ranges; simulator–data mismatch modeling; posterior coverage validation.
- GNNs for intrinsic alignments, environment effects, and cosmology from discrete catalogs (academia)
- Use: Predict/mitigate weak-lensing systematics; learn environment-conditioned properties; infer cosmological parameters directly from galaxy point sets.
- Tools/workflows: Message-passing GNNs on kNN/Delaunay graphs; PointNet-like models for permutation-invariant sets; feature attribution for physical interpretability.
- Assumptions/dependencies: Reliable graph construction (edges, distances, selection effects); robust cross-validation on mocks/held-out skies.
- Anomaly and outlier detection with autoencoders/VAEs (academia, observatories, policy/planetary defense)
- Use: Discovery of rare transients, odd spectra, artifacts indicating novel phenomena or threats (e.g., atypical NEO trails).
- Tools/workflows: Unsupervised embeddings; reconstruction-error thresholds; human-in-the-loop vetting queues integrated with alert streams.
- Assumptions/dependencies: Tight false-positive control; continuous recalibration to evolving data; feedback loops for active learning.
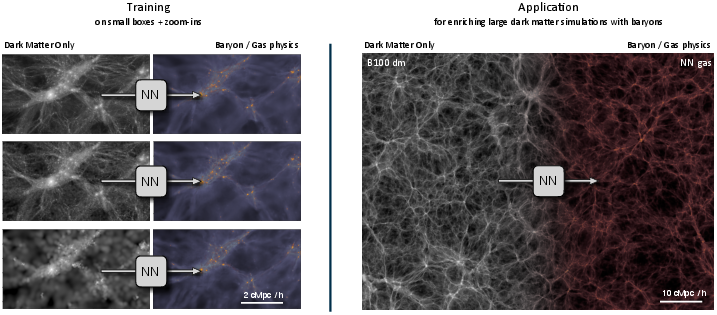
- Learned surrogates for subgrid physics to accelerate large-volume simulations (academia, HPC; cross-sector: climate/CFD in energy, aerospace)
- Use: Emulators that learn from high-fidelity zoom-ins to speed up cosmological hydrodynamics or radiative transfer in large boxes.
- Tools/workflows: U-Net/ResNet surrogates trained on paired high/low-resolution runs; uncertainty-aware emulation; hybrid physics-ML loops.
- Assumptions/dependencies: Coverage of training regimes; conservation/physics constraints; rigorous generalization and error-bounding tests.
- RL-assisted telescope scheduling and operations (observatories, robotics/software)
- Use: Weather-aware scheduling, dynamic cadence optimization, target prioritization under resource constraints.
- Tools/workflows: RL policies trained in realistic simulators; safety filters; multi-objective reward design (science yield, fairness, uptime).
- Assumptions/dependencies: High-fidelity simulators; guardrails and operator oversight; continuous off-policy evaluation.
- LLM-based research assistants for literature, code scaffolding, and metadata (academia, education, software)
- Use: Rapid literature mapping, data pipeline boilerplate generation, documentation and provenance capture.
- Tools/workflows: Domain-adapted LLMs with retrieval-augmented generation; notebook templates; auto-generated experiment cards.
- Assumptions/dependencies: Human review; citation grounding; reproducibility policies; restricted-model deployment where data are proprietary.
- Cross-sector immediate transfers of methods
- Remote sensing and Earth observation: CNN/U-Net image cleanup and segmentation; GNNs on geospatial point clouds. Dependencies: sensor-specific calibration.
- Industrial and energy time series: Transformer forecasting/anomaly detection for predictive maintenance and grid stability. Dependencies: robust backtesting, drift monitoring.
- Materials/chemistry spectroscopy: Attention models for Raman/IR/NMR peak attribution and quantification. Dependencies: curated spectral libraries.
Long-Term Applications
These opportunities require further research, scaling, or ecosystem development (e.g., data sharing, compute, validation frameworks), but are strongly motivated by the review’s emphasis on inductive biases, physics constraints, and scalable probabilistic inference.
- Physics-informed neural networks with hard conservation/geometry constraints for robust cross-instrument generalization (academia, engineering, robotics)
- Vision: Architectures that provably respect symmetries and conservation laws, reducing data requirements and improving extrapolation to new regimes.
- Dependencies: Stable training with constraints, certified uncertainty, benchmarks spanning domain shifts.
- Foundation models for astronomy (multi-modal, multi-instrument) enabling few-shot adaptation (academia, software)
- Vision: Pretrained models over images, spectra, and time series that provide universal embeddings and toolkits for downstream tasks (classification, regression, anomaly detection) with minimal labels.
- Products: “AstroFM” APIs; embedding services for brokers; cross-survey self-supervised pretraining hubs.
- Dependencies: Cross-institution data-sharing agreements, standardized data schemas, exabyte-scale compute, evaluation suites for bias and calibration.
- End-to-end autonomous observatories (observatories, robotics/policy)
- Vision: RL/agentic systems that plan observations, configure instruments, manage adaptive optics, and trigger follow-ups with explicit safety and fairness constraints.
- Dependencies: High-fidelity digital twins; formal verification; governance for risk, accountability, and equitable time allocation.
- Survey-scale field-level cosmology via SBI (academia, HPC)
- Vision: Likelihood-free inference that ingests maps/catalogs at pixel/object level across multiple probes to deliver joint posteriors at scale.
- Dependencies: Scalable normalizing flows, bias-aware simulators, selection-function modeling, end-to-end posterior validation and coverage guarantees.
- Planetary-defense–grade anomaly detection across federated sky surveys (policy, observatories)
- Vision: Cross-survey, low-latency anomaly network for unusual moving objects or impactors with prioritized alerting and explainable evidence.
- Dependencies: Interoperable alert formats, robust cross-matching, false-alarm governance, international response protocols.
- Multi-scale surrogate cascades for exascale “simulation-in-the-loop” experiment design (academia, energy/climate/aerospace)
- Vision: Hierarchies of learned emulators that couple microphysics to large-scale simulations, enabling rapid design-space exploration and adaptive experimental campaigns.
- Dependencies: Trusted error bounds, active learning loops, standardized interfaces between solvers and surrogates.
- Agentic LLMs for closed-loop scientific workflows (academia, software, education)
- Vision: Agents that propose hypotheses, design simulations/observations, run pipelines, and draft analyses with provenance and reproducibility baked in.
- Dependencies: Tool-use sandboxes, audit trails, dataset/model registries, community benchmarks for correctness and novelty.
- Uncertainty-aware ML standards for mission planning and policy (policy, standards bodies)
- Vision: Adopted practices for calibration, coverage testing, shift-robustness, and interpretability that inform funding, mission risk assessments, and public communication.
- Dependencies: Shared metrics, open testbeds, independent validation, regulatory guidance.
- Citizen science co-pilots and inquiry-driven education (daily life, education)
- Vision: ML assistants that surface likely-rare events to volunteers, explain model rationales, and turn real survey data into interactive learning modules.
- Dependencies: Accessible data portals, pedagogical framing, safeguards against overconfidence and bias.
Common assumptions and dependencies across applications
- Domain shift and simulator mismatch: Requires domain adaptation, nuisance-parameter modeling, and continuous validation.
- Data scarcity of labels: Emphasizes self/few-shot learning, active learning, and human-in-the-loop verification.
- Compute and tooling: GPU/TPU access, MLOps for versioning and reproducibility, and observability for data/model drift.
- Uncertainty and interpretability: Probabilistic predictions, calibration checks, and physics-informed constraints are essential for scientific and policy-grade use.
- Governance and ethics: Data rights, transparency, bias auditing, and clear human oversight are mandatory, especially for autonomous or policy-relevant systems.
Glossary
- Acoustic glitches: Abrupt features in stellar oscillation spectra caused by sharp structural transitions within stars. "revealing deep stellar structure through acoustic glitches and mixed modes"
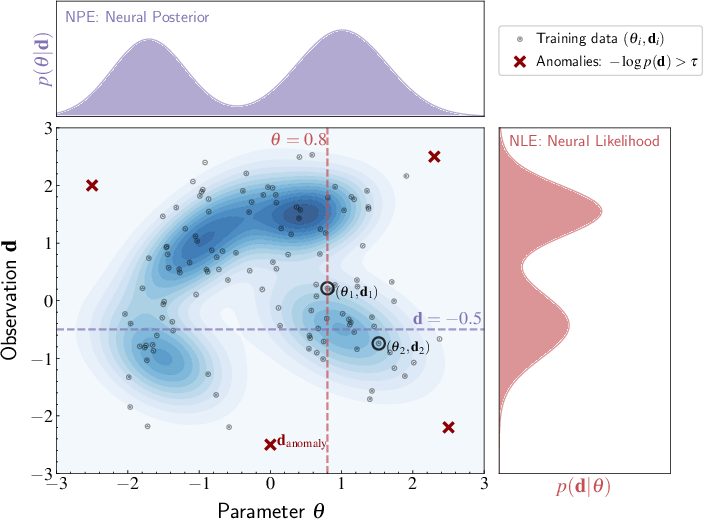
- Anomaly detection: Techniques to identify rare or unusual data instances that deviate from expected patterns. "Simulation-based inference and anomaly detection extract information from complex, non-Gaussian distributions where analytical likelihoods fail, enabling field-level cosmological analysis and systematic discovery of rare phenomena."
- Attention mechanism: A neural operation that learns pairwise relationships across inputs to focus computation on the most relevant parts. "Transformer architectures are built on the attention mechanismâa mechanism that computes relationships between all pairs of inputs simultaneously, which we detail below."
- Asteroseismology: The paper of stellar interiors by analyzing oscillation modes in their brightness or spectra. "asteroseismology evolved from fitting individual oscillation frequencies to globally characterizing entire power spectra, revealing deep stellar structure through acoustic glitches and mixed modes \citep{Garcia2019}."
- Bias-variance dilemma: The trade-off between underfitting due to overly simple models (bias) and overfitting due to overly flexible models (variance). "Critics articulated what appeared to be a fundamental barrier: the bias-variance dilemma \citep{Geman1992}."
- Conservation laws: Fundamental physical invariants (e.g., energy, momentum) used as constraints in model design. "Neural architectures overcome trade-offs between scalability, expressivity, and data efficiency by encoding physical symmetries and conservation laws into network structure, enabling learning from limited labeled data."
- Convolution theorem: A Fourier analysis principle linking convolution in the spatial domain to multiplication in the frequency domain. "The mathematical foundation comes from the convolution theoremâspatial translations become phase shifts that leave Fourier magnitudes unchanged."
- Cross-correlation: A similarity measure over shifts used to align or compare signals, such as spectra or time series. "Cross-correlation measures radial velocities by comparing observed and template spectra at all wavelength shifts \citep{Simkin1974}"
- Curse of Dimensionality: The exponential growth in data and computation required as dimensionality increases. "The root of these trade-offs lies in the curse of dimensionality."
- Deformation stability: Representation robustness where small input distortions yield small changes in feature space. "Beyond translation invariance, this architecture provides deformation stabilityâsmall input distortions produce only small representation changes."
- Domain shift: Systematic differences between training and deployment data distributions that challenge generalization. "True generalizability requires robustness to domain shiftsâsystematic differences between training and application contexts, such as models trained on simulations encountering real observationsâwhile maintaining sensitivity to genuine anomalies that could represent new physics."
- Fast Blue Optical Transients: A class of extremely luminous, rapidly evolving optical transients with blue spectra. "time-domain surveys identified Fast Blue Optical Transients like AT 2018cow \citep{Prentice2018}"
- Fast Radio Bursts (FRBs): Millisecond-duration radio flashes of extragalactic origin with unknown progenitors. "Fast Radio Burstsâmillisecond pulses fitting no known categoryâ emerged from big data analysis \citep{Lorimer2007}."
- Field-level cosmological analysis: Inference performed directly on cosmological fields (e.g., density or shear maps) rather than summary statistics. "enabling field-level cosmological analysis and systematic discovery of rare phenomena."
- Friends-of-friends algorithm: A clustering method that links points within a threshold distance to identify groups. "The friends-of-friends algorithm groups galaxies by linking those within a threshold distanceâessentially finding connected components in a proximity graph \citep{Turner1976}."
- Gaussian Processes (GPs): Nonparametric Bayesian models defining distributions over functions with kernel-based covariance. "Gaussian Processes offer exquisite expressivity with principled uncertainty quantification but become computationally intractable for large datasets \citep{Rasmussen2006}."
- Graph Neural Networks (GNNs): Neural architectures operating on graphs via learned message passing over nodes and edges. "Graph neural networks explicitly model such data by representing objects as nodes and relationships as edges \citep{Scarselli2009}."
- Inductive bias: Built-in assumptions guiding learning toward preferred solutions beyond consistency with observed data. "These networks incorporate inductive biasesâbuilt-in assumptions guiding learning toward physically meaningful solutions."
- Intrinsic alignments: Correlated galaxy shape orientations arising from local tidal fields, a major systematic in weak lensing. "For galaxy intrinsic alignmentsâa key systematic in weak lensingâ\citet{Craigie2025b} showed GNNs learn alignments from local galaxy environments"
- Kennicutt–Schmidt relation: Empirical relation linking gas surface density to star formation rate in galaxies. "and the Kennicutt-Schmidt relation linking gas surface density to star formation rate \citep{Kennicutt1998}."
- Matched filtering: Optimal signal detection by correlating data against template waveforms under known noise models. "Matched filtering in gravitational wave detection compares strain data against templates at all time lags \citep{Owen1999}."
- Merger trees: Hierarchical graphs describing the assembly history of dark matter halos or galaxies. "Similarly, dark matter halos form merger trees encoding assembly history."
- Mexican hat wavelet: The second derivative of a Gaussian used for blob and point-source detection in images. "Mexican hat wavelets (the second derivative of a Gaussian) for identifying blob-like structures and point sources \citep{Starck1998}."
- Multi-head attention: Parallel attention mechanisms that learn complementary relationships and features. "Multi-head attention further extends this mechanism by running parallel attention operations (heads), each with its own set of weight matrices:"
- Multi-scale neural modeling: Neural approaches that connect and learn across disparate spatial or temporal scales. "Multi-scale neural modeling bridges resolution gaps in astronomical simulations, learning effective subgrid physics from expensive high-fidelity runs to enhance large-volume calculations where direct computation remains prohibitive."
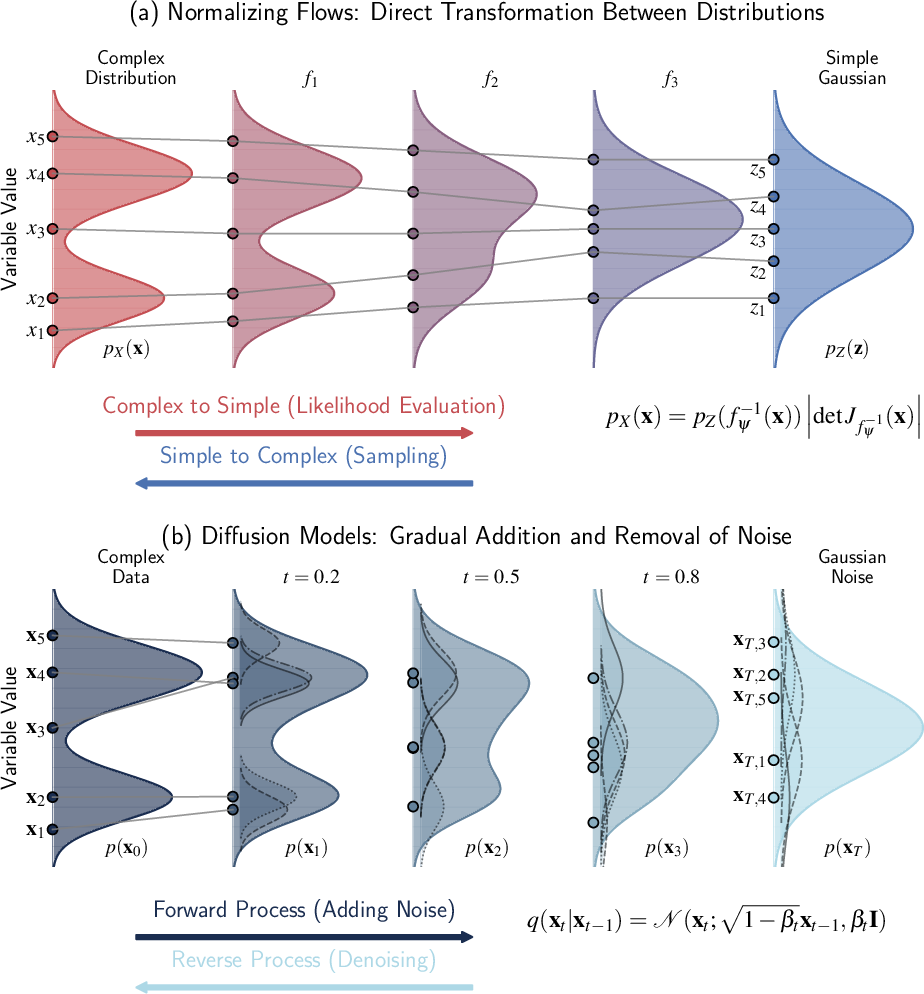
- Normalizing flows: Invertible neural density estimators enabling flexible likelihoods for probabilistic inference. "powered by normalizing flows \citep{JiminezRezende2015} which provide the neural density estimation framework (Section \ref{subsubsection:normalizing-flows})."
- Permutation invariance: Model outputs that are invariant to the ordering of input elements (e.g., nodes). "The aggregation operator (sum, mean, or max) ensures permutation invariance---reordering neighbors does not change the result, just as the mean mass of galaxies does not depend on their catalog order."
- Photometric redshift: Redshift estimated from broadband photometry rather than spectroscopy. "Related methods use local galaxy density for photometric redshift estimation, though without explicit graph construction \citep{Menard2013}."
- Physics-informed neural networks: Neural models that incorporate physical laws or constraints directly into architectures or losses. "deep learning, inductive bias, physical symmetries, physics-informed neural networks, multi-scale modeling, simulation-based inference, anomaly detection, foundation models, reinforcement learning, LLMs, astronomical surveys"
- Physical symmetries: Invariances (e.g., translation, rotation) encoded in model design to improve generalization. "Neural architectures overcome trade-offs between scalability, expressivity, and data efficiency by encoding physical symmetries and conservation laws into network structure, enabling learning from limited labeled data."
- Primordial non-Gaussianity: Deviations from Gaussian statistics in initial conditions of the early universe. "to probe primordial non-Gaussianity and nonlinear structure formation \citep{Bernardeau2002}."
- Residual connections: Skip connections that add inputs to outputs to improve gradient flow in deep networks. "This concept later inspired ``residual connections''in CNNs \citep{He2016}, enabling training of networks hundreds of layers deep."
- Scattering transform: A cascade of wavelet convolutions and nonlinearities providing stability and invariances for signal representations. "This hierarchical structure has theoretical foundations in the scattering transform \citep{Bruna2012, Mallat2011}, a mathematical framework that helped researchers understand why CNNs succeed."
- Sérsic functions: Parametric models for galaxy surface brightness profiles characterized by a Sérsic index. "When modeling galaxy profiles with Sérsic functions or spectral lines with Voigt profiles, we constrain our search to particular mathematical families based on physical reasoning."
- Simulation-based inference (SBI): Likelihood-free Bayesian inference that leverages simulations to learn posteriors or likelihoods. "Simulation-based inference \citep[see] []{Cranmer2020a} enables rigorous Bayesian inference matching our statistical traditions while scaling to modern data volumes (Section \ref{subsection:simulation-based-inference})"
- Subgrid physics: Effective modeling of unresolved processes in coarse simulations using information from high-resolution runs. "learning effective subgrid physics from expensive high-fidelity runs to enhance large-volume calculations where direct computation remains prohibitive."
- Transformer architectures: Attention-centric neural models that capture long-range dependencies without recurrent processing. "Transformer architectures \citep{Vaswani2017} have grown since 2022, excelling at capturing long-range dependencies in irregular time series through attention mechanisms (Section \ref{subsubsection:transformer-architectures})."
- Two-point correlation functions: Statistics describing spatial clustering via pairwise correlations, central in cosmology. "Classical approaches focus on dominant statistical features like two-point correlation functions capturing Gaussian fluctuations \citep{Peebles1980}."
- U-Net: An encoder–decoder convolutional architecture for dense predictions like segmentation and denoising. "Around 2018, U-Net \citep{Ronneberger2015} enabled pixel-level predictions for artifact removal \citep[e.g.,] []{Zhang2020} and source segmentation \citep[e.g.,] []{Hausen2020}."
- Universal Approximation Theorem: Theoretical result that sufficiently wide feedforward networks can approximate any continuous function. "the universal approximation theorem guarantees that feedforward networks can approximate any continuous function to arbitrary accuracy given sufficient neurons \citep{Cybenko1989,Hornik1989}."
- Variational Autoencoders (VAEs): Generative models that learn latent representations via variational inference. "Autoencoders and Variational Autoencoders \citep[VAEs;] []{Kingma2013} emerged as alternatives to traditional dimensionality reduction like PCA \citep{Baldi1989}."
- Voigt profiles: Spectral line shapes formed by convolving Gaussian and Lorentzian components. "When modeling galaxy profiles with Sérsic functions or spectral lines with Voigt profiles, we constrain our search to particular mathematical families based on physical reasoning."
- Weak lensing: Subtle gravitational distortion of background galaxy shapes by intervening mass distributions. "a key systematic in weak lensing"
Collections
Sign up for free to add this paper to one or more collections.