Papers
Topics
Authors
Recent
Assistant
AI Research Assistant
Well-researched responses based on relevant abstracts and paper content.
Custom Instructions Pro
Preferences or requirements that you'd like Emergent Mind to consider when generating responses.
Gemini 2.5 Flash
Gemini 2.5 Flash 134 tok/s
Gemini 2.5 Pro 41 tok/s Pro
GPT-5 Medium 27 tok/s Pro
GPT-5 High 29 tok/s Pro
GPT-4o 119 tok/s Pro
Kimi K2 180 tok/s Pro
GPT OSS 120B 418 tok/s Pro
Claude Sonnet 4.5 37 tok/s Pro
2000 character limit reached

Lectures on entanglement, von Neumann algebras, and emergence of spacetime (2510.07017v1)

Published 8 Oct 2025 in hep-th

Abstract: We review recent developments in the use of von Neumann algebras to analyze the entanglement structure of quantum gravity and the emergence of spacetime in the semi-classical limit. Von Neumann algebras provide a natural framework for describing quantum subsystems when standard tensor factorizations are unavailable, capturing both kinematic and dynamical aspects of entanglement. The first part of the review introduces the fundamentals of von Neumann algebras, including their classification, and explains how they can be applied to characterize entanglement. Topics covered include modular and half-sided modular flows and their role in the emergence of time, as well as the crossed-product construction of von Neumann algebras. The second part turns to applications in quantum gravity, including an algebraic formulation of AdS/CFT in the large-$N$ limit, the emergence of bulk spacetime structure through subregion-subalgebra duality, and an operator-algebraic perspective on gravitational entropy. It also discusses simple operator-algebraic models of quantum gravity, which provide concrete settings in which to explore these ideas. In addition, several original conceptual contributions are presented, including a diagnostic of firewalls and an algebraic formulation of entanglement islands. The review concludes with some speculative remarks on the mathematical structures underlying quantum gravity.

Summary

  • The paper introduces a von Neumann algebra framework to analyze infinite entanglement in quantum gravity and demonstrates how modular theory leads to an emergent notion of time.
  • The paper systematically classifies von Neumann factors (Types I, II, III) to capture distinct entanglement structures and establishes the subregion-subalgebra duality linking bulk regions and boundary observables.
  • The paper reformulates entanglement wedge reconstruction as an algebraic problem, providing insights into quantum error correction and the role of additivity anomalies in holographic duality.

Operator Algebraic Approaches to Entanglement and the Emergence of Spacetime

Overview and Motivation

This work provides a comprehensive review of the application of von Neumann algebra theory to the analysis of entanglement structure in quantum gravity, with a particular focus on the emergence of spacetime in the semiclassical limit. The central thesis is that von Neumann algebras offer a natural and powerful language for describing quantum subsystems in contexts where Hilbert space factorization fails, such as quantum field theory (QFT) and holographic dualities. The review systematically develops the operator-algebraic framework, elucidates its classification, and demonstrates its utility in both kinematic and dynamical aspects of entanglement, culminating in a detailed algebraic formulation of AdS/CFT and the subregion-subalgebra duality.

Von Neumann Algebras and Entanglement Structure

The paper begins by motivating the need for a generalized notion of subsystems in quantum many-body systems and QFT, where infinite entanglement and gauge constraints preclude Hilbert space factorization. The operator-algebraic approach replaces the subsystem notion with von Neumann subalgebras, capturing all physically accessible operations. The classification of von Neumann factors (Type I, II, III) is shown to correspond to broad classes of entanglement structure:

  • Type I: Admits Hilbert space factorization; standard quantum information tools apply.
  • Type II: No minimal projections; allows for a continuous dimension function; all states are infinitely entangled.
  • Type III: All projections are infinite; no trace exists; modular theory is required for entanglement characterization.

The emergence of Type III1_1 algebras in local QFT is attributed to the infinite short-range entanglement at region boundaries, while the large-NN limit in holographic CFTs leads to infinite long-range entanglement, also resulting in Type III1_1 structure.

Modular Theory and Emergent Time

A central technical tool is Tomita-Takesaki modular theory, which provides a canonical modular flow and modular conjugation for any von Neumann algebra with a cyclic and separating vector. The modular flow generates an emergent notion of time and encodes the entanglement spectrum, generalizing the entanglement Hamiltonian to the operator-algebraic setting. For Type III algebras, modular flows are outer automorphisms, and the spectrum of the modular operator provides a fine-grained invariant (Connes' SS-invariant) for further classification (Type IIIλ_\lambda, Type III1_1, etc.).

Subregion-Subalgebra Duality and Bulk Emergence

The operator-algebraic formulation of AdS/CFT is developed by identifying the large-NN limit of the boundary CFT with a generalized free field theory, where the operator algebras associated with boundary regions become Type III1_1 in the continuum. The subregion-subalgebra duality posits a one-to-one correspondence between causally complete bulk subregions and emergent von Neumann subalgebras of the boundary CFT. This duality is illustrated in (Figure 1): Figure 1

Figure 1: (a) Subregion-subalgebra duality: bulk subregions OiO_i correspond to boundary subalgebras Ai\mathcal{A}_i, with geometric and causal relations mapped to algebraic inclusions and commutants. (b) Causal diamonds in the bulk not touching the boundary correspond to emergent subalgebras without geometric boundary interpretation.

This duality reformulates entanglement wedge and causal wedge reconstruction in algebraic terms, allowing for the precise identification of bulk regions (including those not anchored to the boundary) with specific boundary subalgebras. The emergent causal structure and locality in the bulk are encoded in the commutant structure and inclusion relations among these algebras.

Algebraic Formulation of Entanglement Wedge Reconstruction

The entanglement wedge reconstruction is recast as an algebraic statement: the von Neumann algebra generated by single-trace operators in a boundary region AA (denoted YA^\mathcal{Y}_{\hat{A}}) is identified with the bulk algebra of the causal wedge, while the full entanglement wedge algebra XA\mathcal{X}_A is generated by modular flow of these operators. The inclusion YA^⊂XA\mathcal{Y}_{\hat{A}} \subset \mathcal{X}_A is generically proper, reflecting the superadditivity of entanglement wedges and the nonlocal generation of boundary subalgebras in the large-NN limit. This is visualized in (Figure 2) and (Figure 3): Figure 2

Figure 2: The RT surface γA\gamma_A and the bulk dual subregion bA\mathfrak{b}_A of a boundary region AA; the entanglement wedge is the domain of dependence of bA\mathfrak{b}_A.

Figure 3

Figure 3: Infinite long-range entanglement between AA and its complement in the large-NN limit manifests as infinite short-range entanglement near the RT surface in the bulk.

The algebraic approach also provides a natural definition of entanglement islands and a diagnostic for firewalls: the existence of operators in the large-NN limit outside the single-trace algebra is necessary for a smooth geometric extension behind the horizon; otherwise, a firewall is present.

Additivity Anomaly and Quantum Error Correction

A key result is the additivity anomaly: in the large-NN limit, the boundary subalgebras associated with unions of regions are generically superadditive, in contrast to the additivity property at finite NN. This anomaly underlies the quantum error-correcting properties of holographic codes and the redundancy of bulk information encoding. The superadditivity is illustrated in (Figure 4) and (Figure 5): Figure 4

Figure 4: Superadditivity of entanglement wedges: the entanglement wedge of A1∪A2A_1 \cup A_2 is strictly larger than the union of the individual wedges.

Figure 5

Figure 5: For two intervals A1,A2A_1, A_2, the algebra generated by their union is strictly larger than the union of the individual algebras, as shown by the region bounded by the curves t=±x2+a2−b2t = \pm \sqrt{x^2 + a^2 - b^2}.

This structure is essential for the boundary realization of bulk quantum error correction and the emergence of entanglement islands.

Applications to Black Hole Physics and Generalized Entropies

The operator-algebraic framework is applied to the analysis of black hole interiors, firewalls, and the algebraic formulation of entanglement islands. The crossed-product construction is introduced as a method to obtain a Type II algebra from a Type III algebra by adjoining the modular group, providing a setting for defining generalized gravitational entropies in the absence of Hilbert space factorization.

Implications and Future Directions

The review demonstrates that operator algebras, and in particular the subregion-subalgebra duality, provide a unifying language for the emergence of spacetime, the encoding of bulk locality and causality, and the quantum information-theoretic properties of holographic duality. The algebraic approach clarifies the role of infinite entanglement in the large-NN limit, the necessity of Type III1_1 structure for local QFT, and the mathematical underpinnings of quantum error correction in gravity.

The implications are both practical and conceptual: the framework enables precise diagnostics of bulk reconstruction, firewalls, and islands, and suggests that operator algebras will play a central role in any nonperturbative formulation of quantum gravity, especially at finite GNG_N where geometric notions break down. The algebraic perspective also opens avenues for the construction of new models of quantum gravity, the paper of diffeomorphism-invariant observables, and the exploration of the mathematical structure underlying holography.

Conclusion

This work establishes von Neumann algebra theory as an indispensable tool for the analysis of entanglement and the emergence of spacetime in quantum gravity. The operator-algebraic approach not only generalizes and refines the understanding of subsystems and entanglement in QFT and holography, but also provides a rigorous foundation for the paper of bulk reconstruction, quantum error correction, and the algebraic structure of gravitational entropy. The subregion-subalgebra duality, modular theory, and the classification of von Neumann factors together form a robust framework for future developments in the mathematical physics of quantum gravity.

File Document Download Save Streamline Icon: https://streamlinehq.com PDF File Document Download Save Streamline Icon: https://streamlinehq.com Markdown
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Explain it Like I'm 14

Overview

This paper is a set of lectures that explain how a certain kind of mathematics—called von Neumann algebras—can be used to understand quantum entanglement when the usual tools break down, and how spacetime itself might “emerge” from entanglement in the context of quantum gravity. It focuses on the AdS/CFT duality (a major idea in modern physics), where a gravity theory in a curved space is linked to a quantum theory on its boundary. The paper shows that operator algebras give a natural way to describe subsystems and their entanglement, even when the system is too “infinitely tangled” to split cleanly into parts. It then uses these ideas to explain how regions, time, and causality in spacetime can appear from the entanglement structure of the boundary theory in a certain limit.

Key Questions

The paper asks simple but deep questions:

  • If we start from a complete quantum theory of gravity with no built-in geometry, how do familiar spacetime features (like regions, time, and cause-and-effect) arise in a limit where gravity becomes weak?
  • What happens to entanglement in quantum systems with infinitely many tiny degrees of freedom, where standard ways of “cutting” the system into parts no longer work?
  • Can we describe subsystems without splitting the big Hilbert space into two pieces, and still talk about entanglement in a meaningful way?
  • In AdS/CFT, how exactly does the bulk spacetime region relate to operations in the boundary theory?
  • Can these algebraic tools explain puzzles like black hole entropy, “entanglement islands,” and whether firewalls exist?

Approach and Methods (with everyday analogies)

The paper’s approach is to switch perspectives—from “splitting the system into parts” to “listing what you can do to it.”

  • Instead of carving a system into two clean halves (which fails when entanglement is infinite), define a subsystem by a set of allowed operations—the buttons on your control panel. This set is a von Neumann algebra: it’s closed under combining operations, taking adjoints (undoing), and taking limits of sequences of operations (so it’s complete in a way that matters for physics).
  • The “complement” of a subsystem is the set of operations that don’t interfere with it (they commute). This captures the idea of independent, non-interacting parts but without needing a clean split of the Hilbert space.
  • Von Neumann algebras come in types (I, II, III). These types reflect different “entanglement behaviors.” For example:
    • Type I is the familiar case where you can split the Hilbert space and use usual quantum information tools.
    • Type III (especially type III1_1) appears in realistic quantum field theories, where there is infinite entanglement near boundaries (like an infinite number of tiny “Velcro” connections along a cut).
  • Modular theory is introduced. Think of it as a built-in, state-dependent “clock” for the algebra—a way time can “emerge” from the entanglement structure and the operations you can perform. Half-sided modular flows are special one-way time evolutions that further structure what you can do.
  • A crossed product construction lets you turn a type III algebra into something more like type II for certain purposes, helping define and compute generalized entropies relevant to gravity.
  • The paper sets up an algebraic version of AdS/CFT in the large-NN limit (where NN counts how many field degrees of freedom). In this limit, entanglement changes dramatically, and specific boundary algebras correspond to bulk spacetime subregions.

To make the need for this approach clear, the paper gives simple examples where splitting fails:

  • Lattice gauge theories: Gauge constraints tie things together so tightly that a clean split isn’t possible.
  • Infinitely many entangled spin pairs: If every pair across a cut is entangled and you have infinitely many, then “un-entangling” would cost infinite energy—so no clean split.
  • Relativistic quantum field theories: There’s infinite short-range entanglement at any cut; entanglement entropy diverges (grows like the boundary area divided by a tiny cutoff), so usual tools don’t apply directly.

Main Findings and Why They Matter

  • Subregion–subalgebra duality: Every causally complete region in the bulk spacetime is matched to a specific kind of emergent von Neumann subalgebra on the boundary. Bulk geometric relations (like one region being inside another, or two regions being spacelike separated) translate into algebraic relations (like one algebra being a subset of another, or two algebras commuting).
    • This is powerful: it means spacetime structure—locality, causality, and even notions of time—can be encoded by the algebra of operations available in the boundary theory.
  • Type III1_1 algebras are key: In the large-NN limit (which corresponds to weak gravity), the boundary subalgebras that match bulk local regions are of type III1_1. This reflects the system’s infinite long-range entanglement and explains why usual “split the Hilbert space” methods fail but the algebraic approach succeeds.
  • Modular flows give emergent time: The state and algebra naturally come with a special flow—like a built-in clock—helping define and organize dynamics even when a usual time variable is not obvious.
  • Algebraic reconstruction of the bulk: The paper reformulates entanglement wedge and causal wedge reconstruction—ways to recover bulk information from boundary data—entirely in terms of operator algebras. This works for very general subregions and clarifies how error-correcting properties arise.
  • Gravitational entropy and islands: Using crossed products and operator-algebraic models, the paper gives an algebraic perspective on generalized gravitational entropies (including those of black holes and de Sitter space) and formulates “entanglement islands” in purely algebraic terms. “Islands” are surprising extra regions that count toward entropy calculations and help explain the Page curve in black hole evaporation.
  • Conceptual contributions: The lectures include a diagnostic for firewalls (whether the inside of a black hole is smooth or “burns”), and present simple algebraic models that illustrate horizons and the emergence of causal structure in cosmology.

These results matter because they replace fragile, regulator-dependent calculations with a framework that directly captures the “infinite entanglement” reality of quantum field theories and holography. They show spacetime can be viewed as a “geometrization” of certain abstract algebras that emerge from the boundary theory.

Implications and Impact

  • A new foundation for quantum gravity: The work suggests that operator algebras are the right language not only in the weak-gravity limit but also when gravity is fully quantum and classical geometry disappears. This offers clues to the true mathematical structure of quantum gravity.
  • Entanglement as the backbone of spacetime: It strengthens the idea that how parts of a quantum system are entangled literally builds the spacetime they live in. Locality and causality in the bulk are encoded by commutation relations and inclusion relations between boundary algebras.
  • Practical advantages: It avoids relying on cutoffs and regulators that can hide key physics, and it unifies many ideas (like error correction, islands, and modular time) under one algebraic roof.
  • Broader reach: The same tools also connect to energy conditions in QFT (ANEC, QNEC), toy models of holography, and the paper of observables in low-dimensional gravity theories, indicating wide applicability.

In short, the paper shows how to think about “parts” of a quantum system when those parts cannot be separated in the usual way, and how that new viewpoint naturally leads to spacetime emerging from entanglement in holographic theories. It offers a clear, sturdy mathematical framework—based on von Neumann algebras—that ties together many puzzles in modern physics.

Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Knowledge Gaps

Knowledge gaps, limitations, and open questions

The paper advances an operator‑algebraic framework for entanglement and spacetime emergence in AdS/CFT, but several issues remain unresolved. Future researchers could target the following concrete gaps:

  • Formal proof and scope of subregion–subalgebra duality:
    • Provide a general, rigorous derivation that any causally complete bulk subregion corresponds to a unique emergent type III1_1 boundary subalgebra in the large‑NN limit, including regions without boundary geometric support (e.g., interior causal diamonds).
    • Establish necessary and sufficient conditions (on states, dynamics, and $1/N$ expansion) for duality to hold and characterize its uniqueness up to algebraic isomorphisms and state‑dependent equivalences.
    • Quantify stability of the duality under $1/N$ corrections: what algebraic deformations (centers, type changes, approximate commutation) appear at finite GNG_N?
  • Explicit constructions and checks in concrete CFTs:
    • Construct boundary von Neumann subalgebras for specific bulk regions using explicit CFT operator families (free fields, large‑NN gauge theories, integrable models) and verify commutant relations that mirror bulk spacelike separation.
    • Compute modular automorphism groups of these subalgebras and show they reproduce bulk geometric flows (where applicable).
  • Type transitions and entanglement structure:
    • Derive precise criteria (beyond heuristics) for the transition from type I to type III1_1 algebras in the large‑NN limit, including quantifying how long‑range entanglement divergences lead to type III1_1 structure.
    • Identify model‑independent diagnostics to distinguish short‑range vs. long‑range contributions driving non‑factorization (e.g., operational tests based on relative entropies or modular inclusions).
  • Finite‑GNG_N (finite‑NN) regime:
    • Develop the operator‑algebraic description when geometry is “fuzzy”: what replaces sharp type III1_1 subalgebras, and how are locality and causality encoded algebraically at finite GNG_N?
    • Define and analyze approximate subregion–subalgebra duality (e.g., in terms of approximate commutants or almost‑inclusions) and quantify errors with $1/N$.
  • Modular and half‑sided modular flows as emergent time:
    • Demonstrate conditions under which modular/half‑sided modular flows correspond to physical bulk time evolutions and identify when they do not (e.g., state‑dependent vs. geometric flow).
    • Compute modular Hamiltonians for nontrivial holographic states beyond vacuum/excited states with symmetry and compare with bulk generators (including interactions and dressing).
  • Crossed‑product constructions and generalized entropies:
    • Provide a direct, non‑perturbative derivation of RT/QES formulae from crossed‑product extensions (e.g., type III1_1 → type II1_1 with a trace) in interacting theories, and clarify the uniqueness of the extension used to define a gravitational “trace.”
    • Map operator‑algebraic entropy definitions to replica‑wormhole path integrals and identify where they agree or diverge, including in time‑dependent or non‑AdS setups.
  • Islands and firewalls in algebraic terms:
    • Supply operational criteria (invariants, modular inclusions, centers, or relative commutants) that predict island formation and firewall presence, and test them in dynamical black hole formation/evaporation models.
    • Connect algebraic diagnostics to semiclassical QES computations, including thresholds for transitions between phases (no‑island/island, smooth horizon/firewall).
  • Gauge constraints and edge modes:
    • Develop a unified operator‑algebraic treatment of lattice/continuum gauge theories that reconciles Gauss‑law‑induced centers and edge modes with type III1_1 locality, and clarify how this interacts with holographic subregion duality.
  • Quantum error correction with type III1_1 algebras:
    • Characterize code properties (distance, correctable subalgebras, noise models) when logical algebras are type III1_1 and quantify approximate QEC performance at finite NN.
    • Construct explicit holographic codes implementing subregion–subalgebra duality (including non‑boundary‑anchored regions) and analyze robustness to interactions/backreaction.
  • Observables and diffeomorphism invariance:
    • Give a systematic boundary construction of diffeomorphism‑invariant bulk operators and their algebras (including gravitational dressing) and determine how dressing choices modify the boundary algebra type and commutants.
  • Causal and event horizons in the stringy regime:
    • Provide computable operator‑algebraic recipes for defining and locating bulk horizons (causal/event) without relying on semiclassical geometry, and validate them in solvable models.
  • Extension beyond AdS:
    • Generalize the operator‑algebraic framework to flat space and de Sitter beyond toy models: identify dual boundary‑like structures (if any), define subregion algebras, and formulate generalized entropy without AdS asymptotics.
  • Boundary interpretation of bulk volume and complexity:
    • Identify algebraic quantities (e.g., spectral invariants, modular data, or traces in crossed products) that robustly correlate with bulk volume/complexity and determine the conditions under which such relations hold.
  • Handling unbounded operators and non‑separable Hilbert spaces:
    • Extend the analysis beyond bounded operators to include essential unbounded field operators using rigorous domains or affiliated operators, and address non‑separability issues in thermodynamic/continuum limits via GNS representations.
  • State spaces and thermal/KMS structure:
    • Systematically treat normal vs. non‑normal states, KMS states, and their modular data in holographic contexts, including consequences for emergent time and entanglement measures.
  • Quantitative links to ANEC/QNEC and chaos:
    • Develop operator‑algebraic derivations that tie modular theory and subregion algebras to energy conditions (ANEC/QNEC) and chaotic diagnostics, and test them across holographic and non‑holographic models.
  • Rigor vs. heuristics:
    • Replace heuristic arguments (e.g., “infinite energy barrier” for factorization failure) with precise mathematical criteria and proofs, and catalogue known counterexamples with conditions preventing them in holographic CFTs.
  • Universality and exceptions:
    • Determine classes of CFTs (matter content, interactions, symmetry) for which the emergent type III1_1 structure and duality hold, identify exceptions, and specify minimal hypotheses required for the framework to apply.
  • Computational tools and benchmarks:
    • Develop practical computational methods (analytic/numeric) for constructing emergent algebras, modular flows, and crossed‑product traces in realistic large‑NN theories, and benchmark against known semiclassical results.
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Practical Applications

Immediate Applications

The following items describe applications that can be deployed now or prototyped with existing tools, grounded in the paper’s methods (von Neumann algebras, modular theory, half-sided modular flows, crossed-product constructions) and its operator-algebraic formulation of AdS/CFT.

  • Academia (high-energy theory and quantum information)
    • Actionable use: Replace Hilbert-space factorization with von Neumann subalgebras to analyze entanglement in quantum field theories and large-N CFTs where factorization fails. Adopt commutant structure and type III₁ local algebras to paper subregion physics, energy conditions, and causal relations.
    • Tools/workflows: Define local algebras, compute commutants for spacelike separation, use modular theory to construct modular Hamiltonians and emergent time, use crossed products to introduce traces and handle generalized entropies; reformulate entanglement wedge/causal wedge reconstruction algebraically via subregion-subalgebra duality.
    • Assumptions/dependencies: Continuum/QFT limit (infinite entanglement), type III₁ algebras for local regions, existence of faithful normal states, need for regulators in numerics; large-N (G_N → 0) regime when interpreting boundary/bulk dualities.
  • Academia (mathematical physics)
    • Actionable use: Treat “classification of von Neumann algebras” as a “classification of entanglement types,” enabling systematic diagnostics of entanglement structures—including modular and half-sided modular flows as probes of emergent time and fine entanglement features.
    • Tools/workflows: Use spectral projections, commutants, and modular automorphism groups; employ crossed-product constructions to connect type III₁ algebras to tracial settings for entropy-like quantities.
    • Assumptions/dependencies: Operator-algebraic expertise; careful control of domains of modular operators; availability of physically meaningful states/weights.
  • Software (research tooling and reproducibility)
    • Actionable use: Develop open-source numerical libraries to approximate modular flows, compute commutants, simulate crossed-product algebras, and perform algebraic bulk reconstruction on lattice-regulated models.
    • Potential products: “Operator Algebra Toolbox” (Python/Julia) for modular Hamiltonians and half-sided modular flows; “Subregion–Subalgebra Mapper” for entanglement wedge/causal wedge numerics; “Crossed-Product Entropy Lab” to prototype generalized entropy calculations.
    • Assumptions/dependencies: Discretization (lattice/finite N) for type III approximations; HPC resources for large operator spaces; validation against known analytic results.
  • Quantum computing industry (quantum error correction and subsystem codes)
    • Actionable use: Design and analyze subsystem codes inspired by subregion-subalgebra duality—logical operators (bulk) encoded in boundary subalgebras with correctable erasures reflecting holographic quantum error-correcting properties (e.g., islands as code-theoretic features).
    • Tools/workflows: Algebraic subsystem code synthesis using commutants and conditional expectations; noise modeling with operator-algebraic channels; benchmarking emergent locality/causality in code spaces.
    • Assumptions/dependencies: Finite-dimensional approximations (type I) of type III structures; mapping abstract algebras to hardware-native operator sets; realistic noise and syndrome extraction on current devices.
  • Academia (energy conditions and QFT inequalities)
    • Actionable use: Apply modular theory and operator algebras to rigorously formulate and prove ANEC/QNEC in QFT with improved clarity around assumptions and domain issues.
    • Tools/workflows: Use half-sided modular inclusions and modular flow to derive energy inequalities; extend to curved spacetimes and holographic contexts.
    • Assumptions/dependencies: Well-defined local algebras and states; technical control over modular operators; continuity with existing algebraic QFT frameworks.
  • Education (graduate-level training and curricula)
    • Actionable use: Introduce operator-algebraic subsystems, modular theory, and subregion-subalgebra duality in advanced courses; supervise computational labs that implement modular flow numerics and algebraic reconstruction.
    • Tools/workflows: Lecture notes and problem sets on von Neumann algebras and holography; small-scale coding projects using the above-mentioned libraries.
    • Assumptions/dependencies: Faculty expertise across math/physics/CS; modest compute resources; alignment with research goals.
  • Policy (research programs and community infrastructure)
    • Actionable use: Fund cross-disciplinary centers and reproducible software efforts connecting operator algebras, quantum information, and quantum gravity; establish shared benchmarks for algebraic reconstruction and entropy calculations.
    • Tools/workflows: Community repositories, data/model sharing, and training workshops bridging mathematics and physics.
    • Assumptions/dependencies: Sustained funding and collaboration; open licensing and maintenance plans.

Long-Term Applications

The following items require further research, scaling, or development—often beyond the large-N limit—before they can be broadly deployed or translated into technology.

  • Academia (quantum gravity foundations)
    • Application: Use subregion-subalgebra duality to define bulk spacetime non-perturbatively at finite G_N, with operator algebras replacing classical geometry as fundamental. Develop algebraic formulations of horizons, islands, and firewall diagnostics beyond semiclassical limits.
    • Potential outputs: New formulations of quantum gravity; rigorous definitions of locality, causality, and entropy in the full quantum regime.
    • Dependencies: Advances in operator-algebraic techniques for finite G_N; reconciliation with experimental/observational constraints; deeper understanding of type III structures and states at strong coupling.
  • Software (general-purpose operator-algebra simulation platforms)
    • Application: Build scalable platforms that automatically compute commutants, modular automorphism groups, half-sided inclusions, and crossed products for realistic field-theoretic and holographic models.
    • Potential products: “Modular Flow Analyzer” for emergent-time simulations; “Algebraic Bulk Reconstruction Engine” for large-scale holographic inference; integrated visualization tools for causal structures from commutants.
    • Dependencies: Algorithmic breakthroughs (e.g., efficient representations of infinite-dimensional algebras), robust numerics for continuum limits, substantial HPC capabilities.
  • Quantum computing industry (holographically inspired architectures)
    • Application: Engineer “holographic” quantum processors whose robustness emerges from code subalgebras mirroring bulk–boundary duality; use operator algebras to schedule logical operations via modular flows and to model complex noise with algebraic channels.
    • Potential products/workflows: Compilers that optimize logical locality via commutant relations; resource estimation frameworks based on crossed-product “entropy accounting.”
    • Dependencies: Scalable fault-tolerant hardware; tools to bridge infinite-dimensional theory to finite device primitives; demonstrated performance gains over standard QEC frameworks.
  • Experimental physics (analog gravity and entanglement structure)
    • Application: Use operator-algebraic insights to design analog experiments probing emergent causal structures, modular flows, and entropy-like quantities in condensed matter or quantum simulators (e.g., cold atoms, photonics).
    • Potential outputs: Experimental proxies for horizons, islands, and modular dynamics; validation of algebraic reconstruction principles.
    • Dependencies: Feasible mappings from type III features to controllable finite systems; high-fidelity measurement and control to resolve modular effects.
  • Theoretical cosmology and energy constraints
    • Application: Extend algebraic proofs of ANEC/QNEC and related inequalities to cosmological settings, informing bounds on energy densities and the viability of exotic spacetimes.
    • Potential outputs: Model-independent constraints for early-universe and horizon physics; cross-checks on semiclassical gravity assumptions.
    • Dependencies: Integration with observational cosmology; rigorous handling of curved backgrounds in algebraic QFT.
  • Education and workforce development
    • Application: Establish long-term training pipelines combining operator algebras, quantum information, and gravity; standardize curricula and shared computational resources.
    • Potential outputs: A community of researchers fluent in algebraic QFT and holography with strong computational literacy.
    • Dependencies: Institutional commitment, sustained funding, and accessible tooling.

Notes on Assumptions and Dependencies (cross-cutting)

  • Large-N/semiclassical limit: Many immediate applications (especially holographic ones) rely on the G_N → 0 (N → ∞) regime; extending to finite G_N is a long-term goal.
  • Type III₁ local algebras: Core to QFT locality and to the paper’s duality; practical implementations often require lattice or finite-dimensional approximations.
  • Faithful normal states: Needed for modular theory and many operator-algebraic constructions; care is required to ensure physical relevance.
  • Regulators and discretization: Numerical and experimental instantiations typically depend on lattice cutoffs, posing nontrivial convergence and validation challenges.
  • Mathematical expertise and HPC: Widespread adoption depends on training and computational infrastructure to handle noncommutative operator algebras at scale.
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Glossary

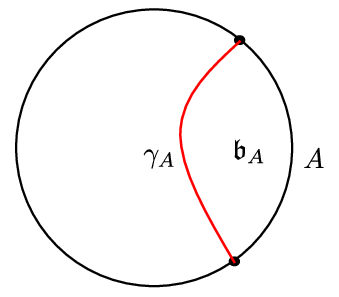
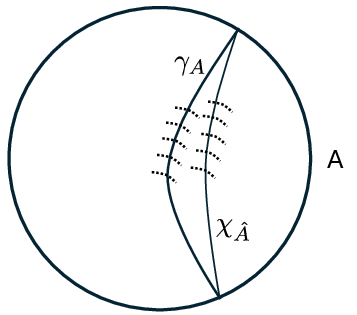
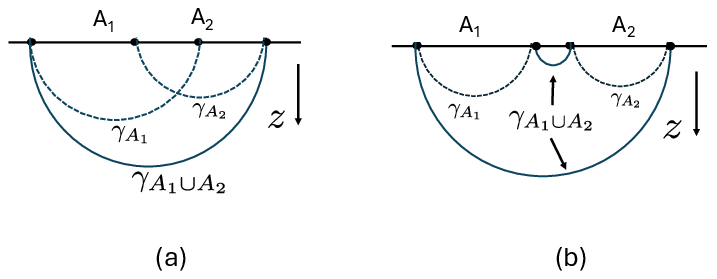
  • AdS/CFT duality: A conjectured equivalence between quantum gravity in asymptotically anti–de Sitter (AdS) spacetime and a conformal field theory (CFT) living on its boundary. "In the context of the AdS/CFT duality~\cite{Mal97,GubKle98,Wit98}, the Ryu-Takayanagi proposal~\cite{RyuTak06,RyuTak06-2,HubRan07,Wal11,EngWal14,LewMal13,FauLew13} strongly indicates that in a quantum gravitational system the spacetime structure is tied to the entanglement structure of the system."
  • algebraic QFT: An operator-algebraic formulation of quantum field theory focusing on algebras of observables associated with spacetime regions. "Operator algebras have long been used to characterize relativistic quantum field theory, an approach known as algebraic QFT (see e.g.~\cite{Haa92,Ara99,Bor00,Yng04,HolWal08,HolWal14,Yng14,Wit18,Wit21a} for textbooks and reviews)"
  • Average Null Energy Condition (ANEC): A constraint stating that the integral of the null energy density along complete null geodesics is nonnegative. "algebraic formulations and proofs of the Average Null Energy Condition (ANEC)~\cite{CasTes17,FauLei16}"
  • C* algebra: A norm-closed, involutive (∗) algebra of bounded operators satisfying the C*-identity, used as a general framework for operator algebras. "such an algebra is called a {\bf C∗C^* algebra}."
  • causal complement: The set of spacetime points that are spacelike separated from a given set. "A prime on a region YY denotes its causal complement (with the bulk or boundary context understood)"
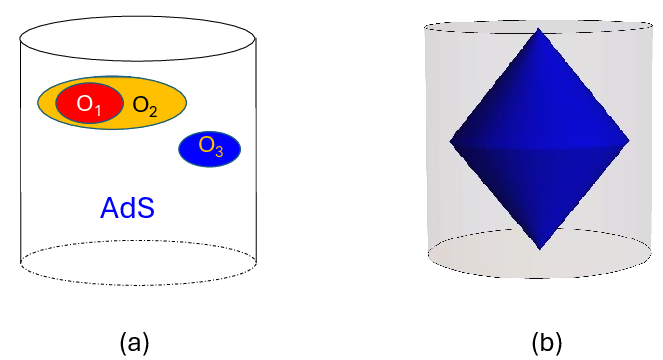
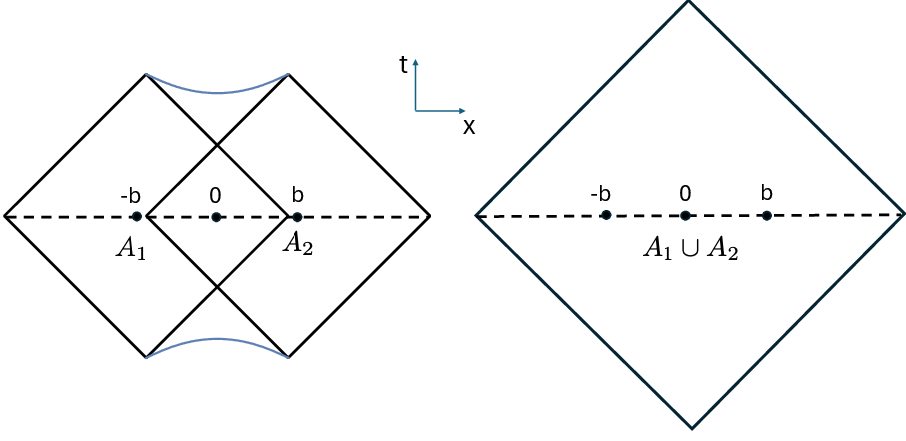
  • causal diamond: The intersection of the causal future of a point with the causal past of another, forming a diamond-shaped spacetime region. "(b) A causal diamond in the global AdS that does not touch the boundary is dual to an emergent subalgebra in the boundary system that does not have a geometric description."
  • causal wedge reconstruction: The procedure of reconstructing bulk operators from boundary data associated with the causal wedge of a region. "and causal wedge reconstruction~\cite{BanDou98,Ben99,BalKraLaw98,HamKab05,HamKab06,KabLif11,Hee12,HeeMar12,PapRaj12,Mor14,Hub14,EngPen21a,Wit23,EngLiu25}"
  • Cauchy slice: A spacelike hypersurface intersecting every inextendible causal curve exactly once, providing initial data for evolution. "Suppose RR is a subregion of a Cauchy slice."
  • center (of a von Neumann algebra): The subalgebra of elements commuting with every element of the algebra; trivial center characterizes factors. "The center of $\sZ (\sM)$ of a von Neumann algebra $\sM$ is defined as the collection of elements of $\sM$ that commute with $\sM$"
  • commutant: The set of bounded operators that commute with every operator in a given set or algebra. "We define the {\bf complement} of a subsystem---specified by a von Neumann algebra $\sM$---in terms of its commutant $\sM'$"
  • crossed-product construction: An operator-algebraic construction that builds a larger von Neumann algebra from a given one and a group action (e.g., modular automorphisms). "the crossed-product construction of von Neumann algebras."
  • diffeomorphism invariant observables: Observables unchanged under smooth coordinate transformations, crucial in generally covariant theories like gravity. "constructing new models of quantum gravity and diffeomorphism invariant observables~\cite{Wit21b,ChaLon22,Wit23b,KolLiu24,AliJef23,KliLei23,KliLei23a,AliChe24a,AliChe24,AliKli24,Gom22,Gom23,Gom23a,Gom23c,Fio23,MerTap25}"
  • domain of dependence: The spacetime region uniquely determined by initial data on a subset of a Cauchy slice. "Its complement on the slice is denoted by Rˉ\bar{R}, and its domain of dependence by R^\hat{R}."
  • entanglement islands: Bulk regions that must be included in computing the entanglement entropy of boundary subregions in gravitational settings. "an algebraic formulation of entanglement islands."
  • entanglement wedge reconstruction: The recovery of bulk operators from boundary data associated with the entanglement wedge of a boundary region. "reformulates entanglement wedge reconstruction~\cite{Van09,CzeKar12,CzeKar12b,Wal12,HeaHub14,AlmDon14,JafSuh14,PasYos15,JafLew15,DonHar16,Har16,FauLew17,CotHay17} and causal wedge reconstruction"
  • factor (primary): A von Neumann algebra with trivial center; equivalently, one whose center consists only of scalars. "A von Neumann algebra is called {\bf primary} or {\bf a factor} if it has a trivial center"
  • faithful state: A state for which only the zero operator has zero expectation in the positive quadratic form sense. "A state $\om$ is {\bf faithful}, if $\om(A^\da A ) = 0$ implies that A=0A=0."
  • firewalls: Hypothetical high-energy barriers at black hole horizons arising in some resolutions of the information paradox. "including a diagnostic of firewalls"
  • Gelfand duality: The duality between commutative C*-algebras and compact Hausdorff spaces, linking algebras of functions to topological spaces. "The Gelfand duality, for instance, asserts that the algebra of continuous functions on a topological space can be employed as a description of the space itself."
  • generalized gravitational entropies: Entropy formulas in gravity that include quantum and geometric contributions beyond the classical area term. "the physical origin of generalized gravitational entropies"
  • half-sided modular flows: One-sided modular automorphism flows (e.g., defined for t ≥ 0) that generate powerful structural results in operator algebras and QFT. "We also discuss half-sided modular flows, a powerful structure that leads to another notion of emergent time."
  • Hilbert space factorization: The decomposition of a Hilbert space into a tensor product of subsystems; often absent in QFT or infinite-entanglement regimes. "The emergent entanglement structures in the N→∞N \to \infty limit cannot be captured by the standard formulation of entanglement, which defines subsystems through Hilbert space factorization."
  • Jackiw–Teitelboim gravity (JT gravity): A two-dimensional dilaton gravity model widely used as a solvable laboratory for quantum gravity. "low-dimensional quantum gravity theories such as Jackiw-Teitelboim gravity~\cite{Tei83,Jackiw,AlmPol14}"
  • large-N limit: The limit where the number of degrees of freedom N becomes large, corresponding to the semi-classical gravity limit in AdS/CFT. "an algebraic formulation of AdS/CFT in the large-NN limit"
  • modular theory: Tomita–Takesaki theory describing the modular operator and modular automorphisms associated to a von Neumann algebra and a state. "We introduce modular theory, a powerful framework for understanding entanglement in type III von Neumann algebras."
  • normal state: A state continuous in the weak operator topology, equivalently representable by a density operator on the Hilbert space. "A {\bf normal} state is defined as a state $\om$ satisfying the condition"
  • noncommutative geometries: Geometric frameworks where spaces are encoded by noncommutative operator algebras rather than commutative function algebras. "defining noncommutative geometries using noncommutative algebras (see e.g.~\cite{Con95})."
  • projection-valued measure: A measure assigning projections to measurable sets, used in the spectral theorem for self-adjoint operators. "where $\ka \in \sig (\sO)$ and $d E_\sO (\ka)$ is a projection-valued measure."
  • Quantum Null Energy Condition (QNEC): A quantum inequality relating null energy to changes in entanglement entropy along null directions. "and the Quantum Null Energy Condition (QNEC)~\cite{BalFau17,CeyFau18,FauLi18,HolLon25}."
  • relative entropy: A measure of distinguishability between two quantum states, generalizing the Kullback–Leibler divergence. "and the relative entropy between two such reduced density operators ρR\rho_R and $\sig_R$"
  • Ryu–Takayanagi proposal: The holographic formula equating boundary entanglement entropy to the area of a minimal (extremal) surface in the AdS bulk. "the Ryu-Takayanagi proposal~\cite{RyuTak06,RyuTak06-2,HubRan07,Wal11,EngWal14,LewMal13,FauLew13}"
  • semi-classical limit: The regime where quantum gravitational effects are small and classical spacetime emerges, often G_N → 0. "the emergence of spacetime in the semi-classical limit."
  • subregion-subalgebra duality: A proposed correspondence identifying bulk spacetime subregions with emergent von Neumann subalgebras of the boundary theory. "A key concept is called the subregion-subalgebra duality~\cite{LeuLiu22}"
  • thermofield double (TFD): A purification of a thermal state as an entangled state of two copies of a system. "As a result, $\ket{\Phi_{\pi \ov 4}$ is the thermofield double (TFD) state of the RR and LL systems at an infinite temperature."
  • type III_1 von Neumann algebra: The unique hyperfinite type III factor relevant to local algebras in relativistic QFT, lacking a trace and with full modular spectrum. "type III1_1"
  • von Neumann algebra: A weakly closed ∗-subalgebra of bounded operators on a Hilbert space that contains the identity. "von Neumann algebras provide a natural framework for describing quantum subsystems when standard tensor factorizations are unavailable"
  • von Neumann’s double commutant theorem: The theorem stating that a ∗-algebra is a von Neumann algebra iff it equals its double commutant. "A fundamental statement about von Neumann algebra\ is von Neumann's double commutant theorem"
  • weight (on a von Neumann algebra): A positive (possibly unnormalized) linear functional generalizing states and traces. "A {\bf weight} $\om$ on $\sM$ is a linear functional that satisfies in addition to~\eqref{iwn}, \be \label{pou} \om (A\da A) \geq 0, \quad \forall A \in \sM \ . \ee"
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts

Authors (1)

  1. Hong Liu
List To Do Tasks Checklist Streamline Icon: https://streamlinehq.com

Collections

Sign up for free to add this paper to one or more collections.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up
X Twitter Logo Streamline Icon: https://streamlinehq.com

Tweets

This paper has been mentioned in 3 tweets and received 114 likes.

Upgrade to Pro to view all of the tweets about this paper:

Start a free 7-day Pro trial