Active Next-Best-View Optimization for Risk-Averse Path Planning (2510.06481v1)

Abstract: Safe navigation in uncertain environments requires planning methods that integrate risk aversion with active perception. In this work, we present a unified framework that refines a coarse reference path by constructing tail-sensitive risk maps from Average Value-at-Risk statistics on an online-updated 3D Gaussian-splat Radiance Field. These maps enable the generation of locally safe and feasible trajectories. In parallel, we formulate Next-Best-View (NBV) selection as an optimization problem on the SE(3) pose manifold, where Riemannian gradient descent maximizes an expected information gain objective to reduce uncertainty most critical for imminent motion. Our approach advances the state-of-the-art by coupling risk-averse path refinement with NBV planning, while introducing scalable gradient decompositions that support efficient online updates in complex environments. We demonstrate the effectiveness of the proposed framework through extensive computational studies.

• The paper introduces a framework that integrates AV@R risk metrics with 3D Gaussian splatting to generate dynamic risk maps for safe navigation.
• The methodology employs Riemannian gradient descent on SE(3) for precise NBV optimization, efficiently refining navigation paths in uncertain environments.
• Results demonstrate improved obstacle clearance and mapping fidelity, significantly advancing risk-aware trajectory planning in robotics.

Active Next-Best-View Optimization for Risk-Averse Path Planning

Introduction

The research paper introduces a framework that addresses the challenges of safe navigation in uncertain environments by integrating risk-averse trajectory planning with active perception. The approach leverages a novel combination of Average Value-at-Risk (AV@R) statistics and 3D Gaussian-splat Radiance Fields to generate risk maps and refine coarse navigation paths. Furthermore, Next-Best-View (NBV) selection is formulated as an optimization problem on the $\mathrm{SE}(3)$ pose manifold using Riemannian gradient descent. This work advances the field of risk-aware navigation by coupling path refinement with next-best-view planning while enabling scalable and efficient online updates.

Problem Formulation

The paper addresses the problem of navigating autonomous robots through unknown or partially known 3D environments under safety constraints. The objective is to refine a given trajectory into a safe path that maximizes information gain related to navigation while keeping computational resources minimal. The robot updates a 3D Gaussian-splat map in real-time, constructing a risk field using AV@R to inform safe trajectory planning. The planning process involves alternating risk-aware path optimization and NBV computation, focusing on areas critical to the robot's immediate movement.

Methodology

The methodology encompasses several key components:

1. 3D Gaussian Splatting: This recent scene representation technique enables efficient and high-fidelity 3D reconstruction. The paper employs it to represent environments and directly ties safety metrics (like AV@R) into the risk assessment process.
2. Risk Quantification: Translating collision risks into measurable quantities, specifically using AV@R, allows for precise safety assessments along planned trajectories. This metric is calculated by evaluating the distribution of signed distances from trajectory points to Gaussian splats and informs path refinement processes.
3. Next-Best-View Optimization: The NBV selection focuses on maximizing proximity-weighted Fisher Information Gain, which emphasizes the importance of nearby Gaussian splats to improve mapping accuracy and safety in the robot's immediate vicinity. Gradient-based optimization on $\mathrm{SE}(3)$ aims to achieve this effectively.

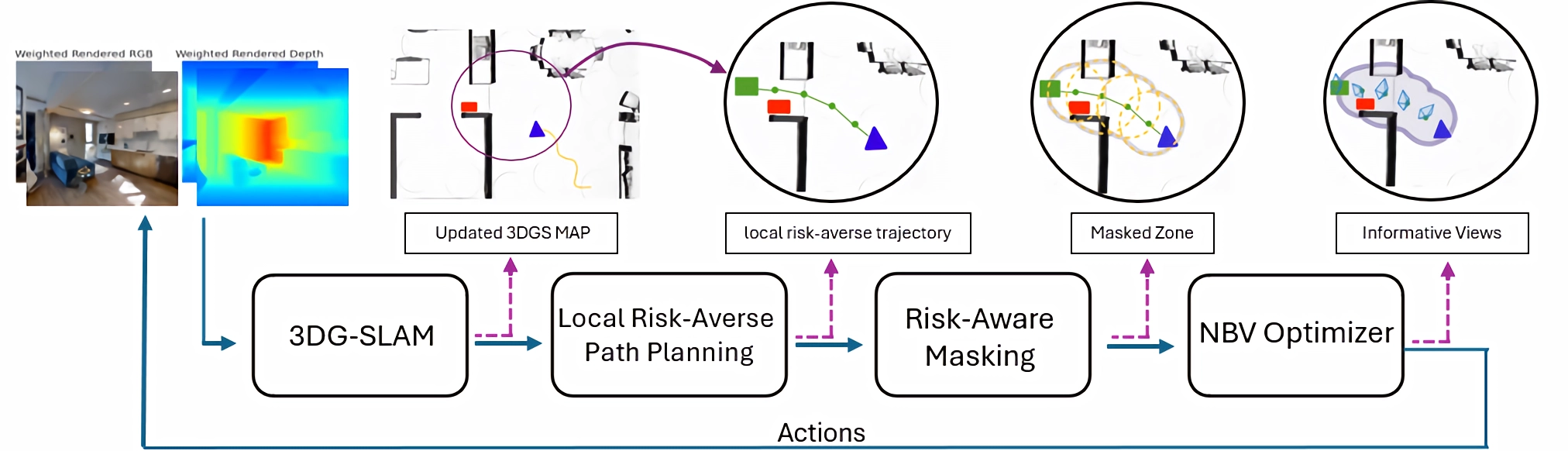
   Figure 1: Block diagram of the proposed risk-averse trajectory planning.

Risk-Aware Trajectory Planning

The authors propose a method that uses Riemannian manifold optimization to integrate trajectory-aware NBV planning, designed specifically to leverage the robot's sensory feedback and environmental updates efficiently. The locally safe trajectory segment replanning is executed dynamically, responding to changing environments by modifying high-risk waypoints into safe proxy subgoals, thus preventing potential collisions without excessive path deviations.

Results and Evaluation

The effectiveness of the proposed framework is demonstrated through extensive computational studies, where the safety of navigation paths is quantified using AV@R. The planning approach significantly improves safety metrics when compared to traditional path planning algorithms, as evidenced by increased clearance from obstacles in simulation environments. Moreover, the integration of NBV results in enhanced 3D mapping fidelity where it matters most: along the robot's planned trajectory.

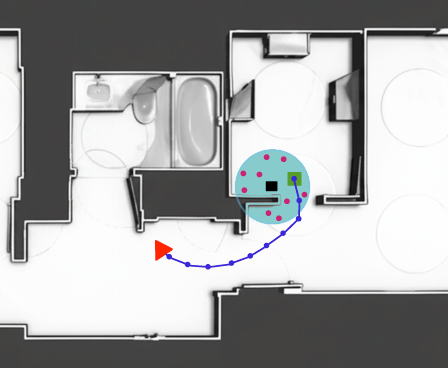
Figure 2: This shows a safe proxy subgoal selection as explained in relevant sections.

Conclusion

This paper provides a novel contribution to autonomous navigation by closely integrating risk analysis with active information gathering. By addressing both the navigation and perceptual challenges in a unified manner, the proposed framework enhances safety and operational efficiency. Future directions might include real-time extensions to handle dynamically changing environments and expanding the framework to even more computationally constrained platforms. Overall, the work lays a substantial foundation for robust, risk-aware navigation in complex robotic applications.