Sample-Efficient and Smooth Cross-Entropy Method Model Predictive Control Using Deterministic Samples (2510.05706v1)

Abstract: Cross-entropy method model predictive control (CEM--MPC) is a powerful gradient-free technique for nonlinear optimal control, but its performance is often limited by the reliance on random sampling. This conventional approach can lead to inefficient exploration of the solution space and non-smooth control inputs, requiring a large number of samples to achieve satisfactory results. To address these limitations, we propose deterministic sampling CEM (dsCEM), a novel framework that replaces the random sampling step with deterministic samples derived from localized cumulative distributions (LCDs). Our approach introduces modular schemes to generate and adapt these sample sets, incorporating temporal correlations to ensure smooth control trajectories. This method can be used as a drop-in replacement for the sampling step in existing CEM-based controllers. Experimental evaluations on two nonlinear control tasks demonstrate that dsCEM consistently outperforms state-of-the-art iCEM in terms of cumulative cost and control input smoothness, particularly in the critical low-sample regime.

• The paper presents dsCEM, a deterministic sampling approach that replaces random sampling in CEM-MPC to achieve smoother and more efficient control.
• It integrates deterministic samples derived from localized cumulative distributions, enhancing exploration and temporal correlations in control trajectories.
• Experimental results on mountain car and cart-pole tasks demonstrate improved control smoothness and faster convergence with fewer samples.

Sample-Efficient and Smooth Cross-Entropy Method Model Predictive Control Using Deterministic Samples

Abstract

The paper presents a novel approach to improve the efficiency and smoothness of Cross-Entropy Method Model Predictive Control (CEM-MPC) by introducing deterministic sample sets. By replacing the traditional random sampling step with deterministic samples derived from Localized Cumulative Distributions (LCDs), the method addresses the inherent challenges of random sampling, which often lead to inefficient exploration and non-smooth control inputs. This approach is demonstrated as a modular drop-in replacement for existing CEM-based controllers, showing improvements in performance, particularly in low-sample regimes on nonlinear control tasks like the mountain car and cart-pole swing-up task.

Introduction

Model Predictive Control (MPC) is essential in solving optimal control problems, especially in nonlinear settings where gradient-based methods struggle with non-differentiable dynamics and non-convex cost functions. The Cross-Entropy Method (CEM), a popular gradient-free optimization technique, integrates effectively into the MPC framework by refining a proposal distribution over control inputs through iterative sampling and evaluation.

The paper addresses the limitations involved in standard CEM-MPC, primarily those stemming from random sampling. Random samples can lead to non-smooth control sequences and require large sample sizes for efficient exploration. Despite improvements like temporal correlations in iCEM, random sampling still constrains smoothness and efficiency. Thus, the authors propose deterministic sampling CEM (dsCEM), leveraging optimal sample sets structured by deterministic distributions. These samples are incorporated with temporal correlations to ensure effective and smooth control trajectories.

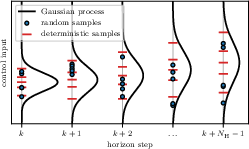
Figure 1: Schematic showing control input sampling over a finite horizon using either deterministic or random samples. As can be seen, deterministic samples cover the stochastic process without large gaps or clusters.

Optimal Control Problem

The paper formalizes the discrete-time, finite-horizon deterministic optimal control problem (OCP) with cumulative cost functions. The OCP seeks to minimize cost over a prediction horizon while adhering to system dynamics and control constraints. The goal is to apply gradient-free methods like CEM-MPC efficiently in this context, using deterministic samples to optimize the control input sequences.

Cross-Entropy Method MPC

CEM is detailed as a method focused on finding optimal densities where samples achieve minimal costs. Parameters are iteratively updated to minimize KL divergence between optimal and proposed distributions. This iterative refinement guides the search toward optimal solutions, applying to MPC where the control sequence is treated as a random vector optimized to minimize cost.

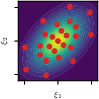
Figure 2: Standard normal samples

Deterministic Sampling Integration

The integration of deterministic samples within the CEM-MPC framework involves pre-computed samples transformed to match the proposal distribution using the LCD methodology. Several schemes, including random rotation and deterministic joint density sampling, introduce variability and enhance exploration across iterations and time steps. The paper also presents methods for adapting covariance structures, emphasizing temporal correlations for smoother, more efficient control sequences.

Experimental Evaluation

Experiments focus on two tasks: the mountain car and cart-pole swing-up. The results demonstrate superior performance of dsCEM variants over iCEM methods, particularly in small sample sizes. dsCEM shows significant improvements in control input smoothness and convergence rate, suggesting enhanced sample efficiency. Notably, dsCEM achieves smoother control sequences than extensive iCEM baselines, highlighting its effectiveness.

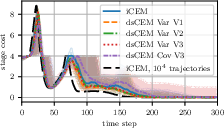
Figure 3: Cumulative costs

Conclusion

The proposed dsCEM framework effectively addresses random sampling limitations in CEM-MPC, suggesting deterministic samples can provide efficient exploration with fewer discrepancies. This modular approach promises improvements in MPC application to complex systems and longer horizons, maintaining real-time capability on constrained hardware.

Future work includes combining dsCEM with learning-based enhancements, like policy-based warm starts, and extending its application to higher-dimensional robotic systems.

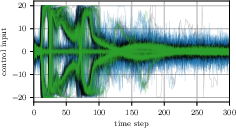
Figure 4: Cumulative costs