Low Frequency Sampling in Model Predictive Path Integral Control

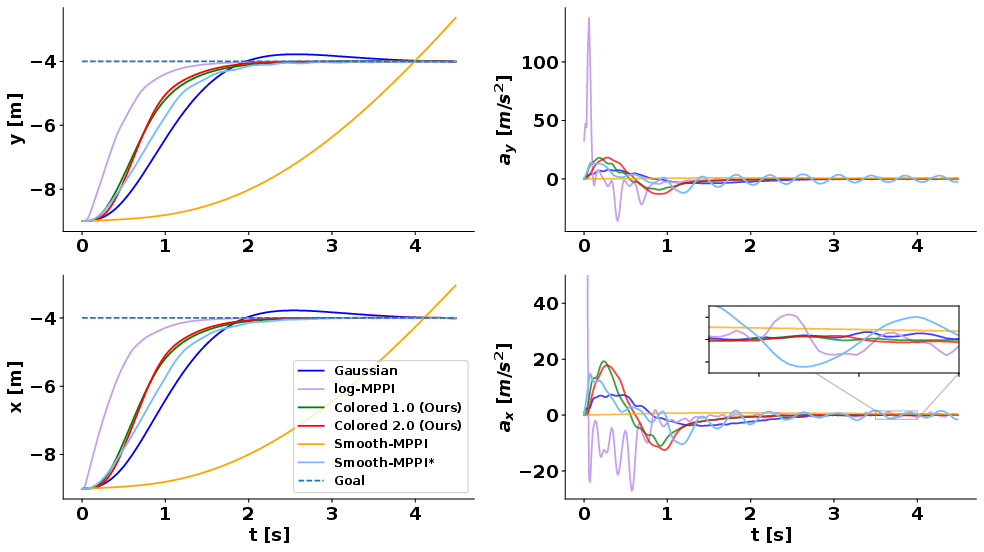
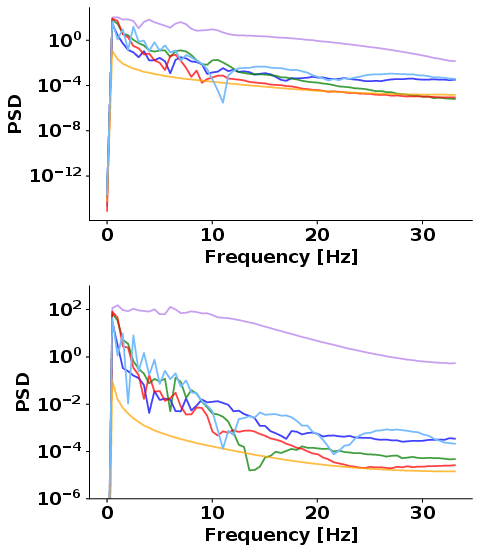
Abstract: Sampling-based model-predictive controllers have become a powerful optimization tool for planning and control problems in various challenging environments. In this paper, we show how the default choice of uncorrelated Gaussian distributions can be improved upon with the use of a colored noise distribution. Our choice of distribution allows for the emphasis on low frequency control signals, which can result in smoother and more exploratory samples. We use this frequency-based sampling distribution with Model Predictive Path Integral (MPPI) in both hardware and simulation experiments to show better or equal performance on systems with various speeds of input response.

• The paper presents a novel colored noise sampling approach in MPPI control to reduce high-frequency noise and achieve smoother trajectories.
• It implements frequency-domain sampling using power spectral density and iFFT techniques, refining the optimization process with minimal adjustments.
• Experimental validations on off-road vehicles and quadrotors demonstrate improved maneuverability, reduced chatter, and faster system stabilization.

Overview of "Low Frequency Sampling in Model Predictive Path Integral Control"

The paper presents advancements in sampling methods for Model Predictive Path Integral (MPPI) control by introducing a colored noise distribution for sampling, in contrast to the traditional uncorrelated Gaussian distribution. The primary objective of this research is to improve the control inputs generated by MPPI, facilitating smoother trajectories and enhanced exploration through a focus on low-frequency control signals. This paper details both simulation and hardware experiments, demonstrating the advantages of colored noise sampling in achieving better performance and smoother trajectories across various scenarios.

Introduction to Sampling-based Model Predictive Control

Sampling-based methods for model-predictive control (MPC) have become essential in navigating complex environments. MPPI, a stochastic optimal control method, has gained prominence due to its applicability to non-linear dynamics without stringent differentiability requirements. However, conventional Gaussian sampling methods have limitations, particularly producing control inputs with high-frequency noise, which can lead to chattering and degradation in system performance over time.

The paper hypothesizes that using colored noise, which emphasizes low-frequency components, can mitigate these issues by generating smoother control signals. Such signals are more akin to human-input trajectories and beneficial for systems with slow input-response characteristics.

Figure 1: The off-road vehicle in a desert terrain just before an autonomy test and a screenshot of the Flightmare quadrotor simulator.

Mathematical Formulation and Implementation

The paper introduces colored noise sampling by leveraging power spectral density ($PSD$) concepts, where noise distributions are crafted with $PSD(f) \propto \frac{1}{f^\gamma}$. This prioritization of low-frequency components is achieved by sampling Gaussian components in the frequency domain and utilizing an inverse Fast Fourier Transform (iFFT) to convert them into time-domain control signals.

This approach retains the theoretical underpinnings of MPPI, requiring only minor adjustments to the optimization process, namely in computing the optimal control trajectory using weighted averages of sampled trajectories. The proposed frequency-based sampling method is seamlessly integrated into the MPPI framework with adjusted update rules and control law derivations.

Figure 2: Samples of state trajectories generated from frequency-based and Gaussian control inputs highlighting smoother and exploratory results with the former.

Experimental Validation

The research involves comprehensive experiments, including:

Off-road Vehicle Platform

Testing on an off-road vehicle highlights the limitations of Gaussian sampling where quick, successive turns are necessary. The colored noise method outperformed Gaussian sampling, enabling the vehicle to negotiate a zig-zag corridor with significantly fewer manual interventions and smoother control trajectories.

Figure 3: Hardware experiments showing the vehicle's maneuverability in a zig-zag corridor using different sampling methods.

Simulated Quadrotor Environment

In a simulated quadrotor environment using the Flightmare simulator, colored noise sampling achieved fast lap times with reduced control signal chatter compared to Gaussian methods. This is critical in real-world applications to prevent hardware fatigue and failure.

Figure 4: Quadrotor flight trajectories comparing Gaussian and Colored sampling, highlighting smoother control inputs with the latter.

Double Integrator Tests

Finally, tests on a double integrator system reveal that colored noise sampling allows for more rapid system stabilization, as it generates control impulses effectively tailored to system dynamics. The method shows robustness across different system configurations.

Figure 5: State and control trajectories with energy power spectral density for quick system stabilization.

Conclusion

This work introduces a novel sampling distribution for MPPI, showcasing its advantages in producing smoother and more efficient control inputs. By emphasizing low-frequency control inputs, the colored noise method enhances exploration capabilities while reducing control signal chatter. These improvements are validated through rigorous experiments involving real and simulated environments, suggesting that frequency-based sampling provides a general framework adaptable to various control scenarios. Future work could explore integrating this method with other advanced MPPI techniques and extending its application to more complex, real-world environments.