Why Low-Precision Transformer Training Fails: An Analysis on Flash Attention (2510.04212v2)
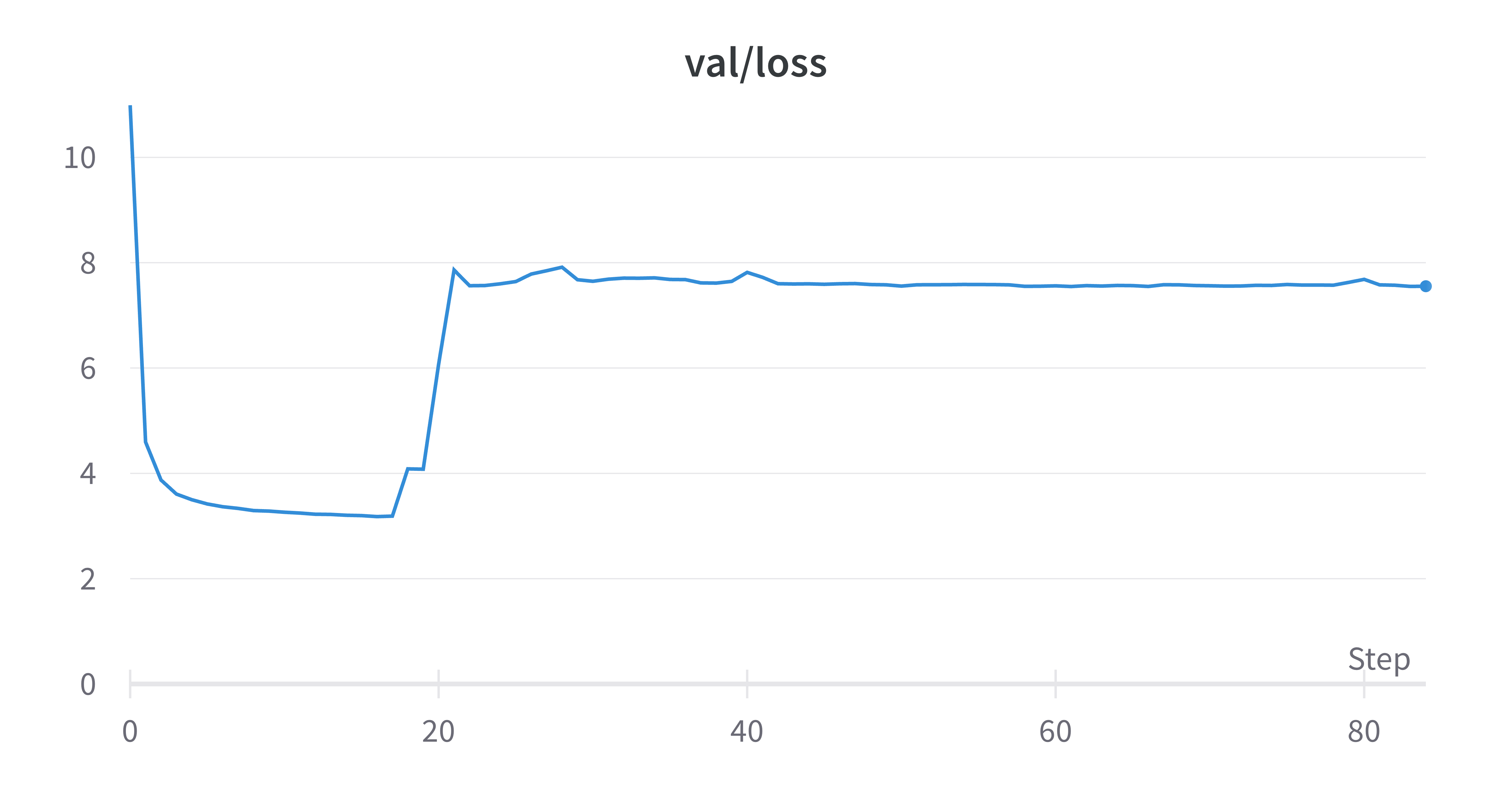
Abstract: The pursuit of computational efficiency has driven the adoption of low-precision formats for training transformer models. However, this progress is often hindered by notorious training instabilities. This paper provides the first mechanistic explanation for a long-standing and unresolved failure case where training with flash attention in low-precision settings leads to catastrophic loss explosion. Our in-depth analysis reveals that the failure is not a random artifact but caused by two intertwined phenomena: the emergence of similar low-rank representations within the attention mechanism and the compounding effect of biased rounding errors inherent in low-precision arithmetic. We demonstrate how these factors create a vicious cycle of error accumulation that corrupts weight updates, ultimately derailing the training dynamics. To validate our findings, we introduce a minimal modification to the flash attention that mitigates the bias in rounding errors. This simple change stabilizes the training process, confirming our analysis and offering a practical solution to this persistent problem. Code is available at https://github.com/ucker/why-low-precision-training-fails.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Practical Applications
Immediate Applications
Below are actionable uses that can be deployed now, derived directly from the paper’s findings and the proposed mitigation.
- Stable Flash Attention (SFA) kernel patch for low-precision training
- Sector: software (ML frameworks), cloud AI platforms, hardware/accelerator vendors
- What: Integrate the paper’s dynamic softmax normalization adjustment into FlashAttention (FA) kernels so attention probabilities never equal 1, preventing biased BF16 rounding and loss explosions.
- Tools/products/workflows: A patched FA2 kernel; upstream PRs to libraries like FlashAttention, xFormers, DeepSpeed; training recipes that enable SFA via a flag.
- Assumptions/dependencies: Access to attention kernel code; softmax shift-invariance holds; careful choice of β (e.g., 2–8) to avoid underflow or re-rounding back to 1; validated on BF16 and tested across GPUs/NPUs.
- Selective FP32 fallback for critical paths or heads
- Sector: software (ML training stacks), cloud AI platforms
- What: Compute only O (the unnormalized PV product) or specific outlier attention heads in FP32 while keeping the rest in BF16 to restore stability with minimal performance impact.
- Tools/products/workflows: Head-level “precision override” hooks; runtime toggles when spectral norms or D = rowsum(d ∘ O) drift.
- Assumptions/dependencies: The instability is localized to a handful of heads; hardware supports mixed precision efficiently.
- Numerical stability telemetry and alerts in training pipelines
- Sector: MLOps, software (observability)
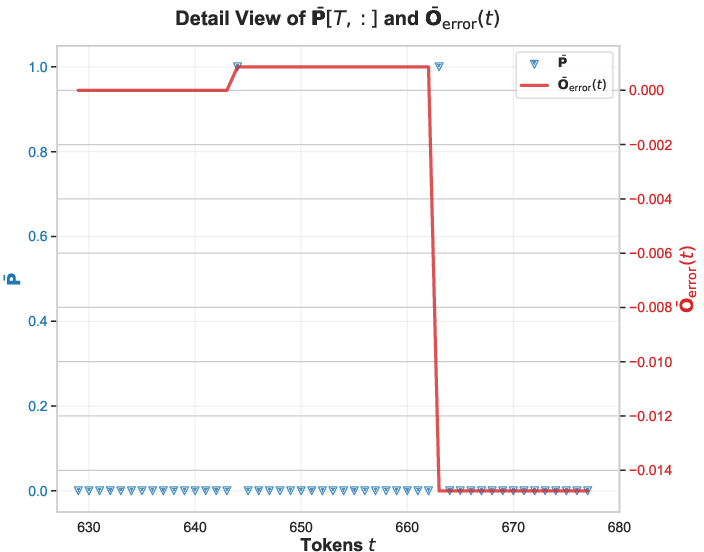
- What: Monitor indicators the paper identified: spectral norms of WQ per head, cumsum of (D_lp − D_hp), counts of rows with multiple identical maxima in QK scores, and frequency of attention probabilities equal to 1.
- Tools/products/workflows: “Precision-aware Attention Monitor (PAM)” dashboard; Spectral Norm Watchdog; logging hooks in PyTorch/TF/JAX.
- Assumptions/dependencies: Access to per-head stats; negligible overhead from instrumentation.
- Training recipe updates to reduce attention sinks that trigger unit probabilities
- Sector: software (LLM training), industry practitioners across domains
- What: Prioritize QK normalization, QK clipping, and Gated Attention to lower the chance of repeated row maxima that lead to attention probabilities of 1.
- Tools/products/workflows: Pre-configured stabilizing attention modules; curriculum of checks that combine with the SFA patch.
- Assumptions/dependencies: Minor hyperparameter tuning; compatibility with FA kernel patches.
- Deterministic reproducibility harness for failure diagnosis
- Sector: academia, industry research
- What: Adopt the paper’s reproducibility tactic (fixed batch sequence) to isolate numerical instabilities and compare low/high precision runs.
- Tools/products/workflows: Deterministic dataloaders and seed management; snapshotting and replay of batch order.
- Assumptions/dependencies: Data pipeline supports recording/reuse; minor I/O overhead acceptable.
- Energy and cost savings from stable BF16 training
- Sector: energy, cloud cost management
- What: Avoid reverting to FP32 or standard attention by deploying SFA; reduce compute, memory bandwidth, and CO2e during LLM training.
- Tools/products/workflows: Cost/energy dashboards that attribute savings to precision-safe kernels.
- Assumptions/dependencies: Stability proven on target model sizes; marginal overhead from SFA patch is negligible.
- Hardware/firmware configurations that minimize rounding bias
- Sector: hardware/accelerators (NVIDIA/AMD/TPU/Ascend)
- What: Where supported, enable stochastic rounding or FP32 accumulation specifically for PV products; choose rounding modes that reduce biases.
- Tools/products/workflows: Driver/firmware flags; kernel-level accumulation modes.
- Assumptions/dependencies: Hardware exposes rounding-mode control; compatibility with FA tiling and SRAM usage.
- Domain model training that benefits immediately from reduced failures
- Sector: healthcare, finance, robotics, education
- What: Stabilize low-precision training for domain-specific LLMs (biomedical, financial NLP, robot policy models, tutoring assistants) to cut training costs and time-to-deploy.
- Tools/products/workflows: Integrate SFA into existing domain pipelines; monitor head-level norms to prevent silent divergence.
- Assumptions/dependencies: Attention-heavy architectures; institutional willingness to update kernels and telemetry.
- Educational materials and labs on floating-point error mechanics
- Sector: education (curriculum for ML systems)
- What: Use the paper’s BF16 rounding and sticky-bit examples to teach numerical analysis in ML; add labs that visualize biased rounding in attention.
- Tools/products/workflows: Jupyter notebooks; visualization widgets showing softmax shifts and rounding steps.
- Assumptions/dependencies: Access to precision-manipulable kernels and reproducible toy models.
- Risk management guardrails in large-scale training
- Sector: MLOps, reliability engineering
- What: Auto-pause/resume when spectral norms spike or (D_lp − D_hp) cumsum drifts; auto-apply FP32 fallback or SFA patch and re-run.
- Tools/products/workflows: Policy rules in orchestration (Kubernetes, Ray, Slurm) tied to numerical telemetry.
- Assumptions/dependencies: Organization buys into “numerical SRE” practices; overhead acceptable.
Long-Term Applications
These applications need further research, scaling, hardware support, or standardization before broad deployment.
- Precision-safe kernel design patterns beyond attention
- Sector: software (compilers/kernels), hardware
- What: Generalize the paper’s approach to other critical ops (e.g., matmul accumulations, normalization) to prevent biased rounding in low precision across the stack.
- Tools/products/workflows: A “numerically stable ops” library; compiler passes that enforce safe normalization and precision orchestration.
- Assumptions/dependencies: Formal analyses of error propagation for each op; integration with graph compilers (XLA/TVM).
- Hardware support for unbiased rounding in training
- Sector: hardware, energy
- What: Incorporate stochastic rounding or hybrid rounding modes as first-class features in GPUs/NPUs to reduce bias in BF16/FP8, especially in accumulation paths.
- Tools/products/workflows: ISA extensions and firmware APIs; hardware validation suites that measure training stability vs energy.
- Assumptions/dependencies: Vendor cooperation; negligible performance penalty; alignment with ML frameworks.
- Automated precision orchestration systems
- Sector: software (ML platforms), cloud
- What: Runtime systems that dynamically elevate precision only for numerically sensitive operations/heads detected via telemetry, reverting after stabilization.
- Tools/products/workflows: Precision controllers integrated with training schedulers; feedback loops driven by spectral norms and identical-maxima counters.
- Assumptions/dependencies: Low-latency detection; safe transitions; minimal impact on throughput.
- Numerical stability certification and standards
- Sector: policy, industry consortia
- What: Create benchmarks and certifications for “precision-safe training” that vendors and cloud providers can meet; include reporting of rounding modes and stability telemetry.
- Tools/products/workflows: Standard test suites; public scorecards; procurement requirements that favor certified kernels/hardware.
- Assumptions/dependencies: Cross-vendor alignment; governance for standard maintenance.
- Expansion to FP8/FP4 and trillion-token scale
- Sector: academia, software, hardware
- What: Investigate whether similar biased low-rank gradient accumulation occurs at lower precisions; develop mitigations compatible with FP8/FP4 formats and massive contexts.
- Tools/products/workflows: Research kernels with tailored normalization strategies; large-scale experiments across hardware.
- Assumptions/dependencies: Access to large training budgets; careful interplay with optimizers and scale rules.
- Numerical error profilers and debuggers for ML stacks
- Sector: software tooling
- What: Build profilers that attribute divergence to specific rounding events (e.g., unit softmax probabilities + negative value distributions), surfacing precise failure chains.
- Tools/products/workflows: “Numerical Error Profiler” integrated with PyTorch/TF/JAX; trace visualizations linking kernels to training dynamics.
- Assumptions/dependencies: Low overhead tracing; standardized metadata from kernels.
- Curriculum and workforce upskilling in numerical ML systems
- Sector: education, industry training
- What: Formal courses on floating-point formats, rounding modes, error propagation, and precision-safe design; required training for ML infra engineers.
- Tools/products/workflows: Standards-aligned syllabi; lab kits; certification pathways.
- Assumptions/dependencies: Institutional adoption; cooperation from frameworks/hardware vendors for educational resources.
- Safer, cheaper on-device and vertical-specific models
- Sector: robotics, healthcare, finance, education, consumer devices
- What: With better precision safety, train smaller models in low precision that can be deployed on edge devices (robots, medical instruments, fintech terminals, classroom tablets) with lower energy footprints.
- Tools/products/workflows: Edge-friendly training/incremental fine-tuning flows; safe-kernel libraries optimized for embedded accelerators.
- Assumptions/dependencies: Stable low-precision kernels across diverse hardware; domain compliance and validation.
- Formal analysis and theory of biased low-rank error accumulation
- Sector: academia
- What: Extend mechanistic understanding and proofs of how rounding bias and emergent low-rank structures interact across architectures, optimizers, and curricula.
- Tools/products/workflows: Theoretical frameworks; validated simulators for floating-point training dynamics.
- Assumptions/dependencies: Cross-disciplinary collaboration (numerical analysis + ML theory); reproducible datasets and kernels.
- Security and robustness considerations for training-time numerical behavior
- Sector: industry research, security
- What: Explore whether adversarial data or curricula can amplify identical maxima and rounding bias to induce failure; design detectors and safeguards.
- Tools/products/workflows: Adversarial training-time tests; runtime mitigations that enforce safe normalization.
- Assumptions/dependencies: Ethical review; careful experimentation to avoid spurious conclusions.
Notes on Assumptions and Dependencies
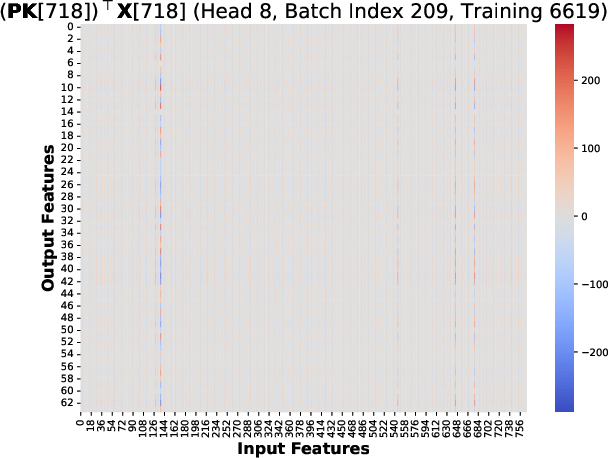
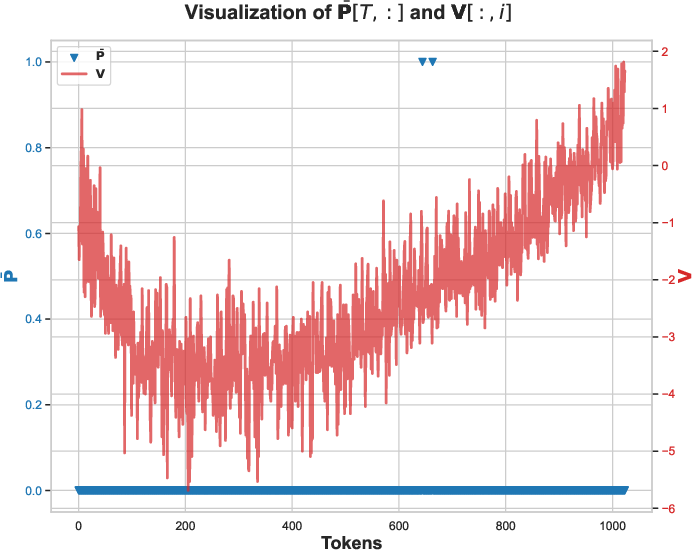
- The failure is tied to BF16’s rounding in the PV product when attention probabilities equal 1 and values are predominantly negative; different hardware rounding policies may alter dynamics.
- The proposed SFA softmax adjustment relies on softmax shift-invariance and a β range that avoids underflow and re-rounding to 1; tuning may be model- and hardware-specific.
- Observed localization to specific attention heads implies monitoring and targeted fixes are effective; generalized fixes still need validation across architectures and precisions (FP8/FP4).
- Tiling is not the root cause, but kernel-level changes must remain I/O-aware and SRAM-friendly to preserve FA’s performance benefits.
Collections
Sign up for free to add this paper to one or more collections.