Neural Jump ODEs as Generative Models (2510.02757v1)

Abstract: In this work, we explore how Neural Jump ODEs (NJODEs) can be used as generative models for It^o processes. Given (discrete observations of) samples of a fixed underlying It^o process, the NJODE framework can be used to approximate the drift and diffusion coefficients of the process. Under standard regularity assumptions on the It^o processes, we prove that, in the limit, we recover the true parameters with our approximation. Hence, using these learned coefficients to sample from the corresponding It^o process generates, in the limit, samples with the same law as the true underlying process. Compared to other generative machine learning models, our approach has the advantage that it does not need adversarial training and can be trained solely as a predictive model on the observed samples without the need to generate any samples during training to empirically approximate the distribution. Moreover, the NJODE framework naturally deals with irregularly sampled data with missing values as well as with path-dependent dynamics, allowing to apply this approach in real-world settings. In particular, in the case of path-dependent coefficients of the It^o processes, the NJODE learns their optimal approximation given the past observations and therefore allows generating new paths conditionally on discrete, irregular, and incomplete past observations in an optimal way.

• The paper introduces Neural Jump ODEs to estimate drift and diffusion from irregular, discrete data, enabling generation of sample paths that match the true process.
• It employs a predictive, non-adversarial training framework with bias correction, ensuring convergence and robustness even under missing data and path-dependence.
• Empirical evaluations on GBM and OU processes demonstrate the method's ability to replicate both marginal and pathwise distributions accurately.

Neural Jump ODEs as Generative Models: Theory and Practice

Overview

"Neural Jump ODEs as Generative Models" (2510.02757) presents a framework for learning the law of Itô processes from discrete, potentially irregular and incomplete observations, using Neural Jump ODEs (NJODEs). The approach enables the estimation of drift and diffusion coefficients directly from data, facilitating the generation of new sample paths that match the true underlying process in law. The method is non-adversarial, prediction-based, and robust to missing data and path-dependent dynamics, with theoretical guarantees of convergence under standard regularity assumptions.

Problem Formulation and Motivation

The central problem is to learn the law of a $d$-dimensional Itô process $X$ governed by the SDE:

$$dX_t = \mu_t(X_{\cdot \wedge t})\,dt + \sigma_t(X_{\cdot \wedge t})\,dW_t,$$

where $\mu_t$ and $\sigma_t$ are unknown, possibly path-dependent drift and diffusion coefficients, and $W_t$ is an $m$-dimensional Brownian motion. The only available data are discrete, possibly irregular and incomplete, observations of independent sample paths of $X$.

The objective is to generate new, independent trajectories of $X$ by learning estimators $\hat\mu_t$ and $\hat\sigma_t$ for the coefficients, such that the generated process $\tilde X$ matches the law of $X$ as closely as possible.

NJODE Framework for Coefficient Estimation

NJODEs are continuous-time models designed to optimally predict stochastic processes from discrete, irregular, and incomplete observations. The key insight is that, by training NJODEs to approximate conditional expectations of $X_t$ and $X_t X_t^\top$ given the available information, one can construct estimators for the drift and diffusion coefficients.

Drift Estimation

Given observations up to time $t$, the drift is estimated via:

$$\hat{\mu}_t^\Delta = \frac{E[X_{t+\Delta} | \mathcal{A}_t] - X_t}{\Delta},$$

where $\mathcal{A}_t$ is the $\sigma$-algebra generated by the available information up to $t$. The NJODE is trained to predict $E[X_{t+\Delta} | \mathcal{A}_t]$.

Diffusion Estimation

The diffusion is estimated using the conditional expectation of squared increments:

$$\hat{\Sigma}_t^\Delta = \frac{1}{\Delta} E\left[(X_{t+\Delta} - X_t)(X_{t+\Delta} - X_t)^\top \mid \mathcal{A}_t\right].$$

To ensure positive semi-definiteness, the NJODE is trained to output a matrix $G$ and the estimator is taken as $S = GG^\top$.

Instantaneous Estimation

To reduce bias from finite $\Delta$, the paper introduces direct estimation of instantaneous coefficients by training NJODEs to predict the quotient of increments (for drift) and squared increments (for diffusion), divided by the time step, and using right-limits at observation times.

Generative Procedure

Once the NJODEs are trained, the generative procedure is as follows:

1. Initialization: Start from an initial observation or a sequence of observations (possibly with missing values).
2. Iterative Generation: At each step, use the current history to compute $\hat\mu_t$ and $\hat\sigma_t$ via the NJODEs, then sample the next point using the Euler-Maruyama scheme:

$$\tilde X_{t+\Delta} = \tilde X_t + \hat\mu_t \Delta + \hat\sigma_t \Delta W_t.$$

1. Continuation: Repeat until the desired time horizon is reached.

This procedure can generate unconditional sample paths or paths conditioned on arbitrary observed histories.

Theoretical Guarantees

The paper provides rigorous convergence results:

• Consistency: Under standard regularity and identifiability assumptions, as the NJODEs are trained to optimality and $\Delta \to 0$, the estimators $\hat\mu_t$ and $\hat\sigma_t$ converge in $L^2$ to the true coefficients (or their $L^2$-optimal projections given the available information).
• Law Convergence: The law of the generated process $\tilde X$ converges to the law of the true process $X$ as the estimators improve and the discretization is refined.
• Robustness: The approach is robust to irregular sampling, missing data, and path-dependent coefficients.

Empirical Evaluation

The framework is validated on synthetic datasets, including geometric Brownian motion (GBM) and Ornstein-Uhlenbeck (OU) processes. Four estimation strategies are compared: baseline, joint baseline with bias reduction, instantaneous, and joint instantaneous with bias reduction.

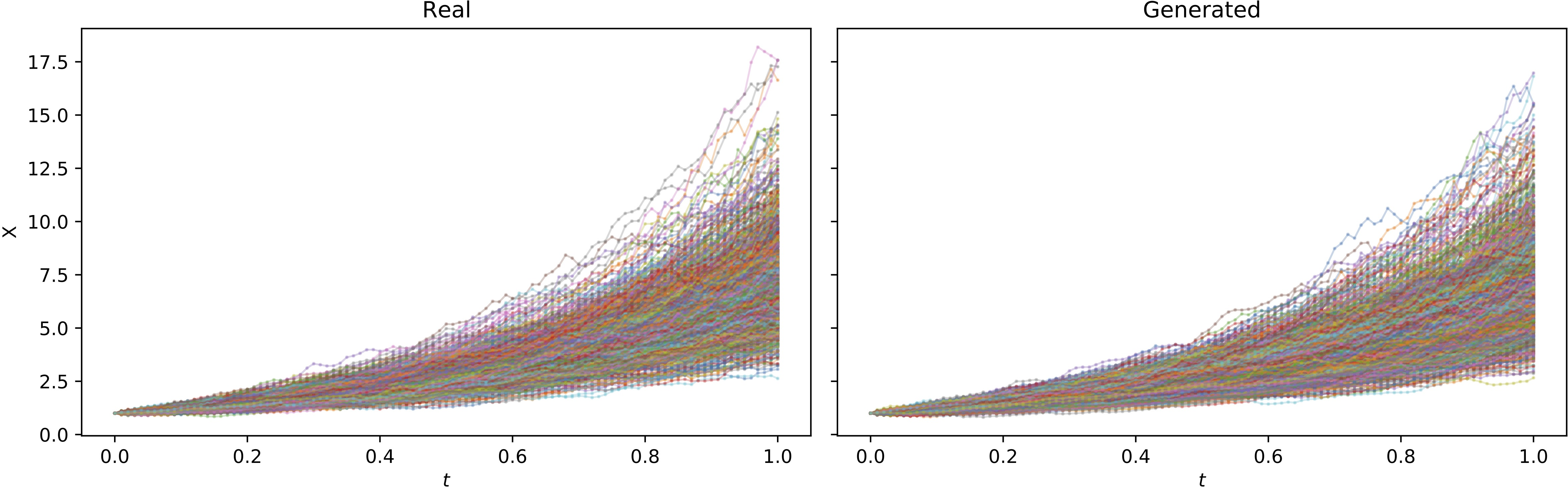
Figure 1: Plot of true training paths and generated (with joint instantaneous method) paths, with 1000 samples each.

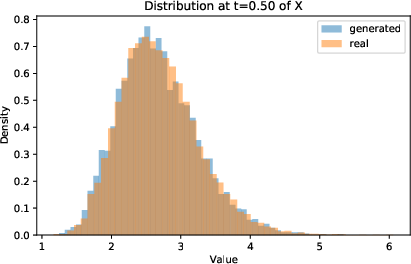
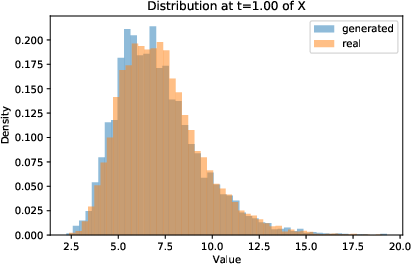
Figure 2: Distribution of $X_t$ at $t=0.5$ and $t=T=1$ of true training paths and generated (with joint instantaneous method) paths.

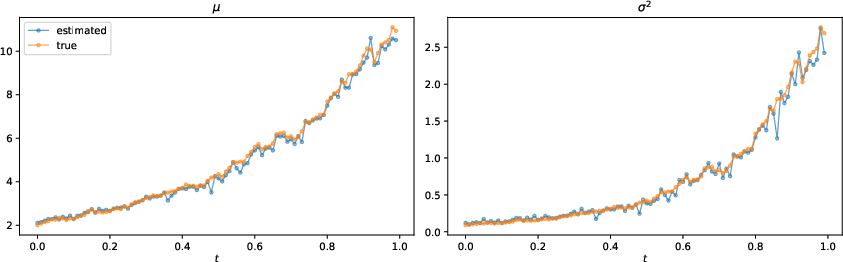
Figure 3: True and estimated (with joint instantaneous method) drift and diffusion coefficients along one generated path.

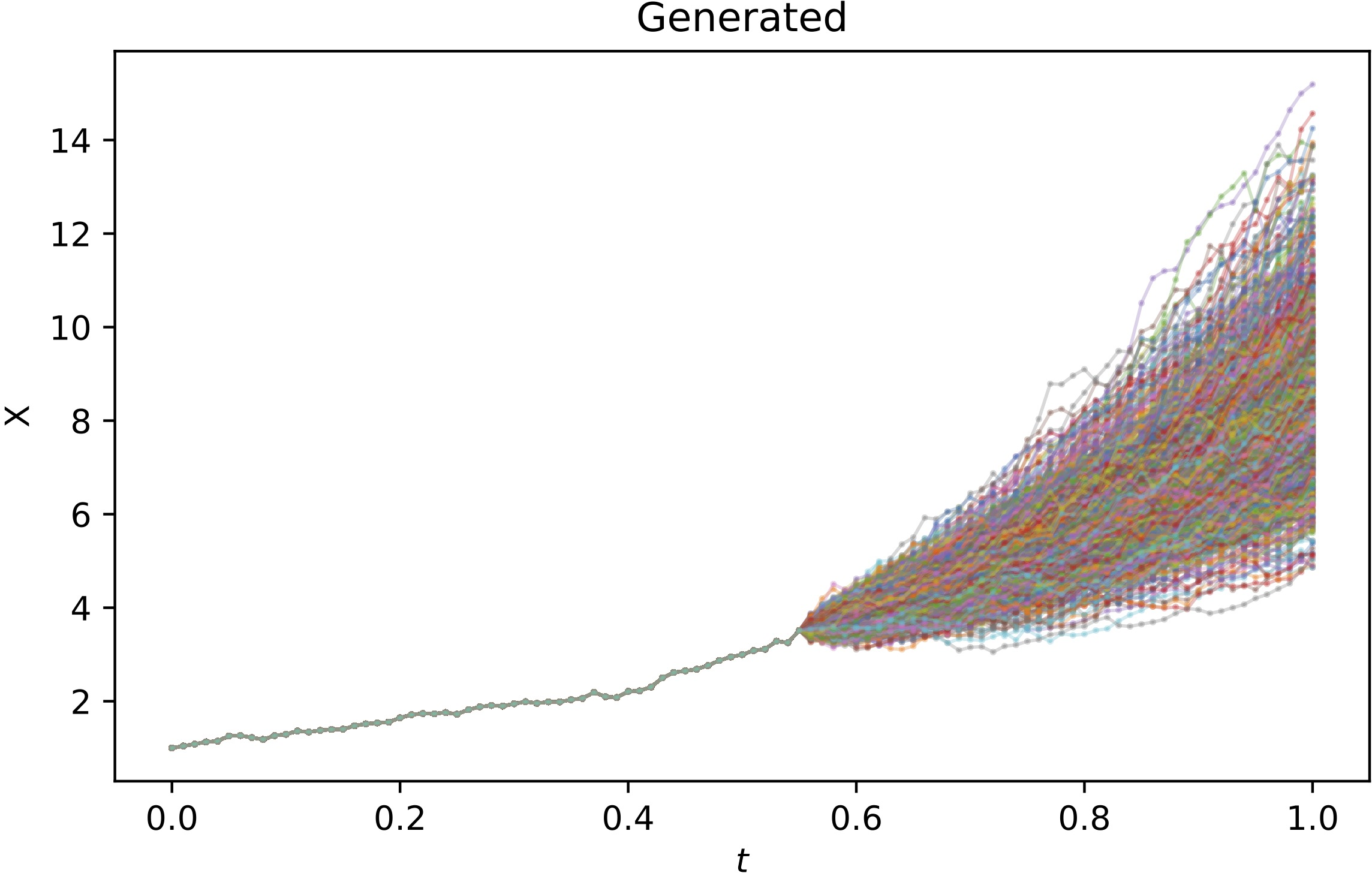
Figure 4: 1000 generated (with joint instantaneous method) path continuations, starting from the history of the first training path until $t=0.55$.

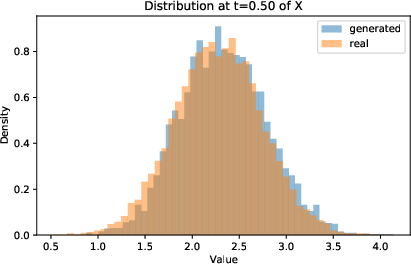
Figure 5: Distribution of $X_t$ at $t=0.5$ and $t=T=1$ of true training paths and generated (with joint instantaneous method) paths.

Key empirical findings:

• The joint instantaneous method with bias reduction yields generated samples whose estimated parameters closely match those of the training data, with negligible invalid paths.
• Marginal and pathwise distributions of generated samples are visually and quantitatively indistinguishable from the true process.
• The method is effective even when the underlying process violates some theoretical assumptions (e.g., unbounded coefficients in GBM).

Implementation Considerations

• Model Architecture: The NJODE is implemented as a neural ODE with jump updates at observation times, using feedforward networks for the drift, jump, and output mappings.
• Training: Models are trained with MSE-type losses on conditional expectations, with optional bias correction for diffusion estimation.
• Computational Requirements: Training is efficient due to the non-adversarial, prediction-based loss, and does not require sample generation during training.
• Scalability: The approach is scalable to high-dimensional and path-dependent processes, and naturally accommodates missing and irregular data.

Comparison to Related Work

Unlike adversarial generative models (e.g., neural SDE-GANs), the NJODE approach is purely predictive, avoids issues of mode collapse and instability, and provides theoretical convergence guarantees. It also improves upon direct coefficient learning in neural SDEs by handling incomplete data and providing law-level convergence, not just marginal matching.

Implications and Future Directions

The NJODE-based generative modeling framework offers a principled, efficient, and robust approach for learning and simulating complex stochastic processes from partial, irregular data. Its ability to handle path-dependence and missingness makes it particularly suitable for real-world applications in finance, physics, and biology.

Potential future developments include:

• Extension to jump-diffusion and Lévy processes.
• Integration with control and reinforcement learning for stochastic systems.
• Application to high-dimensional, multivariate time series with complex dependencies.
• Further improvements in estimator bias correction and uncertainty quantification.

Conclusion

The paper establishes NJODEs as a theoretically sound and practically effective tool for generative modeling of Itô processes from discrete, irregular, and incomplete observations. The framework's convergence guarantees, empirical performance, and flexibility position it as a strong alternative to adversarial and marginal-matching generative models for stochastic processes.