Neural Jump Ordinary Differential Equations: Consistent Continuous-Time Prediction and Filtering

Abstract: Combinations of neural ODEs with recurrent neural networks (RNN), like GRU-ODE-Bayes or ODE-RNN are well suited to model irregularly observed time series. While those models outperform existing discrete-time approaches, no theoretical guarantees for their predictive capabilities are available. Assuming that the irregularly-sampled time series data originates from a continuous stochastic process, the $L^2$-optimal online prediction is the conditional expectation given the currently available information. We introduce the Neural Jump ODE (NJ-ODE) that provides a data-driven approach to learn, continuously in time, the conditional expectation of a stochastic process. Our approach models the conditional expectation between two observations with a neural ODE and jumps whenever a new observation is made. We define a novel training framework, which allows us to prove theoretical guarantees for the first time. In particular, we show that the output of our model converges to the $L^2$-optimal prediction. This can be interpreted as solution to a special filtering problem. We provide experiments showing that the theoretical results also hold empirically. Moreover, we experimentally show that our model outperforms the baselines in more complex learning tasks and give comparisons on real-world datasets.

• The paper introduces NJ-ODE, a framework that integrates jump mechanisms with neural ODEs to yield L2-optimal continuous-time predictions.
• It employs a novel jump neural network for hidden state updates, providing theoretical convergence and reduced complexity.
• Empirical results on financial and real-world datasets confirm NJ-ODE's superior accuracy in modeling irregular stochastic processes.

Neural Jump Ordinary Differential Equations: Consistent Continuous-Time Prediction and Filtering

The paper "Neural Jump Ordinary Differential Equations: Consistent Continuous-Time Prediction and Filtering" introduces the Neural Jump Ordinary Differential Equation (NJ-ODE) framework. This framework extends neural ODEs by incorporating jump mechanisms to model the conditional expectation of stochastic processes with irregular observations. The paper demonstrates the NJ-ODE's theoretical convergence and shows its superior empirical performance compared to existing models like GRU-ODE-Bayes and ODE-RNN.

Model Overview

NJ-ODE combines the strengths of RNNs and neural ODEs to continuously model stochastic processes while accommodating jumps at observation times. Unlike ODE-RNNs, which rely on RNN cells to update hidden states, NJ-ODE employs a simpler approach using a neural network jump mechanism. This choice reduces complexity and allows for theoretical convergence guarantees, emphasizing that NJ-ODE outputs converge to the $L^2$-optimal prediction or conditional expectation.

Implementation Details

Architecture

NJ-ODE consists of several components:

• Neural ODE: Captures continuous latent dynamics between observations.
• Jump Mechanism: Updates hidden states at observation times without relying on prior hidden states, using a standalone neural network.
• Output Mapping: Translates the hidden states to predictions via an output neural network.

def NJ_ODE(x, timesteps, model_params): h_t = initialize_hidden_state(x[0]) predictions = [] for i in range(1, len(timesteps)): h_t = ODESolve(h_t, timesteps[i-1], timesteps[i], model_params) if timesteps[i] in observation_times: h_t = jumpNN(x[timesteps[i]], model_params) predictions.append(outputNN(h_t, model_params)) return predictions

Training

Training involves minimizing a novel loss function that balances fitting observed values and maintaining continuity between observations. The convergence guarantees provided by the NJ-ODE's framework are largely due to the precise mathematical formulations and loss function design.

Experimental Results

NJ-ODE was tested on synthetic datasets (Black-Scholes, Ornstein-Uhlenbeck, and Heston models) and real-world datasets (such as climate data and physiological recordings). The empirical results show that NJ-ODE consistently outperforms GRU-ODE-Bayes, especially in more complex scenarios like the Heston model.

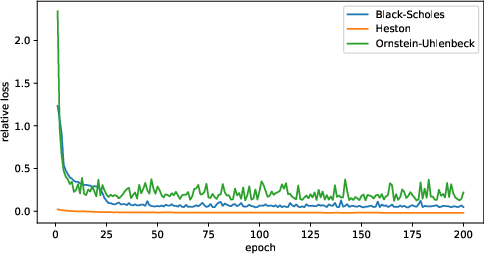
Figure 1: Predicted and true conditional expectation on a test sample of the Heston dataset.

The NJ-ODE's superior performance is largely attributed to its robust handling of irregular time-series data and its ability to model complex non-linearities present in stochastic processes.

Figure 2: Black-Scholes dataset. Mean $\pm$ standard deviation (black bars) of the evaluation metric for varying training samples $N_1$ and network size $M$.

Implications and Future Work

NJ-ODE offers a robust framework for modeling stochastic processes in finance, healthcare, and climate science. By eschewing the need for continuous information between observations, NJ-ODE makes online updates feasible, which is crucial for real-time applications. Future research could extend NJ-ODEs to capture dependencies across multiple stochastic processes or enhance scalability for large datasets.

Conclusion

The NJ-ODE model represents a significant advancement in continuous-time prediction for irregularly sampled stochastic processes. Its theoretical rigor and empirical success suggest potential for widespread application across fields that rely on time-series data. The integration of jumps into the neural ODE framework addresses a critical gap in continuous-time modeling, facilitating both theoretical developments and practical implementations.