Score Distillation of Flow Matching Models (2509.25127v1)

Abstract: Diffusion models achieve high-quality image generation but are limited by slow iterative sampling. Distillation methods alleviate this by enabling one- or few-step generation. Flow matching, originally introduced as a distinct framework, has since been shown to be theoretically equivalent to diffusion under Gaussian assumptions, raising the question of whether distillation techniques such as score distillation transfer directly. We provide a simple derivation -- based on Bayes' rule and conditional expectations -- that unifies Gaussian diffusion and flow matching without relying on ODE/SDE formulations. Building on this view, we extend Score identity Distillation (SiD) to pretrained text-to-image flow-matching models, including SANA, SD3-Medium, SD3.5-Medium/Large, and FLUX.1-dev, all with DiT backbones. Experiments show that, with only modest flow-matching- and DiT-specific adjustments, SiD works out of the box across these models, in both data-free and data-aided settings, without requiring teacher finetuning or architectural changes. This provides the first systematic evidence that score distillation applies broadly to text-to-image flow matching models, resolving prior concerns about stability and soundness and unifying acceleration techniques across diffusion- and flow-based generators. We will make the PyTorch implementation publicly available.

• The paper introduces a unified framework that demonstrates the equivalence between Gaussian diffusion and flow matching objectives using score distillation techniques.
• It extends Score identity Distillation (SiD) to flow-matching models, achieving efficient, high-quality text-to-image synthesis in just four sampling steps.
• Empirical evaluations reveal competitive FID, CLIP, and GenEval scores across models ranging from 0.6B to 12B parameters, showcasing robust scalability.

Score Distillation of Flow Matching Models: A Unified Framework for Fast Text-to-Image Generation

Introduction and Motivation

Diffusion models have established state-of-the-art performance in image synthesis, but their slow iterative sampling remains a significant bottleneck for practical deployment. Recent advances in distillation have enabled one- or few-step generation, dramatically accelerating inference. Flow matching, originally proposed as a distinct generative modeling paradigm, has been shown to be theoretically equivalent to diffusion under Gaussian assumptions. This equivalence raises a critical question: can the highly effective score distillation techniques developed for diffusion models be directly applied to flow-matching models, particularly for text-to-image (T2I) generation with large-scale architectures such as DiT, SANA, SD3, and FLUX?

This work provides a rigorous theoretical and empirical investigation of this question. The authors present a unified derivation—eschewing SDE/ODE formalism in favor of Bayes’ rule and conditional expectations—that demonstrates the equivalence of Gaussian diffusion and flow matching objectives, up to differences in loss weighting and timestep scheduling. Building on this, they extend Score identity Distillation (SiD) to a broad class of pretrained flow-matching T2I models, showing that with minimal adaptation, SiD can distill these models into efficient four-step generators in both data-free and data-aided settings.

Theoretical Unification of Diffusion and Flow Matching

The core theoretical contribution is a derivation that unifies the objectives of Gaussian diffusion and flow matching models. All such models corrupt data via a linear combination of the clean image and Gaussian noise:

$$x_t = \alpha_t x_0 + \sigma_t \epsilon, \quad \epsilon \sim \mathcal{N}(0, I)$$

where the @@@@1@@@@ (SNR) $\text{SNR}_t = \alpha_t^2 / \sigma_t^2$ monotonically decreases with $t$.

The authors show that the optimal solutions for $x_0$-prediction, $\epsilon$-prediction, $v$-prediction, and velocity-prediction in rectified flow are all linear transformations of the conditional mean $\mathbb{E}[x_0 | x_t]$. The only substantive difference between these formulations is the weighting of timesteps in the training loss, which determines the effective influence of each $t$ on the learned parameters.

This is formalized by expressing the overall loss as:

$$L_\phi = \mathbb{E}_{t \sim p(t)} \mathbb{E}_{x_t \sim p(x_t)}\left[ w_t \cdot \frac{\alpha_t^2}{\sigma_t^2} L_\phi(x_t) \right]$$

where $w_t$ is a weighting factor and $p(t)$ is the timestep distribution. The product $w_t p(t)$ defines the effective weight-normalized distribution $\pi(t)$ over timesteps. The practical implication is that, for Gaussian-based models, the choice of $w_t$ and $p(t)$—not the underlying generative process—determines empirical performance differences.

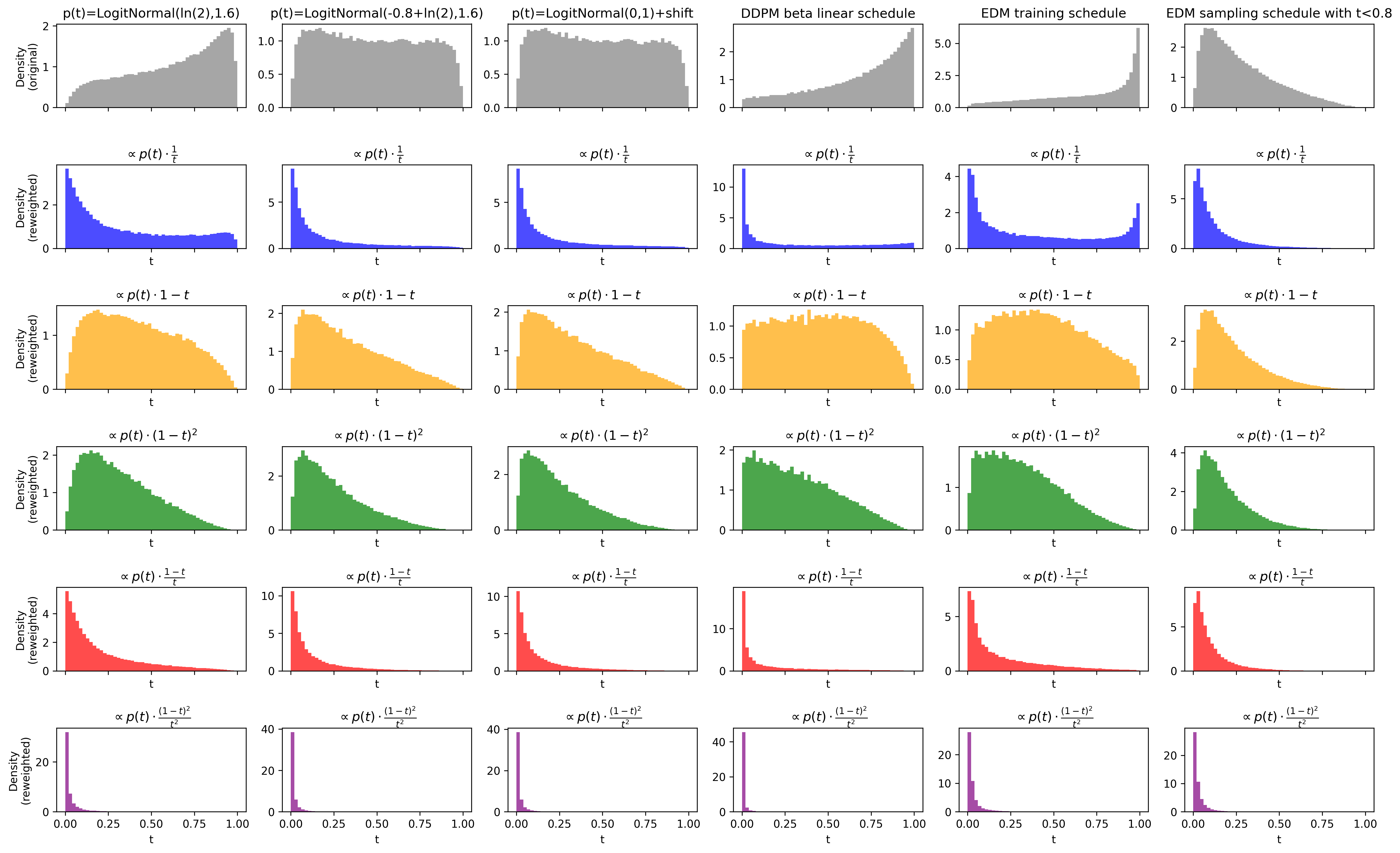
Figure 1: Density plots of various noise schedules mapped to $t \in (0, 1)$ by aligning their SNR, illustrating the effect of different weighting schemes on the effective timestep distribution.

Score Distillation for Flow-Matching Models

The SiD framework, previously validated for diffusion models, is extended to flow-matching models with DiT backbones. The key insight is that the teacher’s $x_0$-prediction can be recovered from the velocity prediction via:

$$f_{\phi}(x_t, t, c) = x_t - t v_{\phi}^{\text{FM}}(x_t, t, c)$$

where $c$ is the text condition. Classifier-free guidance (CFG) is incorporated by linearly combining conditional and unconditional predictions, with a default scale of 4.5.

The distilled generator is trained using Fisher divergence minimization in a data-free setting, alternating updates between the generator and a “fake” flow-matching network initialized from the teacher. The generator loss is:

$$L_{\theta}(x_t^{(k)}) = w_t \left(f_{\phi}(x_t^{(k)}, t_k, c) - f_{\psi}(x_t^{(k)}, t_k, c)\right)^{T} \left(f_{\psi}(x_t^{(k)}, t_k, c) - x_g^{(k)}\right)$$

where $w_t = 1 - t$ by default.

When additional data are available, adversarial learning is incorporated via DiffusionGAN, using spatial pooling of DiT features for the discriminator, without introducing extra parameters.

Empirical Evaluation

The SiD-DiT framework is evaluated on a diverse set of flow-matching T2I models: SANA (rectified flow and TrigFlow), SD3-Medium, SD3.5-Medium, SD3.5-Large, and FLUX.1-dev, spanning 0.6B to 12B parameters. The experiments demonstrate:

• Data-free distillation: SiD-DiT achieves FID, CLIP, and GenEval scores comparable to or better than the teacher models, with only four sampling steps.
• Adversarial enhancement: Incorporating additional data via adversarial loss (SiD$_2^a$-DiT) further reduces FID, especially for SANA and SD3 models.
• Scalability: The method scales to large models (e.g., SD3.5-Large, FLUX.1-dev) using BF16 and FSDP, with a single codebase and minimal hyperparameter tuning.
• Robustness: The same training configuration is effective across all tested architectures and parameter scales.

  Figure 2: Qualitative results of the four-step SiD-DiT generator distilled from SD3.5-Large in a data-free setting.

  

  Figure 3: Qualitative results of the four-step SiD-DiT generator distilled from FLUX-1.DEV in a data-free setting.

  

  Figure 4: Qualitative results of the four-step SiD-DiT and SiD$_2^a$-DiT generators distilled from SD3-Medium, compared against Flash Diffusion SD3 and the teacher model SD3-Medium.

  

  Figure 5: Qualitative results of the four-step SiD-DiT and SiD$_2^a$-DiT generators distilled from SD3.5-Medium, compared against SD3.5-Turbo-Medium and the teacher model SD3.5-Medium.

  

  Figure 6: Qualitative results from the four-step SiD-DiT and SiD$_2^a$-DiT generators distilled from SD3.5-Large, compared against SD3.5-Turbo-Large and the teacher SD3.5-Large.

  

  Figure 7: Qualitative results from the four-step SiD-DiT and SiD$_2^a$-DiT generators distilled from the SANA-Sprint teacher (1.6B), compared against SANA-Sprint 1.6B and the teacher.

Analysis of Loss Reweighting and Timestep Scheduling

The empirical paper of loss reweighting reveals that restricting the generator loss to higher $t$ intervals (i.e., heavier noise) yields visually appealing but less detailed images, while lower $t$ intervals enhance detail at the expense of vividness. The chosen combination of $p(t)$ and $w_t$ in SiD-DiT provides full coverage over $t$, balancing these trade-offs and delivering strong performance across all tested models.

Figure 8: Qualitative generations from distilled SANA by restricting $t$ to different intervals, illustrating the effect of loss reweighting on image characteristics.

Implementation Considerations

• Precision and memory: AMP and BF16 are used to maximize throughput and minimize memory usage, with BF16 required for the largest models.
• Distributed training: FSDP is employed for efficient multi-GPU training.
• Data-free operation: SiD-DiT requires no real images, relying solely on the teacher model for supervision.
• Adversarial extension: When additional data are available, adversarial loss can be incorporated without architectural changes.

Implications and Future Directions

This work provides the first systematic evidence that score distillation applies broadly to flow-matching T2I models, resolving prior concerns about stability and soundness. The unified theoretical perspective clarifies that practical differences between diffusion and flow matching arise primarily from loss weighting and timestep scheduling, not from the generative process itself.

Practically, this enables the rapid distillation of large-scale T2I models into efficient few-step generators, facilitating deployment in latency-sensitive applications. The approach is robust across architectures and parameter scales, requiring minimal adaptation.

Theoretically, the results suggest that future research on generative modeling and fast sampling can focus on unified frameworks that abstract away from the specifics of diffusion or flow matching, instead optimizing the effective weighting of training losses and timestep schedules.

Potential future developments include:

• Tailoring distillation objectives to model-specific guidance mechanisms (e.g., learned guidance in FLUX).
• Systematic exploration of loss reweighting and timestep scheduling for further performance gains.
• Extending the framework to non-Gaussian or non-linear generative processes.

Conclusion

The paper establishes a unified theoretical and empirical foundation for score distillation in flow-matching models, demonstrating that efficient, high-quality, few-step text-to-image generation is achievable across a wide range of architectures with a single, robust framework. This work bridges the gap between diffusion and flow matching, providing a practical path forward for scalable, accelerated generative modeling.