Two-Scale Latent Dynamics for Recurrent-Depth Transformers (2509.23314v1)
Abstract: Recurrent-depth transformers scale test-time compute by iterating latent computations before emitting tokens. We study the geometry of these iterates and argue for a simple, \emph{two-scale} operational picture: (i) within a looped block, updates act as \emph{small-scale refinements}; (ii) across consecutive blocks, states undergo a \emph{larger-scale drift}. Across checkpoints, our measurements show that loop steps become \emph{smaller} and increasingly \emph{orthogonal} to one another, indicating better local modeling of fine structure rather than merely pushing in a single direction. These dynamics motivate an early-exit mechanism based on the model's second-order difference in step-size, which we show is superior in terms of performance, stability and time-efficiency, when compared to the KL-divergence exit strategy of Geiping et al. and its naive first-order counterpart.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Easy-to-Understand Summary of “Two-Scale Latent Dynamics for Recurrent-Depth Transformers”
Overview
This paper looks at how a LLM can “think harder” before saying the next word—without typing out extra words. Instead of making the model write longer explanations, the authors let the model do extra internal processing (silent thinking) on its hidden representation. They then paper the shape and pattern of this internal thinking and use what they learn to make the model stop its extra thinking at the right time, saving time while keeping quality high.
What were the researchers trying to find out?
In simple terms, they asked:
- When a model repeats a block of its own computations (loops) before producing the next word, what kind of movement does its internal state make?
- Is there a recognizable pattern to these movements?
- Can we use that pattern to decide when the model has “thought enough” and should stop looping to give an answer quickly without losing accuracy?
How did they paper it? (Methods explained with analogies)
Think of the model as a person writing a sentence. Before writing the next word, the person can:
- Pause and mentally revise their idea a few times (silent thinking in “latent space”).
- Then finally write the next word.
The authors made a GPT-2–like model with a few “looped” layers. In these layers, the model can repeat its internal computation several times before moving on. They watched what happens to the model’s hidden state (its internal “idea”) at each loop step.
They measured two simple things:
- Step size: How big is the change from one loop step to the next? (Like how much your idea shifts each time you rethink it.)
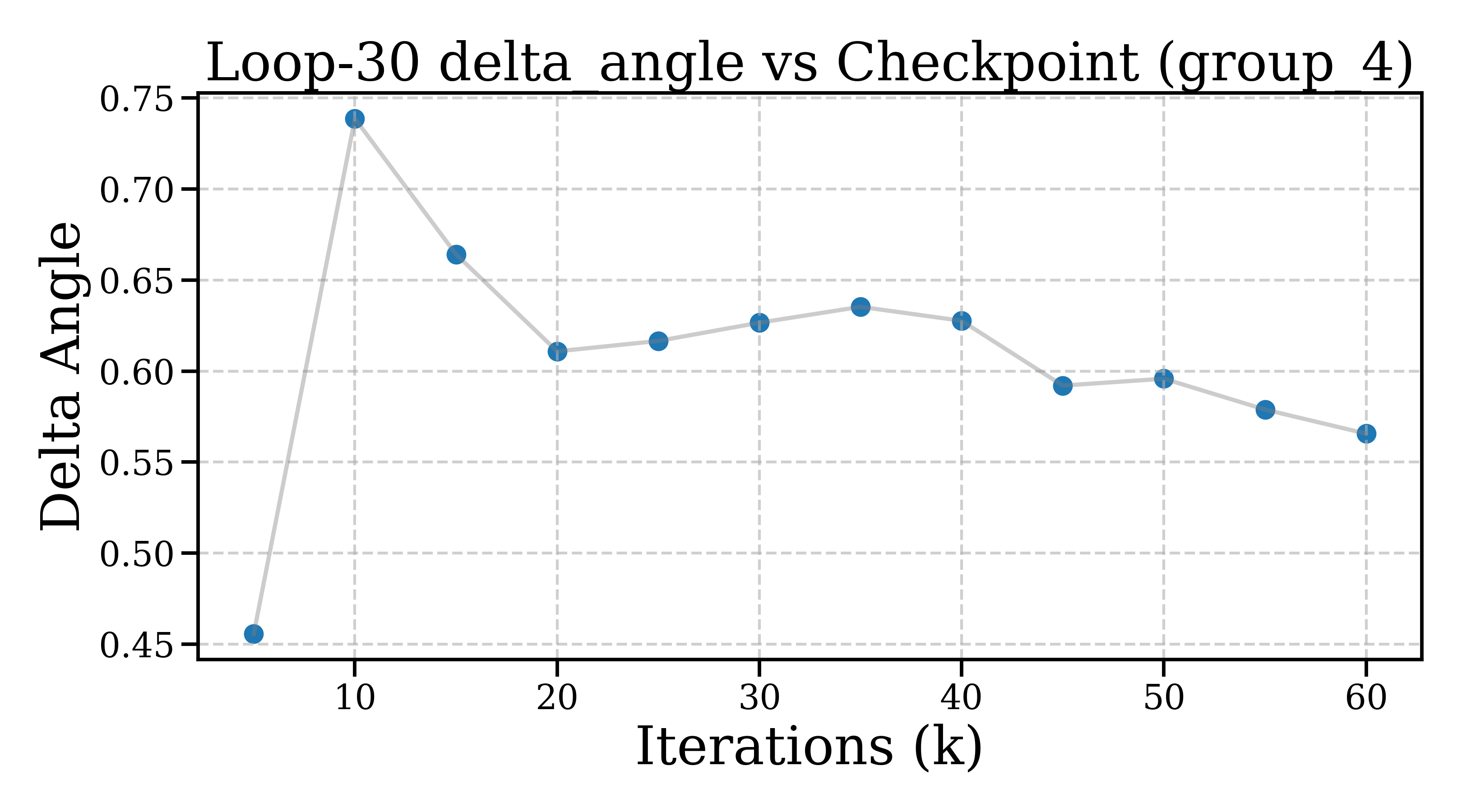
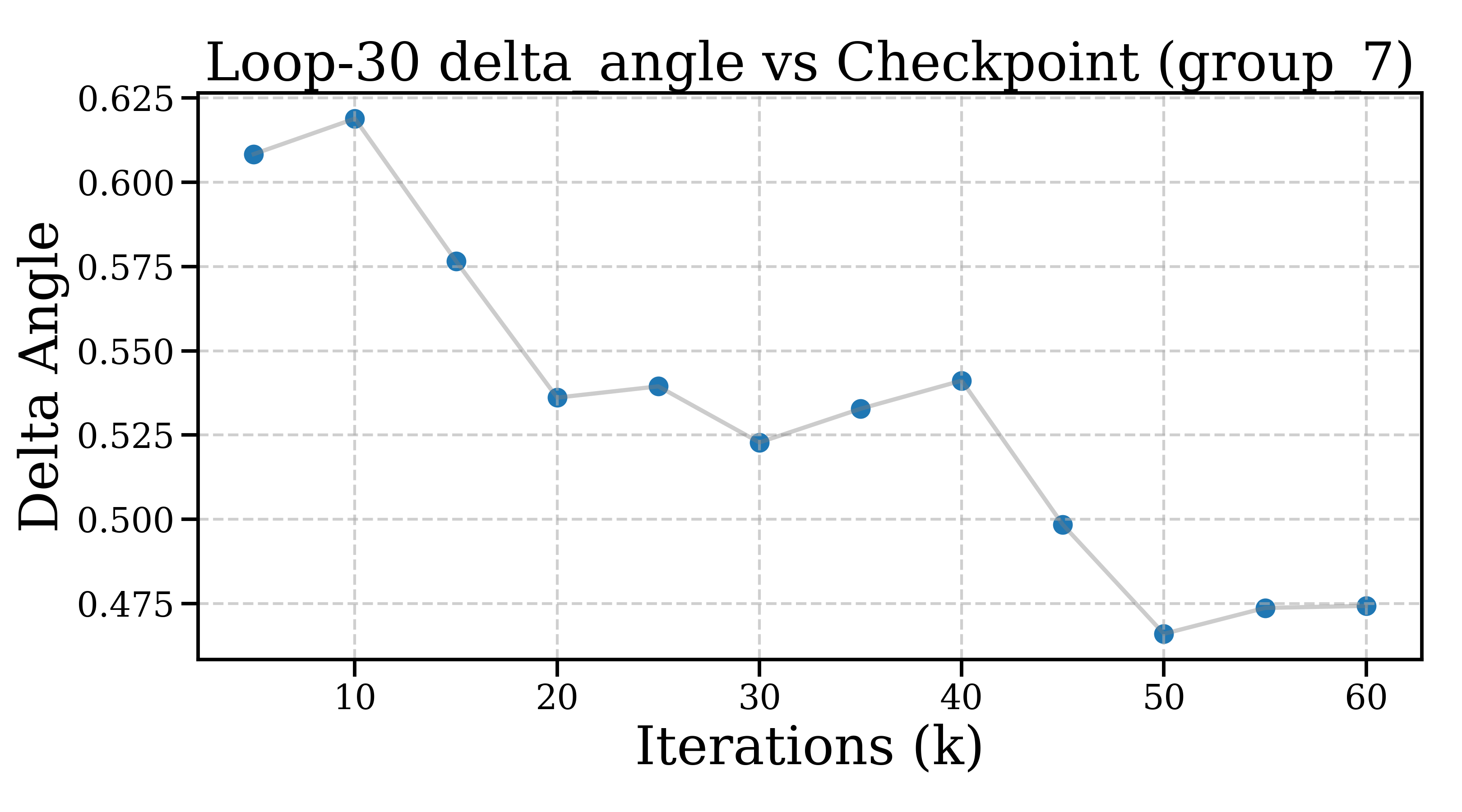
- Step angle: How different is the direction of the new change from the previous one? (Are you pushing in the same direction as before, or turning to refine from a new angle?)
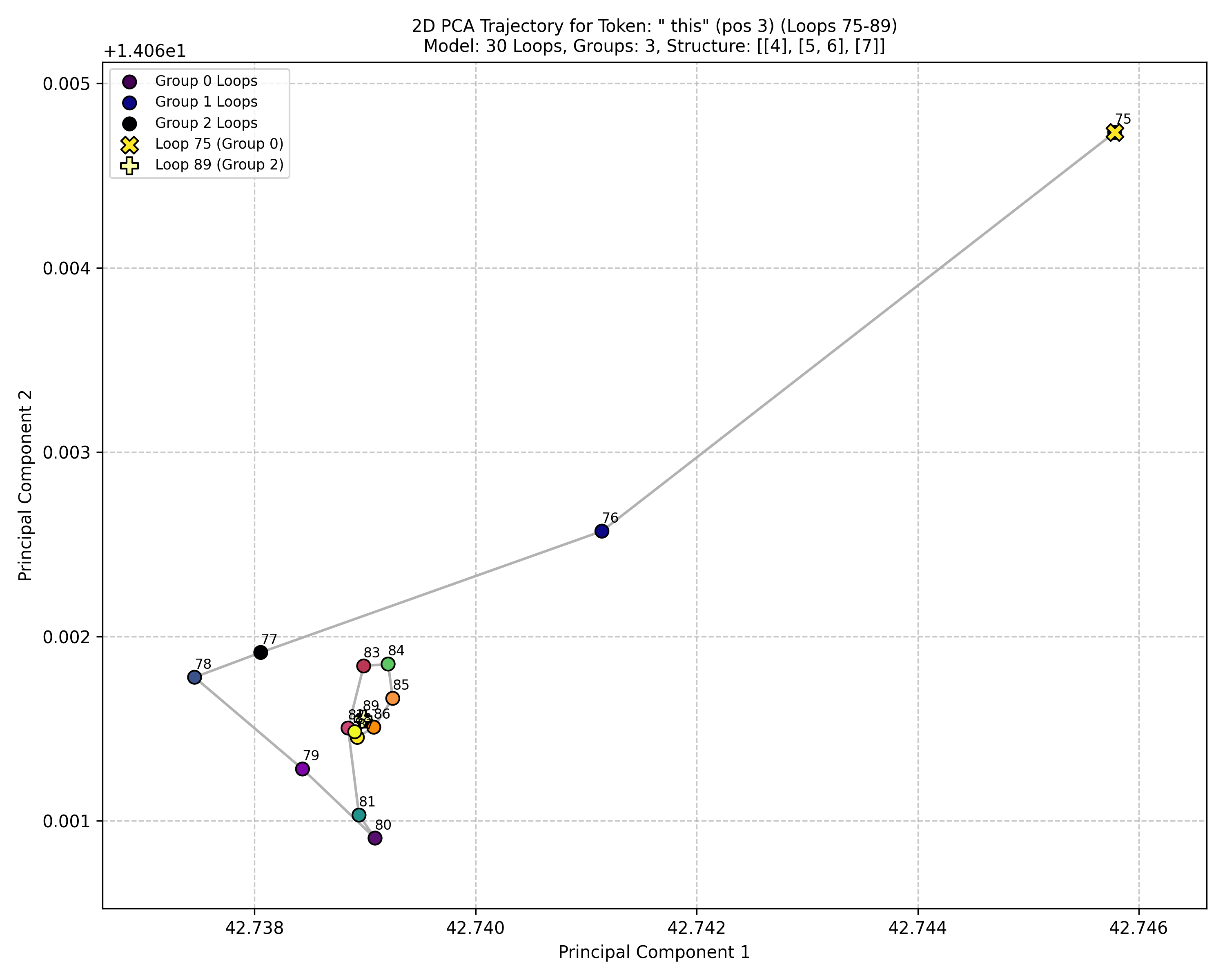
To visualize these movements, they used PCA, which is like flattening a 3D object into a 2D map so you can see the path. On this map, they looked at the path the hidden state takes as the model loops (thinks) and as it moves from one layer to the next.
They also tested three “early-exit” rules—ways to decide when to stop looping:
- Step size rule: Stop when the changes get small. Analogy: stop walking when your steps become tiny.
- KL rule: Stop when the model’s predicted word probabilities stop changing much. Analogy: stop when your final answer stops wobbling.
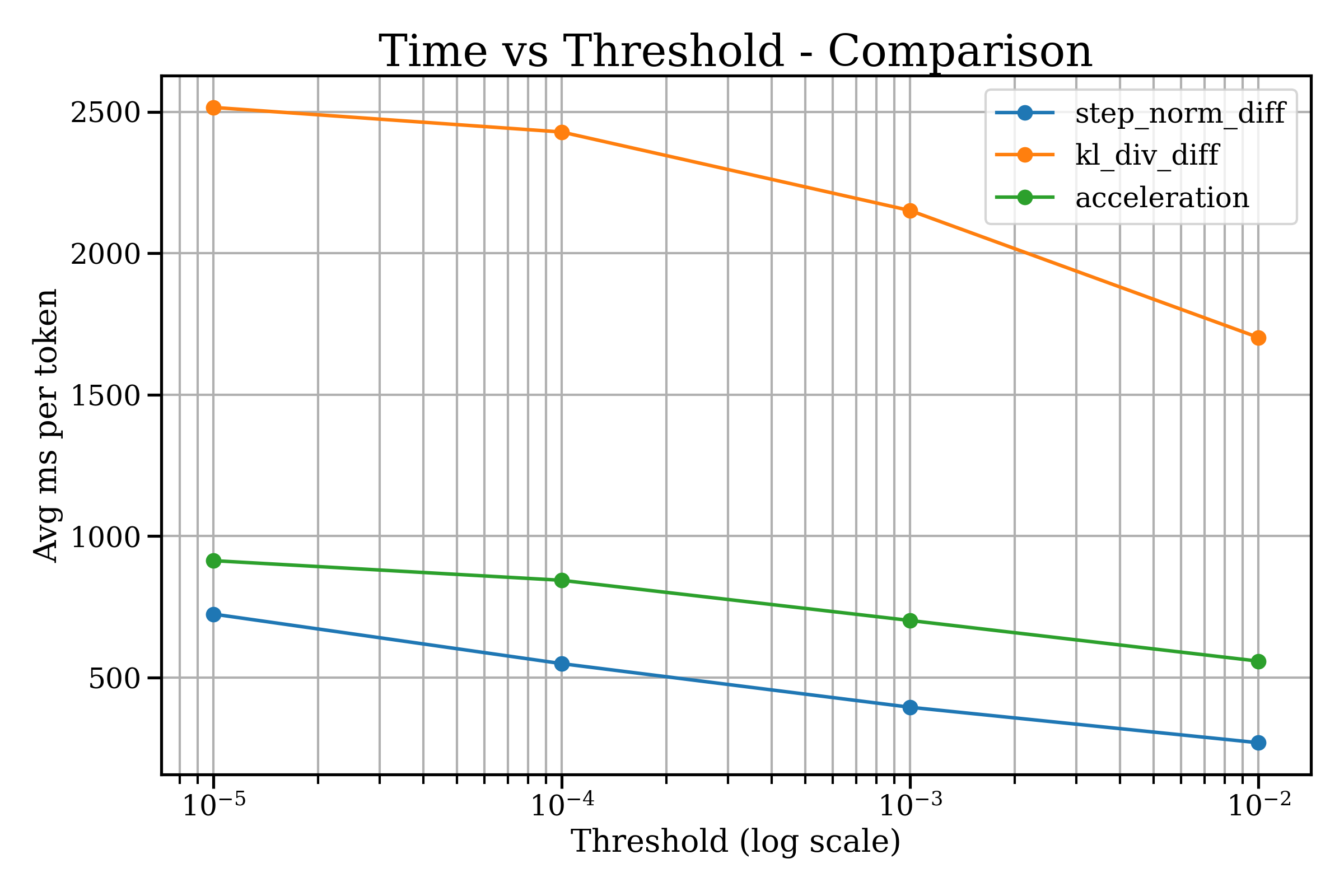
- Acceleration rule (their new method): Stop when the change between two steps’ updates becomes small. Analogy: stop when you’ve stopped turning the steering wheel—your refinements have settled into a smooth, steady path.
What did they discover, and why is it important?
They found a clear two-scale pattern:
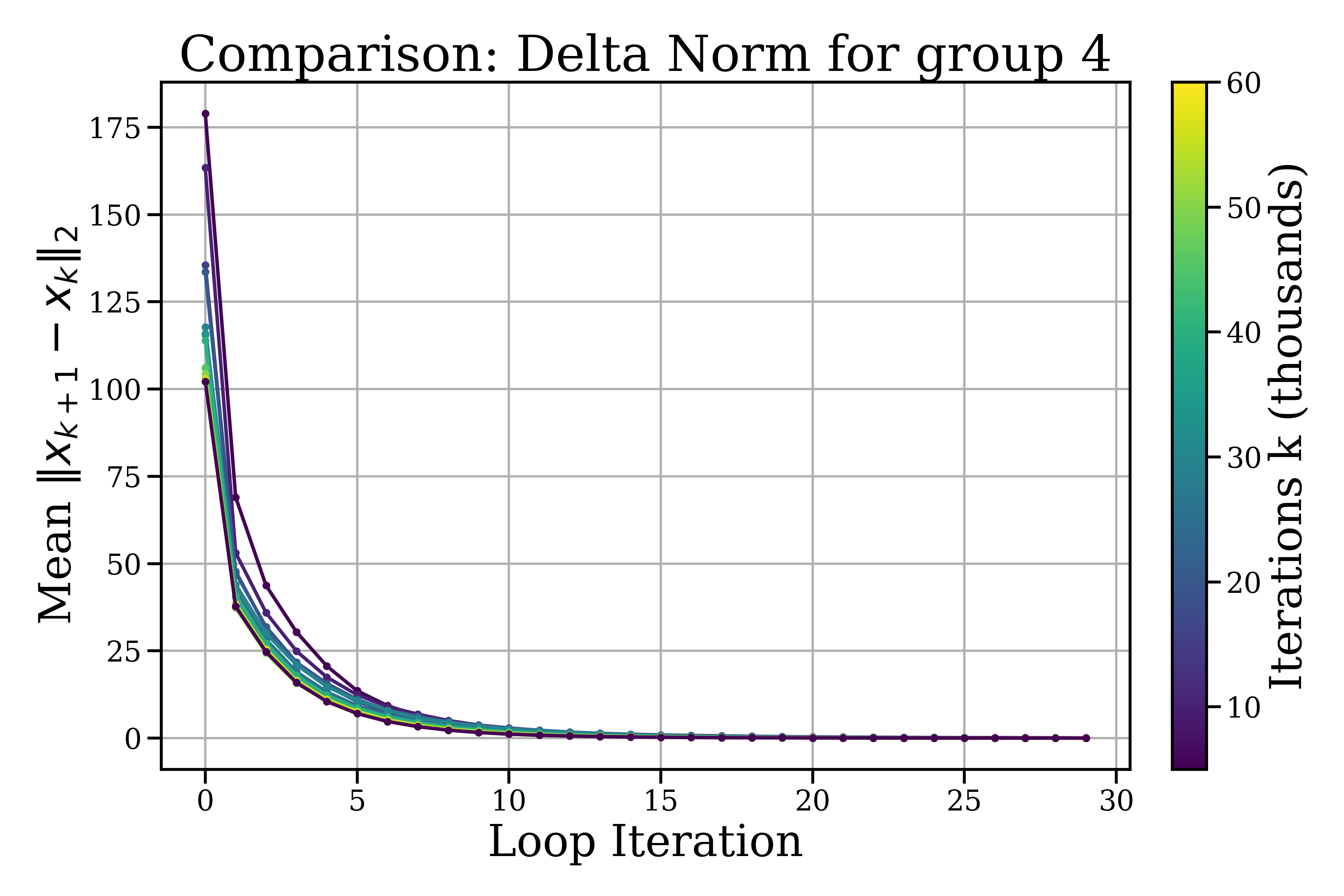
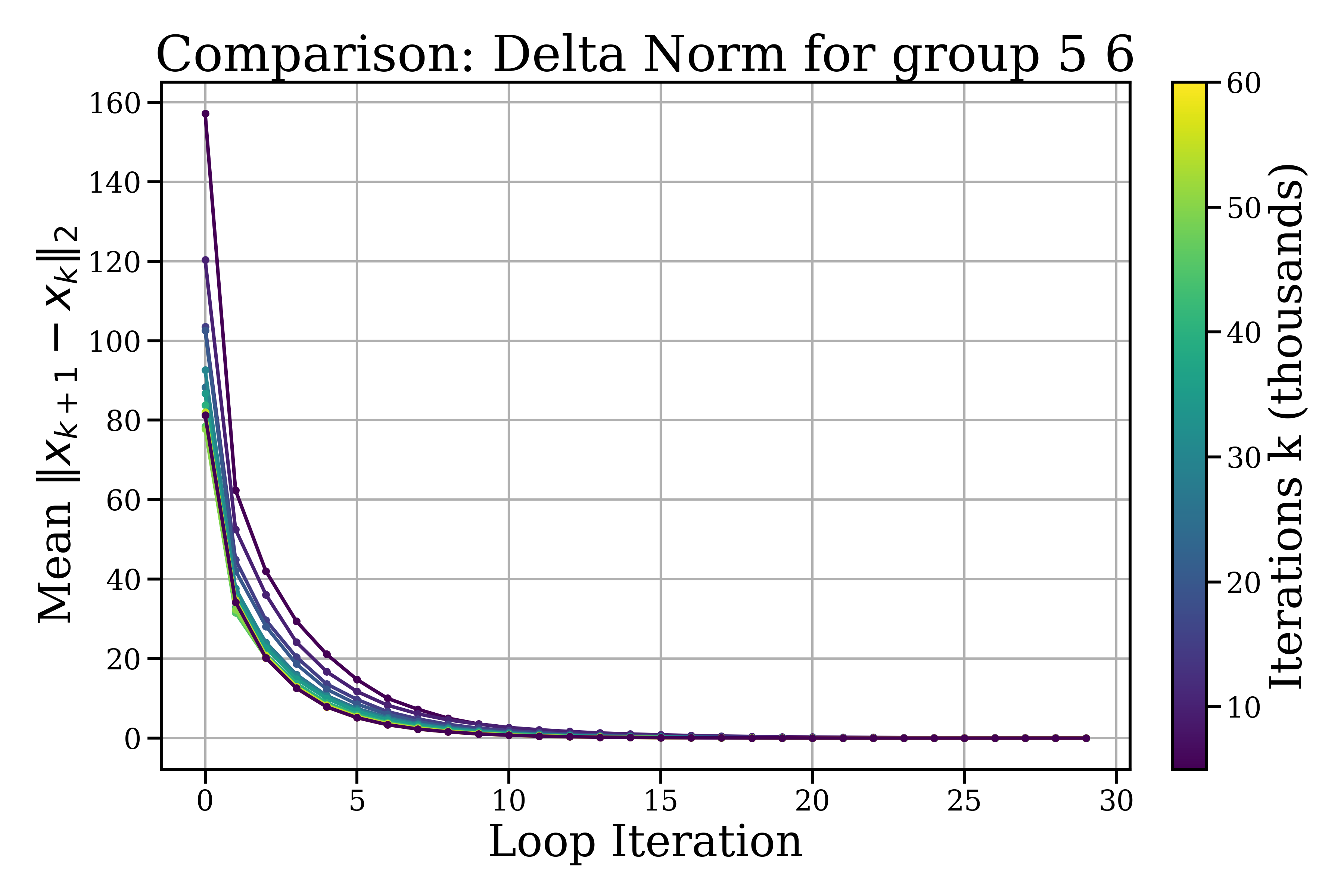
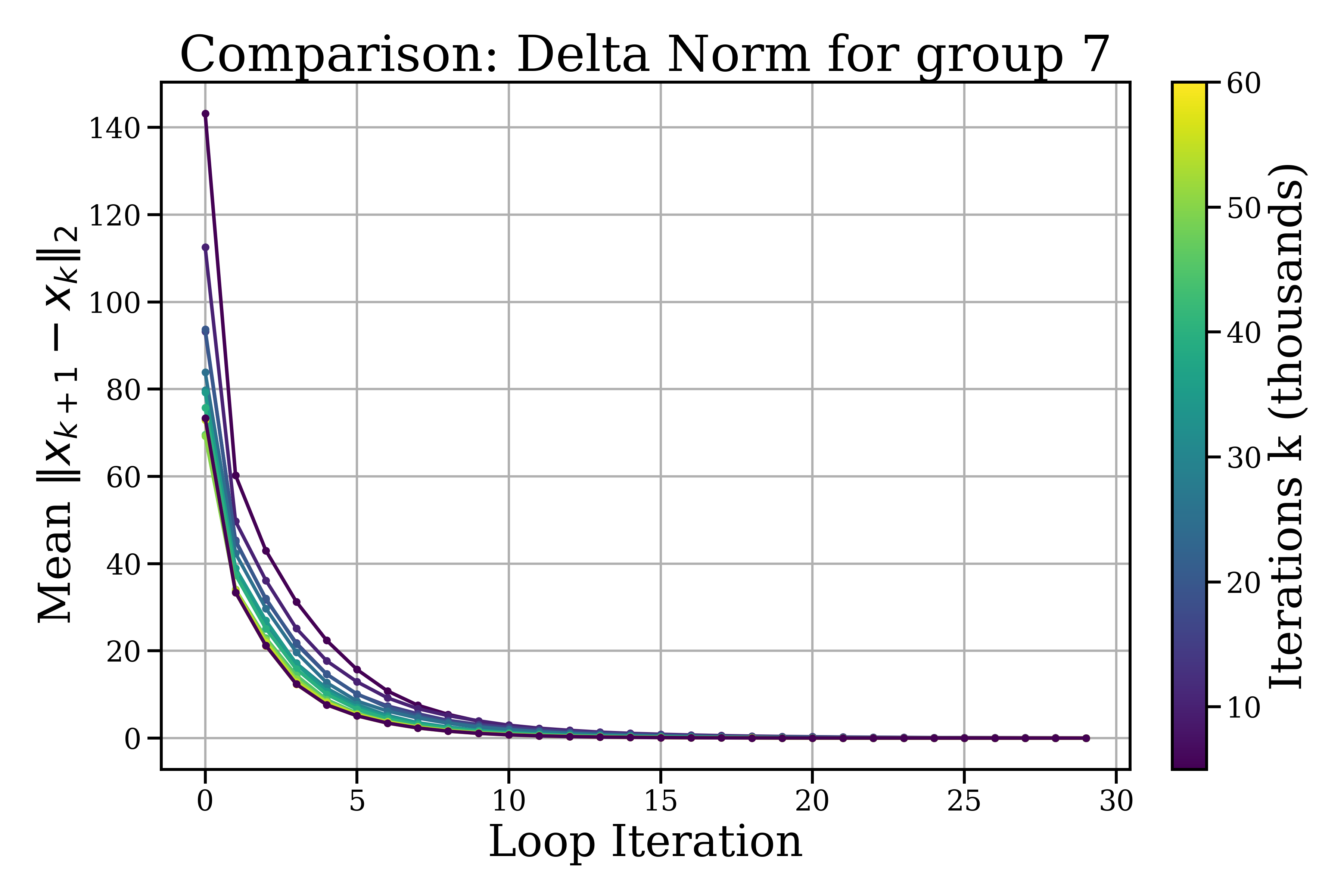
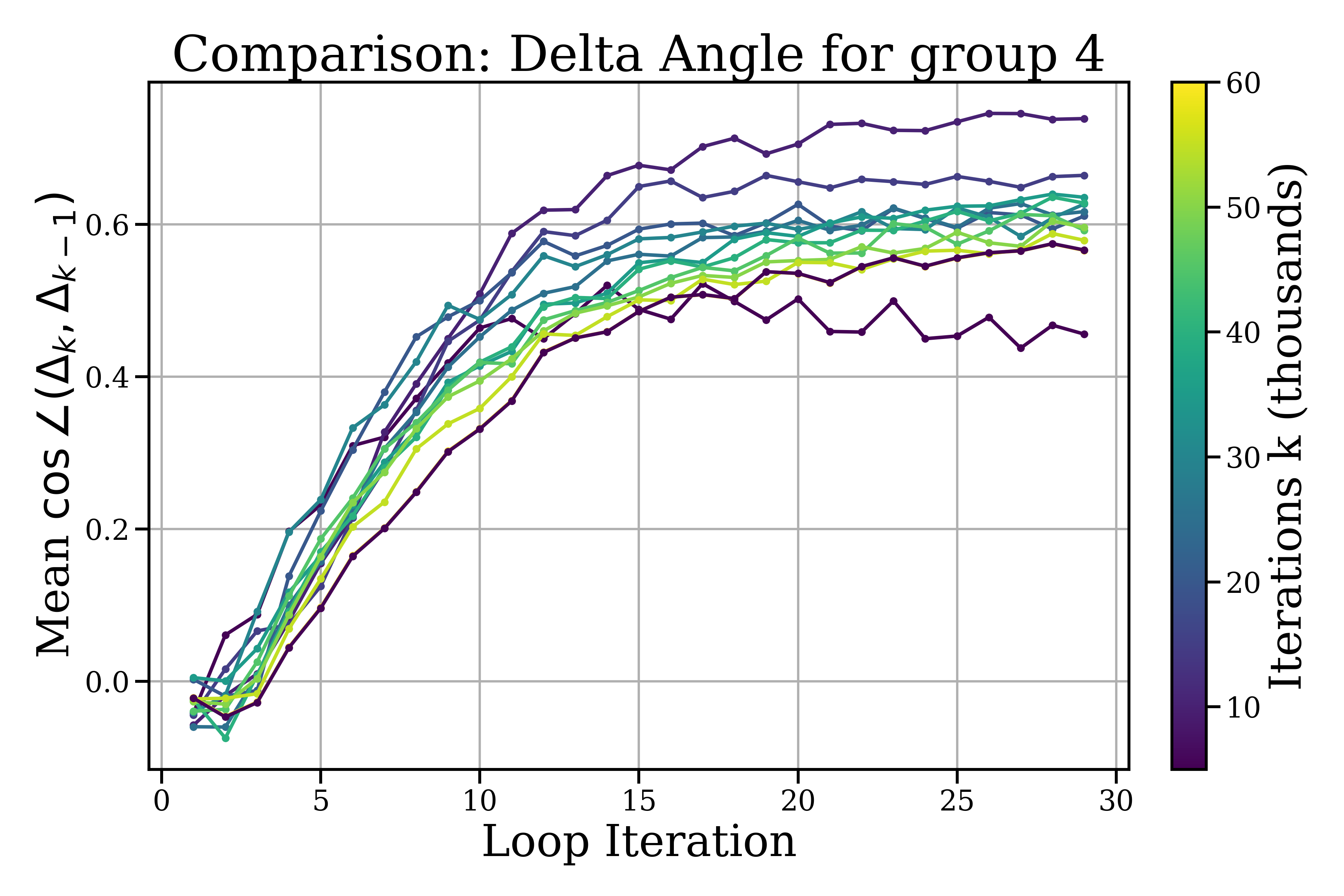
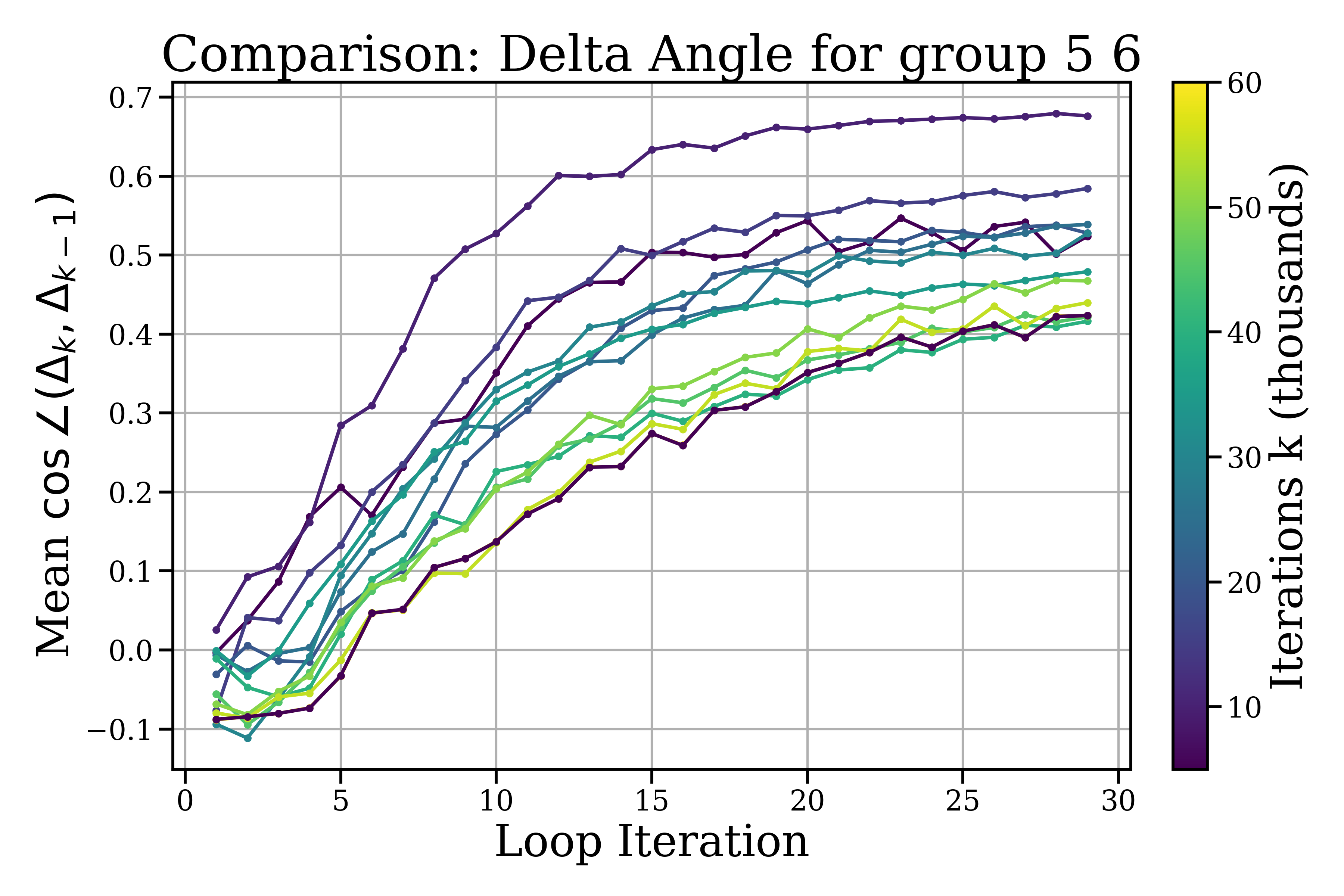
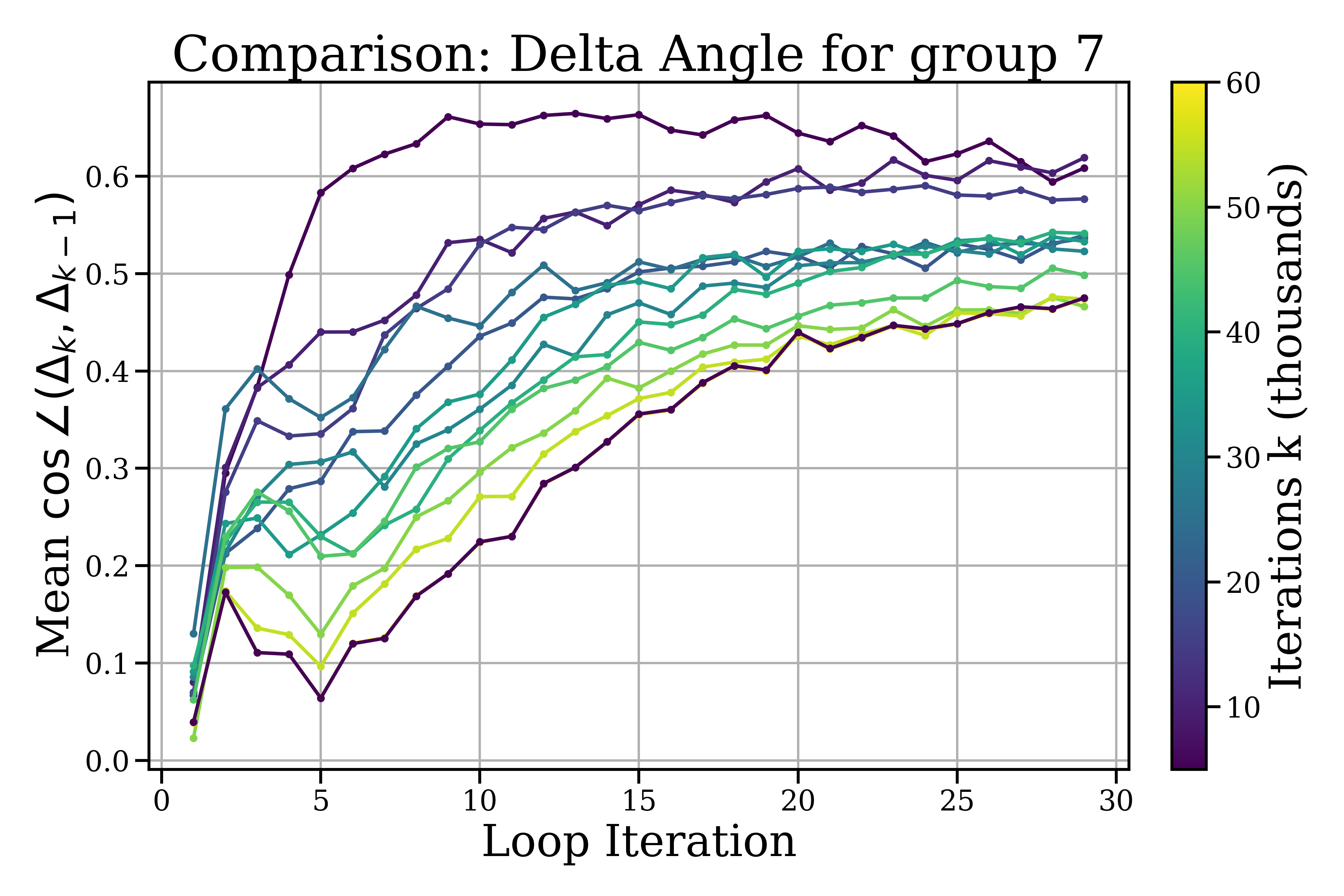
- Inside a looped block: the model makes small, quick refinements that soon level off and change directions more than they shrink—like tracing a neat spiral around a “good” idea. Steps get smaller within about 5–10 loop steps, and each new step tends to turn instead of pushing in the exact same direction.
- Across different blocks: the model makes bigger, coarser moves—like moving to a new area before doing fine polishing again.
Why this matters:
- The usual “stop when steps are small” rule can fail during spirals: the speed might be small but the direction is still changing, so you might stop too early or too late.
- The “KL” rule is stable but slow because it needs expensive calculations over the whole vocabulary.
- Their new “acceleration” rule detects when the spiral stabilizes—when updates stop changing—so it exits at just the right time. It’s cheap to compute and doesn’t need decoding.
In tests on their GPT-2–like model:
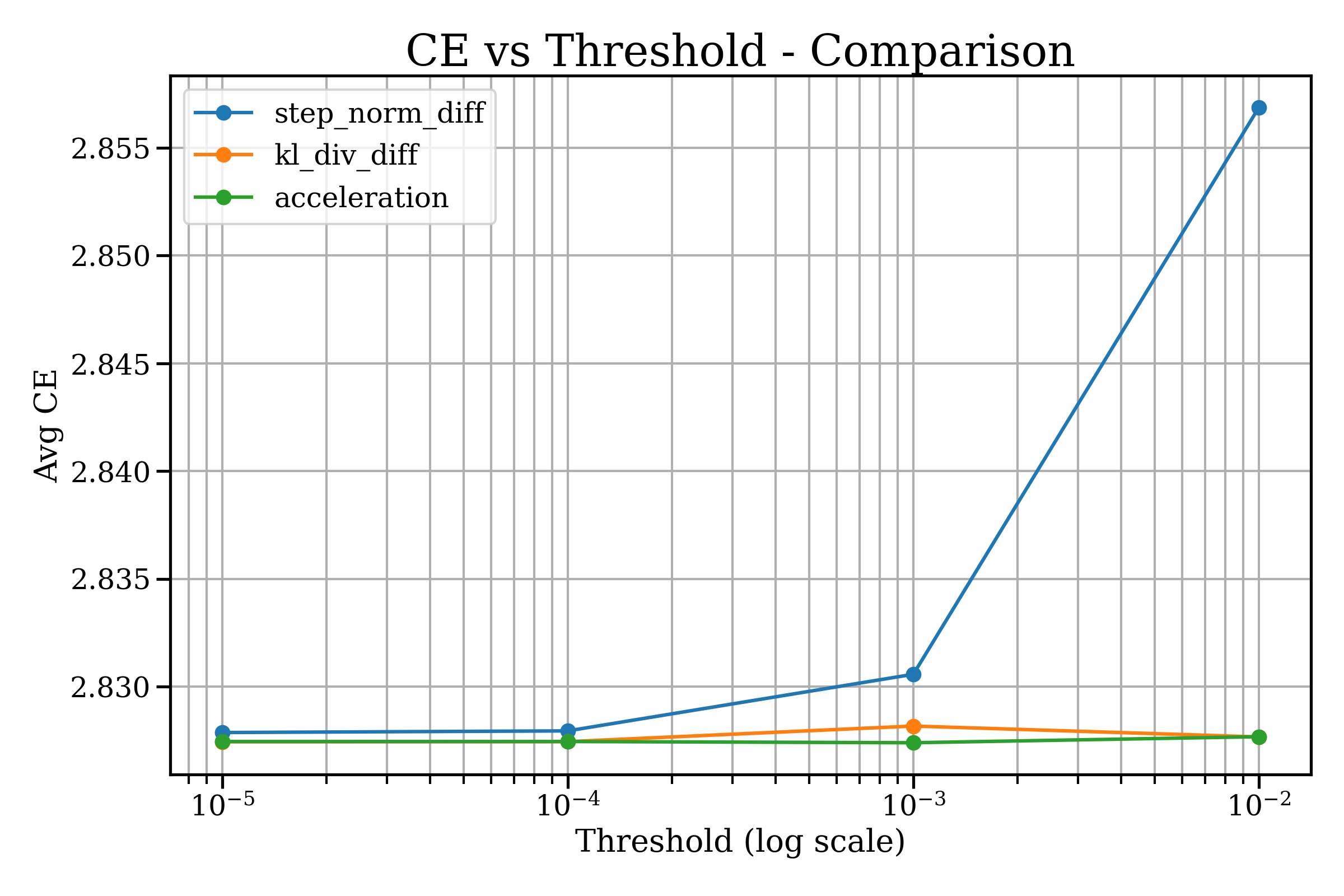
- The acceleration rule kept quality steady while cutting time noticeably (for example, roughly from about 580 ms/token to about 360 ms/token as the threshold was relaxed).
- The KL rule kept quality but was slower.
- The simple step-size rule was fast but could hurt quality if pushed too far.
Why does this matter? (Implications and impact)
This work shows a practical way to let LLMs think more internally—without flooding the conversation with extra text—while being smart about when to stop. The key idea is to use the geometry of the model’s own thinking:
- Small, turning steps inside loops mean “polishing.”
- Bigger jumps between blocks mean “major changes.”
By exiting when the polishing stops changing, you can keep answers accurate while making responses faster and cheaper. This could help:
- Everyday apps that need quick responses without long delays.
- Reasoning systems that benefit from extra internal thinking but must control latency.
- Future designs that dynamically choose how much “silent thinking” to do per token.
Limitations to keep in mind:
- The paper uses one mid-sized model and a specific looping setup.
- The analysis is based on observed behavior (not a formal proof) and uses 2D visualizations of very high-dimensional states.
- Results are averaged over many tokens, so individual cases may vary.
Still, the takeaway is simple and useful: looped layers do fine-tuning; deeper layers make bigger moves; and watching when fine-tuning stops changing gives a reliable, fast, and accurate stop signal.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of unresolved issues and concrete opportunities for further research raised by the paper’s methods, analyses, and claims.
- Generalization across architectures: Validate the two-scale geometry and the acceleration-based exit on diverse transformer backbones (e.g., LLaMA-style with rotary/ALiBi, deeper models, different normalization/activation schemes) to assess architecture sensitivity.
- Layer-position and recurrence-pattern ablations: Systematically vary which layers are looped (early vs mid vs late), the number of looped regions, and whether loops are paired or single to see how geometry and exit efficacy depend on recurrence placement.
- Mechanistic understanding of orthogonality: Provide a causal/mechanistic account of why loop updates become more orthogonal (e.g., roles of residual connections, attention vs MLP sublayers, normalization), beyond observational iterate statistics.
- Explicit geometric quantification: Measure discrete curvature/turning angles directly rather than inferring stabilization via the second-order difference; relate to formal curvature estimates, and test whether constant curvature produces low or high in practice.
- Link between latent geometry and prediction stability: Establish a theoretical and empirical mapping from latent acceleration to logit and probability stability (e.g., predict when low implies negligible changes in decoded distributions).
- Baseline breadth: Compare acceleration against additional early-exit strategies (e.g., entropy/confidence halting, ACT-style learned halting, mixture-of-depth gating, logit difference thresholds) to contextualize performance beyond step-norm and KL.
- Task-level evaluation: Assess latency–quality trade-offs on reasoning-heavy benchmarks (math, code, multi-step QA), calibration metrics, and generation quality—perplexity/CE alone may not predict reasoning gains or hallucination rates.
- Robustness to domain shift: Examine behavior under out-of-distribution inputs, adversarial or noisy prompts, and different languages/domains to identify failure modes of geometry-based exits.
- Token-level heterogeneity: Replace mean-over-tokens reporting with distributional analyses (tails, quantiles) and token-conditioned diagnostics (e.g., content vs function words, rare vs frequent tokens) to understand who benefits or suffers from early exit.
- Coordination across recurrent groups: Study policies that jointly coordinate exits across multiple looped blocks (e.g., global vs per-block controllers, dependencies when one group exits early and others continue).
- Threshold calibration: Develop and evaluate automatic or learned thresholding (per-block/per-token) and thoroughly test normalized variants (e.g., ) rather than suggesting them as “drop-in replacements” without empirical validation.
- Sensitivity to noise injection and looped-input projection: Ablate the recurrent input projection and injected noise to quantify their impact on loop geometry and exit stability; determine whether the observed spiral dynamics depend on these design choices.
- Long-loop behavior and stability: Characterize dynamics for large (e.g., oscillations, limit cycles, divergence), and identify safeguard conditions where acceleration exit may mis-halt under persistent rotation or slow directional drift.
- Training-time integration: Explore jointly training the model with a geometry-aware halting policy (e.g., RL or auxiliary losses encouraging stable-curvature loops) and examine whether such training changes the observed latent dynamics.
- Cross-token effects and TTC allocation: Analyze how early exit for one token influences future tokens via attention; design token-level TTC controllers that balance per-token exits with sequence-level performance.
- Projection artifacts: Go beyond 2D PCA (e.g., higher-dimensional embeddings, manifold learning, geodesic curvature) to ensure the visual “tight arcs” are not projection distortions; report reconstruction error or variance explained.
- Statistical rigor: Provide confidence intervals and significance tests for step norms/angles across checkpoints; resolve wording inconsistencies (e.g., “angles rise and settle at lower levels”) and precisely define “orthogonality” vs moderate cosine values (0.5–0.65).
- Hardware and deployment realism: Report latency across hardware types, batch sizes, and sequence lengths; include memory overhead (storing prior deltas), KV-cache interaction, and throughput under practical serving constraints.
- Failure-mode catalog for acceleration: Identify cases where becomes small while semantics/logits still change (e.g., slow rotations, small-amplitude but semantically impactful updates) and propose mitigations (multi-signal exits, angle thresholds).
- Broader safety and reliability impacts: Test whether earlier halting increases hallucination or reduces factuality; quantify rare catastrophic errors vs average-case gains to inform deployment risk profiles.
Practical Applications
Immediate Applications
The following items translate the paper’s findings into deployable use cases, with sectors, likely tools/workflows, and feasibility notes.
- Acceleration-based early exit in LLM inference servers — deploy the “two-hit” second-order exit rule to cut latency and cost while preserving quality; replaces KL-based exits that require vocab decoding.
- Sector(s): software/cloud, developer tools
- Tools/products/workflows: plugin for Hugging Face/Transformers, vLLM/Triton/TensorRT inference; PyTorch module that computes a(k)=||Δ(k)−Δ(k−1)||₂ with optional normalized variant; API to set τ per block/group
- Assumptions/dependencies: model must expose looped/recurrent blocks; per-block scaling may require normalized acceleration; thresholds require light calibration; tested at GPT‑2 scale—porting to larger models needs validation
- SLA-aware compute governance for production LLMs — use acceleration thresholds to meet per-request latency SLOs and reduce variance without degrading perplexity/cross-entropy.
- Sector(s): cloud operations, MLOps
- Tools/products/workflows: “Compute Governor” microservice that monitors latent updates and enforces exits; dashboards for ms/token, PPL/CE stability over τ; autoscaling policies tied to exit aggressiveness
- Assumptions/dependencies: telemetry from hidden states during inference; safe fallback when acceleration signal is noisy; alignment with autoscaling and batching strategies
- On-device assistants and offline/cellular-constrained LLMs — reduce battery drain and response time by exiting loops when curvature stabilizes instead of decoding KL every step.
- Sector(s): mobile, embedded/edge AI
- Tools/products/workflows: lightweight runtime with O(d) exit logic; “fast vs thorough” UI slider mapped to τ; per-model pre-calibrated τ tables
- Assumptions/dependencies: device models must support recurrent depth; small hidden sizes benefit most; local calibration to avoid premature exit under distribution shift
- Real-time voice/chat agents (contact centers, productivity copilot) — faster token streaming via latent halting, improving user experience without sacrificing answer quality.
- Sector(s): customer support, productivity software
- Tools/products/workflows: streaming inference with acceleration exit; UX controls for dynamic TTC; A/B harness comparing KL vs acceleration Pareto
- Assumptions/dependencies: tasks tolerant to minor logit rotations; guardrails to detect quality cliffs if τ too high
- Cost and energy optimization — lower power and carbon per token by avoiding expensive softmax/KL exit logic and trimming unnecessary loop steps.
- Sector(s): energy, sustainability reporting, cloud FinOps
- Tools/products/workflows: per-request energy accounting; “green mode” that raises τ when datacenter load is high; carbon dashboards tied to loop geometry metrics
- Assumptions/dependencies: measurable energy consumption at inference; organizational buy-in for dynamic quality/latency trade-offs
- Geometry diagnostics for model training and health — track step norms and consecutive-step angles to detect healthy “spiral” refinement vs pathological dynamics.
- Sector(s): MLOps, research/academia
- Tools/products/workflows: training/inference dashboards plotting ||Δ||₂ decay and cos∠(Δ(k),Δ(k−1)); alerts when angles fail to stabilize or norms don’t decay in 5–10 steps
- Assumptions/dependencies: access to intermediate states; PCA is illustrative but not necessary for thresholds; token-averaged statistics may hide outliers
- RAG and tool-use pipelines — allocate TTC to latent thinking instead of longer chain-of-thought tokens, exiting early when updates stop accelerating.
- Sector(s): enterprise search, knowledge management
- Tools/products/workflows: controller that prioritizes recurrent refinement before retrieval or tool calls; τ tuned per stage (reasoning vs retrieval)
- Assumptions/dependencies: pipeline supports recurrent-depth models; careful τ to avoid cutting reasoning for hard queries
- Robotics/high-frequency decision loops with LLM planners — accelerate internal reasoning for language-conditioned planning while keeping reaction times low.
- Sector(s): robotics, autonomous systems
- Tools/products/workflows: ROS node integrating acceleration exit; latency-aware controller switching τ based on task urgency
- Assumptions/dependencies: planner uses a recurrent-depth language module; safety review for premature halts under distribution shift
- Developer UX in IDE code assistants — smoother autocompletion by halting latent loops as soon as updates stabilize, reducing keystroke-to-token latency.
- Sector(s): developer tools
- Tools/products/workflows: IDE plugin runtime with acceleration exit; per-language τ presets; telemetry for token timing
- Assumptions/dependencies: code LLM supports looped blocks; balance τ against hallucination risks for longer completions
- Compliance and safety guardrails — exit loops early when geometry suggests stable local curvature to reduce degenerate oscillations or saturation states.
- Sector(s): AI safety, governance
- Tools/products/workflows: guardrail that detects abnormal angle/norm patterns; auto-fallback to conservative τ; logging for audit
- Assumptions/dependencies: thresholds defined with risk teams; monitoring for adversarial prompts that affect latent geometry
Long-Term Applications
These items are promising but need further research, scaling, or ecosystem development.
- Adaptive per-block, per-token compute controllers — learn τ policies that vary across blocks and tokens using reinforcement learning or bandit strategies.
- Sector(s): software/cloud, research
- Tools/products/workflows: “Mixture-of-Depths” + acceleration hybrid controller; τ schedulers conditioned on hidden states; meta-learning of exit policies
- Assumptions/dependencies: training data for controllers; safe exploration; generalization across tasks/models
- Hybrid latent-vs-token reasoning schedulers — dynamically choose between extra latent loops and emitting more chain-of-thought tokens based on geometry signals.
- Sector(s): productivity apps, education, healthcare triage
- Tools/products/workflows: policy that uses acceleration to decide “think more” vs “say more”; task-aware heuristics and cost models
- Assumptions/dependencies: robust mapping from geometry to downstream task value; user experience tuning
- Scaling to frontier models and multimodal systems — extend two-scale dynamics and acceleration exits to larger LLMs and VLMs with vision/audio blocks.
- Sector(s): multimodal AI, robotics, media
- Tools/products/workflows: generalized exit kernels for cross-modal hidden states; angle/norm measures in non-text embeddings
- Assumptions/dependencies: confirm similar spiral/drift geometry in larger/multimodal models; hardware-friendly implementations
- Latent-space interpretability and auditing — use step norms/angles to visualize fine-grained refinement vs cross-block drift for transparency and debugging.
- Sector(s): AI governance, academia
- Tools/products/workflows: “Latent Trace Explorer” that reconstructs token trajectories; audit reports correlating geometry with decision changes
- Assumptions/dependencies: reliable mappings from geometry to semantic changes; privacy-safe access to latents
- Hardware-software co-design — add primitives to accelerators for cheap Δ and acceleration computations, enabling geometry-aware exits at line rate.
- Sector(s): semiconductors, AI hardware
- Tools/products/workflows: fused vector diff and norm ops; memory layouts optimized for recurrent blocks; firmware APIs for τ control
- Assumptions/dependencies: vendor adoption; measurable latency gains over CPU/GPU baselines
- Standardization of geometry-based TTC reporting — policy frameworks for measuring and disclosing dynamic compute use and energy via latent metrics.
- Sector(s): policy/regulation, sustainability
- Tools/products/workflows: reporting standards for ms/token, energy/token, and halting triggers; compliance dashboards
- Assumptions/dependencies: consensus on metrics; reproducibility across vendors; privacy considerations
- Robustness under distribution shift — certify that acceleration exits maintain quality for rare or adversarial inputs, and design safeguards when spiral dynamics break.
- Sector(s): AI safety, finance, healthcare
- Tools/products/workflows: stress-testing suites for exit stability; anomaly detectors for angle/norm regimes; fallback to KL/entropy-based exits
- Assumptions/dependencies: labeled edge-case datasets; clear failure modes; layered defense design
- Curriculum and training objectives that encourage healthy loop geometry — train models to develop small, orthogonal refinements and stable curvature for reliable exits.
- Sector(s): academia, model training
- Tools/products/workflows: geometry-aware regularizers; loop-sampling schedules; per-block halting supervision
- Assumptions/dependencies: scalability to large datasets; compatibility with standard optimizers
- Cross-layer coordination strategies — exploit slow drift across blocks by distributing τ budgets strategically (e.g., aggressive halting in early loops, conservative later).
- Sector(s): inference systems, research
- Tools/products/workflows: block-wise τ planners; learned block importance weights; runtime profiling
- Assumptions/dependencies: validated two-scale separation across architectures; controller training
- Concurrent serving and auto-batching — use geometry exits to release tokens early and improve concurrency, reducing tail latency in multi-tenant systems.
- Sector(s): cloud platforms
- Tools/products/workflows: schedulers that reassign compute when tokens halt; queueing models aware of variable loop lengths
- Assumptions/dependencies: integration with batching frameworks; fairness policies to avoid starvation
Notes on Assumptions and Dependencies (applies broadly)
- The paper’s evidence is observational on a GPT‑2–like model and specific recurrence pattern; generalization to larger/frontier models requires empirical validation.
- Successful deployment requires models with recurrent-depth blocks and access to intermediate states; standard one-pass Transformers need modification.
- Acceleration is O(d) per token-step and sensitive to latent scaling; normalized forms mitigate scale variance across blocks/models.
- Threshold τ selection is simpler than KL but still needs light calibration; two-hit checks reduce spurious exits.
- PCA visualizations are illustrative; production exits should rely on iterate-only signals (norms/angles/acceleration) rather than 2D projections.
- Task-specific sensitivity (e.g., finance/healthcare) may demand conservative τ and fallback exits (KL/entropy) under detected anomalies.
Glossary
- Acceleration: The second-order difference in consecutive loop updates, used as a curvature-sensitive signal to decide when to halt. "Acceleration (ours):"
- Adaptive Computation Time (ACT): A mechanism that lets a model dynamically decide how many computation steps to use by learning a halting policy. "Universal Transformers share parameters across depth and learn to halt (often via ACT)"
- ALiBi: Attention with Linear Biases; a positional bias technique for Transformers that avoids explicit positional embeddings. "learned positional embeddings (no ALiBi/rotary)"
- Angular refinement: The stabilization of the angle between consecutive updates, indicating non-collinear, refinement-like adjustments within a loop. "angular refinement, the stabilization of indicating non-collinear, refinement-like updates."
- Chain-of-thought: A prompting and generation style where models produce intermediate reasoning steps as text to improve problem-solving. "chain-of-thought and deliberation systems"
- Cross-entropy (CE): A standard loss/metric measuring divergence between predicted and true distributions; used here to assess quality. "Quality is perplexity (PPL) and cross-entropy (CE) on held-out text."
- Decoder-only transformer: A Transformer architecture that uses only the decoder stack, typical of autoregressive LLMs. "GPT-2-style decoder-only transformer"
- Early exit: A strategy to halt recurrent or depth iterations during inference when a stopping criterion is met to save compute. "Geometry-inspired early exit and trade-offs"
- Entropy: A measure of uncertainty in a probability distribution, often used for adaptive halting heuristics. "entropy/confidence heuristics"
- FLOPs: Floating-point operations; a measure of computational cost used to quantify test-time compute. "so that extra FLOPs improve the representation rather than the sequence length."
- GPT-2: A widely used decoder-only LLM architecture referenced as the backbone in experiments. "a GPT-2–like model"
- Hidden state: The latent representation vector maintained and updated across model layers/loops. "initial hidden state "
- KL-divergence: A divergence metric between probability distributions used here to detect stabilization of decoded outputs. "KL-divergence exit strategy of Geiping et al."
- Latency-quality Pareto: The trade-off frontier showing how inference latency and output quality balance across exit policies. "delivering a better latency-quality Pareto than step-norm and KL-based baselines."
- Latent space: The internal representational space in which the model performs refinements before emitting tokens. "A complementary option is to think in latent space"
- Logits: Pre-softmax scores output by a model that determine the predicted distribution over tokens. "reacts later when small latent rotations still change logits."
- Lognormal-Poisson schedule: A sampling scheme used to draw loop iteration counts during training. "lognormal-Poisson schedule defined by \citet{geiping2025scaling}"
- Looped-input projection: A technique to project and re-feed hidden states back into a block when applying it recurrently. "we use the looped-input projection technique of~\citet{geiping2025scaling}."
- Orthogonality: The geometric property of consecutive updates having low cosine similarity, indicating direction changes rather than collinear pushes. "step orthogonality "
- PCA: Principal Component Analysis; a dimensionality reduction method used to visualize latent trajectories. "visualized with PCA trajectories."
- Perplexity (PPL): A standard LLMing metric indicating how well the model predicts text; lower is better. "Quality is perplexity (PPL) and cross-entropy (CE) on held-out text."
- Positional embeddings: Learned vectors that encode token positions in a sequence for attention. "learned positional embeddings (no ALiBi/rotary)"
- Radial refinement: The rapid decay of update norms within loop steps, indicating smaller, fine-grained adjustments. "radial refinement, the rapid decay of within a small number of loop steps;"
- Recurrent depth: Iterating Transformer blocks multiple times at inference to perform additional latent computation per token. "Recurrent-depth transformers scale test-time compute by iterating latent computations before emitting tokens."
- RMSnorm: Root Mean Square Layer Normalization; an alternative normalization technique used in the model. "sandwhich normalization (using RMSnorm)"
- Rotary: Rotary positional embeddings; a method to encode relative positions via rotation in embedding space. "learned positional embeddings (no ALiBi/rotary)"
- Second-order exit criterion: A halting rule based on the change in the update (acceleration) rather than the update norm itself. "A second-order exit criterion that halts when consecutive updates stop changing"
- SiLU: Sigmoid Linear Unit; an activation function used in the network. "Nonlinearities are SiLU."
- Softmax: A function that converts logits into a probability distribution over the vocabulary. ""
- Step-norm: An exit rule that halts when the magnitude of the latent update falls below a threshold. "Step-norm (\citet{geiping2025scaling)}:"
- Test-time compute (TTC): The amount of computation spent during inference per token. "test-time compute (TTC)"
- Universal Transformers: A Transformer variant with shared parameters across layers and a learned halting mechanism. "Universal Transformers share parameters across depth and learn to halt (often via ACT)"
Collections
Sign up for free to add this paper to one or more collections.