Structured Sparse Transition Matrices to Enable State Tracking in State-Space Models (2509.22284v2)

Abstract: Modern state-space models (SSMs) often utilize transition matrices which enable efficient computation but pose restrictions on the model's expressivity, as measured in terms of the ability to emulate finite-state automata (FSA). While unstructured transition matrices are optimal in terms of expressivity, they come at a prohibitively high compute and memory cost even for moderate state sizes. We propose a structured sparse parametrization of transition matrices in SSMs that enables FSA state tracking with optimal state size and depth, while keeping the computational cost of the recurrence comparable to that of diagonal SSMs. Our method, PD-SSM, parametrizes the transition matrix as the product of a column one-hot matrix ($P$) and a complex-valued diagonal matrix ($D$). Consequently, the computational cost of parallel scans scales linearly with the state size. Theoretically, the model is BIBO-stable and can emulate any $N$-state FSA with one layer of dimension $N$ and a linear readout of size $N \times N$, significantly improving on all current structured SSM guarantees. Experimentally, the model significantly outperforms a wide collection of modern SSM variants on various FSA state tracking tasks. On multiclass time-series classification, the performance is comparable to that of neural controlled differential equations, a paradigm explicitly built for time-series analysis. Finally, we integrate PD-SSM into a hybrid Transformer-SSM architecture and demonstrate that the model can effectively track the states of a complex FSA in which transitions are encoded as a set of variable-length English sentences. The code is available at https://github.com/IBM/expressive-sparse-state-space-model

• The paper presents PD-SSM, which uses PD parametrization with a binary one-hot matrix and complex-valued diagonal matrix to enable efficient state tracking in SSMs.
• It demonstrates state-of-the-art performance in finite-state tracking tasks and multivariate time-series classification while reducing computational overhead.
• The model guarantees BIBO stability and integrates seamlessly into hybrid architectures, combining Transformer and SSM layers for improved long-range dependency handling.

Structured Sparse Transition Matrices to Enable State Tracking in State-Space Models

The paper introduces PD-SSM, a novel approach to enhance state-space models (SSMs) by employing structured sparse parametrization for transition matrices. This methodology promises improved expressivity without the computational burden typical of unstructured matrices, thus achieving efficient emulation of finite-state automata (FSA).

PD Parametrization

The central innovation is the PD parametrization, which represents the transition matrix as a product of a binary column-one-hot matrix $P$ and a complex-valued diagonal matrix $D$. The PD parametrization supports efficient computation through parallel scans and maintains bounded-input bounded-output (BIBO) stability due to the constraint $|D(u_t)| < 1$. This architecture can easily integrate into existing frameworks, allowing PD matrices to be utilized alongside traditional components of SSMs without the need for extensive modifications.

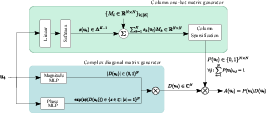
Figure 1: The PD parametrization can be integrated into any selective SSM by adopting the shown architecture for generation of structured sparse state transition matrices $A(u_t) = P(u_t) D(u_t)$.

Implementation and Performance

The implementation of PD-SSM is demonstrated through various benchmarks, highlighting its ability to handle complex FSAs efficiently. Notably, PD-SSM exhibits state-of-the-art performance in finite-state tracking tasks and competitive results in multivariate time-series classification. These results are achieved with reduced computational overhead compared to models using unstructured matrices.

The empirical analysis underscores PD-SSM's ability to generalize across varying sequence lengths, outperforming competing models like diagonal SSMs, especially on tasks involving tracking non-solvable automata within sequence lengths much larger than those seen during training.

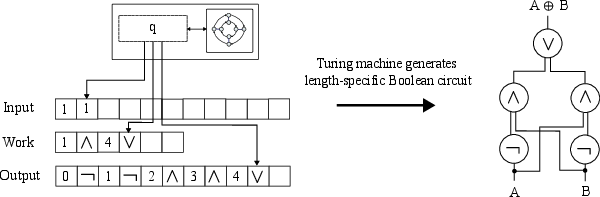
Figure 2: A visualization of a uniformly generated circuit family, with the specific example being the XOR circuit for inputs of length 2.

Stability and Expressivity

The paper theoretically proves that PD-SSM can emulate any $N$-state FSA with optimal state size and depth. The approach relies on PD matrices' algebraic properties, ensuring computational efficiency (linear scaling with state size) and maintaining system stability under finite precision. This blend of theoretical robustness and empirical efficacy positions PD-SSM as a compelling alternative for applications requiring precise state tracking in complex FSAs.

Applications and Future Work

As a scalable solution, PD-SSM is well-suited for integrating into hybrid architectures, such as combining Transformer and SSM layers, facilitating improved performance in tasks demanding long-range dependencies and expressive state modeling. Future research may explore further optimizations for PD matrix generation to enhance runtime efficiency even further, as well as the integration with large-scale AI pretraining paradigms.

Conclusion

PD-SSM provides a practical step forward in making state-space models more computationally feasible while retaining expressive power for emulating complex automata. The structured sparse transition matrices enable efficient state tracking, driving advancements in both theoretical understanding and empirical results in sequence modeling.

The ability to perform with high efficiency and expressivity marks PD-SSM as an essential tool in advancing sequence models' capabilities to handle complex tasks more effectively than traditional methods, opening pathways for further enhancements in AI architectures.