- The paper introduces CompreSSM, which compresses state space models during training by leveraging balanced truncation to reduce state dimensions and speed up optimization.
- It employs Hankel singular value analysis to quantify state importance, ensuring that essential dynamics are preserved while achieving computational efficiency.
- Empirical tests on datasets like MNIST and Long Range Arena demonstrate that the approach accelerates training and maintains model accuracy compared to traditional methods.
The Curious Case of In-Training Compression of State Space Models
The paper "The Curious Case of In-Training Compression of State Space Models" discusses the CompreSSM algorithm, which applies principles from control theory to in-training model compression in State Space Models (SSMs). The novel approach leverages balanced truncation techniques to achieve computational efficiency and maintain high expressivity in SSMs. This essay outlines the core concepts, the proposed pipeline, and the empirical validation of CompreSSM.
Introduction
State Space Models are gaining significance as they offer alternatives to RNNs and Transformers for sequence modeling tasks. They efficiently handle long sequences through recurrent dynamical systems that maintain hidden states. The computational challenge lies in balancing expressivity with the computational burden associated with state dimensions.
The paper proposes CompreSSM, a method that uses balanced truncation to reduce model order during training instead of post-training, significantly accelerating optimization while retaining performance. This approach is based on Hankel singular value analysis, a technique from control theory that measures state energy and facilitates state compression with guaranteed performance.
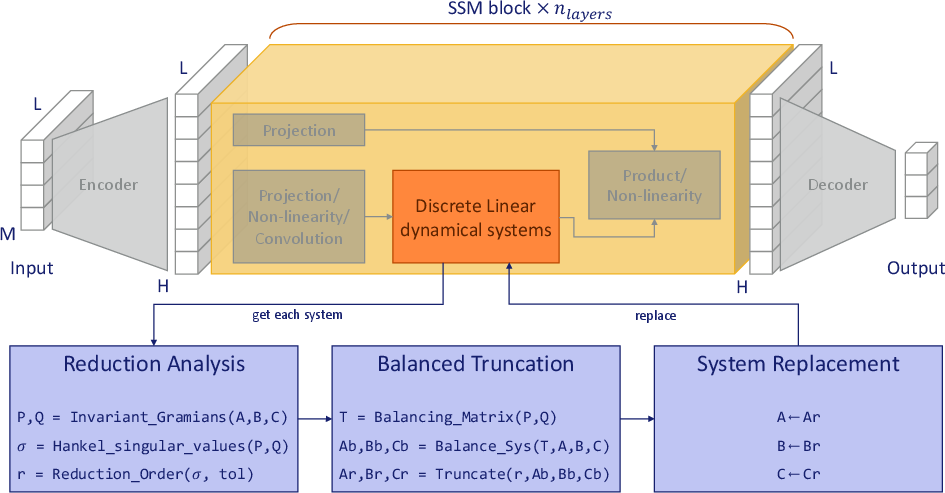
Figure 1: Overview of the proposed balanced truncation pipeline.
Mathematical Preliminaries
Discrete Linear Time-Invariant Systems
The mathematical framework of discrete Linear Time-Invariant (LTI) systems sets the foundation for applying control-theoretic techniques. An LTI system's state is updated incrementally, with matrices dictating dynamics. The pivotal role of Hankel singular values (HSVs) emerges in assessing the importance of state dimensions for input-output behavior.
Gramians and Balanced Realizations
Controllability and observability Gramians are quantitative measures indicating how states can be influenced by inputs and observed from outputs, respectively. An LTI system can be transformed into a balanced realization where these Gramians are identical and diagonal.
Balanced truncation exploits the ordering of HSVs to approximate systems while maintaining stability and bounding error. The reduced system retains the essential dynamics of its original state space representation, emphasizing performance efficiency.
The Proposed In-Training Reduction Scheme
CompreSSM: The Algorithm
CompreSSM systematically reduces state dimensions at early training stages by tracking HSVs. The algorithm proceeds block by block, extracting system matrices, solving Lyapunov equations for Gramians, computing HSVs, and truncating states based on predefined thresholds.
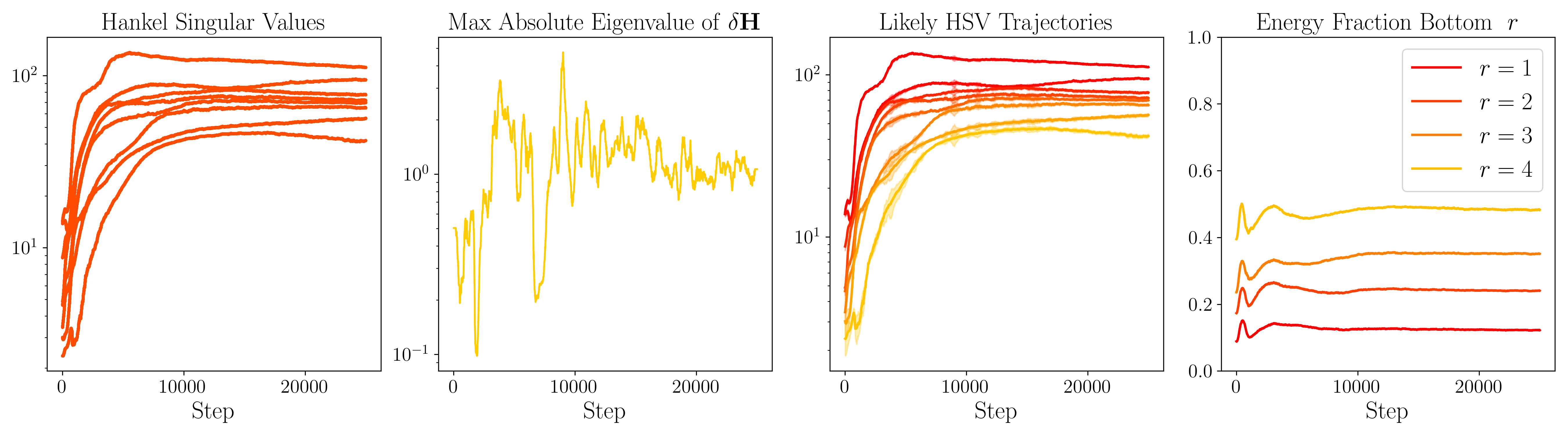
Figure 2: In-training per-step analysis of Hankel singular value dynamics.
Reductions are executed when improvements in training time and model performance warrant the process. The method's ability to apply in-training compression offers advantages over traditional post-training methods.
Justification and Empirical Evidence
The empirical results show that tracking HSV dynamics during training is feasible and reliable. Observations indicate stable ordering and contributions of HSVs, validating the approach's assumptions. The reductions facilitate training speed-up without compromising accuracy.
Experiments
Experimental Setup
Experiments involve training Linear Recurrent Units (LRUs) across datasets of varying complexities, including MNIST and tasks from the Long Range Arena. Parameters are systematically adjusted, and reduction steps are strategically timed during warm-ups.
Results
Empirical evaluations demonstrate CompreSSM's efficacy in preserving expressive power while accelerating training. On datasets where model performance correlates with state dimensions, CompreSSM notably outperforms baseline models, delivering better results per unit of training time.
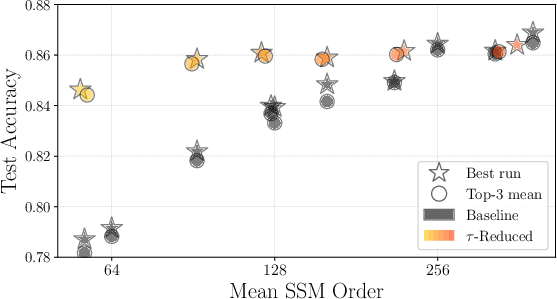
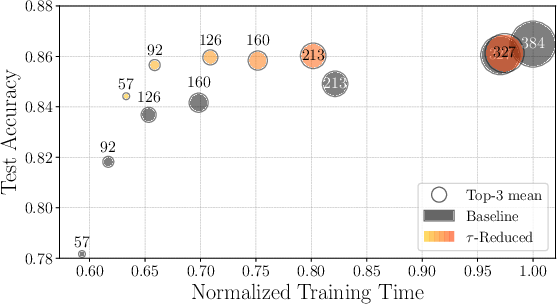
Figure 3: Test accuracy vs. Final state dimension.
Conclusion
CompreSSM introduces a novel in-training compression technique for SSMs leveraging balanced truncation. Empirical validation underscores its practicality and robustness, offering significant computational advantages in sequence modeling tasks. Future work could extend its application to selective models and linear time-varying systems, enhancing SSM's adaptability and efficiency in complex domains.



