2000 character limit reached
Reasoning Core: A Scalable RL Environment for LLM Symbolic Reasoning (2509.18083v1)
Published 22 Sep 2025 in cs.AI and cs.CL
Abstract: We introduce Reasoning Core, a new scalable environment for Reinforcement Learning with Verifiable Rewards (RLVR), designed to advance foundational symbolic reasoning in LLMs. Unlike existing benchmarks that focus on games or isolated puzzles, Reasoning Core procedurally generates problems across core formal domains, including PDDL planning, first-order logic, context-free grammar parsing, causal reasoning, and system equation solving. The environment is built on key design principles of high-generality problem distributions, verification via external tools, and continuous difficulty control, which together provide a virtually infinite supply of novel training instances. Initial zero-shot evaluations with frontier LLMs confirm the difficulty of Reasoning Core's tasks, positioning it as a promising resource to improve the reasoning capabilities of future models.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freeSummary
- The paper presents Reasoning Core, a scalable reinforcement learning environment that rigorously trains and evaluates LLMs on foundational symbolic reasoning tasks.
- It employs a continuous difficulty control and procedural generation to enable adaptive curricula and an endless supply of verified training instances.
- Empirical results with GPT-5 reveal challenges in deep symbolic manipulation, highlighting the benchmark's potential to drive advances in LLM reasoning.
Reasoning Core: A Scalable RL Environment for LLM Symbolic Reasoning
Motivation and Context
The paper presents Reasoning Core, a scalable RL environment designed to rigorously evaluate and train LLMs in foundational symbolic reasoning domains. The motivation stems from the limitations of existing benchmarks, which are either static and susceptible to contamination or procedurally generated but focused on narrow puzzles and games. Reasoning Core addresses these gaps by targeting high-generality domains such as PDDL planning, first-order logic, context-free grammar parsing, causal reasoning, and system equation solving. The environment is built to support Reinforcement Learning with Verifiable Rewards (RLVR), leveraging external verification tools to ensure solution correctness in complex symbolic tasks.
Design Principles and Architecture
Reasoning Core is characterized by several key design principles:
- High-Generality Task Selection: The environment focuses on domains that require robust, transferable reasoning strategies. Tasks include randomly generated PDDL planning domains, full first-order logic with equality, non-linear system equation solving, context-free grammar parsing, regex induction, symbolic induction, and causal reasoning via Bayesian networks. The inclusion of formal mathematics tasks (e.g., axiom/theorem matching, proof structure reconstruction) further broadens the scope.
- Procedural Generation and Difficulty Control: Each task is generated procedurally with a continuous "difficulty knob," allowing fine-grained adjustment of problem complexity. This enables adaptive curricula and ensures a virtually infinite supply of novel training instances, mitigating overfitting and supporting scalable RLVR training.
- External Verification: Solution correctness is assessed using specialized external tools (e.g., theorem provers, planning engines, symbolic algebra systems), moving beyond simple answer-checking to rigorous validation of structured outputs. This is essential for domains where internal verification is insufficient due to the complexity of the reasoning required.
- Efficient Data Production: The environment supports offline parallel generation and search-based pipelines, facilitating rapid production of diverse problems. Grammar-based generation is employed for tasks where concise, readable representations are beneficial, with custom algorithms controlling both minimum and maximum generation depth.
Task Suite and Problem Diversity
The suite of tasks in Reasoning Core is designed to probe a wide spectrum of symbolic reasoning capabilities:
- Planning: Models must generate valid action sequences in randomly constructed PDDL-like domains, with solutions validated for both syntactic and semantic correctness.
- Equation Systems: Tasks include solving linear systems, detecting underdetermined or inconsistent cases, and handling obfuscated equations.
- Regex Following and Induction: Models generate valid matches for complex regex patterns and induce regexes from positive/negative examples, with scoring based on classification accuracy and conciseness.
- Arithmetic and Sequential Induction: Tasks involve evaluating complex arithmetic expressions and inferring recursive formulas from numerical sequences.
- Formal Logic and Proof Tasks: These include conjecture entailment, theorem premise selection, proof reconstruction, and logic-based NLI, all leveraging automated theorem proving for validation.
- Set and Sequence Reasoning: Models perform set equality checks, intersection computation, missing element detection, and evidence retrieval in logical contexts.
- Parsing and Parsability: Tasks require generating parse trees for context-free grammars and determining string parsability/ambiguity.
- Causal Reasoning: Bayesian association and intervention tasks require exact inference and do-calculus-based reasoning in randomly generated networks.
Empirical Evaluation
Initial zero-shot evaluation of GPT-5 on Reasoning Core tasks demonstrates the challenging nature of the benchmark. Performance is assessed across two difficulty levels (easy and hard), with 200 samples per task and difficulty. The results indicate that all tasks are sufficiently challenging for GPT-5, and the difficulty control mechanism effectively increases failure rates at higher settings.
Figure 1: Zero-shot average reward of GPT-5 on Reasoning Core tasks, evaluated across two difficulty levels. Solid bar () is easy, dotted bar (hardSymbol) is hard. Each bar represents the average reward for a task, indicating GPT-5's ability to solve problems without prior training on Reasoning Core data. The results demonstrate the challenging nature of the benchmark, particularly at higher difficulty settings.
Notably, the benchmark exposes significant gaps in current LLM reasoning capabilities, especially in tasks requiring deep symbolic manipulation, formal logic inference, and causal reasoning. The continuous difficulty control allows for systematic analysis of model performance as a function of problem complexity.
Implementation and Practical Considerations
Reasoning Core is publicly available, with code and data accessible via GitHub, HuggingFace, and Prime Intellect. The environment is designed for integration with RLVR pipelines, supporting both offline and online training regimes. The use of external verification tools introduces computational overhead, particularly for theorem proving and planning tasks, but ensures rigorous reward signals. Efficient parallel generation and search-based instance selection mitigate data bottlenecks.
For practitioners, the environment enables:
- Curriculum learning via adaptive difficulty adjustment
- Robust evaluation of generalization to novel, unseen problems
- Training of LLMs on high-quality, verifiable reasoning data
- Fine-grained analysis of reasoning failures and bottlenecks
Resource requirements scale with the complexity of the external verification tools and the desired throughput of problem generation. The modular architecture allows selective inclusion of tasks and domains based on research objectives.
Theoretical and Practical Implications
The introduction of Reasoning Core has several implications:
- Benchmarking: It provides a rigorous, scalable benchmark for evaluating symbolic reasoning in LLMs, moving beyond static datasets and narrow procedural environments.
- RLVR Training: The environment supports the development of LLMs with improved reasoning capabilities via RLVR, leveraging verifiable rewards in expressive domains.
- Generalization and Robustness: By focusing on foundational tasks with high generality, Reasoning Core facilitates research into model generalization, transfer learning, and robustness to distributional shifts.
- Automated Curriculum Design: The continuous difficulty knob enables automated curriculum learning strategies, potentially accelerating model development and reducing manual intervention.
Future Directions
Potential future developments include:
- Expansion of task domains to cover additional areas of formal mathematics, scientific reasoning, and multi-modal symbolic tasks
- Integration with self-evolutionary curriculum generation systems, where models propose and verify their own training instances
- Optimization of external verification pipelines for increased scalability and reduced computational cost
- Systematic analysis of reasoning failures to inform architectural improvements in LLMs
Conclusion
Reasoning Core establishes a scalable, rigorous environment for RLVR-based training and evaluation of LLM symbolic reasoning. By targeting high-generality domains, leveraging external verification, and supporting adaptive difficulty control, it overcomes key limitations of existing benchmarks. The initial results with GPT-5 highlight the demanding nature of the tasks and the need for further advances in LLM reasoning. Reasoning Core is positioned as a critical resource for future research in robust, generalizable symbolic reasoning in AI.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces Reasoning Core, a giant “puzzle factory” for training and testing AI LLMs on solid, step-by-step thinking. Instead of relying on small, fixed sets of questions, it can endlessly create new, checkable problems in areas like logic, planning, grammar, equations, and cause-and-effect. The goal is to help future AIs learn deeper, more reliable reasoning skills.
What are the main questions?
The authors set out to answer three simple questions:
- How can we give AI models a never-ending stream of fresh, high-quality reasoning problems?
- How can we make sure each answer can be checked automatically (so models get fair, accurate feedback)?
- How can we smoothly adjust difficulty, like a slider in a video game, so models can learn from easy to hard?
How did they do it?
They built an environment called Reasoning Core that creates and checks problems in a few key ways:
Procedural generation (endless new puzzles)
Think of a level generator in a game: every time you play, it makes a new level. Here, the system creates new reasoning problems on the fly. This avoids the issue of models “memorizing” old questions and lets them practice on truly new ones.
Verifiable rewards (automatic referees)
When a model answers, the system uses outside tools—like a calculator for equations, a theorem prover for logic, or a planning engine for step-by-step plans—to check if the answer is correct. This is called Reinforcement Learning with Verifiable Rewards (RLVR): models try, get scored by an objective checker, and learn from that.
A difficulty knob (smooth, adjustable challenge)
Each problem type has a “difficulty slider” (a number) that makes tasks easier or harder (for example, more steps in a plan, more variables in equations, deeper proofs in logic). This helps build good learning “curricula” from simple to complex.
Efficient data production (lots of puzzles, fast)
They use parallel generation and search methods to produce many varied tasks quickly, so there’s always fresh training data.
What kinds of tasks?
Here are a few examples, explained simply:
- Planning (PDDL): Like figuring out a sequence of actions to reach a goal—similar to planning steps in a recipe or solving a maze.
- First-order logic: Working with “if… then…” rules about objects and their properties, not just simple true/false facts.
- Equations and systems: Solving sets of equations, and recognizing when there’s no solution or many solutions.
- Grammar parsing: Checking if a sentence fits certain rules and building its “parse tree” (the structure of a sentence).
- Regex (pattern matching): Finding or inventing strings that match a pattern (like spotting all emails or dates).
- Causal reasoning (Bayesian networks): Reasoning with probabilities and cause-and-effect, including the difference between observing something and forcing it (intervening).
- Induction tasks: Figuring out rules from examples, like guessing the formula behind a number sequence.
- Formal math proof tasks: Picking the right premises, checking if a theorem follows, and reconstructing proof steps using automated theorem provers.
- Set reasoning: Comparing lists to see if they have the same elements or finding their overlap.
What did they find?
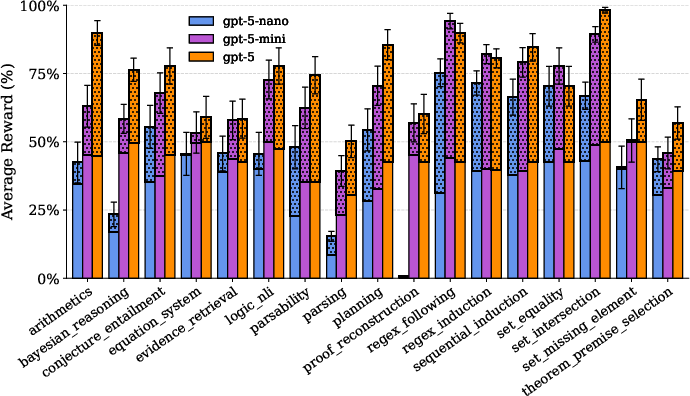
They tested a strong LLM (GPT‑5, zero-shot, meaning no special training on these tasks) on both easy and hard settings. The model struggled—especially on the hard versions. This shows:
- The tasks are genuinely challenging.
- The difficulty knob works: higher difficulty leads to more failures, as expected.
This is important because it suggests Reasoning Core can push models beyond simple tricks and test true, general reasoning skills.
Why does it matter?
- Better training for reasoning: Because every answer can be checked by reliable tools, models can learn by trial and error without needing human graders.
- Infinite, varied practice: The procedural generator provides diverse, fresh problems, reducing the risk that models just memorize datasets from the internet.
- Broad, foundational skills: By focusing on core symbolic areas (logic, planning, math, grammar, causality), models can learn reasoning strategies that transfer to many real situations.
- A community resource: The authors released code and data so researchers can build stronger, more trustworthy reasoning systems.
In short, Reasoning Core is like a well-designed gym for the “thinking muscles” of AI. It gives clear feedback, adjustable challenge, and a wide range of serious, meaningful exercises—setting the stage for future models to reason more reliably and generally.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored in the paper, formulated to guide future research.
- Absent RLVR training results: no experiments showing that training on Reasoning Core actually improves reasoning capability, sample efficiency, or generalization compared to baselines.
- Missing scaling curves: no analysis of performance as a function of training steps, dataset size, or difficulty level, preventing guidance on how to scale training effectively.
- No transfer evaluation: lack of evidence that gains on Reasoning Core translate to external benchmarks (e.g., GSM8K, MATH, SWE-Bench, ARC-AGI-2, Reasoning Gym).
- Single-model zero-shot evaluation: only GPT-5 with “low reasoning effort” is reported; broader model coverage, reasoning modes (CoT, tool-use), and reproducibility of the setup are absent.
- Reward function design: the RL interface, episode structure, reward shaping (e.g., partial credit, optimality bonuses), and negative rewards (for invalid outputs) are not specified.
- Cross-task reward comparability: no normalization or calibration of reward scales across tasks, complicating multi-task RL and curriculum scheduling.
- Difficulty knob validation: no quantitative evidence that difficulty is monotonic, stable, and comparable across tasks; only anecdotal “works as intended for most tasks.”
- Curriculum learning strategies: no experiments on adaptive curricula, difficulty scheduling policies, or automatic curriculum generation leveraging the “knob.”
- External solver robustness: unaddressed issues around solver timeouts, nondeterminism, parameterization, versioning, and potential verification errors affecting reward correctness.
- Computational cost of verification: lack of profiling of per-instance verification time, throughput, and cost—critical for large-scale RLVR training feasibility.
- Planning domain generator solvability: no analysis of how often randomly sampled PDDL-like domains are solvable, their plan-length distributions, or occurrence of degenerate/trivial cases.
- Plan optimality vs validity: it is unclear whether rewards incentivize optimal plans (length/cost) or accept any valid plan; the impact on learned policies is unexplored.
- Equation systems scope mismatch: paper claims “non-linear systems” in the overview, but the task section describes only linear systems—clarify scope and add non-linear coverage if intended.
- Regex engine semantics: the regex tasks use advanced constructs (e.g., possessive quantifiers
?+), but the exact engine and flags are unspecified; cross-engine differences and edge cases need reconciliation. - Handling multiple valid outputs: several tasks admit multiple correct solutions (plans, regexes, proofs); the acceptance criteria and tie-breaking (e.g., length penalties) are not systematically defined or validated.
- Parsing-task uniqueness guarantees: while instances are said to have a unique parse, the method to guarantee and verify uniqueness (especially under grammar ambiguities) is not described.
- Formal logic solver dependence: theorem/proof tasks rely on Vampire and superposition calculus; no ablation to test sensitivity to other provers or calculi, and no verification of proof minimality.
- Evidence retrieval correctness: beyond prover verification, evaluation of minimal evidence sets (necessity vs sufficiency) and tolerance for redundant but valid evidence is not discussed.
- Bayesian causal tasks coverage: the intervention tasks do not address identifiability challenges (back-door/front-door criteria), confounding, or causal discovery; only simple DAGs with known CPTs are considered.
- Probabilistic inference accuracy: there is no specification of acceptable error thresholds, numeric stability, or evaluation metrics (e.g., KL divergence) used for probabilistic tasks.
- Grammar-based generation bias: generators may introduce distributional artifacts (e.g., depth/shape biases); no statistical characterization of generated distributions or de-biasing strategies.
- Data diversity and domain coverage: tasks focus on text-only symbolic reasoning; multimodal reasoning (vision, code execution, program synthesis) and real-world knowledge integration are absent.
- Contamination assessment: no analysis of whether procedurally generated instances or TPTP-derived tasks overlap with models’ pretraining distributions (dataset contamination risks).
- Interoperability and APIs: the environment’s RL API, step-wise interaction model, and tool-usage affordances are unspecified, limiting adoption by RL practitioners.
- Partial credit and tolerance: how near-miss outputs (format deviations, equivalent but differently formatted parses/proofs) are scored is unclear; robust canonicalization and equivalence checking are unaddressed.
- Safety and reward hacking: no investigation into vulnerabilities where models exploit verifier quirks, formatting hacks, or solver bugs to obtain false positive rewards.
- Compute and throughput reporting: claims of “efficient data production” lack concrete throughput numbers, scaling bottlenecks, and resource requirements (CPU/GPU, RAM, solver parallelism).
- Reproducibility details: generator seeds, parameter ranges, solver versions, and evaluation scripts are not documented in the paper; reproducibility depends on external repositories without a formal protocol.
- Benchmark reliability: no psychometric analysis (difficulty discrimination, item response theory) to ensure tasks consistently measure the intended “foundational symbolic reasoning.”
- Task alignment with practical skills: limited discussion on how these tasks map to real-world applications (planning under constraints, formal verification tasks, causal reasoning in practice).
- Ablations on external verification: no experiments comparing internal vs external verification to quantify trade-offs in correctness, speed, and robustness.
- Comparative paper with Reasoning Gym: no head-to-head comparison on coverage, difficulty calibration, diversity, and downstream training effects to substantiate the “more foundational” claim.
- Multi-task training dynamics: absence of studies on interference, transfer, and balancing across tasks when trained jointly (e.g., task weighting, sampling policies).
- Long-context reasoning: while related work references long-context logic, the environment does not specify tasks stressing context length, memory, or attention robustness.
- Encoding robustness: examples show encoding artifacts (e.g., “Ã9.”); no assessment of robustness to Unicode/encoding variations in inputs and outputs.
- Licensing and maintenance: dataset licensing, long-term maintenance of external tool dependencies, and versioning/compatibility guarantees are not stated.
- Evaluation metrics standardization: beyond average reward, task-specific metrics (proof minimality, plan optimality, regex conciseness, parse correctness) are not standardized or reported.
- Human baselines: no human baselines or expert benchmarks to contextualize difficulty and validate that tasks assess reasoning rather than esoteric solver-specific idiosyncrasies.
- Auto-curriculum/self-play integration: despite references to self-evolutionary curricula, the paper does not integrate or evaluate auto-curriculum methods within Reasoning Core.
- Robust formatting specifications: strict output formats are required (e.g., Lisp-style parse trees), but the paper lacks canonicalization guidelines and validators to reduce formatting-induced failures.
- Generalization across generator shifts: no tests of robustness to generator hyperparameter shifts or out-of-distribution instances within the same domain (e.g., deeper grammars, larger DAGs).
- Tool-use training: unclear whether environments support and encourage tool-use behaviors (calling planners/provers) and how such behaviors are evaluated or rewarded.
Practical Applications
Immediate Applications
Below is a set of actionable use cases that can be deployed now, based on the paper’s environment, generators, and verifiable tooling.
- RLVR training data source for reasoning-focused LLM post-training (AI research, model providers)
- Use Reasoning Core’s procedurally generated, verifiable tasks to fine-tune LLMs on symbolic reasoning (planning, logic, equations, grammar, regex).
- Tools/workflows: Integrate the GitHub library and HF dataset into RL pipelines (e.g., PPO/GRPO with external verifiers like Vampire, planning engines, CAS).
- Assumptions/dependencies: Access to external solvers; GPU/TPU compute; prompt/execution sandboxing for verification; stable interfaces to Prime Intellect environment.
- Robust reasoning benchmarking and continuous evaluation (academia, AI labs, model vendors)
- Establish internal leaderboards using continuous difficulty knobs to track progress across foundational domains.
- Tools/workflows: CI-style eval harness; contamination-resistant eval streams; adaptive difficulty sweeps.
- Assumptions/dependencies: Agreement on task settings; careful reporting to avoid “leaderboard illusion.”
- Grammar/regex assistants for developer tooling (software)
- Use regex_following/regex_induction and CFG parsing/parsability to auto-generate tests, fix patterns, and verify parsers.
- Tools/products: IDE plugins that propose and validate regexes; parser test generators; CI checks for grammar ambiguity.
- Assumptions/dependencies: Mapping between synthetic patterns and project-specific DSLs; integration with existing build/test systems.
- Planning micro-benchmarks for agent workflows (robotics, operations, RPA)
- Train and evaluate planning modules using random PDDL domains to improve action sequencing in task automation.
- Tools/workflows: Agent pipelines with planner-calls, plan verification, and curriculum progression via “difficulty knob.”
- Assumptions/dependencies: Domain transfer from synthetic PDDL to real task schemas; action grounding in actuators/APIs.
- Logic-aware retrieval and evidence selection (knowledge management, RAG systems)
- Use logic_nli and evidence_retrieval to train retrievers that select minimal supporting statements for entailment/contradiction.
- Tools/workflows: RAG with formal verification layers that score candidate evidence sets.
- Assumptions/dependencies: Formalization of domain knowledge into predicates; compatibility with theorem prover interfaces.
- Causal analytics helpers for A/B testing and observational studies (marketing, healthcare analytics, policy analysis)
- Use bayesian_association/intervention tasks to train LLMs that distinguish observational vs interventional queries and compute posteriors.
- Tools/products: “do-calculus assistants” for experiment design; dashboards that surface causal dependencies.
- Assumptions/dependencies: Accurate mapping from real data to Bayesian networks; careful calibration against domain priors.
- ETL/data pipeline checks with symbolic tasks (data engineering)
- Employ set_equality/intersection tasks to validate data merges, deduplication, and schema reconciliations.
- Tools/workflows: Lightweight verifiable checks embedded in ETL DAGs; failing cases escalate to human review.
- Assumptions/dependencies: Reliable transformation of real objects into canonical comparable representations.
- Auto-graders and adaptive drills for foundational reasoning (education)
- Generate graded exercises in arithmetic, sequences, formal logic, and parsing with verifiable feedback and adaptive difficulty.
- Tools/products: LMS plugins that consume Reasoning Core generators; instructor dashboards for skill diagnostics.
- Assumptions/dependencies: Alignment of task taxonomy with curricula; student privacy and assessment policies.
- Auditable proof and dependency tracing (compliance, internal validation)
- Use proof_reconstruction/theorem_premise_selection to require structured derivations and minimal premise sets for internal decisions.
- Tools/workflows: “Reasoning ledger” that stores verifiable steps for audits and post-mortems.
- Assumptions/dependencies: Domain-specific formalization; staff training to interpret proof graphs.
- Synthetic dataset production to alleviate data scarcity (academia, open-source communities)
- Scale generation of diverse, verifiable reasoning corpora for public benchmarks and training (e.g., SYNTHETIC-1 style).
- Tools/workflows: Distributed data generation pipelines with offline parallelization; quality filters via external solvers.
- Assumptions/dependencies: Compute budget; governance for open release; consistent metadata and versioning.
Long-Term Applications
These applications require further research, scaling, domain integration, or regulatory maturity before widespread deployment.
- General-purpose verified reasoning models for complex multi-domain tasks (cross-sector)
- Train LLMs that can plan, prove, parse, and compute in one agent, backed by verifiable reward signals.
- Tools/products: “Verified Reasoning Core” foundation models; orchestration to call external solvers seamlessly.
- Assumptions/dependencies: Large-scale RLVR compute; robust tool-use and error handling; persistent solver availability.
- Safety-critical decision systems with formal verification layers (healthcare, autonomous systems, industrial control)
- Use external theorem provers/planners to validate outputs from agentic LLMs before actuation or recommendation.
- Tools/workflows: Guardrails that enforce logical consistency and plan feasibility; safety cases built from proof artifacts.
- Assumptions/dependencies: High accuracy, domain-grounded models; certification; integration with clinical/vehicle systems.
- Enterprise process orchestration via symbolic planning (finance ops, logistics, energy operations)
- Model workflows in PDDL-like schemas and let agents compute valid plans, with verifiable correctness and optimality targets.
- Tools/products: “LLM Planner Orchestrator” tied to BPM suites; simulators and real-time plan validators.
- Assumptions/dependencies: Mapping enterprise processes to formal domains; change management; latency requirements.
- Math research co-pilots and formalization bridges (academia)
- Combine TPTP tasks with natural language guidance to help formalize conjectures, find axioms, and reconstruct proofs.
- Tools/products: Interactive theorem-proving assistants that suggest axiom subsets and dependency graphs.
- Assumptions/dependencies: Strong NL↔formal translation; collaboration with theorem-proving communities; proof checking at scale.
- Explainability-by-construction through proof artifacts (regulatory compliance, audits)
- Require models to output structured derivations; store and review minimal evidence sets for critical decisions.
- Tools/workflows: Proof UIs and explainer pipelines; differential proof comparison for policy changes.
- Assumptions/dependencies: Usability of proof representations; standards for interpretability; legal acceptance.
- Personalized, mastery-based reasoning education (education)
- End-to-end adaptive tutors spanning logic, algebra, grammar parsing, and causal reasoning with calibrated curricula.
- Tools/products: “Core Reasoning Tutor” with live difficulty control and verifiable grading; teacher co-pilots.
- Assumptions/dependencies: Longitudinal learning models; alignment and fairness; content accreditation.
- Policy labs for simulated interventions and causal scenario planning (government, NGOs)
- Use Bayesian network generators to encode policy variables and test intervention outcomes under uncertainty.
- Tools/products: Simulation platforms for policy “do-operator” experiments; sensitivity analyses.
- Assumptions/dependencies: Faithful causal models; robust data; stakeholder buy-in.
- Scientific discovery assistants via symbolic induction (materials, biotech, energy)
- Infer candidate formulas from sequences/data and validate with external algebra systems and experiments.
- Tools/workflows: Hypothesis generators that produce verifiable symbolic relations; lab-in-the-loop validation.
- Assumptions/dependencies: High-precision numeric pipelines; experimental integration; domain knowledge constraints.
- Verified financial modeling and compliance engines (finance)
- Encode constraints and proofs for risk, pricing, and regulatory checks; use premise selection to ensure minimal, sufficient bases.
- Tools/products: “Formal Compliance Co-pilot” that produces auditable derivations and detects contradictions.
- Assumptions/dependencies: Domain formalization; regulator collaboration; performance on large, real datasets.
- Software verification and synthesis with solver-backed LLMs (software, cybersecurity)
- Combine CFG/regex tasks and logic verification to synthesize parsers, validate protocols, and detect ambiguous grammars.
- Tools/products: Co-pilots that propose specs and prove properties; CI gates for formal checks.
- Assumptions/dependencies: Scaling to real codebases; integration with formal methods toolchains; developer adoption.
- Standardized, open reasoning benchmarks shaping industry norms (AI ecosystem)
- Establish community-maintained, procedurally generated, contamination-resistant benchmarks with verifiable rewards.
- Tools/workflows: Benchmark hubs with difficulty schedules, metadata, and solver-integrated scoring.
- Assumptions/dependencies: Broad participation; governance; reproducibility infrastructure.
- Tool ecosystems and marketplaces around verifiable reasoning (platforms)
- Offer hosted environments (e.g., Prime Intellect) for training/evaluation, solver-as-a-service, and dataset generation APIs.
- Tools/products: Managed RLVR services; problem generators with SLAs; audit trails.
- Assumptions/dependencies: Cost-effective hosting; reliability; licensing for external solver components.
Glossary
- Bayesian inference: A method for updating probabilities based on evidence within a probabilistic model. "Models must perform exact Bayesian inference"
- Bayesian networks: Probabilistic graphical models representing variables and their conditional dependencies via a directed acyclic graph. "randomly sampled bayesian networks."
- Conditional independence: A property where two variables are independent given the value of a third variable. "conditional independence relationships"
- Conditional probability distribution: The distribution of a variable conditioned on the values of its parent variables. "conditional probability distributions dependent on its parents"
- Conjunctive Normal Form (CNF): A standardized logical form as a conjunction of disjunctions, commonly used in automated theorem proving. "cnf(distribute1,axiom,(multiply(X1,add(X2,X3))=add(multiply(X1,X2),multiply(X1,X3))))"
- Context-free grammar (CFG): A formal grammar where production rules replace a single nonterminal, used to define languages and parse strings. "a context-free grammar"
- Derivation graph: A graph showing how theorems or clauses are derived from axioms via inference steps. "constructs derivation graphs"
- Directed acyclic graph (DAG): A directed graph with no cycles, often used to represent causal or dependency structures. "random directed acyclic graphs"
- Do-calculus: A set of rules for reasoning about interventions and causal effects in graphical models. "applies do-calculus"
- do-operator: Notation from causal inference representing intervention on a variable to set its value. "using the do-operator"
- Dyck languages: A family of context-free languages consisting of properly balanced and nested brackets, used to model nested structures. "Dyck languages"
- First-order logic with equality: First-order logic extended with an equality predicate that satisfies reflexivity, symmetry, and transitivity. "First-order logic with equality"
- Fluent arity: In planning, the number of arguments that a state predicate (fluent) takes. "fluent arities"
- Full-match semantics: Regex matching mode where the entire string must match the pattern, not just a substring. "full-match semantics"
- Interventional distribution: The probability distribution of variables after an external intervention is applied in a causal model. "interventional distributions"
- Meta-grammar: A grammar that generates grammars, enabling structured generation of diverse CFGs. "using a meta-grammar that produces grammars"
- Parametric difficulty: A difficulty setting controlled by parameters to systematically vary task complexity. "parametric difficulty"
- Paramodulation: An inference rule in equational theorem proving for reasoning with equality. "Resolution and Paramodulation"
- PDDL (Planning Domain Definition Language): A standardized language for specifying planning problems and domains. "PDDL planning"
- Posterior probability distribution: The updated probability distribution of a variable after observing evidence. "posterior probability distributions"
- Premise selection: Choosing a minimal set of premises sufficient to prove a theorem. "minimal subset of premises"
- Procedural content generation (PCG): Algorithmic generation of data or environments to provide scalable, diverse tasks. "procedural content generation (PCG)"
- Proof dependency graph: A graph that encodes which clauses or statements derive from which others in a proof. "proof dependency graphs"
- Proof depth: The length or maximal number of inference steps in a proof. "proof depth in logic"
- Reinforcement Learning with Verifiable Rewards (RLVR): Training paradigm where environments algorithmically verify solution correctness to provide reward signals. "Reinforcement Learning with Verifiable Rewards (RLVR)"
- Resolution: A fundamental inference rule in propositional and first-order logic used to derive contradictions or new clauses. "Resolution and Paramodulation"
- Stochastic rounding: A rounding technique that randomly rounds values up or down based on their fractional part to preserve expectations. "stochastic rounding"
- Superposition Calculus: A refutationally complete inference system for first-order logic with equality. "Superposition Calculus"
- Theorem prover: An automated system that attempts to prove or refute logical statements from a set of axioms. "theorem provers"
- TPTP ecosystem: A collection of standard problem libraries, formats, and tools for automated theorem proving. "the TPTP ecosystem"
- Underconstrained system: A system of equations with fewer independent equations than variables, yielding multiple solutions. "underconstrained systems"
- Vampire prover: A state-of-the-art automated theorem prover based on the superposition calculus. "Vampire prover"
- Well-posed problem: A problem that has a solution that exists, is unique, and depends continuously on inputs. "well-posed problems"
- Zero-shot: Evaluation or learning without task-specific training examples. "zero-shot evaluation"
Collections
Sign up for free to add this paper to one or more collections.