TDRM: Smooth Reward Models with Temporal Difference for LLM RL and Inference (2509.15110v1)

Abstract: Reward models are central to both reinforcement learning (RL) with LLMs and inference-time verification. However, existing reward models often lack temporal consistency, leading to ineffective policy updates and unstable RL training. We introduce TDRM, a method for learning smoother and more reliable reward models by minimizing temporal differences during training. This temporal-difference (TD) regularization produces smooth rewards and improves alignment with long-term objectives. Incorporating TDRM into the actor-critic style online RL loop yields consistent empirical gains. It is worth noting that TDRM is a supplement to verifiable reward methods, and both can be used in series. Experiments show that TD-trained process reward models (PRMs) improve performance across Best-of-N (up to 6.6%) and tree-search (up to 23.7%) settings. When combined with Reinforcement Learning with Verifiable Rewards (RLVR), TD-trained PRMs lead to more data-efficient RL -- achieving comparable performance with just 2.5k data to what baseline methods require 50.1k data to attain -- and yield higher-quality LLM policies on 8 model variants (5 series), e.g., Qwen2.5-(0.5B, 1,5B), GLM4-9B-0414, GLM-Z1-9B-0414, Qwen2.5-Math-(1.5B, 7B), and DeepSeek-R1-Distill-Qwen-(1.5B, 7B). We release all code at https://github.com/THUDM/TDRM.

• The paper introduces temporal difference learning using n-step updates to combine immediate and future rewards for smoother feedback in LLM reinforcement learning.
• Experiments show up to a 23.7% improvement in inference performance and comparable results with only 2.5k training samples versus over 50k in baseline models.
• The integration of process-based and rule-based rewards enhances reward signal stability, leading to improved efficiency and decision-making in RL.

TDRM: Smooth Reward Models with Temporal Difference for LLM RL and Inference

Introduction

The paper "TDRM: Smooth Reward Models with Temporal Difference for LLM RL and Inference" introduces a novel method for improving reward models in reinforcement learning (RL) with LLMs. The key innovation is the use of temporal difference (TD) learning to achieve smoother, more reliable reward signals, addressing the lack of temporal consistency in existing reward models that leads to sparse guidance and instability during training.

Reward Models (RMs) are integral to RL systems, providing feedback not just at the end of the reasoning process but throughout it. Current models, including Process Reward Models (PRMs) and Outcome Reward Models (ORMs), offer distinct advantages but struggle with continuity over long reasoning chains, often degrading training signals and inference efficiency.

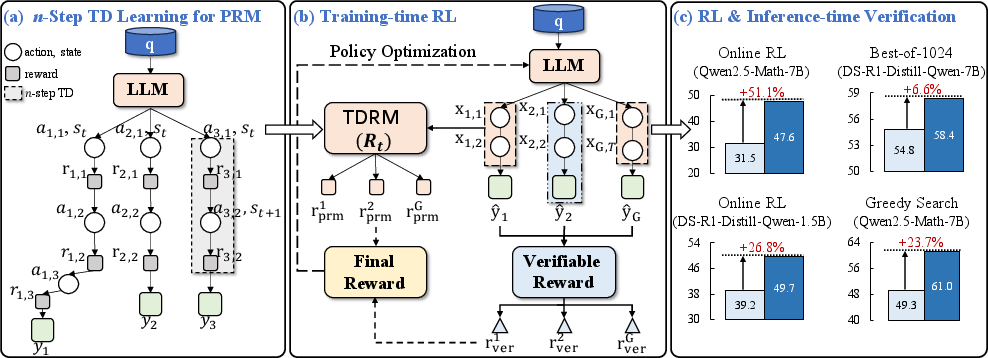
Figure 1: Overall framework of TDRM with temporal difference learning to enhance reward model smoothness.

Methodology

Temporal Difference Learning

TDRM leverages temporal difference learning to address the shortcomings of existing reward models. By introducing $n$-step TD updates, the paper combines immediate reward signals with estimates of future value, ensuring that intermediate reasoning steps are rewarded dynamically, improving the alignment with long-term objectives.

This approach refines the state value estimates, where the reward function dynamically updates based on a combination of immediate and future rewards. The $n$-step TD algorithm computes cumulative rewards over $n$ subsequent states and uses these to bootstrap intermediate state values.

Reward Modeling and Smoothness

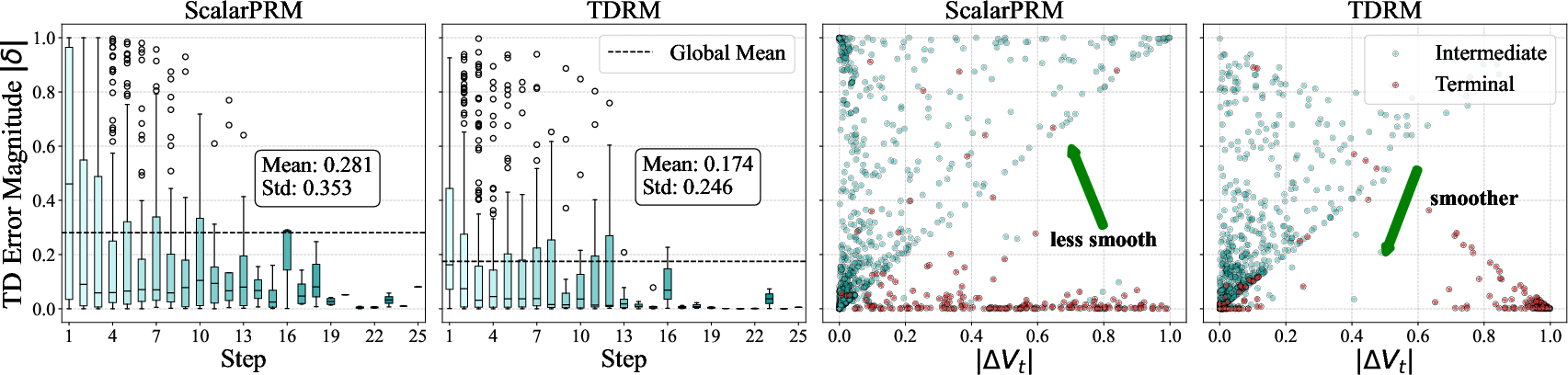
Reward smoothness is crucial for effective LLM reasoning. By minimizing TD error and controlling reward volatility, the TDRM method achieves temporally consistent feedback, critical for both intermediate and final reasoning steps.

• Smoothness Metrics: The paper introduces metrics like TD error magnitude and value difference to quantify smoothness. These metrics show that TDRM provides more stable state value updates than ScalarPRM, a traditional approach to reward modeling.

  Figure 2: Comparison of reward model smoothness showing reduced TD error with TDRM.

Integration with RL

The integration of TDRM within RL is achieved through a linear combination of the process-based rewards from the PRM and rule-based verifiable rewards. This balance enhances feedback density and improves training efficiency, critical to achieving superior performance with minimal data.

Experiments

Settings and Benchmarks

TDRM's performance was evaluated in two key scenarios: inference-time verification (using Best-of-$N$ sampling and greedy search) and training-time reinforcement learning. Experiments highlight TDRM's advantage in smooth reward distribution and enhanced RL outcomes.

Results

The experimental results demonstrate TDRM's edge in achieving higher accuracy and smoother transitions in reward landscapes compared to conventional models:

• Inference-Time Verification: Best-of-$N$ sampling results showed up to a 6.6% gain for $N=128$ and 23.7% for tree-search strategies when employing TDRM over baseline PRMs.
• Training-Time RL Performance: In RL applications, TDRM-trained models consistently outperform leading RL frameworks in accuracy and data efficiency, achieving comparable success with only 2.5k data samples where others require over 50k.

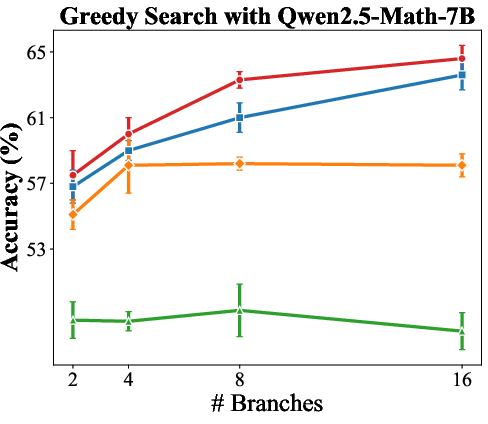
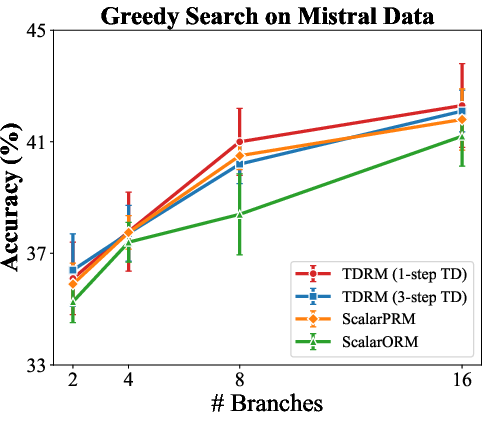
Figure 3: Results of greedy search highlighting enhanced PRM performance with TDRM.

Conclusion

TDRM establishes itself as a reliable technique for reinforcing temporal consistency in reward modeling, particularly within RL and inference applications involving LLMs. By stabilizing reward signals and enhancing feedback density, TDRM addresses a critical bottleneck in current systems, paving the way for improved RL efficiency and reasoning quality in AI models.

Future work can explore more diverse applications for TDRM outside mathematical reasoning, potentially extending its impact across AI research domains simulating complex decision-making processes. The release of code alongside this research aims to promote further exploration and innovation in this area.