Emergent Alignment via Competition (2509.15090v1)
Abstract: Aligning AI systems with human values remains a fundamental challenge, but does our inability to create perfectly aligned models preclude obtaining the benefits of alignment? We study a strategic setting where a human user interacts with multiple differently misaligned AI agents, none of which are individually well-aligned. Our key insight is that when the users utility lies approximately within the convex hull of the agents utilities, a condition that becomes easier to satisfy as model diversity increases, strategic competition can yield outcomes comparable to interacting with a perfectly aligned model. We model this as a multi-leader Stackelberg game, extending Bayesian persuasion to multi-round conversations between differently informed parties, and prove three results: (1) when perfect alignment would allow the user to learn her Bayes-optimal action, she can also do so in all equilibria under the convex hull condition (2) under weaker assumptions requiring only approximate utility learning, a non-strategic user employing quantal response achieves near-optimal utility in all equilibria and (3) when the user selects the best single AI after an evaluation period, equilibrium guarantees remain near-optimal without further distributional assumptions. We complement the theory with two sets of experiments.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper asks a big question: Can we get the benefits of “aligned” AI (AI that cares about what humans want) even if no single AI is perfectly aligned? The authors show that if you can talk to several different AIs that each have their own goals, then their competition to influence you can lead to outcomes that are almost as good as having one perfectly aligned AI—under a simple, realistic condition about how your preferences relate to theirs.
What are the key questions?
The paper focuses on three easy-to-understand questions:
- If a perfectly aligned AI could help a user pick the best choice, can multiple misaligned AIs, by competing, still help the user get the best outcome?
- If the user isn’t perfectly strategic and makes choices “softly” (leaning toward better options without always picking the absolute best), can competition still guarantee near-best results?
- If the user tries all the AIs for a while and then picks the single best one to use going forward, does competition still make the user’s results near-optimal without needing extra assumptions?
How did they paper it? (Methods and ideas in everyday language)
Think of the user (Alice) as someone making a decision—like choosing a movie to watch, a medicine to prescribe, or a policy to support. The “best” choice depends on facts about the world that she doesn’t fully know. She can talk to several AIs (the paper calls them Bob 1, Bob 2, …, Bob k), and each AI has its own goals (for example, an AI might subtly prefer one company’s drug or one kind of movie).
Here are the main ideas in simpler terms:
- Utility: This is a score for how much Alice likes the outcome (higher is better). Each AI also has its own scoring system.
- “Convex hull” condition: Imagine you can “blend” the AIs’ preferences in different proportions. If, by mixing them, you can closely match Alice’s preferences, then the condition holds. In plain words: Alice’s taste is somewhere near a smart combination of the AIs’ tastes.
- Competition: Each AI commits to a way of talking (its “strategy” for the conversation) before Alice interacts with them. After seeing their strategies, Alice chooses how to talk to them and, at the end, picks an action.
- Equilibrium: A steady situation where no AI can switch its strategy and get a better result for itself, given what the others are doing and how Alice responds.
- Bayes-optimal action: The best choice Alice could make if she knew everything relevant (or could learn enough from the conversation).
- Quantal response: Instead of always picking the absolute top-scoring action, Alice chooses actions with probabilities that favor higher-scoring options. It’s like leaning toward better choices, but allowing some chance of picking near-best ones—more realistic for human decision-making.
They build a game-theory model (a “multi-leader Stackelberg game”) where:
- The AIs act as “leaders” who fix their conversation strategies first.
- Alice acts as the “follower,” sees those strategies, talks to them, and then makes her choice.
- The competition among AIs shapes how much useful information Alice gets and how good her final decision is.
What did they find, and why does it matter?
The authors prove three main results:
1) When perfect alignment would let Alice learn the truly best action, competition among misaligned AIs can still get her to the same best outcome—if her preferences can be approximated by mixing the AIs’ preferences.
- Why this matters: Even if no single AI is perfectly aligned, diverse AIs competing to influence Alice can “push” the conversation toward revealing the information she needs to make the best decision.
2) If Alice uses a simple, realistic decision rule (quantal response) and reports her beliefs honestly while talking to the AIs, she still gets near-best outcomes in all equilibria—even under weaker assumptions.
- Why this matters: People aren’t perfectly rational robots. This shows the guarantees don’t break if the user makes choices in a “soft,” human-like way.
3) If Alice tests all the AIs first and then picks the single best one to use going forward, she still gets near-best results at equilibrium without needing extra assumptions about the world.
- Why this matters: This mirrors real life—users try several tools and settle on one. It suggests that a competitive AI market can deliver good outcomes even if alignment isn’t perfect.
They also provide two kinds of evidence:
- Synthetic utility functions: They simulate AIs by slightly changing the prompts of a LLM and evaluate them on:
- Movie recommendations (MovieLens data)
- Ethical judgment questions (ETHICS data)
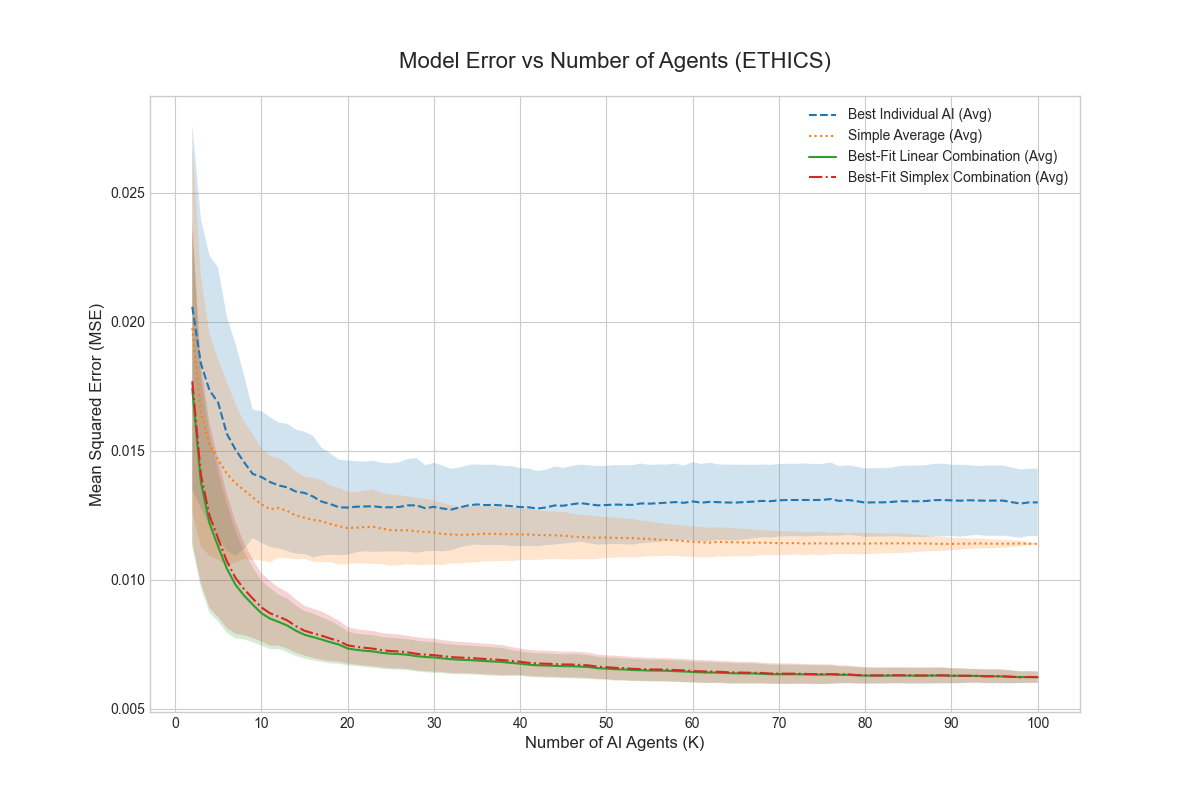
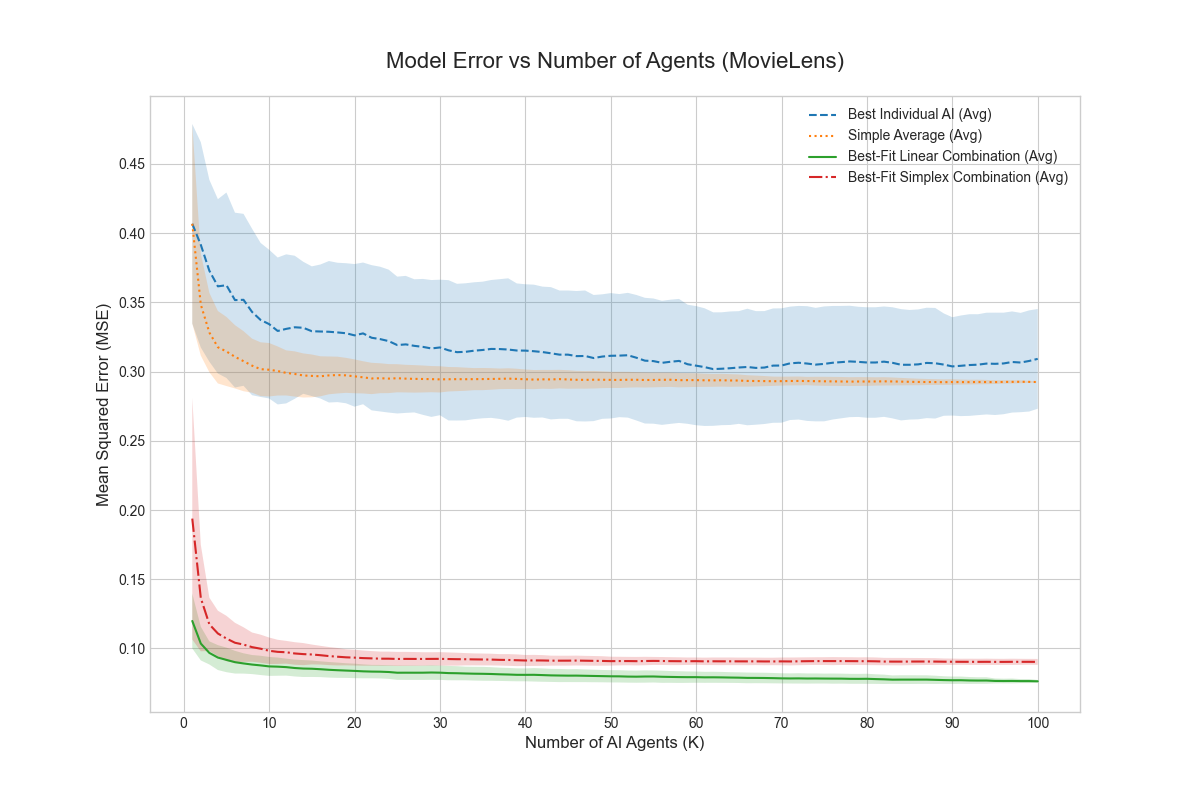
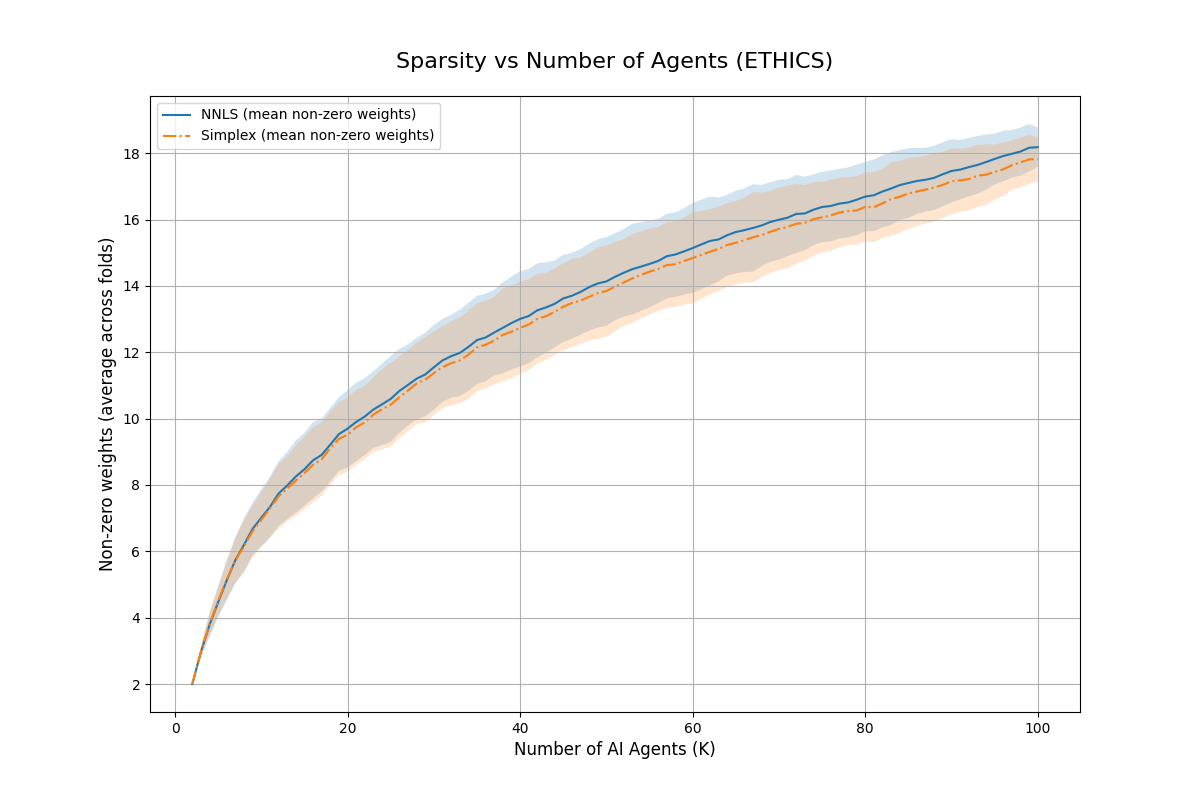
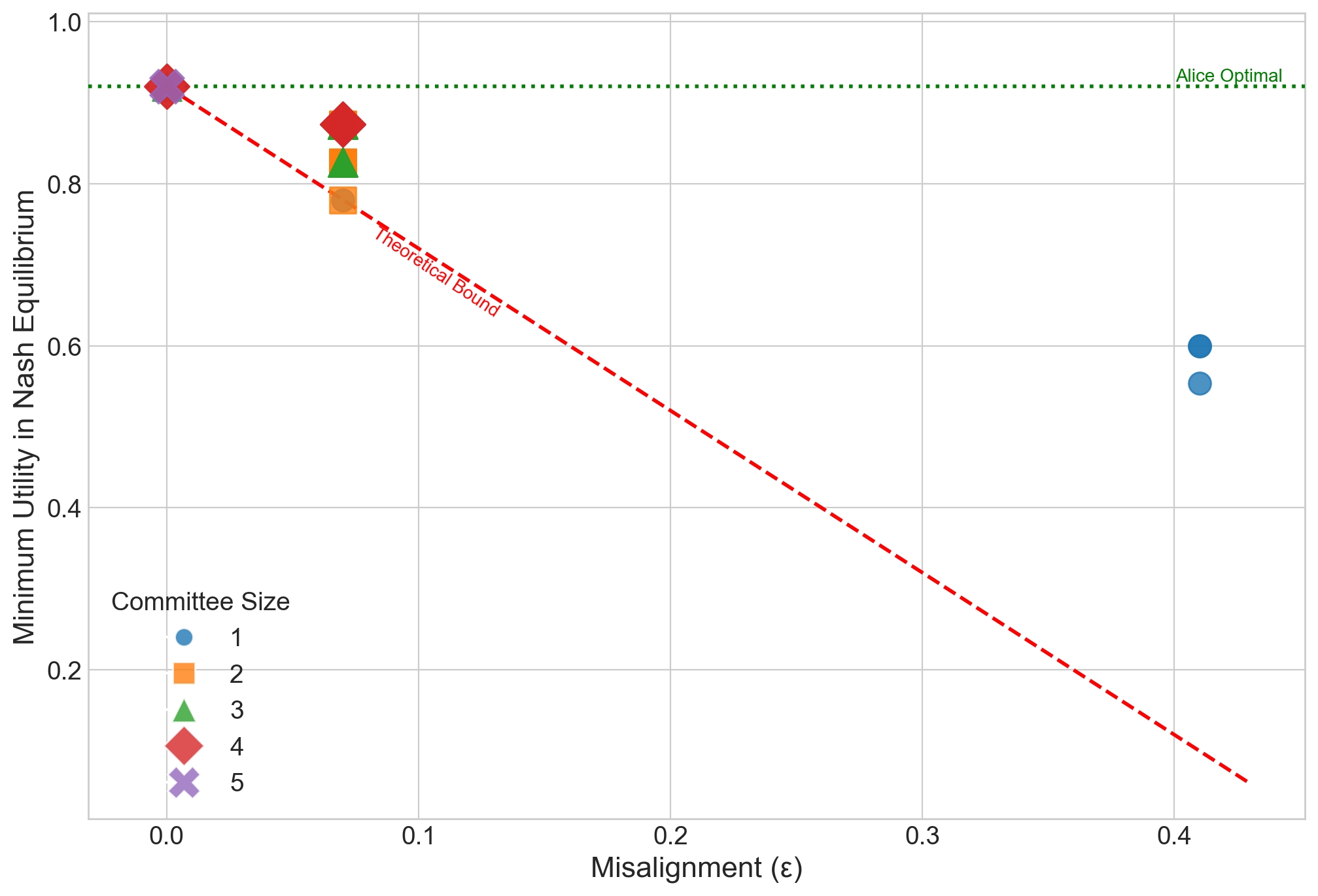
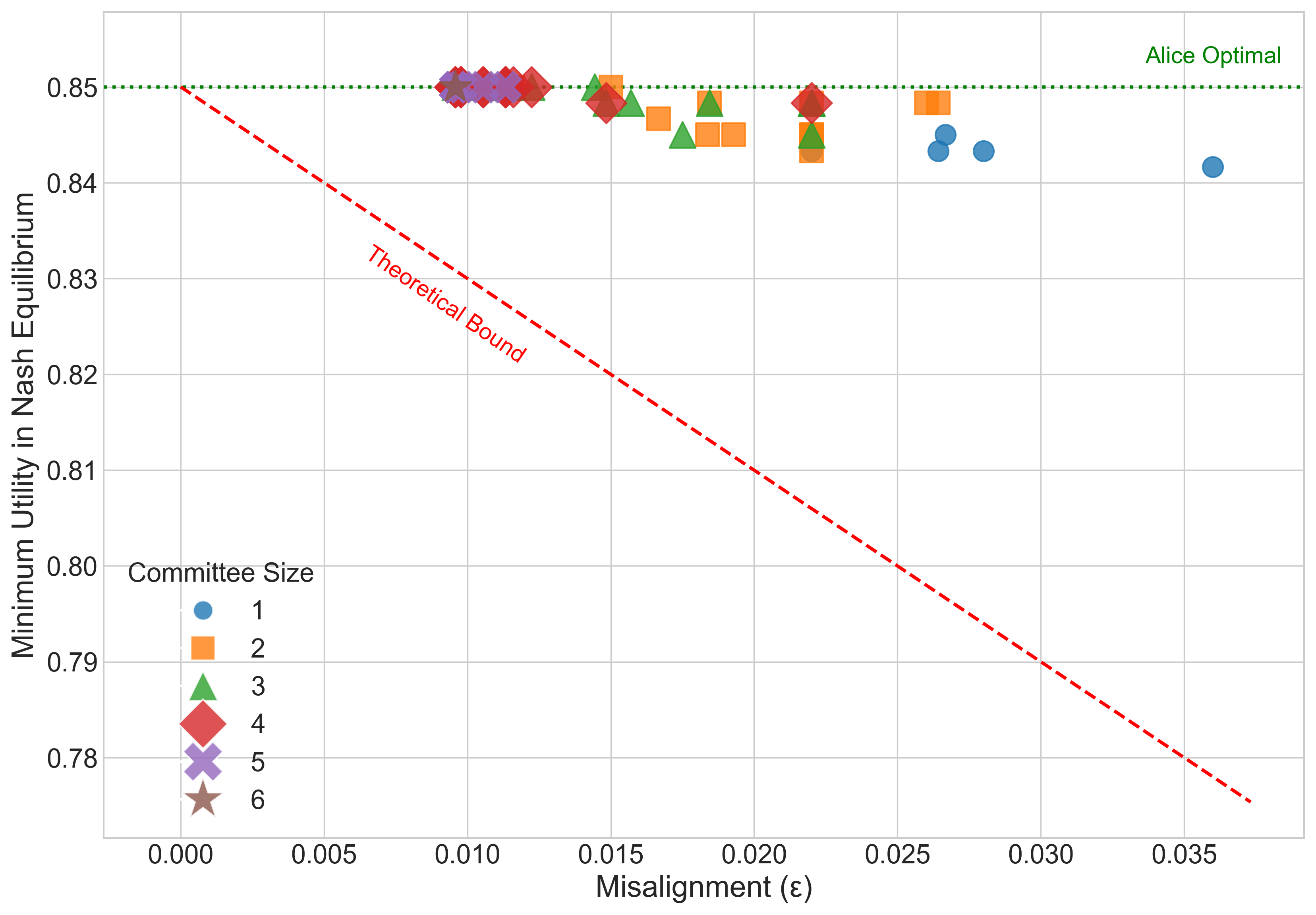
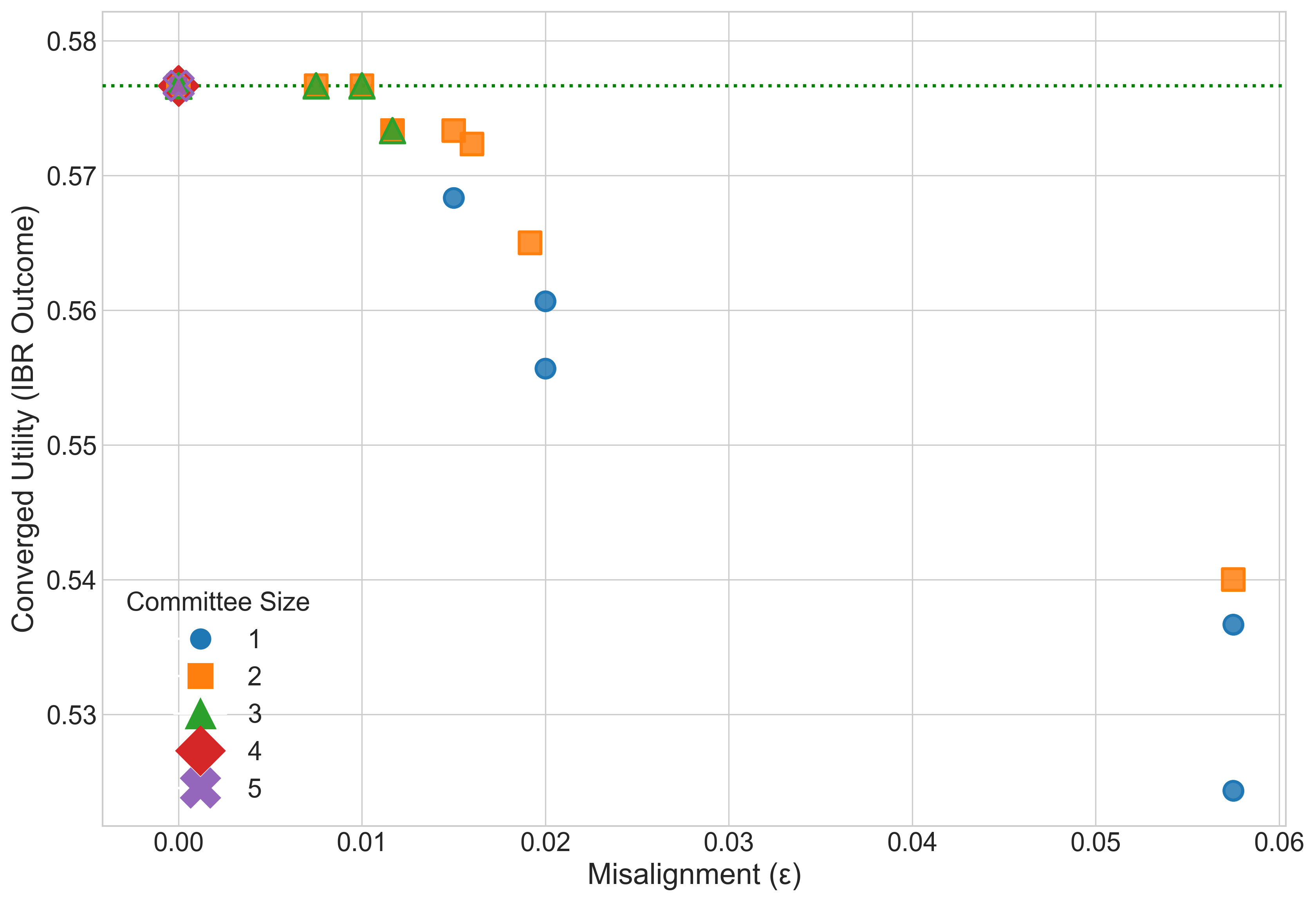
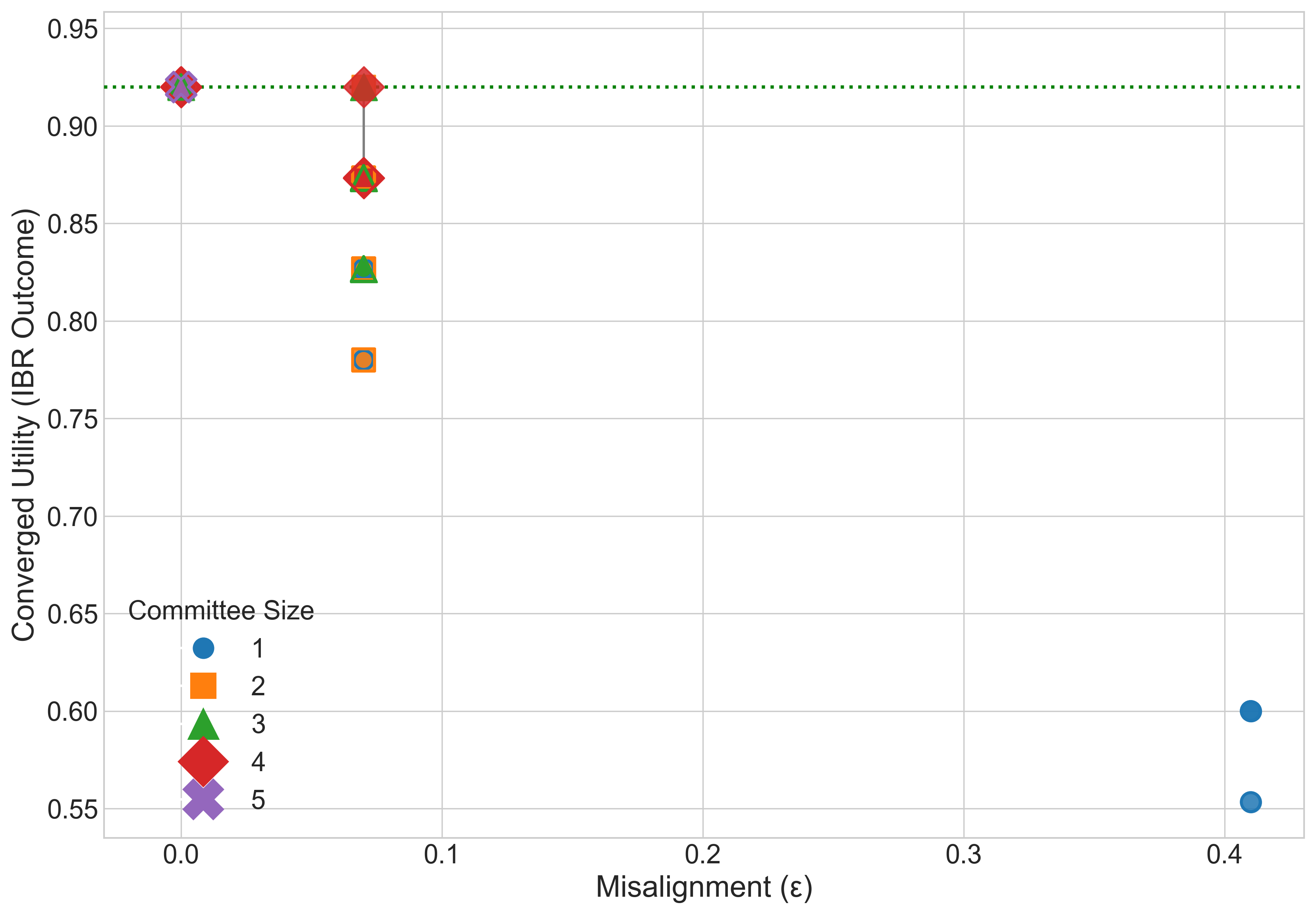
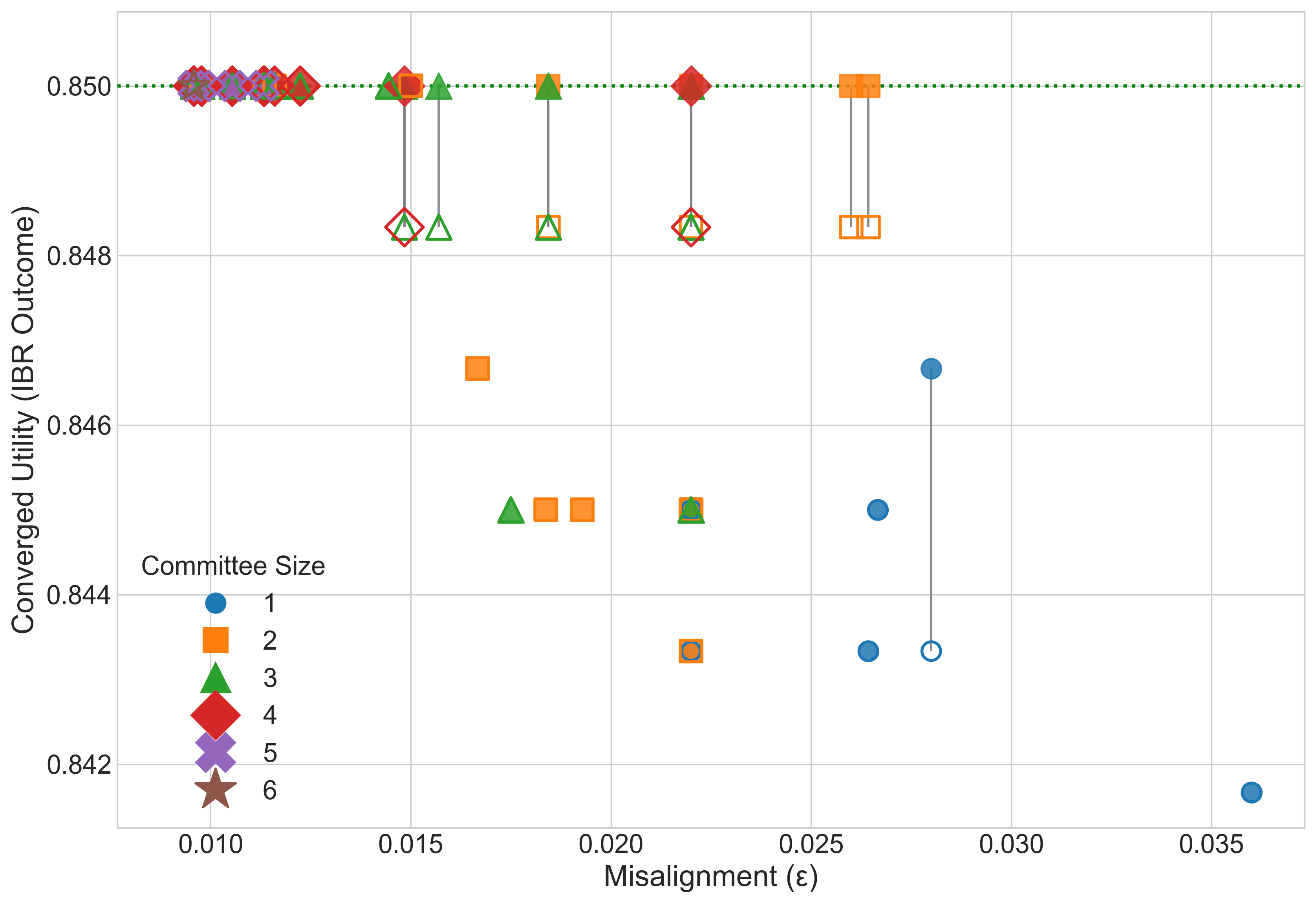
Result: Even when each single AI is not well aligned, the “best mix” of them (their convex hull) closely matches a target “human” utility. This supports the core idea that a smart blend of different AIs can be much more aligned than any one AI alone.
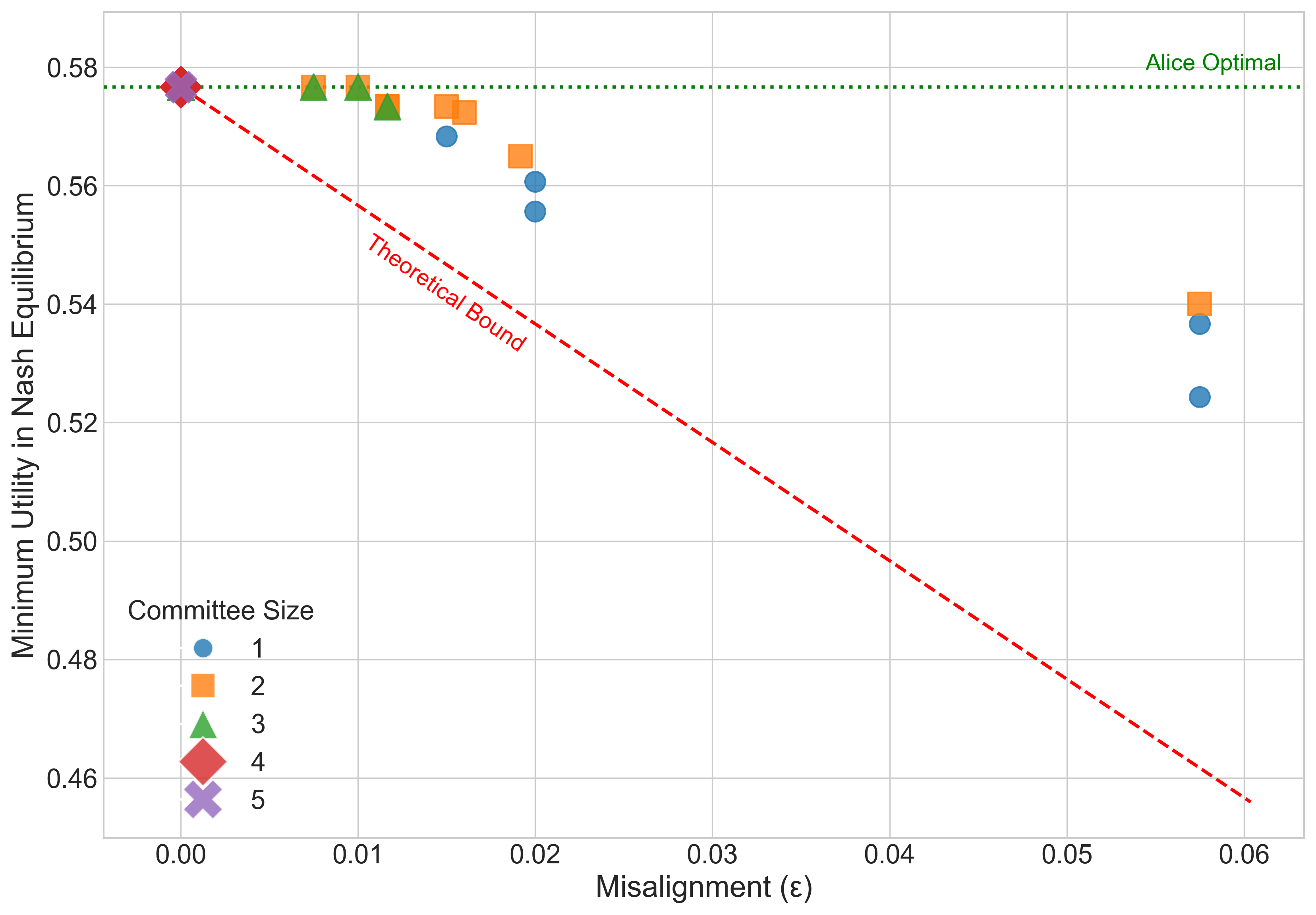
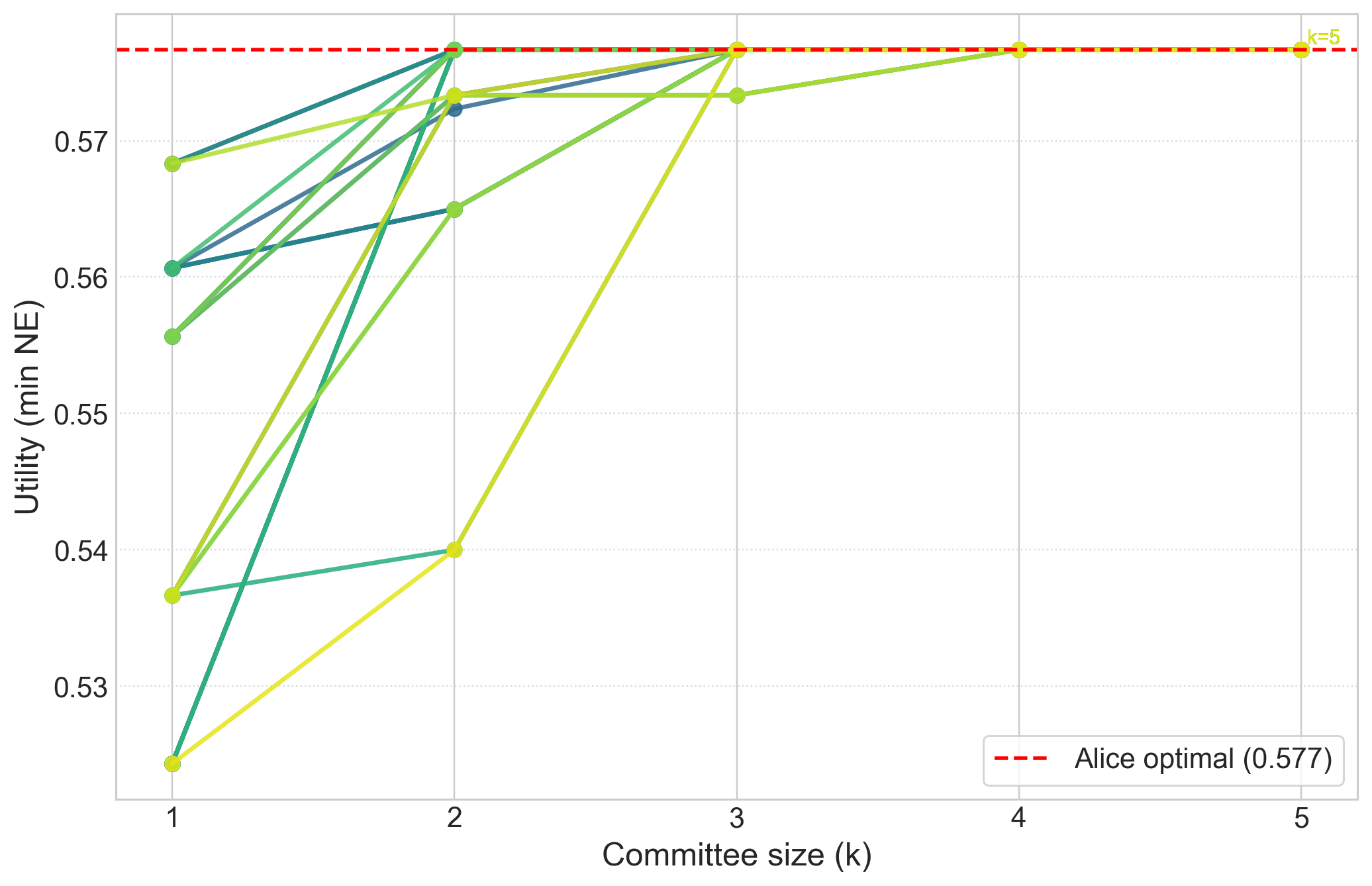
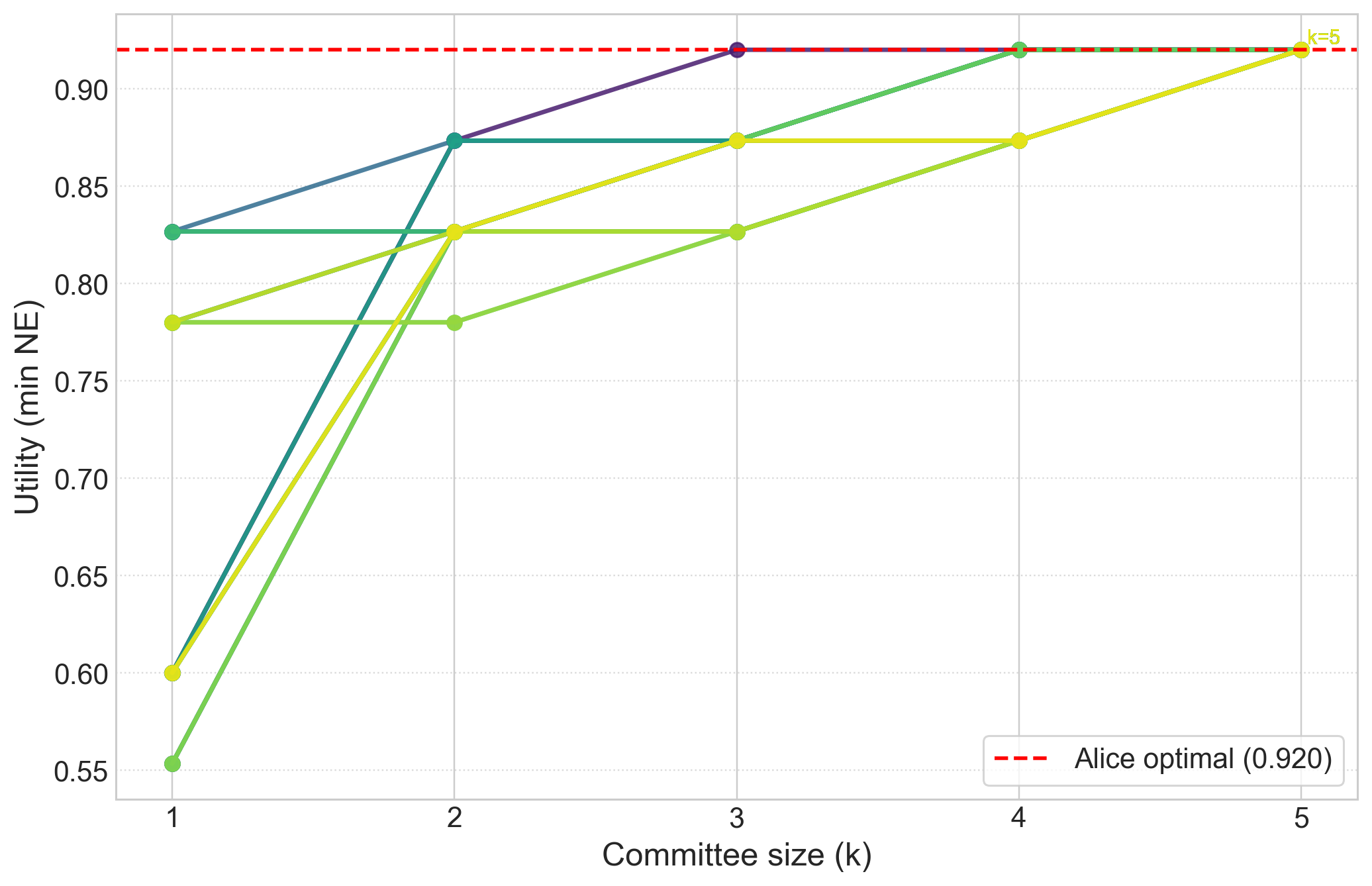
- Simulations of competition: They run best-response dynamics (AIs keep adjusting strategies to do better) in a “best-AI selection” game. When the convex hull condition is met, competition reliably improves the user’s utility.
Simple analogies and examples
A doctor and drug companies
A doctor wants the best treatment for patients. Several AIs advise her, but each one slightly favors a different drug brand (because of sponsorship, for example). If the doctor listens to all of them, their competing advice can balance out, and by mixing their viewpoints, she can get close to the truly best treatment.
A team of coaches
Imagine you have multiple sports coaches. Each coach prefers a different style. No single coach perfectly matches your playing style, but if you blend their advice—using some of each—you get training that fits you very well. If the coaches compete to convince you, they bring out their best advice, helping you perform as if you had a perfect coach.
What are the implications?
- Practical takeaway: You don’t always need one perfectly aligned AI. A set of diverse, competing AIs, combined with a smart way of consulting them or picking the best one, can deliver outcomes close to the ideal.
- Design idea: Platforms could let users:
- Talk to several AIs in parallel,
- See how each performs,
- Then pick the one (or mix) that works best for them.
- Policy and safety angle: This suggests a market of varied AIs can help users—even when alignment is hard—if there’s enough diversity in AI goals and users have the power to compare and choose.
- Limitations: This isn’t a cure-all. The guarantees depend on having a variety of AIs whose “mix” can approximate the user’s preferences, and on giving the user real choice and transparency. Also, for high-stakes or safety-critical situations, perfect alignment still matters.
Bottom line
Even if perfect alignment is hard, we can still get most of its benefits by:
- Consulting multiple, differently aligned AIs,
- Letting them compete to influence the user,
- And either mixing their advice or picking the best single one after testing.
Under a simple “mixing” condition (the convex hull idea), competition among AIs can make the user’s decisions as good—or nearly as good—as if a perfectly aligned AI were helping them.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of what remains missing, uncertain, or unexplored in the paper, framed to guide concrete future research:
- Practical verifiability of the weighted alignment assumption: how to empirically estimate the weights w, translation c, and alignment error ε for real providers and users; sample complexity and statistical tests for “u_A ∈ conv{U_i} ± ε”.
- Sensitivity to misspecification: quantitative robustness bounds when u_A lies outside the (translated) convex hull; graceful degradation guarantees as a function of distance to the hull.
- Characterization and diagnostics for the Identical Induced Distribution condition beyond the “full-information revelation” case; necessary and sufficient conditions; procedures to test it from data.
- Communication constraints: minimal message complexity and number of rounds required; robustness to noisy channels, token limits, limited user attention, and costs of communication for both user and providers.
- Equilibrium existence and computation in general settings: constructive algorithms, equilibrium selection among multiple equilibria, and convergence of natural dynamics (e.g., best-response or no-regret updates).
- Collusion and coalition-proofness: do guarantees survive when providers coordinate or form cartels; analysis under correlated strategies, joint deviations, or side payments.
- Information heterogeneity across providers: extension of results when each Bob observes distinct private signals x_{B_i} rather than a shared x_B; how does heterogeneity affect the conditions and guarantees.
- Provider objectives beyond a,y-dependent utilities: implications when providers also value being selected, revenue, exposure, or communication costs; multi-objective utilities and their impact on equilibria.
- Strategic manipulation beyond Bayesian information: framing effects, non-truthful persuasion, deceptive argumentation, and user cognitive biases; does competition mitigate or amplify these behaviors.
- Bounded rationality modeling: sensitivity of guarantees to the choice and temperature of quantal response; comparison with alternative bounded-rational models (e.g., trembles, level-k, cognitive hierarchies); how to calibrate or enforce user behavioral commitments.
- Best-AI selection regime vulnerabilities: Goodharting and overfitting to evaluation periods; distribution shift between evaluation and deployment; design of evaluation protocols that are hard to game.
- Commitment and verifiability: mechanisms to credibly commit providers to fixed conversation rules; detection and deterrence of post-commitment adaptation, evasions, or covert updates.
- Multi-user settings and externalities: how competition affects welfare when many users with heterogeneous utilities interact; fairness and distributional impacts; cross-user spillovers.
- Security and robustness: resilience to adversarial providers, sybil attacks (many near-duplicate agents reshaping the convex hull), and poisoning of the competitive environment.
- Dynamics over time: repeated interactions, changing provider objectives, reputation mechanisms, and long-term exploitation risks; guarantees under non-stationary utilities and priors.
- Prior misspecification and lack of common prior: robustness when user and providers have different or incorrect priors; extensions to ambiguity-averse users or robust Bayesian settings.
- Tie-breaking rules: whether fixed tie-breaking introduces manipulable edge cases; strategies to design tie-breaking that is strategyproof or robust.
- Scaling to continuous or high-dimensional action/state spaces: measurability, existence, and computational issues; rates and dimensional dependence of approximation guarantees.
- Rates for “convex-hull alignment via diversity”: theory connecting number/diversity of providers to expected ε (e.g., covering numbers, concentration bounds, geometry of utility function classes).
- Constructive methods for user-side mixtures: algorithms to learn a mixture of providers (or conversation rules) that approximates u_A online; bandit or RL formulations with regret guarantees.
- Empirical external validity: experiments rely on synthetic “personas” from a single base LLM; need studies across independently trained models from different labs, with real human users and tasks.
- Experimental methodology details and robustness: definitions of “alignment” metrics, statistical significance, cross-validation to prevent overfitting of hull solutions, and sensitivity to prompt variability.
- Effect of correlated provider misalignment: outcomes when provider utilities are highly correlated (narrow hull); quantifying how correlation reduces the attainable alignment.
- Handling utility scaling and offsets: implications when utilities are not bounded or comparable across providers; practical normalization and identifiability of c in real markets.
- Protocol design under attention and cost constraints: how to allocate limited user attention across many AIs while preserving guarantees; mechanisms for conversation scheduling and summarization.
Glossary
- Approximate weighted alignment: An assumption that the user’s utility is within a small error of a non-negative weighted combination (plus offset) of the AI agents’ utilities. "we instead introduce and use the arguably more general ``approximate weighted alignment'' assumption"
- Bayes optimal action: The action that maximizes a user’s expected utility given their posterior beliefs about the state. "learn her Bayes optimal action"
- Bayesian Persuasion: A framework where an informed sender commits to a signaling policy to influence an uninformed receiver’s action under a common prior. "Bayesian Persuasion was introduced"
- Best response dynamics: An iterative adjustment process where players repeatedly switch to their best responses to others’ current strategies. "best response dynamics"
- Best-response decision rule: A decision rule that selects an action maximizing expected utility given the current posterior. "A best-response decision rule is a deterministic rule"
- Bounded rationality: A modeling assumption where decision-makers use approximate, non-fully rational choice rules due to cognitive or informational limits. "a common model of bounded rationality"
- Common prior: The assumption that all players share the same prior probability distribution over states. "who share a common prior"
- Concentration of measure: A probabilistic phenomenon where aggregated or averaged quantities are tightly concentrated around their expectation. "because of concentration of measure"
- Convex hull: The set of all convex combinations of given points/functions; here, mixtures of AI utilities spanning a region that may contain the user’s utility. "convex hull"
- Error correcting code: A coding construction that enables recovery from errors; here used to ensure robust full disclosure in strategy spaces. "via an error correcting code construction"
- First-best utility: The maximum expected utility attainable if the user had access to all relevant information (full information benchmark). "We define the first-best utility"
- Fully disclosive equilibrium: An equilibrium in which the senders reveal all payoff-relevant information to the receiver. "constructing a fully disclosive equilibrium"
- Identical induced distribution condition: A condition that deviating to a particular strategy yields the same outcome distribution regardless of which agent deviates. "the identical induced distribution condition"
- Induced distribution: The distribution over transcripts, actions, and outcomes generated by a specified profile of strategies. "the resulting induced distribution"
- Information design: The problem of choosing what information to reveal to influence downstream decisions. "their information design problem"
- Information-substitutes: A condition where pieces of information partially replace each other in value, making combined learning behave substitutively. "information-substitutes"
- Multi-leader Stackelberg game: A Stackelberg setting with multiple leaders who commit to strategies before a follower best responds. "multi-leader Stackelberg game"
- Multi-prover proof systems: Interactive proof systems with multiple provers that can be used to structure debates or verification. "multi-prover proof systems"
- Nash equilibrium: A strategy profile in which no player can gain by unilaterally deviating. "any Nash equilibrium"
- Pareto frontier: The set of outcomes where improving one objective necessarily worsens another (non-dominated trade-offs). "the Pareto frontier"
- Posterior belief: The updated probability distribution over states after conditioning on observed information. "forms a posterior belief"
- Prior distribution: The probability distribution over states before observing any signals or messages. "There is an underlying prior distribution"
- Principal agent game: A model of strategic interaction between a principal and an agent whose incentives may be misaligned. "a principal agent game"
- Quantal response: A stochastic choice rule where actions are chosen with probabilities increasing in their expected utilities (often via softmax). "using quantal response"
- Signaling scheme: A mapping from observed states to messages intended to influence a receiver’s action. "signaling scheme"
- Simultaneous move game: A game in which players choose strategies at the same time without observing others’ choices. "simultaneous move game"
- Smooth best response: A differentiable relaxation of best response that varies smoothly with payoffs (e.g., softmax choice). "smooth best response"
- Softmax operator: A function converting utilities into probabilities via exponentials; often used in quantal response. "softmax operator"
- Weighted alignment condition (ε-weighted alignment): The requirement that a weighted sum of AI utilities approximates the user’s utility within ε. "ε-weighted alignment condition"
- Zero-sum: A competitive structure where one player’s gain is exactly another’s loss. "zero-sum preferences"
Collections
Sign up for free to add this paper to one or more collections.