Probabilistic and nonlinear compressive sensing (2509.15060v1)

Abstract: We present a smooth probabilistic reformulation of $\ell_0$ regularized regression that does not require Monte Carlo sampling and allows for the computation of exact gradients, facilitating rapid convergence to local optima of the best subset selection problem. The method drastically improves convergence speed compared to similar Monte Carlo based approaches. Furthermore, we empirically demonstrate that it outperforms compressive sensing algorithms such as IHT and (Relaxed-) Lasso across a wide range of settings and signal-to-noise ratios. The implementation runs efficiently on both CPUs and GPUs and is freely available at https://github.com/L0-and-behold/probabilistic-nonlinear-cs. We also contribute to research on nonlinear generalizations of compressive sensing by investigating when parameter recovery of a nonlinear teacher network is possible through compression of a student network. Building upon theorems of Fefferman and Markel, we show theoretically that the global optimum in the infinite-data limit enforces recovery up to certain symmetries. For empirical validation, we implement a normal-form algorithm that selects a canonical representative within each symmetry class. However, while compression can help to improve test loss, we find that exact parameter recovery is not even possible up to symmetries. In particular, we observe a surprising rebound effect where teacher and student configurations initially converge but subsequently diverge despite continuous decrease in test loss. These findings indicate fundamental differences between linear and nonlinear compressive sensing.

• The paper introduces a novel Exact Gradient Pruning (EGP) method that reformulates ℓ0-regularized regression into a differentiable, efficiently optimizable framework.
• EGP achieves orders of magnitude faster convergence and improved reconstruction accuracy compared with traditional Monte Carlo and classical methods across various signal-to-noise regimes.
• For nonlinear models, the paper extends compressive sensing to neural network sparsification, revealing the ℓ2 rebound phenomenon during teacher-student parameter recovery.

Probabilistic and Nonlinear Compressive Sensing: Theory, Algorithms, and Empirical Analysis

Introduction

This paper presents a rigorous reformulation and extension of compressive sensing, focusing on both linear and nonlinear regimes. The authors introduce Exact Gradient Pruning (EGP), a smooth probabilistic approach to $\ell_0$-regularized regression that circumvents the need for Monte Carlo sampling, enabling efficient and exact gradient computation. The work further explores nonlinear generalizations, particularly in the context of neural network sparsification and teacher-student parameter recovery, and provides both theoretical guarantees and empirical evidence for the strengths and limitations of these methods.

Probabilistic Reformulation of $\ell_0$ Regularized Regression

The central technical contribution is the derivation of a closed-form, differentiable surrogate for the combinatorial $\ell_0$ regularized regression objective. The classical problem is:

$$\min_{\theta \in \mathbb{R}^p} \|y - F\theta\|_2^2 + \lambda \ell_0(\theta)$$

where $\ell_0(\theta)$ counts the number of nonzero entries in $\theta$. Previous probabilistic reformulations required Monte Carlo sampling over binary masks, resulting in high variance and slow convergence. The authors prove that, for quadratic objectives, the expectation over Bernoulli masks can be computed in closed form, yielding the EGP objective:

$$\min_{w \in \mathbb{R}^p, \gamma \in [0,1]^p} \|y - F(w\gamma)\|_2^2 + \sum_{i,j} F_{ij}^2 w_j^2 \gamma_j (1-\gamma_j) + \lambda \sum_i \gamma_i$$

This enables direct application of SGD and related optimizers, leveraging GPU acceleration and parallelization. The method is trivially extensible to include $\ell_1$ and $\ell_2$ regularization, with all terms remaining piecewise differentiable.

Empirical Comparison: EGP vs. Monte Carlo and Classical Methods

The authors conduct extensive empirical comparisons between EGP, Monte Carlo-based probabilistic methods (Reinforce, DisARM, BitFlip-1, UGC), and established compressive sensing algorithms (Lasso, Relaxed Lasso, Forward Stepwise, IHT). EGP demonstrates orders of magnitude faster convergence and superior reconstruction accuracy across a wide range of problem sizes and signal-to-noise ratios.

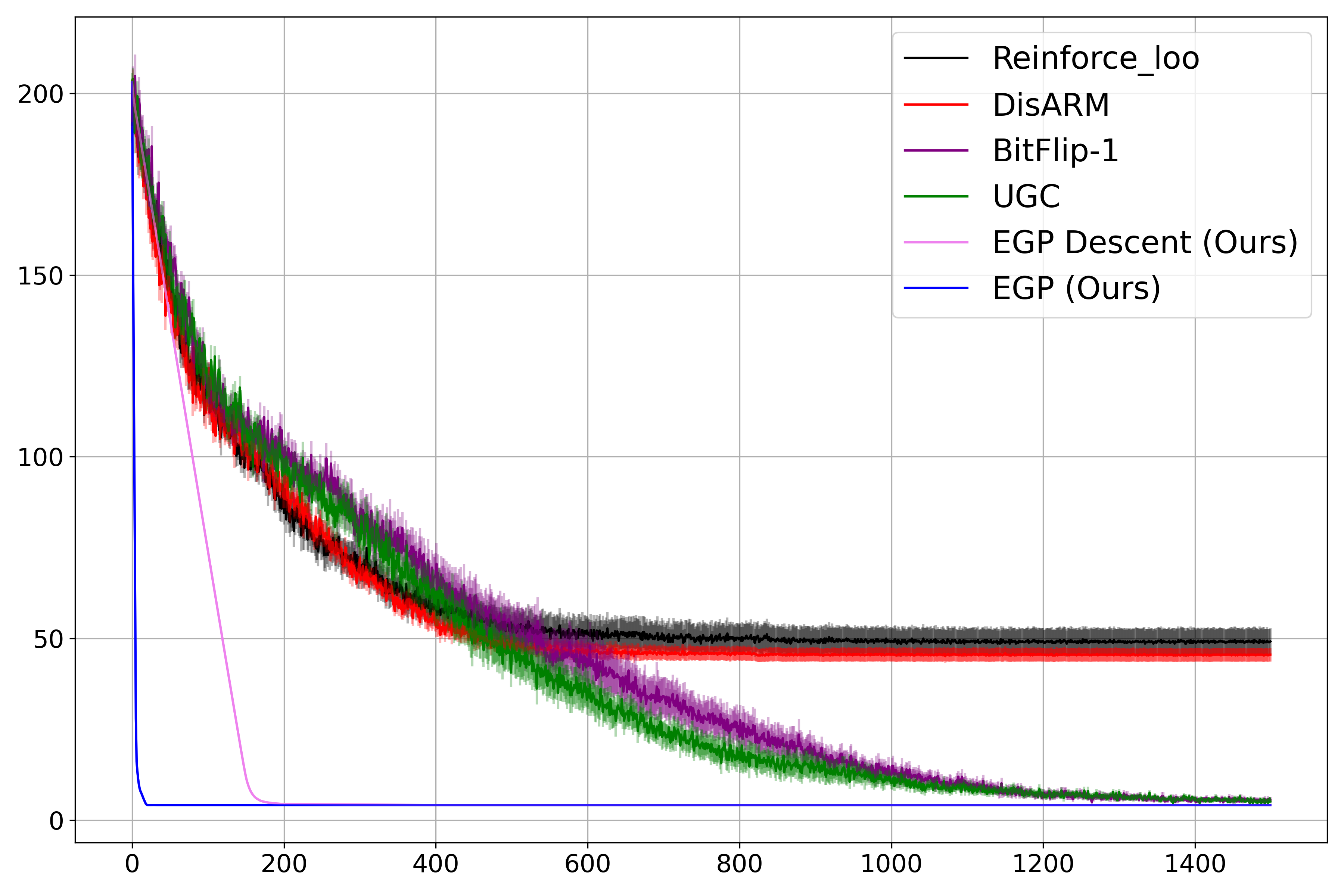
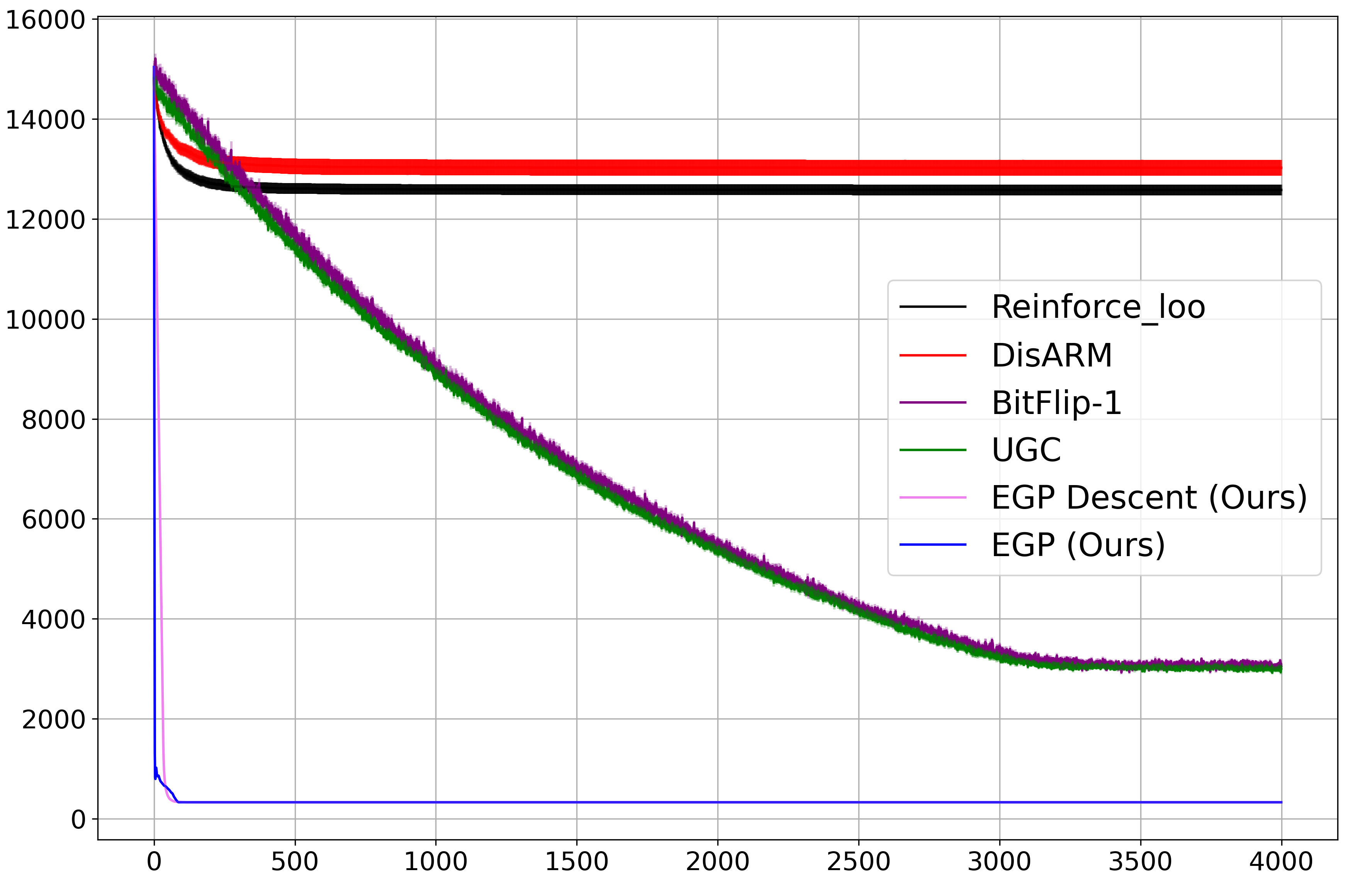
Figure 1: Convergence speed comparison of EGP with Monte Carlo methods for two settings, showing EGP's rapid and stable loss reduction.

EGP's runtime scales linearly with both sample size and parameter dimension, and its performance is robust to hyperparameter choices. In contrast, Monte Carlo methods suffer from high variance, slow convergence, and poor scalability, especially in high-dimensional settings.

Systematic Benchmarks: Signal-to-Noise and Correlation Effects

The paper systematically benchmarks EGP against Lasso, Relaxed Lasso, Forward Stepwise, and IHT across multiple regimes of signal-to-noise ratio (SNR) and feature correlation. EGP consistently achieves lower relative test error (RTE) and active set reconstruction error (ASRE), particularly in high-SNR and high-dimensional settings.

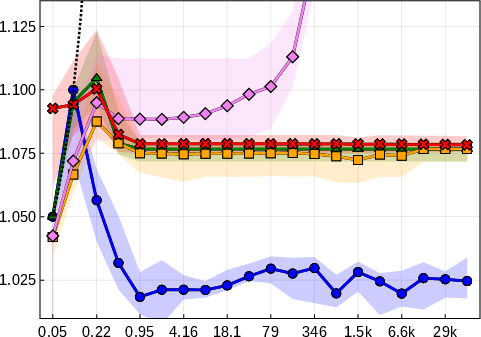
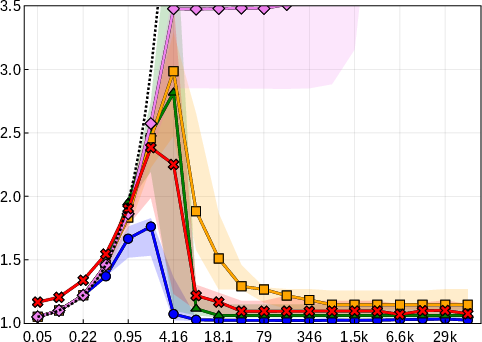
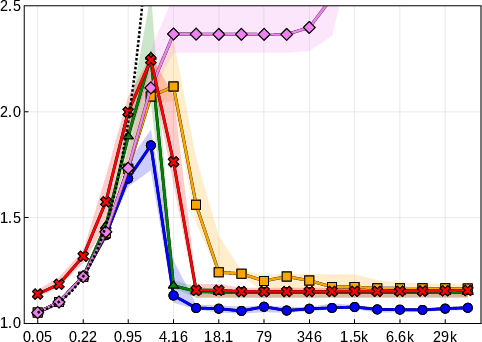
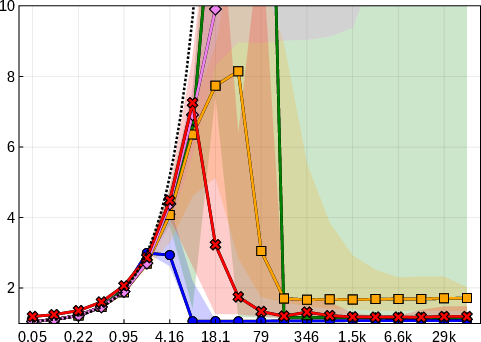
Figure 2: RTE as a function of SNR for four benchmark settings, demonstrating EGP's superior generalization across regimes.

EGP's active set recovery is notably more accurate than Lasso and Relaxed Lasso, which suffer from shrinkage bias and incomplete support recovery even at high SNR. Forward Stepwise and IHT are less competitive in low-SNR and high-correlation scenarios.

Nonlinear Compressive Sensing and Neural Network Sparsification

The authors extend compressive sensing theory to nonlinear models, focusing on neural networks. They formalize the connection between regularized regression and the minimum description length principle, generalizing the objective to:

$$L_\lambda(\theta) = \lambda \ell_0(\theta) + \frac{1}{2}\log_2(2\pi\sigma^2) + \frac{\|y - F_\theta(x)\|_2^2}{2\sigma^2 \ln(2)}$$

where $F_\theta$ may be a nonlinear function, such as an MLP. Theoretical analysis, building on Fefferman-Markel results, shows that in the infinite-data limit, parameter recovery is possible up to network symmetries (permutations and sign flips).

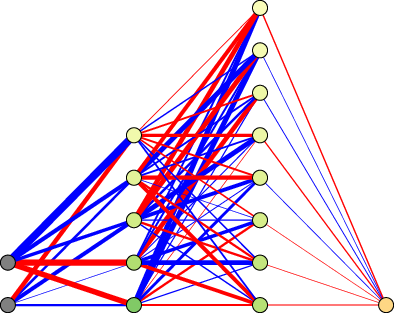
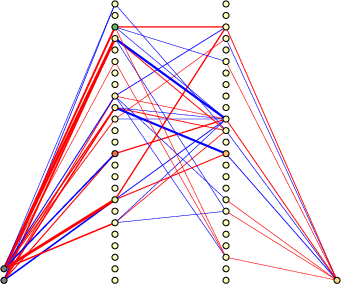
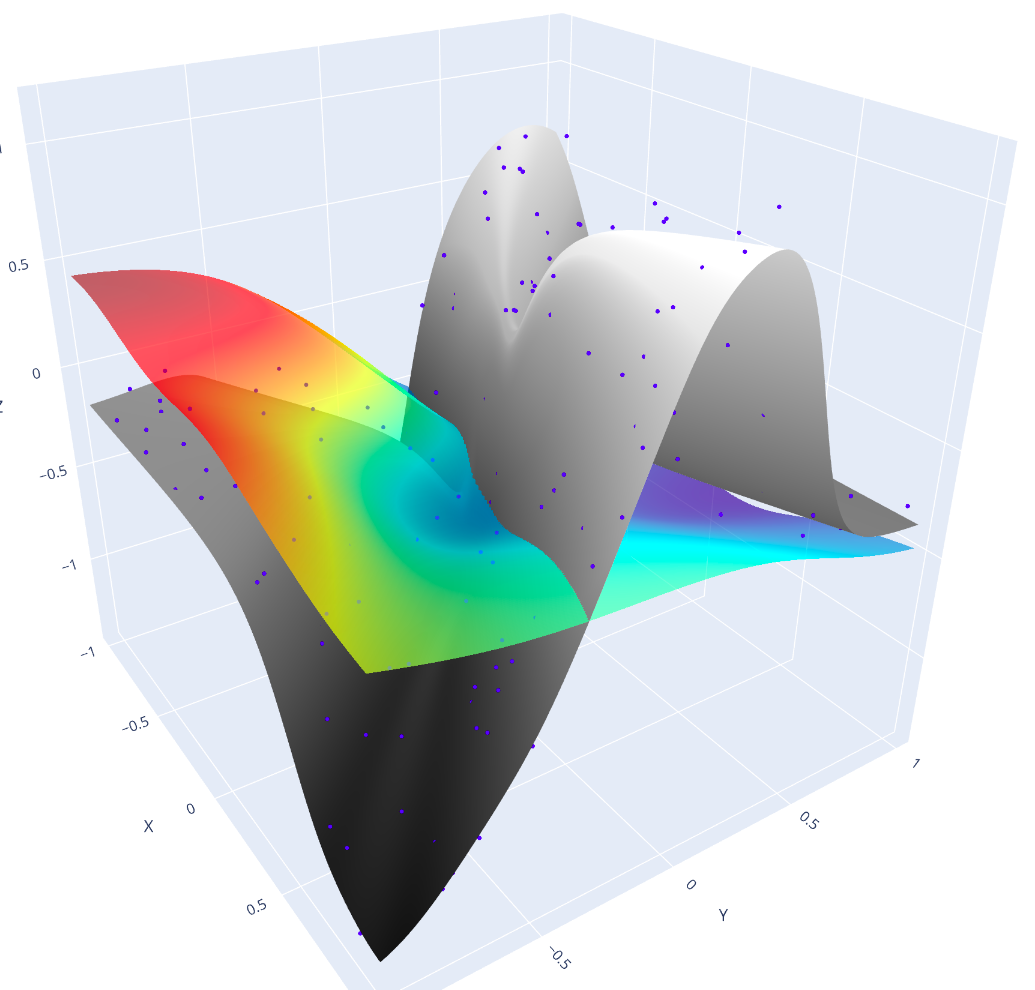
Figure 3: (a) Typical teacher network. (b) Pruned student network. (c) Teacher function (grey), student function (rainbow color, before training), and teacher-generated training dataset (blue dots).

Teacher-Student Experiments: Parameter Recovery and the $\ell_2$ Rebound Phenomenon

Empirical teacher-student experiments reveal a contradictory phenomenon: while regularization improves test loss and functional approximation, exact parameter recovery—even up to symmetries—is not achieved in practice. The authors observe a surprising $\ell_2$ rebound effect: student parameters initially converge toward the teacher but subsequently diverge, despite continuous improvement in test loss.

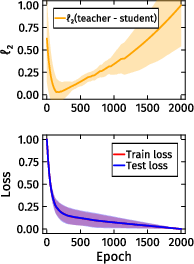
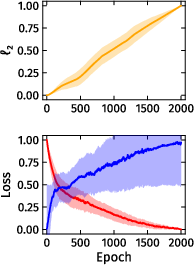
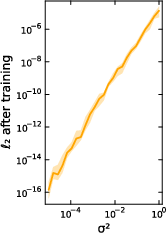
Figure 4: The $\ell_2$ rebound phenomenon in teacher-student parameter recovery: initial convergence followed by divergence, even as loss decreases.

This decoupling of functional and parametric convergence highlights a fundamental difference between linear and nonlinear compressive sensing. The optimization landscape for nonlinear models is highly non-convex, and gradient-based methods tend to find functionally equivalent but structurally distinct solutions.

Practical Implications and Theoretical Outlook

EGP provides a scalable, efficient, and accurate method for sparse regression and compressive sensing, with immediate applicability to high-dimensional data analysis, neural network pruning, and scientific modeling. Its integration into deep learning frameworks is straightforward due to its reliance on standard optimization primitives.

Theoretical results suggest that, while functional recovery is possible in nonlinear models, parameter identifiability remains elusive for finite datasets and practical optimization. This has implications for interpretability, model compression, and the design of sparse neural architectures.

Conclusion

The paper establishes EGP as a state-of-the-art method for $\ell_0$-regularized regression, outperforming both Monte Carlo-based probabilistic approaches and classical compressive sensing algorithms in speed and accuracy. The extension to nonlinear models is theoretically sound but empirically limited by the non-convexity of the optimization landscape. The observed $\ell_2$ rebound phenomenon underscores the need for new theoretical and algorithmic tools to address parameter recovery in nonlinear settings. Future research directions include genome-wide association studies, neural ODE/PDE pruning, and deeper analysis of the optimization landscape in overparameterized models.