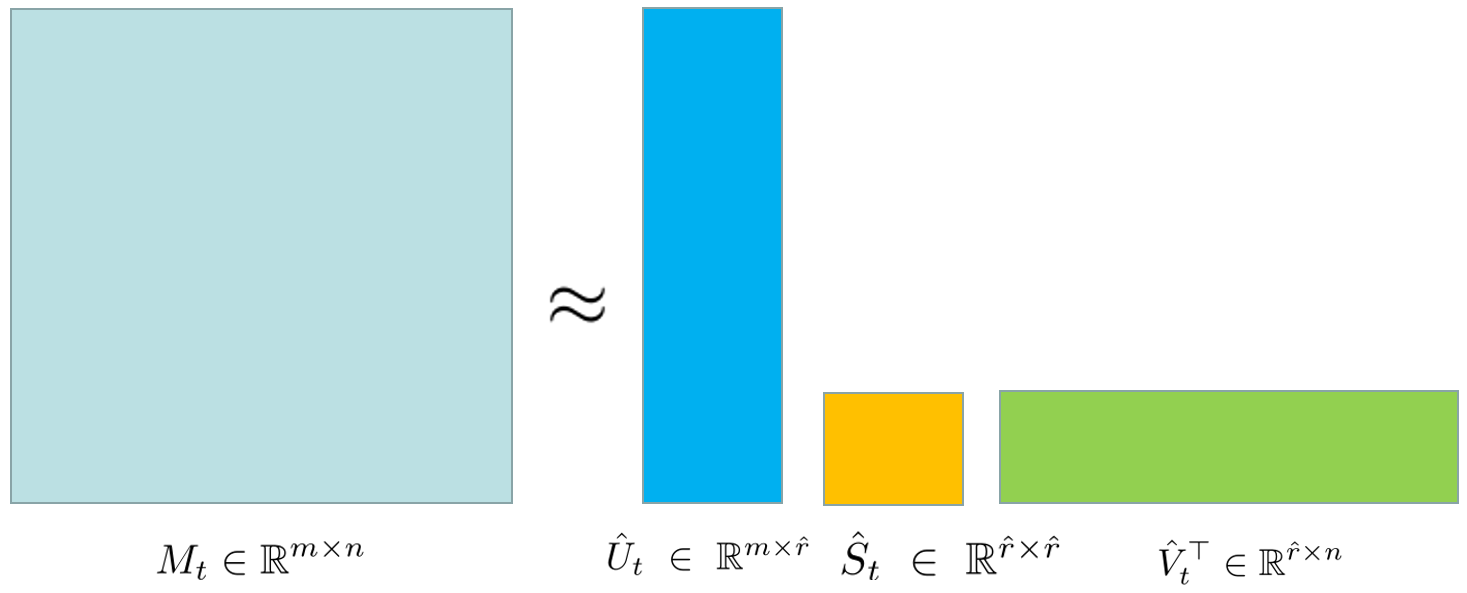LiMuon: Light and Fast Muon Optimizer for Large Models (2509.14562v1)
Abstract: Large models recently are widely applied in artificial intelligence, so efficient training of large models has received widespread attention. More recently, a useful Muon optimizer is specifically designed for matrix-structured parameters of large models. Although some works have begun to studying Muon optimizer, the existing Muon and its variants still suffer from high sample complexity or high memory for large models. To fill this gap, we propose a light and fast Muon (LiMuon) optimizer for training large models, which builds on the momentum-based variance reduced technique and randomized Singular Value Decomposition (SVD). Our LiMuon optimizer has a lower memory than the current Muon and its variants. Moreover, we prove that our LiMuon has a lower sample complexity of $O(\epsilon{-3})$ for finding an $\epsilon$-stationary solution of non-convex stochastic optimization under the smooth condition. Recently, the existing convergence analysis of Muon optimizer mainly relies on the strict Lipschitz smooth assumption, while some artificial intelligence tasks such as training LLMs do not satisfy this condition. We also proved that our LiMuon optimizer has a sample complexity of $O(\epsilon{-3})$ under the generalized smooth condition. Numerical experimental results on training DistilGPT2 and ViT models verify efficiency of our LiMuon optimizer.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces LiMuon, a new way to train very large AI models (like language or vision models) faster and with less memory. It improves on a recent optimizer called Muon, which is designed for parameters that naturally form matrices (grids of numbers). LiMuon keeps Muon’s good ideas but uses smarter tricks so it needs less memory and reaches good solutions in fewer training steps.
Objectives
The researchers wanted to answer three simple questions:
- Can we make Muon lighter on memory so it’s easier to train big models on regular GPUs?
- Can we make Muon reach good solutions faster, using fewer data samples or steps?
- Can we prove it works under realistic conditions (not just perfect mathematical assumptions) that better match how large AI models are trained?
Methods and Approach
To understand LiMuon, it helps to know what an “optimizer” does. When training a model, the optimizer decides how to change the model’s parameters to make its predictions better. Muon is special because it treats parameters as matrices and updates them using an “orthogonal” direction, which often stabilizes training.
LiMuon builds on Muon with two key ideas: 1) Momentum-based variance reduction (like STORM): - Imagine pushing a grocery cart down a bumpy road. The bumps (random noise in gradients) make it wobbly. Momentum reduces wobble by carrying forward a smoothed version of your push. - Variance reduction carefully corrects this momentum using fresh information so the “push” stays accurate even with noise. This helps the optimizer stay on track with fewer samples.
2) Randomized SVD (RSVD) to save memory: - SVD (Singular Value Decomposition) breaks a big matrix into simpler parts (think: taking a large LEGO build apart into a few key shapes). It’s a way to find the most important directions in the matrix. - Randomized SVD does this approximately and much faster by sampling smart “random directions.” - LiMuon uses RSVD to store a compressed version of its momentum (the “push history”), keeping only the most important parts. This drastically reduces memory use while keeping updates effective.
LiMuon offers two practical options:
- Option #1: Use momentum with variance reduction (fast and accurate). It keeps full momentum matrices, so it doesn’t save memory as much.
- Option #2: Compress the momentum with RSVD (low memory). It stores only a small number of columns and singular values, not the whole big matrix, so it uses much less memory. It’s still accurate enough for training large models.
What do these terms mean in everyday language?
- Matrix parameters: Many parts of neural networks are naturally grids of numbers (matrices) or stacks of grids (tensors).
- Orthogonal update: Choosing a direction that’s “balanced” and well-behaved, so updates don’t blow up or get stuck.
- Momentum: Like pushing a cart—each new push adds to the previous, smoothing the ride.
- Variance reduction: Adjusting that push to cancel out random bumps (noise).
- SVD/RSVD: Breaking a big block into simpler pieces, keeping only the pieces that matter most to save memory and time.
Main Findings
The paper shows several important results:
- Lower memory use: LiMuon’s Option #2 stores a compressed momentum using RSVD, reducing memory from roughly “size of full matrices” to “size of a few columns.” In simple terms, it needs much less GPU memory during training.
- Faster convergence in theory:
- To get “error” down to ε (a small number), you need about 1/(ε³) samples or steps.
- This beats earlier Muon analyses that needed O(ε⁻⁴), i.e., more steps.
- Works under more realistic conditions: Earlier proofs assumed very strict smoothness (like perfectly gentle hills on the loss landscape). LiMuon’s theory also works under “generalized smoothness,” which better matches how real AI models behave (sometimes the hills are steeper or uneven).
- Real-world experiments:
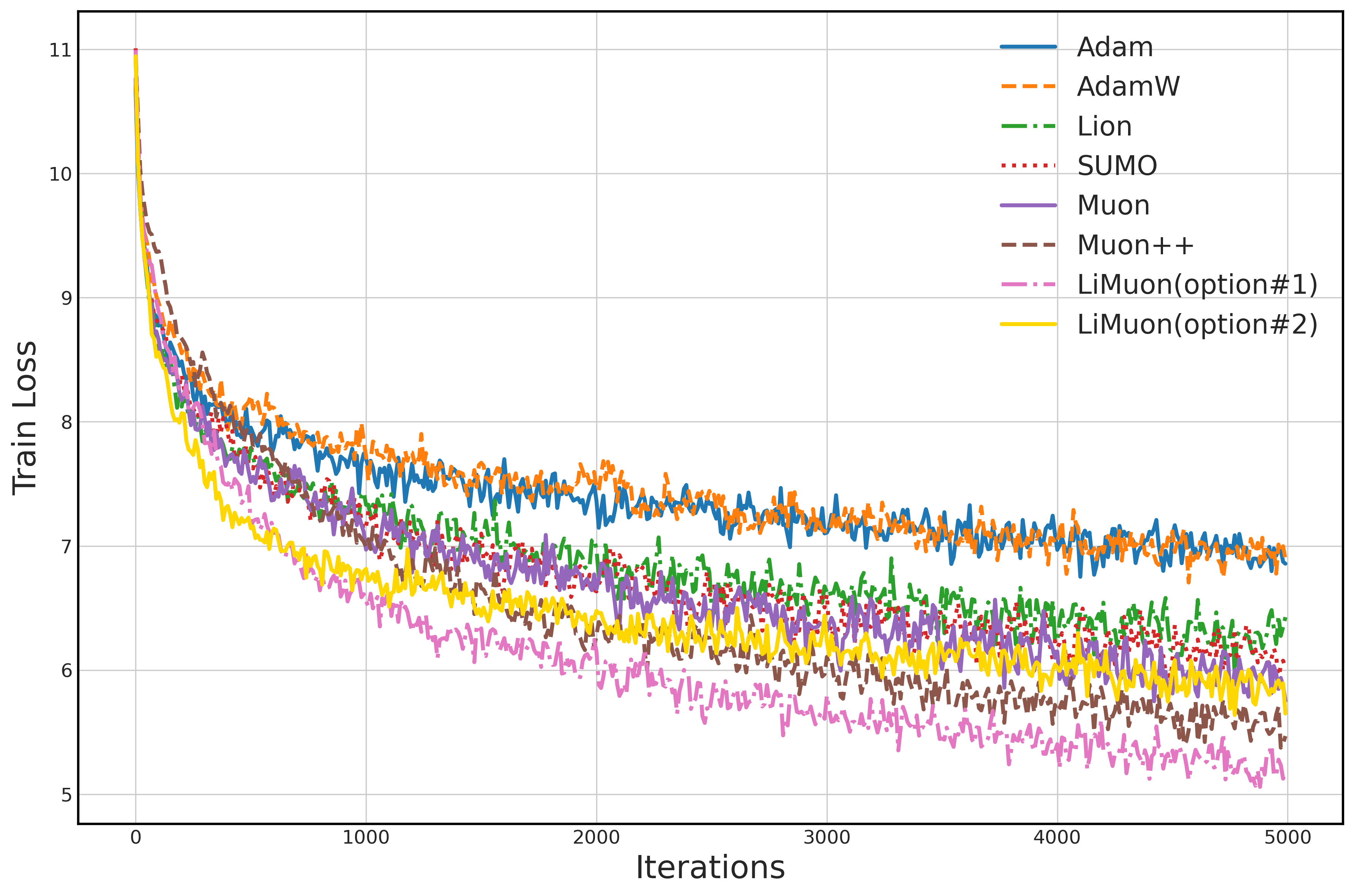
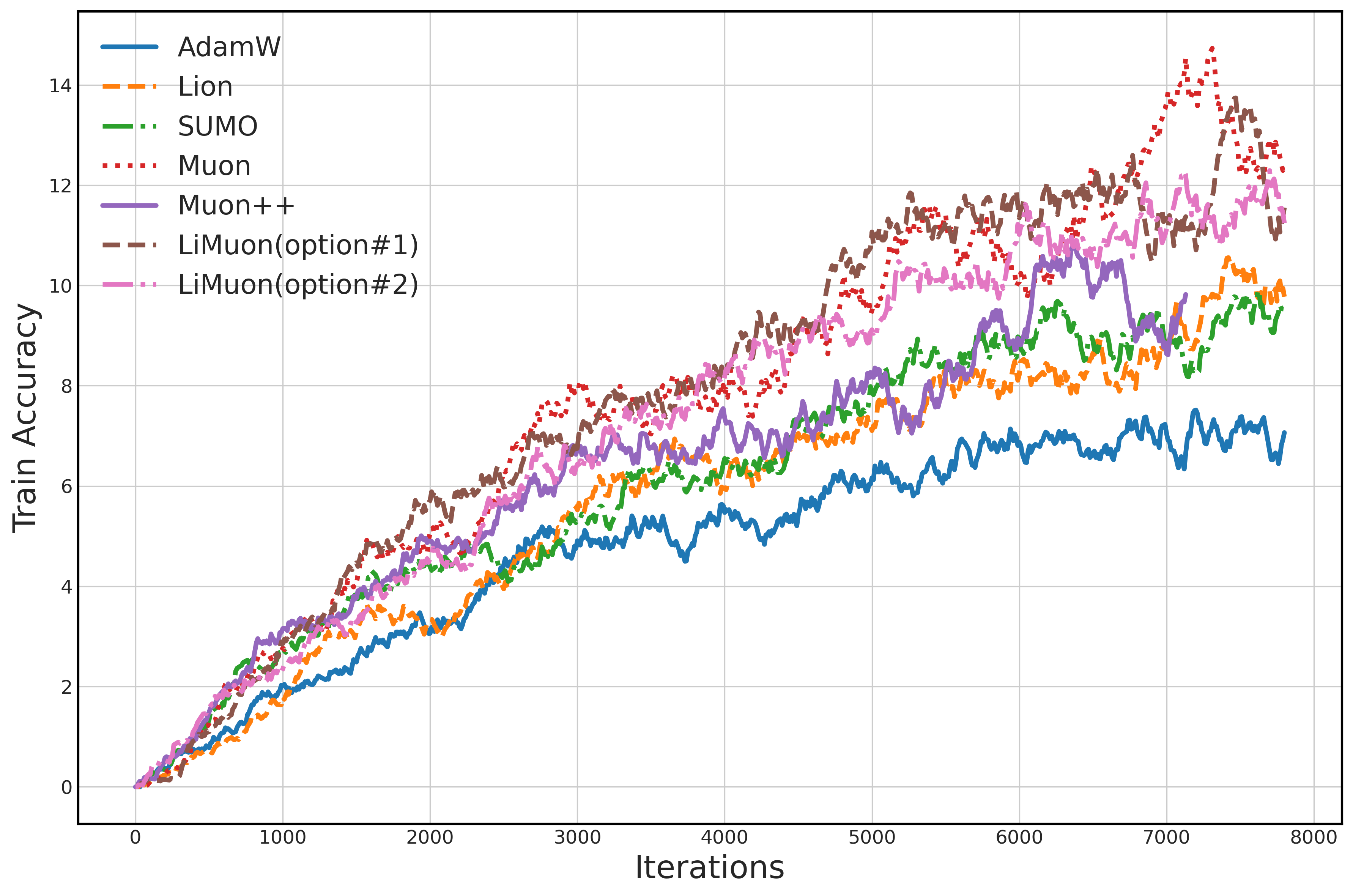
- On DistilGPT2 (a smaller GPT-2), trained on WikiText-103:
- LiMuon Option #1 achieved lower perplexity (meaning it predicts text better) than AdamW, Lion, SUMO, Muon, and Muon++.
- LiMuon Option #2 still performed well and used less memory.
- On ViT (Vision Transformer), trained on Tiny ImageNet:
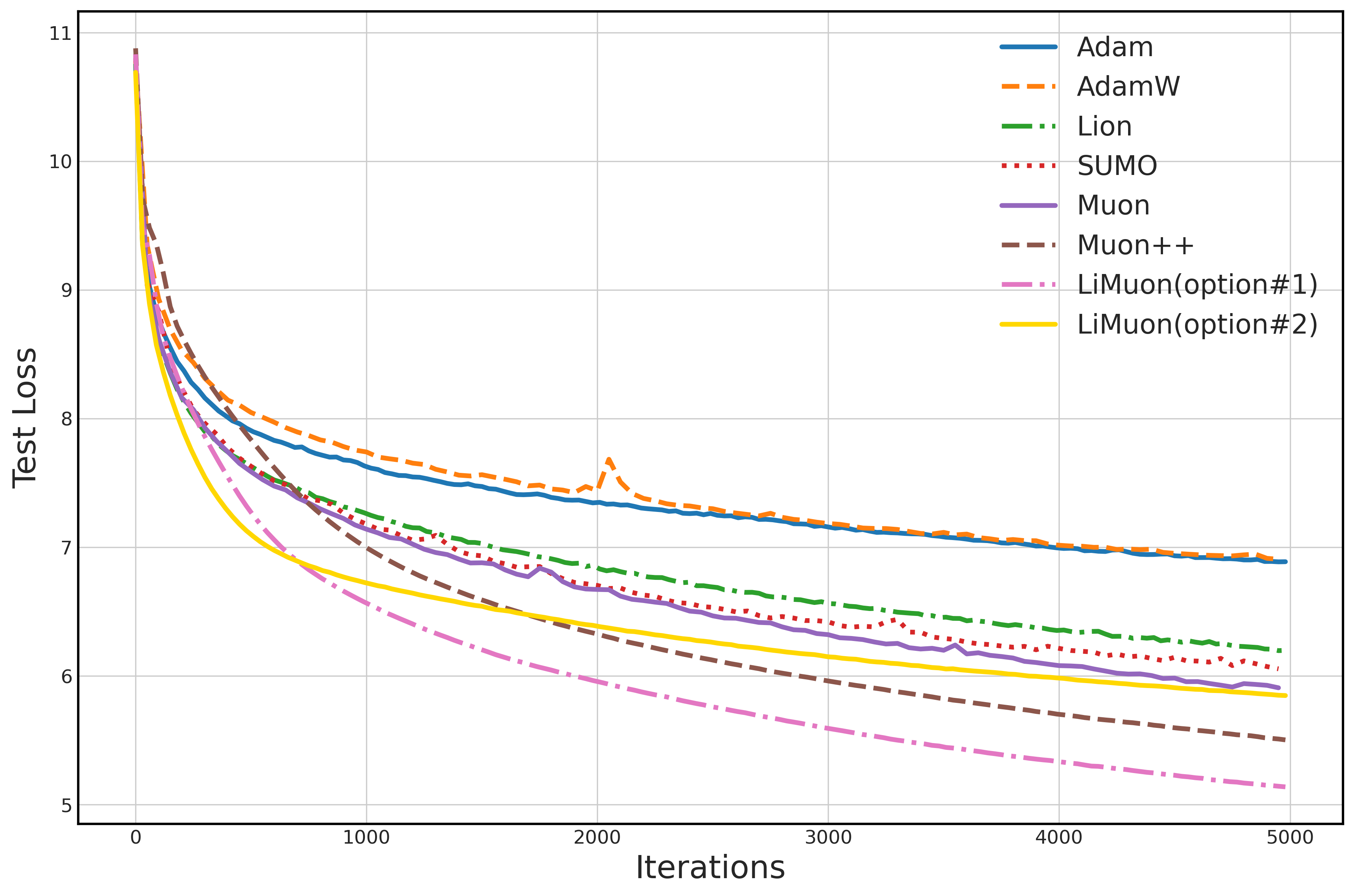
- LiMuon converged faster (training loss dropped quicker) and had better validation loss compared to others.
- Option #2 used the least memory, showing strong practical benefits.
These results suggest LiMuon is both efficient and effective for training large models on standard hardware.
Implications and Impact
Why this matters:
- Training big AI models is expensive, slow, and memory-hungry. An optimizer that uses less memory and reaches good solutions faster can save costs and make large-model training more accessible.
- LiMuon’s combination of smarter momentum (variance reduction) and compressed storage (RSVD) enables training on GPUs with limited memory without sacrificing performance much.
- Since it works under more realistic assumptions, LiMuon’s theory is more relevant to real-world tasks like LLMs, not just idealized math scenarios.
In short, LiMuon could help researchers and engineers train big models more efficiently, making advanced AI more practical and affordable.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, consolidated list of what remains missing, uncertain, or unexplored in the paper, phrased to be directly actionable for follow-up work:
- Clarify and validate the memory model: peak GPU memory vs. persistent optimizer state. The paper claims reduced “state memory,” yet RSVD(M_t) is computed from the full M_t each step—does this require storing M_t transiently, and how does that affect true peak memory in practice across layers and model scales?
- Provide wall-clock performance analysis. The theoretical SFO improvement does not guarantee faster training. Quantify per-step runtime, throughput, and total time-to-target across Muon, LiMuon(#1), LiMuon(#2), and Muon++ on realistic model sizes.
- Characterize the computational overhead of SVD/RSVD/Newton–Schulz per layer. Report FLOPs and latency for orthogonalization and momentum compression, and identify when RSVD is beneficial vs. when it becomes the bottleneck.
- Analyze convergence with approximate orthogonalization. Current proofs assume exact orthogonalization via SVD; provide guarantees under finite-iteration Newton–Schulz or RSVD-based orthogonalization errors in both Lipschitz and generalized smooth settings.
- Develop adaptive rank selection strategies. The theory for Option #2 requires γ ≤ β/(c√r(1−β)), linking rank , oversampling s, and spectral tail parameter ρ. Propose and test procedures to (i) estimate ρ online, (ii) choose and s per layer/step to satisfy the bound while minimizing memory.
- Empirically validate the low-rank momentum assumption. Measure the spectral decay of M_t across layers and training time to justify Assumption 5 (tail singular values bounded relative to gradient norm) and quantify typical ρ in modern LLMs/ViTs.
- Extend theory to tensor-structured parameters. The method and analysis focus on matrices; formalize and analyze tensor variants (e.g., Tucker/TT decompositions) for convolutional and multi-dimensional layers.
- Assess robustness to mixed precision and numerical stability. Provide results with float16/bfloat16, quantify sensitivity of RSVD/QR to precision, and analyze error accumulation in long runs.
- Hyperparameter sensitivity and scheduling. The proofs require ; experiments use fixed values. Explore schedules vs. constants, report sensitivity curves for , , and s, and offer practical tuning guidance.
- Interplay with gradient clipping and heavy-tailed noise. Many large-model trainings clip gradients and exhibit heavy-tailed noise; extend analysis beyond bounded variance, and test with/without clipping.
- Interaction with weight decay and norm constraints. Muon variants have connections to spectral norm constraints and decoupled weight decay; analyze whether LiMuon preserves or alters these properties and how to best combine them.
- Generalized smoothness realism. The paper assumes -smoothness but does not verify whether typical loss landscapes satisfy it. Estimate empirically or relax assumptions to more realistic conditions (e.g., Hölder continuity, local smoothness).
- Empirical validation of sample complexity. The O(ε{-3}) result is not corroborated by experiments that vary ε; design experiments that track accuracy/gradient norm vs. number of SFOs to test scaling laws.
- Broader and stronger baselines. Include AdaFactor, Adagrad, Shampoo (matrix/tensor preconditioners), K-FAC, and recent memory- or structure-aware optimizers to strengthen the empirical comparison.
- Larger-scale evaluations. Results are on DistilGPT2 and Tiny-ImageNet ViT; test on larger LLMs/ViTs, longer training horizons, and real-world fine-tuning tasks to assess scalability and stability.
- Layerwise heterogeneity. Investigate per-layer rank choices, different β per layer, and whether certain layers benefit more from low-rank momentum than others.
- Effect on generalization. Low-rank momentum may bias the update geometry; measure its impact on generalization, calibration, and robustness (e.g., OOD, adversarial).
- Communication and distributed training costs. Analyze how LiMuon interacts with data/tensor parallelism, optimizer state sharding, and communication overhead for U, S, V factors.
- Memory–accuracy trade-offs. Provide systematic ablations over and s to map the frontier between memory savings, convergence speed, and final performance.
- Stability under non-i.i.d. and curriculum/packing strategies. Extend theory and tests to non-i.i.d. sampling regimes common in large-scale pretraining (packing, curriculum, replay).
- Convergence constants and dependence on r. The bounds have explicit dependence on r = min(m, n); investigate whether this dependence can be reduced, and compare with other structured optimizers’ constants.
- Practical guidance for choosing orthogonalization method. Offer decision criteria for when to use SVD vs. Newton–Schulz vs. RSVD for the update step itself (line 4), including error–cost trade-offs and their effect on convergence.
- Code availability and reproducibility. Provide open-source implementation with reproducible scripts, seeds, and logging to validate memory claims and performance across settings.
- Compatibility with common training tricks. Evaluate with gradient accumulation, activation checkpointing, ZeRO-style optimizer partitioning, and mixed-precision loss scaling to ensure practical deployability.
- Monitoring and diagnostics for spectral tails. Introduce tools to monitor per-layer singular value tails of M_t online to inform adaptive rank decisions and detect when Option #2 could harm convergence.
- Theoretical treatment of compounded randomness. Analyze how RSVD randomness interacts with stochastic gradient noise (two noise sources), and its effect on bias/variance of M_{t+1}.
- Applicability beyond Frobenius/nuclear-norm criteria. Explore convergence in terms of other gaps (e.g., Frank-Wolfe gap, KKT conditions) under the LiMuon updates, aligning with recent Muon analyses.
Glossary
- Adam: An adaptive gradient optimization algorithm that estimates first-order and second-order moments of gradients to adjust learning rates. "Recently, adaptive gradient methods such as Adam~\citep{kingma2014adam}"
- AdamW: A variant of Adam that decouples weight decay from the gradient update to improve generalization. "and AdamW~\citep{loshchilov2017decoupled} have become standard choice for training large-scale models"
- Attention mechanisms: Neural network components that compute weighted combinations of inputs (queries, keys, values) to focus on relevant information. "attention mechanisms~\citep{vaswani2017attention}"
- Bounded variance: An assumption that the variance of the stochastic gradient estimator is finite and bounded by a constant. "Bounded Variance"
- Conditional gradient (Frank-Wolfe): An optimization method that uses linear minimization oracles over constraint sets (norm-balls) instead of projections. "stochastic conditional gradient (a.k.a., stochastic Frank-Wolfe)~\citep{hazan2016variance}"
- Decoupled weight decay: A regularization technique where weight decay is applied separately from the gradient-based update rule. "the Muon with decoupled weight decay implicitly solves an optimization problem that enforces a constraint on the spectral norm of weight matrices."
- DistilGPT2: A distilled (smaller) version of GPT-2 used for LLMing tasks. "train the DistilGPT2 on the wikitext-103 dataset~\citep{merity2016pointer}"
- Frank-Wolfe gap: A measure of optimality in Frank-Wolfe algorithms indicating progress toward a solution. "established its convergence guarantees in terms of the Frank-Wolfe gap, which implies convergence to a KKT point"
- Frobenius inner product: The matrix inner product defined as the trace of the product of one matrix transpose and another. "the Frobenius inner product defined as "
- Frobenius norm: The norm of a matrix defined as the square root of the sum of squares of its entries. "the Frobenius norm defined as "
- Frobenius-norm Lipschitz smoothness: A smoothness condition where gradient differences are bounded in Frobenius norm by a Lipschitz constant times the parameter difference. "are -Frobenius norm Lipschitz smooth"
- Generalized gradient norm clipping (GGNC): Methods that clip gradients under generalized smoothness to stabilize training. "studied the convergence properties of the generalized gradient norm clipping methods under the -smoothness~\citep{zhang2019gradient}."
- Generalized smooth condition: A relaxed smoothness assumption characterized by parameters allowing gradient Lipschitz constants to depend on gradient norms. "under the generalized smooth condition."
- KKT point: A point satisfying Karush–Kuhn–Tucker conditions, indicating stationarity under constraints. "which implies convergence to a KKT point of the Muon under a norm constraint"
- LiMuon optimizer: A light and fast variant of the Muon optimizer using momentum-based variance reduction and randomized SVD. "To fill this gap, we propose a light and fast Muon (LiMuon) optimizer"
- Linear Minimization Oracle (LMO): An oracle that returns a point minimizing a linear function over a constraint set. "by leveraging the linear minimization oracle (LMO) over a norm-ball"
- Low-rank approximated estimate: An approximation of a matrix using a small number of singular components to reduce memory. "is a low-rank approximated estimate of momentum ."
- Muon optimizer: A matrix-gradient optimizer that orthogonalizes gradient momentum, often via Newton–Schulz iterations. "A typical noteworthy optimization algorithm is the Muon optimizer~\citep{jordanmuon}"
- Muon: A variant of the Muon optimizer analyzed under Frank-Wolfe frameworks and showing improved complexity under large batch sizes. "Muon~\citep{sfyraki2025lions}"
- Newton–Schulz iterations: Iterative method to approximate matrix functions (e.g., orthogonalization) without explicit SVD. "Newton-Schulz iterations~\citep{jordanmuon,bernstein2024old} to approximate the orthogonalization process."
- Non-Euclidean trust-region gradient method: An optimization method using trust regions defined under non-Euclidean geometries. "studied the convergence properties of the stochastic non-Euclidean trust-region gradient method with momentum"
- Nuclear norm: The sum of singular values of a matrix, used as a convex surrogate for rank. " denotes its nuclear norm."
- Nuclear-norm stationary point: A stationarity notion measured with respect to the nuclear norm of the gradient. "for finding an -nuclear-norm stationary point of nonconvex stochastic optimization."
- Orthogonalization process: The procedure to produce an orthogonal (or orthonormal) matrix from gradients or momentum. "to approximate the orthogonalization process."
- Orthogonalized gradient momentum: A technique that orthogonalizes momentum directions before applying updates to matrix parameters. "updates matrix parameters with orthogonalized gradient momentum using Newton-Schulz iteration."
- Oversampling parameter: An RSVD parameter controlling extra sampled dimensions beyond target rank to improve approximation quality. "oversampling parameter "
- Preconditioning perspective: Viewing optimizers as applying transformations to gradients to improve conditioning and convergence. "showed that the Muon is a class of matrix-gradient optimizers from a unifying preconditioning perspective."
- QR decomposition: Factorization of a matrix into an orthonormal matrix Q and an upper-triangular matrix R. "compute the QR decomposition "
- Randomized Singular Value Decomposition (RSVD): A probabilistic algorithm that computes low-rank SVD approximations efficiently. "RSVD()"
- Sample complexity: The number of stochastic gradient samples required to achieve a target accuracy. "has a lower sample complexity of "
- Singular Value Decomposition (SVD): Matrix factorization into singular vectors and singular values, used for orthogonalization and low-rank structures. ""
- Spectral norm: The largest singular value of a matrix, measuring its maximum amplification of a vector. "a constraint on the spectral norm of weight matrices."
- SFO (Stochastic First-order Oracle) complexity: Complexity measured by the number of stochastic gradient calls. "has a Stochastic First-order Oracle (SFO) complexity of "
- STORM: A momentum-based variance reduction method for stochastic optimization. "the momentum-based variance reduced technique of STORM~\citep{cutkosky2019momentum}"
- Subspace-aware moment-orthogonalization (SUMO): An optimizer that orthogonalizes momentum in a low-dimensional subspace to reduce memory. "a subspace-aware moment-orthogonalization (SUMO) optimizer."
- Variance reduction: Techniques that reduce the variance of stochastic gradient estimates to improve convergence rates. "momentum-based variance reduced technique"
- ViT: Vision Transformer, a transformer-based model for image classification using patch embeddings. "training DistilGPT2 and ViT models"
- Weight decay: L2 regularization applied to parameters during optimization to prevent overfitting. "the Muon with weight decay can be viewed as special instances of a stochastic Frank-Wolfe algorithm"
Collections
Sign up for free to add this paper to one or more collections.