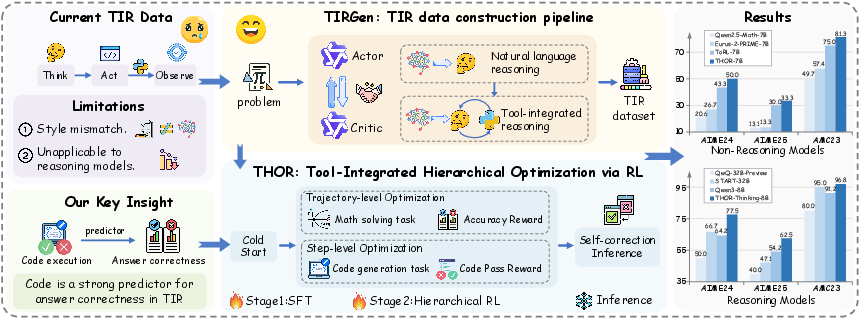
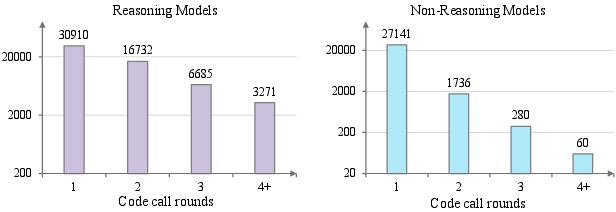THOR: Tool-Integrated Hierarchical Optimization via RL for Mathematical Reasoning (2509.13761v1)
Abstract: LLMs have made remarkable progress in mathematical reasoning, but still continue to struggle with high-precision tasks like numerical computation and formal symbolic manipulation. Integrating external tools has emerged as a promising approach to bridge this gap. Despite recent advances, existing methods struggle with three key challenges: constructing tool-integrated reasoning data, performing fine-grained optimization, and enhancing inference. To overcome these limitations, we propose THOR (Tool-Integrated Hierarchical Optimization via RL). First, we introduce TIRGen, a multi-agent actor-critic-based pipeline for constructing high-quality datasets of tool-integrated reasoning paths, aligning with the policy and generalizing well across diverse models. Second, to perform fine-grained hierarchical optimization, we introduce an RL strategy that jointly optimizes for both trajectory-level problem solving and step-level code generation. This is motivated by our key insight that the success of an intermediate tool call is a strong predictor of the final answer's correctness. Finally, THOR incorporates a self-correction mechanism that leverages immediate tool feedback to dynamically revise erroneous reasoning paths during inference. Our approach demonstrates strong generalization across diverse models, performing effectively in both reasoning and non-reasoning models. It further achieves state-of-the-art performance for models of a similar scale on multiple mathematical benchmarks, while also delivering consistent improvements on code benchmarks. Our code will be publicly available at https://github.com/JingMog/THOR.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces THOR, a new way to help AI models solve math problems better. The main idea is to let the AI think step by step and use outside “tools” (like a calculator or a small Python program) whenever it needs precise calculations. THOR also trains the AI to learn from its mistakes and fix them during problem solving.
What Questions Does the Paper Try to Answer?
The authors focus on three big questions:
- How can we build good training data that shows an AI when and how to use tools (like code) while thinking through math problems?
- How can we train the AI not just to get the final answer right, but also to improve each small step (especially the parts where it writes code)?
- How can we make the AI fix its own mistakes while it’s solving a problem, using immediate feedback from tools?
Methods and Approach
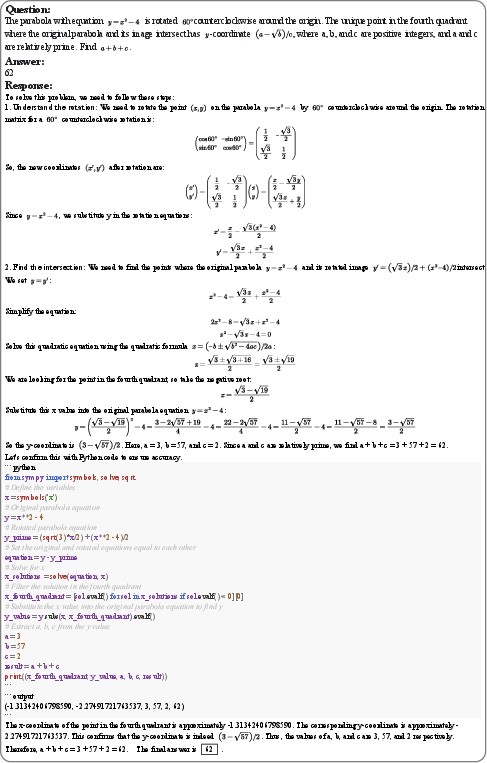
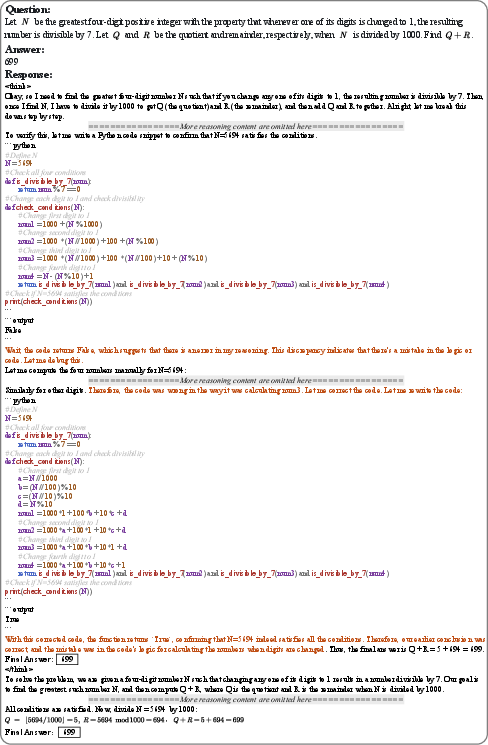
Think of the AI as a student who solves problems with a notebook (its “thoughts”) and a calculator (the “tool”). THOR has three main parts:
1) TIRGen: Building Better “Tool-Integrated” Training Data
- Two helpers work together:
- The “Actor”: writes the reasoning steps in plain language (like a student explaining their thinking).
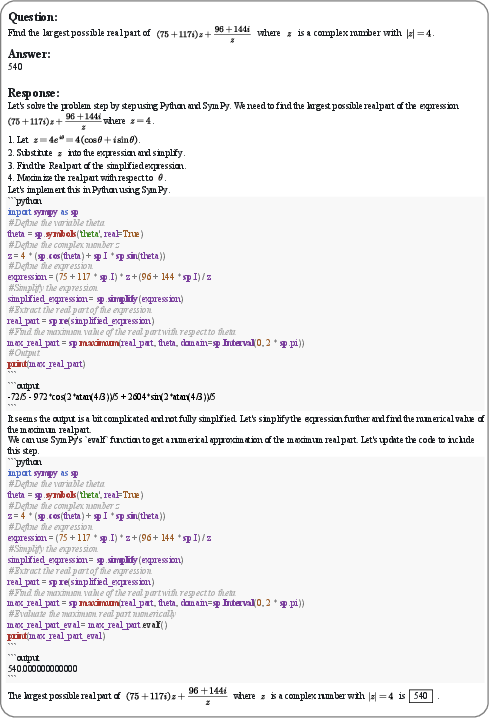
- The “Critic”: spots parts that are easier and more reliable to do with code (like calculations or solving equations), turns those parts into short Python code, runs the code, and adds the results back into the explanation.
- This creates training examples where the AI naturally switches between thinking and tool use, matching the AI’s own style and making the data more useful for training.
- The data is cleaned to remove broken code, enforce a clear format, and keep a good balance of difficulty.
2) Hierarchical RL: Training at Two Levels
RL (Reinforcement Learning) is like giving points for good behavior. THOR uses RL in two layers:
- Trajectory-level (the whole solution): reward the model when it gets the final answer right. This improves overall problem solving.
- Step-level (specific moments): when a code step fails (say the Python snippet errors out), the model gets targeted training to write better code for that exact step. This sharpens its coding skills where it matters.
- Key insight: if intermediate tool calls succeed (the code runs and returns the right thing), the final answer is much more likely to be correct. So training focuses on making these tool calls work well.
3) Self-Correction During Inference (While Solving)
- As the AI solves a problem, it follows a loop: think → act (call a tool) → observe (see the result).
- If a tool call fails (like the code errors), THOR doesn’t just keep going. It “backtracks” to the recent reasoning line, rewrites the end of that line, tries a new tool call, and keeps going. This is like erasing the last few lines and trying a different approach immediately.
- It can repeat this fix-and-retry a few times, but only for the part that went wrong, keeping the extra cost small.
Main Findings and Why They Matter
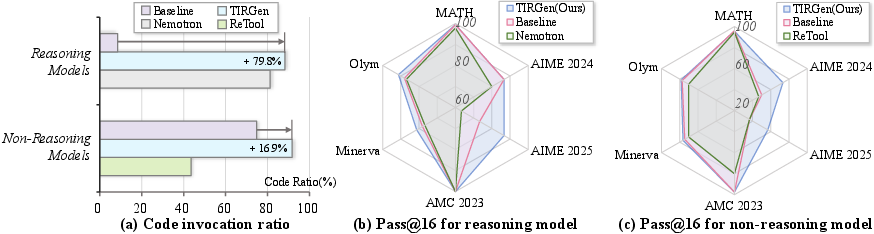
- THOR improves math performance across many benchmarks (like MATH500, AIME 2024/2025, AMC, Minerva Math, Olympiad Bench). It sets new records among models of similar size and works well on both “reasoning” models (that think in longer steps) and standard models.
- THOR also boosts code generation scores (on HumanEval+, MBPP+, LiveCodeBench), even though it wasn’t trained specifically for coding tasks. This shows the method generalizes beyond math.
- The “self-rewarded” approach at test time—generating several solution candidates and picking the one with the highest tool success rate—improves results further without needing an extra grading model.
- The authors found that successful mid-steps (tool calls that run and return good results) are strong indicators the final answer will be correct. This validates their strategy to train on both the full solution and the tricky code steps.
Why it matters:
- Many AI models struggle with exact calculations and formal steps; they’re good at language but can “guess” incorrectly. Using tools ensures precision.
- Training the AI to fix mistakes on the spot makes it more reliable and reduces wasted computation.
Implications and Impact
THOR shows a practical path to smarter problem-solving AIs:
- It teaches them not just to “think,” but to use tools at the right times for accurate results.
- It gives them a way to learn from immediate feedback and correct themselves mid-solution.
- It reduces the need for giant datasets or huge models by building policy-aligned training data and fine-tuning where it matters most.
- This approach could extend to science, engineering, and other fields where precise steps and calculations are essential, helping AI become both more trustworthy and more efficient.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of what remains missing, uncertain, or unexplored in the paper, phrased to be directly actionable for future research.
- TIRGen critic design and training: The paper does not specify how
JudgeCodeSolvable,ExtractLogic, andConvertToCodeare implemented, trained, or evaluated. What architectures, prompts, and criteria does the critic use, and how robust is it to false positives/negatives in identifying code-solvable steps? - Semantic equivalence guarantees: There is no formal or empirical validation that the critic’s code faithfully preserves the actor’s intended semantics at each step. How often do converted snippets change the reasoning logic or silently introduce errors?
- Step-level reward fidelity: Step-level rewards are based on execution success/failure, but execution success does not guarantee semantic correctness. Can more informative rewards (e.g., property-based tests, unit tests, symbolic checks, invariants) better align step-level optimization with final correctness?
- Failure taxonomy and targeted fixes: The method does not analyze or differentiate failure modes (syntax error, runtime error, numerical instability, logical error). Which error types are most prevalent, and which benefit most from step-level RL and self-correction?
- Hyperparameter sensitivity: Critical choices such as
L_step,L_suf,N_corr, group sizeG, clipping ranges, and the weight α for the NLL term lack sensitivity analyses. How do these settings trade off performance, stability, and cost? - Credit assignment across steps: The hierarchical RL optimizes failed steps in isolation, but does not address how local fixes interact with downstream steps. Can multi-step credit assignment or multi-step local rollouts improve end-to-end solution quality?
- Long-horizon planning: Step-level optimization uses a single think–act–observe loop per sample. How does the method scale to long trajectories requiring coordinated multi-step code planning or multi-tool pipelines?
- Tool overuse bias: The TIRGen filter removes instances solvable by pure CoT and requires code features (libraries/control flow), which may bias models toward calling tools even when unnecessary. Does this harm performance on problems best solved without code?
- Tool selection calibration: The paper does not assess whether the model accurately decides when to call tools versus reason in natural language. Can we measure and improve “tool necessity prediction” and false positive/negative tool calls?
- Environment/sandbox robustness: Execution failures may be due to environment issues (timeouts, package versions, resource limits). How sensitive are results to sandbox parameters, and can environment-aware training prevent penalizing the model for infrastructure noise?
- Security and safety of code execution: No discussion of sandbox hardening, malicious code prevention, or side-channel risks. What security constraints and auditing are necessary to safely scale tool-integrated training/inference?
- Generalization across tools and languages: The approach is evaluated with a Python interpreter (and libraries like SymPy/NumPy). How well does it transfer to other tools (e.g., CAS beyond SymPy, SMT solvers, theorem provers, spreadsheets, external APIs) or other programming languages?
- Formal reasoning and proof generation: The paper emphasizes numerical/symbolic computation but does not evaluate on formal proofs (e.g., Lean/Isabelle). Can the framework extend to proof assistants and formal verification tasks?
- Theoretical grounding of the “intermediate tool success → final correctness” claim: This key insight is empirically noted (Appendix) but lacks theoretical analysis or robustness checks across domains. Under what conditions does this correlation hold or fail?
- ORM-free selection via pass rate: Best-of-N selection uses code execution pass rate as a proxy reward. What is the quantitative correlation between pass rate and final-answer correctness across tasks, and does it hold for problems where code checks are brittle or partial?
- Dataset provenance and contamination: The source
D_qfor TIRGen is unspecified. Are there overlaps with evaluation benchmarks? A data contamination audit and transparent dataset documentation are needed for fair comparisons. - Scale and composition of TIRGen data: The paper omits the size, domain distribution, and difficulty spectrum of the generated dataset. How do dataset size, code-call count distribution, and topic coverage affect learning and generalization?
- Comparative data controls: Ablations compare TIRGen against other TIR datasets without controlling for dataset size, difficulty, or stylistic differences. Can matched-size, matched-difficulty comparisons isolate the contribution of data style versus quantity?
- RL stability and compute efficiency: While GRPO and NLL regularization are used, the paper does not report training stability, variance, sample efficiency, or compute cost. How does THOR compare to alternative RL algorithms (e.g., VAPO, PPO variants) in stability/efficiency on long-CoT regimes?
- Masking observations in loss: External observations
o^tare masked during loss computation; the implications for learning dynamics are not analyzed. Does masking hinder credit assignment or encourage spurious formatting dependence? - Self-correction cost–benefit analysis: The claim of “minimal cost” for suffix regeneration is not quantified. What are the latency and compute overheads per correction attempt, and how do they scale with
N_corrand context length? - Interaction with test-time scaling: The interplay between self-correction and Best-of-N sampling is not explored. Can structured search (e.g., tree/beam with tool-aware scoring) outperform simple BoN with similar or lower cost?
- Tool call budget optimization: There is no explicit mechanism to manage or optimize the number of tool calls under latency or cost constraints. Can reward shaping or budgeting produce better accuracy–cost trade-offs?
- Robustness to nondeterminism: The framework does not address nondeterministic code execution (random seeds, floating-point variability, external API variability). How does nondeterminism affect reward signals and reproducibility?
- Generalization beyond math and coding: Claims of broad generalization are limited to math and code benchmarks. How does THOR perform on other reasoning domains (e.g., physics word problems, data analysis, scientific QA, planning with tools)?
- Grading reliability: Mathematical answer checking relies on Qwen3-32B to compare predictions with ground truth, which may misgrade due to parsing or symbolic simplification errors. Can exact-checking pipelines (symbolic normalization, numeric tolerances, canonicalization) reduce grading noise?
- Statistical significance and variance: Reported improvements lack confidence intervals, significance tests, and per-seed variance. Are gains robust across seeds, sampling temperatures, and random initializations?
- Catastrophic forgetting of pure CoT: Emphasizing tool-integrated training may degrade pure language reasoning. Does THOR maintain or improve performance on tasks requiring minimal or no tool usage?
- Multi-agent pipeline ablations: The paper does not paper how critic quality affects TIRGen outputs and downstream performance. What happens when the critic is weaker/stronger, or replaced by a single-model pipeline?
- Multi-modal math (e.g., geometry diagrams): Many competition problems involve diagrams or figures; the current pipeline is text/code-only. Can tool-integrated reasoning incorporate vision and geometric toolkits?
- Interpretability and trace verification: There is no mechanism to verify that intermediate tool outputs are correctly used in subsequent steps. Can explicit trace-checking or constraint verification detect and correct misuse of tool outputs?
- Ethical and fairness considerations: The work does not assess whether tool integration introduces biases (e.g., favoring problems compatible with certain libraries) or disadvantages models/tools with different resource constraints.
- Release artifacts and reproducibility details: Code/data release is promised but not yet available; key training details (hyperparameters, data sizes, compute) are deferred to appendices. Clear, executable recipes and environment snapshots are needed for full reproducibility.
Collections
Sign up for free to add this paper to one or more collections.