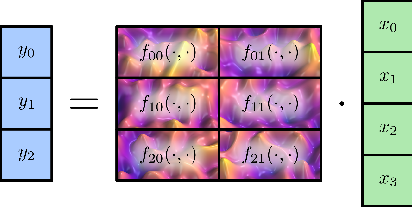Lookup multivariate Kolmogorov-Arnold Networks (2509.07103v1)

Abstract: High-dimensional linear mappings, or linear layers, dominate both the parameter count and the computational cost of most modern deep-learning models. We introduce a general drop-in replacement, lookup multivariate Kolmogorov-Arnold Networks (lmKANs), which deliver a substantially better trade-off between capacity and inference cost. Our construction expresses a general high-dimensional mapping through trainable low-dimensional multivariate functions. These functions can carry dozens or hundreds of trainable parameters each, and yet it takes only a few multiplications to compute them because they are implemented as spline lookup tables. Empirically, lmKANs reduce inference FLOPs by up to 6.0x while matching the flexibility of MLPs in general high-dimensional function approximation. In another feedforward fully connected benchmark, on the tabular-like dataset of randomly displaced methane configurations, lmKANs enable more than 10x higher H100 throughput at equal accuracy. Within frameworks of Convolutional Neural Networks, lmKAN-based CNNs cut inference FLOPs at matched accuracy by 1.6-2.1x and by 1.7x on the CIFAR-10 and ImageNet-1k datasets, respectively. Our code, including dedicated CUDA kernels, is available online at https://github.com/schwallergroup/lmkan.

• The paper introduces lmKANs as an efficient drop-in replacement for high-dimensional linear mappings using multivariate spline lookup tables.
• It leverages the Kolmogorov-Arnold theorem and custom CUDA kernels to achieve up to 88× better per-parameter inference efficiency than traditional linear layers.
• Empirical results show significant reductions in FLOPs and inference cost across function approximation, tabular regression, and CNN benchmarks.

Lookup Multivariate Kolmogorov-Arnold Networks: Architecture, Efficiency, and Empirical Analysis

Introduction and Motivation

The paper introduces Lookup Multivariate Kolmogorov-Arnold Networks (lmKANs) as a general-purpose, drop-in replacement for high-dimensional linear mappings in deep learning architectures. The motivation stems from the observation that linear layers dominate both parameter count and computational cost in modern models, with their $\mathcal{O}(N^2)$ scaling. lmKANs leverage trainable low-dimensional multivariate functions, implemented as spline lookup tables, to achieve a substantially improved trade-off between model capacity and inference cost. The approach is grounded in the Kolmogorov-Arnold Representation Theorem (KART), but extends the classical univariate KAN paradigm to multivariate settings, enabling richer parametrization and more efficient computation.

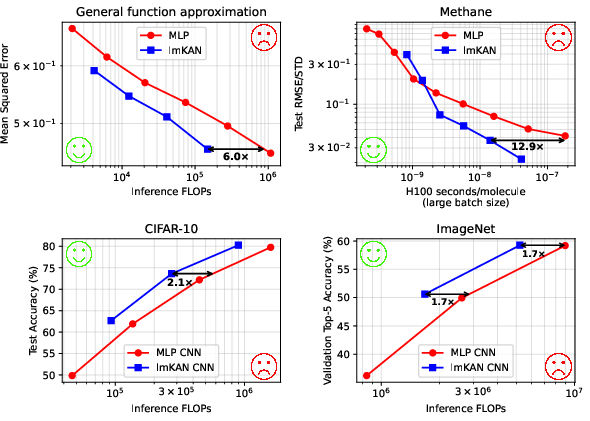
Figure 1: Performance summary of lmKANs across general function approximation, tabular regression, and CNN benchmarks, highlighting Pareto-optimality in the FLOPs-accuracy plane.

Architecture and Parametrization

Multivariate Spline Lookup Layers

lmKAN layers replace standard linear mappings with collections of trainable $d$-dimensional functions, each parameterized by second-order B-splines on a static percentile grid. For the 2D case, each function $f(x_1, x_2)$ is represented as:

$$f(x_1, x_2) = \sum_{i_1, i_2} p_{i_1 i_2} B_{i_1 i_2}(x_1, x_2)$$

where $B_{i_1 i_2}(x_1, x_2)$ are tensor products of 1D B-splines, and $p_{i_1 i_2}$ are trainable coefficients. The grid is constructed using a fast sigmoid-like function $\sigma(x)$, approximating the standard Gaussian CDF, to ensure efficient $\mathcal{O}(1)$ lookup and balanced parameter utilization.

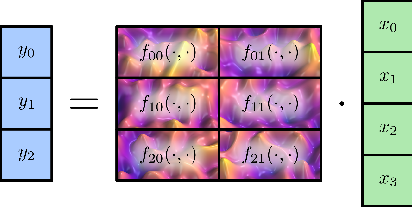
Figure 2: Schematic of a 2D lmKAN layer with 4 inputs and 3 outputs, each output computed as a sum of two trainable bivariate functions.

Figure 3: (a) Construction of the sigma grid; (b) example piecewise linear function; (c) second-order B-spline; (d) two-dimensional B-spline basis.

Computational Complexity

The dominant cost of a 2D lmKAN layer is $2N_{\text{in}}N_{\text{out}}$ fused multiply-adds, exactly $2\times$ that of a linear layer of the same shape. The number of trainable parameters per function scales as $(G+1)^2$, where $G$ is the number of grid intervals, allowing hundreds of times more parameters than a linear layer without increasing inference FLOPs. Custom CUDA kernels are implemented for efficient GPU inference, achieving up to $88\times$ better inference time per parameter compared to linear layers on H100 GPUs.

Regularization and Training Stability

Generalization Pitfalls

Direct fitting of high-resolution splined functions can lead to poor generalization, as only a small subset of parameters receive gradient updates, and non-active coefficients remain random or are zeroed by L2 regularization.

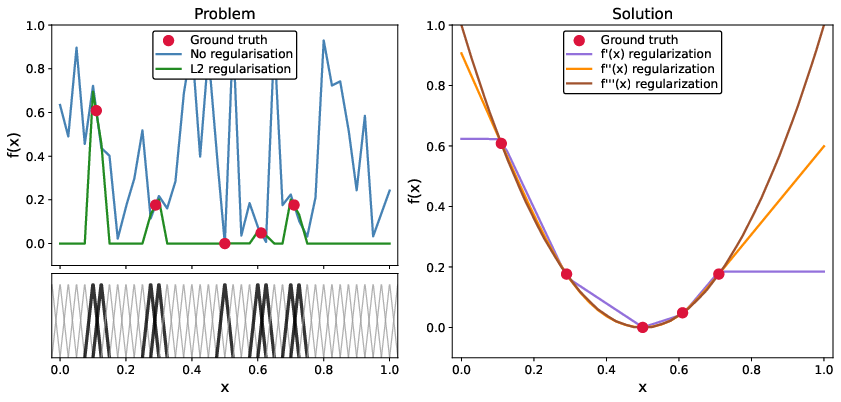
Figure 4: Illustration of generalization pitfalls in high-resolution spline fitting, showing poor extrapolation outside training points.

Hessian Regularization

To address this, the paper introduces off-diagonal regularization based on the squared Frobenius norm of the Hessian, which penalizes curvature and enforces smoothness. The regularization coefficient $\lambda$ allows interpolation between unconstrained lmKAN and linear MLP behavior. A multi-staged fitting procedure is employed, starting with strong regularization and gradually decaying $\lambda$ to stabilize training.

Empirical Evaluation

General Function Approximation

lmKANs are benchmarked against MLPs in the task of distilling high-dimensional functions from large random teacher networks. Both architectures use two hidden layers and batch normalization. lmKANs consistently achieve up to $6\times$ fewer inference FLOPs at matched accuracy, and $1.8\times$ faster H100 wall-clock time for large hidden dimensions.

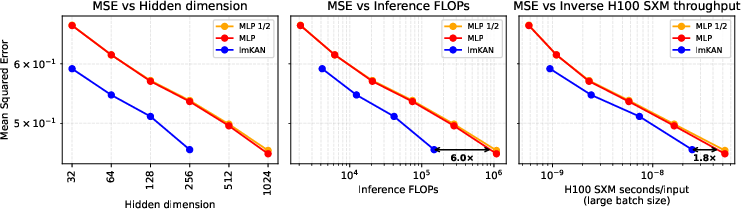
Figure 5: lmKAN vs MLP for general function approximation, showing superior FLOPs-accuracy trade-off for lmKANs.

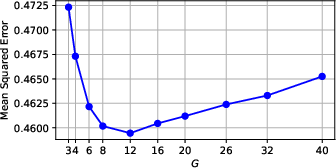
Figure 6: Final MSE vs grid resolution $G$ for hidden_dim=256 lmKAN, revealing an optimal $G$ due to convergence difficulties at high resolutions.

Tabular Regression: Methane Configurations

On the dataset of randomly displaced methane configurations, lmKANs outperform MLPs across multiple invariant representations. For the "Distances" modality, lmKANs deliver more than $10\times$ higher H100 throughput at equal accuracy. The regularized variant further improves generalization, especially in symmetry-preserving representations.

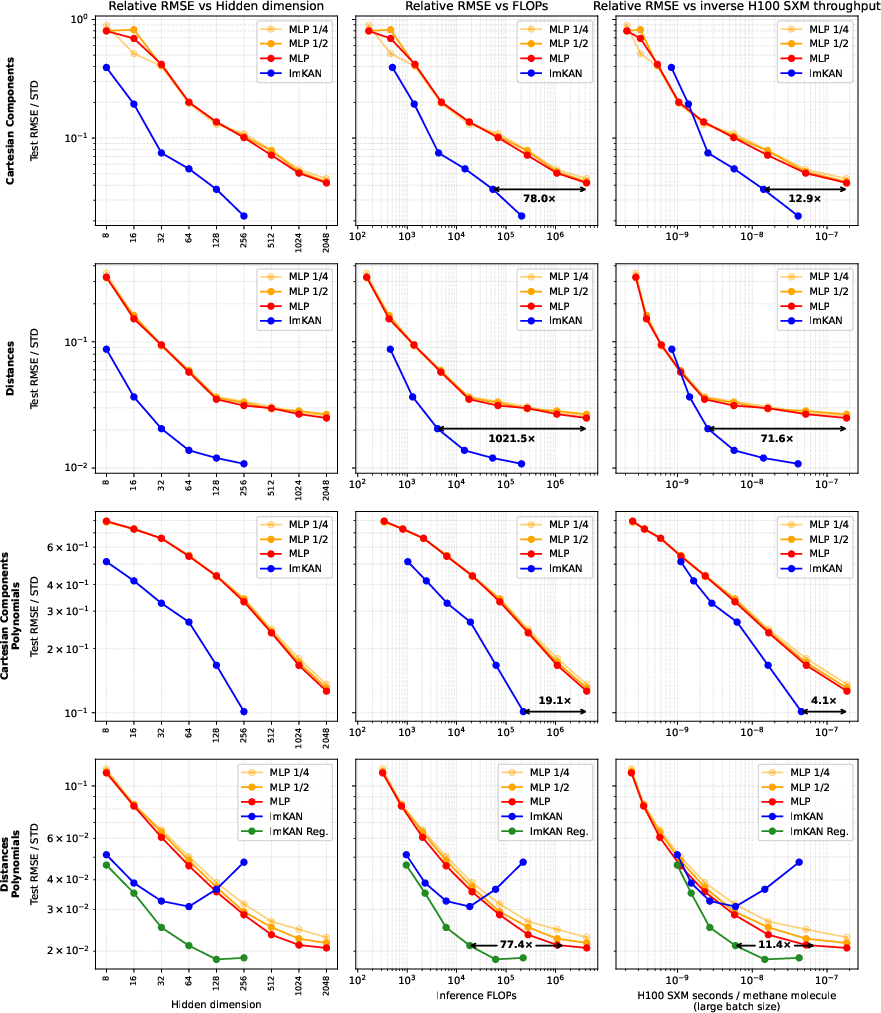
Figure 7: lmKAN vs MLP on methane regression, with Hessian regularization mitigating overfitting and achieving Pareto-optimality.

Convolutional Neural Networks

lmKAN-based CNNs are evaluated on CIFAR-10 and ImageNet. Replacing standard convolutions with lmKAN-based ones reduces inference FLOPs by $1.6$–$2.1\times$ on CIFAR-10 and $1.7\times$ on ImageNet, with matched or superior accuracy.

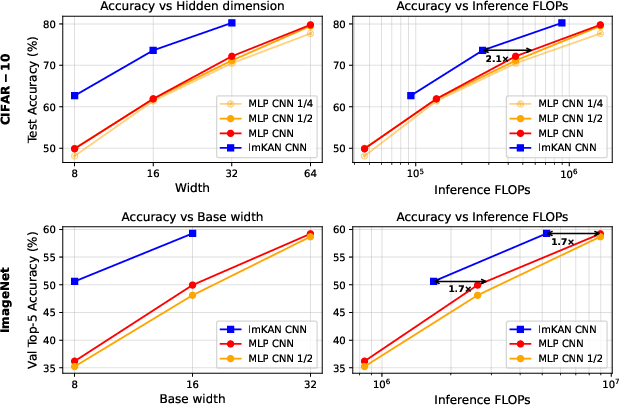
Figure 8: Comparison of MLP-based and lmKAN-based CNNs on CIFAR-10 and ImageNet, demonstrating FLOPs reduction at matched accuracy.

Comparison with FastKAN

lmKANs are compared to FastKANs in fully-connected settings. lmKANs exhibit superior training stability and accuracy, especially at high parameter budgets, due to the coarser grid and multivariate parametrization, which restricts expressivity to lower-frequency function classes.

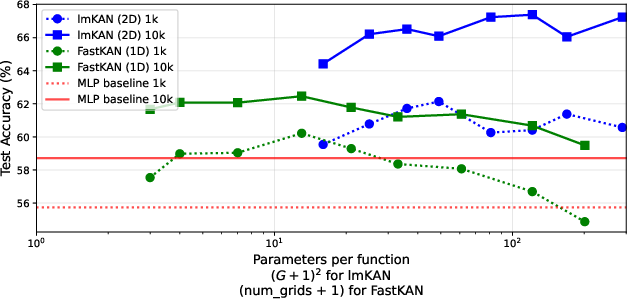
Figure 9: lmKAN vs FastKAN on CIFAR-10, showing lmKAN's robustness to grid resolution and superior accuracy.

Implementation and Scaling Considerations

CUDA Kernel Performance

lmKAN CUDA kernels are benchmarked on H100 SXM GPUs. For large dimensions, the kernels are $8\times$ slower than dense linear layers, but the per-parameter efficiency is $27.5\times$ better at $G=20$, and $88.5\times$ better at $G=40$ with smaller tiles. For small feature dimensions, the slowdown is only $2.5\times$.

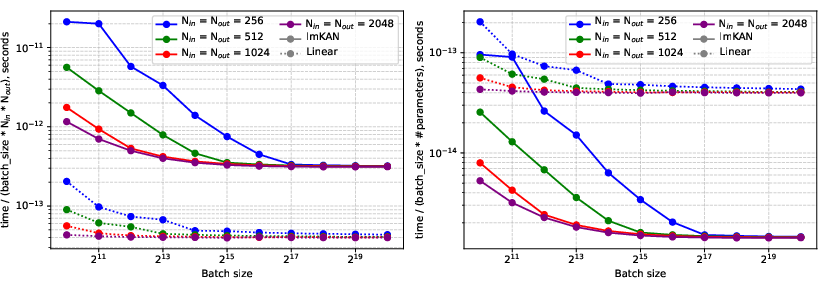
Figure 10: CUDA kernel performance for large dimensions, showing time normalized by shape and by parameter count.

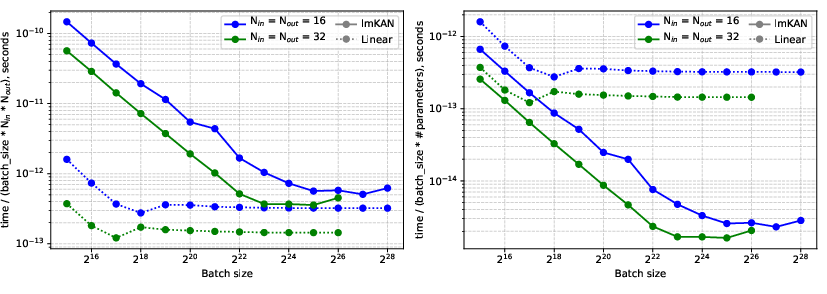
Figure 11: CUDA kernel performance for small dimensions, with improved relative efficiency.

Figure 12: Inference efficiency of lmKAN layers as a function of grid intervals $G$, confirming independence of throughput from $G$.

Training Pipeline

A multi-staged fitting procedure is used, starting with pure MLP mode, gradually increasing lmKAN contribution, and decaying Hessian regularization. Preconditioning schemes (ReLU-first vs ReLU-last) are compared, with ReLU-first offering absorption into lmKAN layers and lower inference cost.

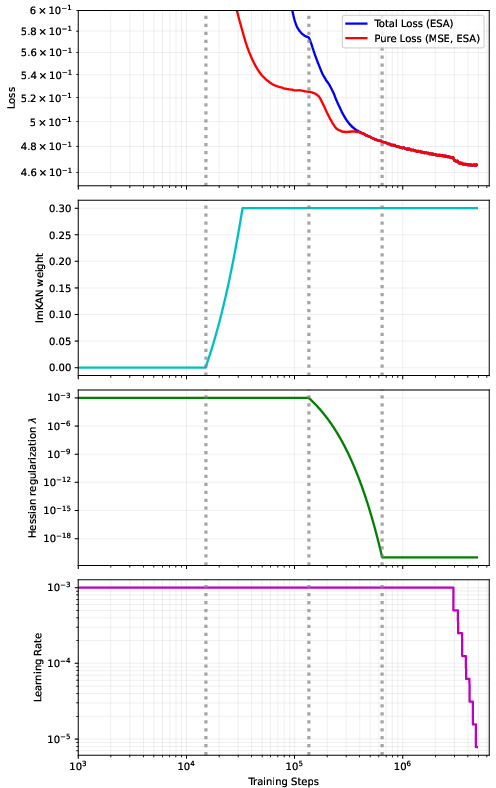
Figure 13: Multi-staged fitting procedure, showing loss dynamics and regularization decay.

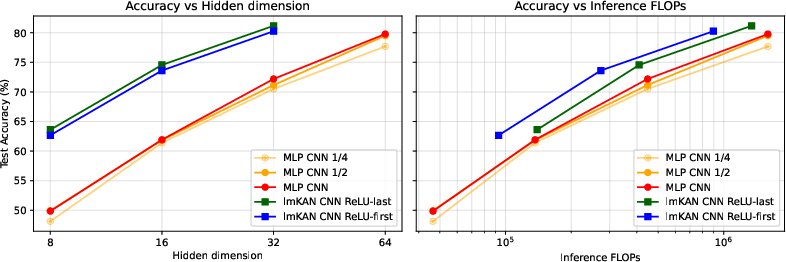
Figure 14: Preconditioning scheme comparison on CIFAR-10.

Figure 15: Preconditioning scheme comparison in general function approximation.

Limitations

lmKANs are harder to converge at excessively high grid resolutions $G$, and large $G$ increases memory requirements. Current CUDA kernels are implemented only for float32; support for lower-precision types (e.g., bfloat16) is pending. Latency, while not dependent on $G$ in throughput, can be affected in practice.

Implications and Future Directions

lmKANs provide a principled and efficient alternative to high-dimensional linear mappings in deep learning, with strong empirical evidence for Pareto-optimality in the FLOPs-accuracy plane across diverse tasks. The approach is compatible with existing architectures and can be extended to higher-dimensional splines, though with increased computational cost. The use of multivariate spline lookup tables opens avenues for further research in conditional computation, hardware co-design, and efficient parametrization of complex function classes. Future work may focus on improved optimization schemes for high-resolution grids, support for mixed-precision inference, and integration with domain-specific architectures.

Conclusion

Lookup multivariate Kolmogorov-Arnold Networks (lmKANs) represent a significant advancement in the efficient parametrization and computation of high-dimensional mappings in deep learning. By leveraging multivariate spline lookup tables and custom GPU kernels, lmKANs achieve substantial reductions in inference FLOPs and wall-clock time while maintaining or improving accuracy across general function approximation, tabular regression, and convolutional settings. Theoretical and empirical analyses support the superiority of multivariate parametrization over univariate alternatives, and the proposed regularization and training schemes ensure robust generalization. lmKANs are well-positioned for broad adoption as a scalable, efficient replacement for linear layers in modern neural architectures.