Saturation-Driven Dataset Generation for LLM Mathematical Reasoning in the TPTP Ecosystem (2509.06809v1)

Abstract: The scarcity of high-quality, logically sound data is a critical bottleneck for advancing the mathematical reasoning of LLMs. Our work confronts this challenge by turning decades of automated theorem proving research into a scalable data engine. Rather than relying on error-prone LLMs or complex proof-assistant syntax like Lean and Isabelle, our framework leverages E-prover's saturation capabilities on the vast TPTP axiom library to derive a massive, guaranteed-valid corpus of theorems. Our pipeline is principled and simple: saturate axioms, filter for "interesting" theorems, and generate tasks. With no LLMs in the loop, we eliminate factual errors by construction. This purely symbolic data is then transformed into three difficulty-controlled challenges: entailment verification, premise selection, and proof reconstruction. Our zero-shot experiments on frontier models reveal a clear weakness: performance collapses on tasks requiring deep, structural reasoning. Our framework provides both the diagnostic tool to measure this gap and a scalable source of symbolic training data to address it. We make the code and data publicly available. https://github.com/sileod/reasoning_core https://hf.co/datasets/reasoning-core/rc1

• The paper presents a saturation-driven pipeline that exhaustively generates proof graphs from the TPTP axiom library using E-prover's capabilities.
• It combines heuristic scoring with AGInTRater and validation via Vampire to curate a reliable corpus of non-trivial, mathematically relevant theorems.
• Experimental evaluations reveal that even advanced LLM models struggle with multi-step, structural proof reconstructions, highlighting a key challenge in symbolic reasoning.

Saturation-Driven Dataset Generation for LLM Mathematical Reasoning in the TPTP Ecosystem

Motivation and Context

The paper addresses a central bottleneck in the development of LLMs for mathematical reasoning: the lack of large-scale, logically sound training data. Unlike domains with abundant web-scale corpora, formal mathematical proofs are scarce, expensive to produce, and require expert annotation. Existing synthetic data generation approaches often rely on LLMs themselves or on complex proof assistant syntax, introducing risks of factual errors and limiting diversity. The proposed framework leverages the mature automated theorem proving (ATP) ecosystem, specifically E-prover's saturation capabilities on the TPTP axiom library, to generate a massive, guaranteed-valid corpus of theorems. This approach is fully symbolic, eliminating LLM-induced errors and enabling scalable, reproducible dataset generation.

Framework Architecture

The pipeline consists of three deterministic stages:

1. Exhaustive Generation via Saturation: E-prover is configured in saturation mode to derive the deductive closure of a selected TPTP axiom set, outputting a full proof graph (DAG) of all logical consequences up to a computational timeout.
2. Curation with Interest Metrics: AGInTRater heuristically scores each derived clause for "interestingness" based on complexity, surprisingness, and usefulness, allowing the selection of non-trivial, mathematically relevant theorems.
3. Task Formulation and Validation: The curated graph is modeled in NetworkX, and Vampire is used as a ground-truth oracle to validate all entailment queries, ensuring logical soundness.

This pipeline is fully automated, model-agnostic, and capable of producing unlimited tasks with controllable difficulty.

Task Suite: Deconstructing Theorem Proving

The framework decomposes mathematical reasoning into three complementary tasks:

• Conjecture Entailment Verification: Given a set of context axioms and a perturbed set of premises, the model must decide if a specific theorem is entailed. Difficulty is modulated by proof depth and premise perturbations.
• Minimal Premise Selection: From a noisy pool of premises (including distractors), the model must identify the minimal sufficient subset required to prove a theorem. Difficulty is controlled by the number of distractors and proof depth.
• Proof Graph Reconstruction: The model receives a shuffled list of clauses from a binary proof subgraph and must reconstruct the parent-child relationships, testing global structural reasoning.

Each task is parameterized for fine-grained control over logical complexity and noise.

Experimental Evaluation

Zero-shot experiments were conducted on three GPT-5 model variants (nano, mini, full) across five TPTP domains (Algebra, Fields, Geometry, Set Theory, Topology), with 3,000 benchmark problems spanning four difficulty levels.

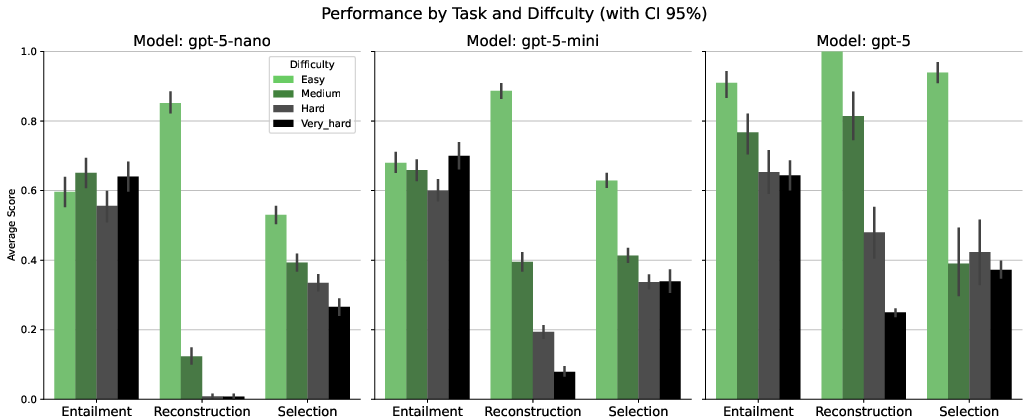
Figure 1: Performance comparison of three model scales on the three reasoning tasks, aggregated across all domains. Performance degrades with increasing difficulty, and proof graph reconstruction is significantly more challenging, especially for smaller models.

Key findings:

• Performance Degradation with Complexity: All models show a marked decline in accuracy as proof depth and distractor count increase. The effect is most pronounced for proof graph reconstruction, where smaller models fail almost completely.
• Model Scale Effects: Larger models outperform smaller ones, particularly on high-difficulty tasks, but even the largest model struggles with global structural reasoning.
• Structural Reasoning Bottleneck: The inability of current LLMs to reconstruct multi-step, hierarchical proofs highlights a fundamental architectural limitation not resolved by scaling alone.

Qualitative Analysis of Proof Graph Reconstruction

The paper provides detailed visualizations of model outputs for the proof graph reconstruction task, overlaying predicted dependencies on the ground truth.

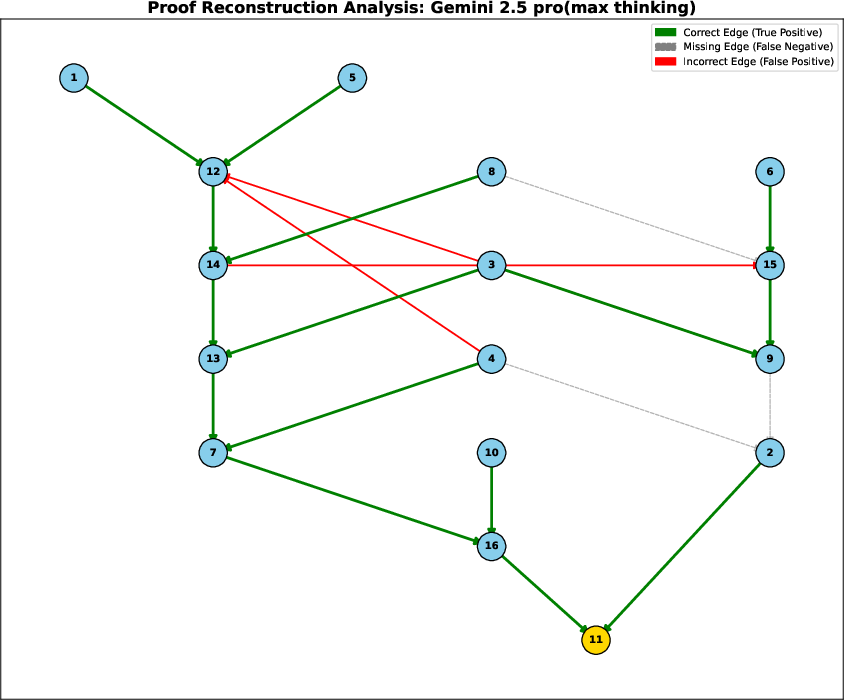
Figure 2: Proof graph reconstruction analysis for Gemini 2.5 pro. Most dependencies are correct, but several hallucinated and missing edges remain.

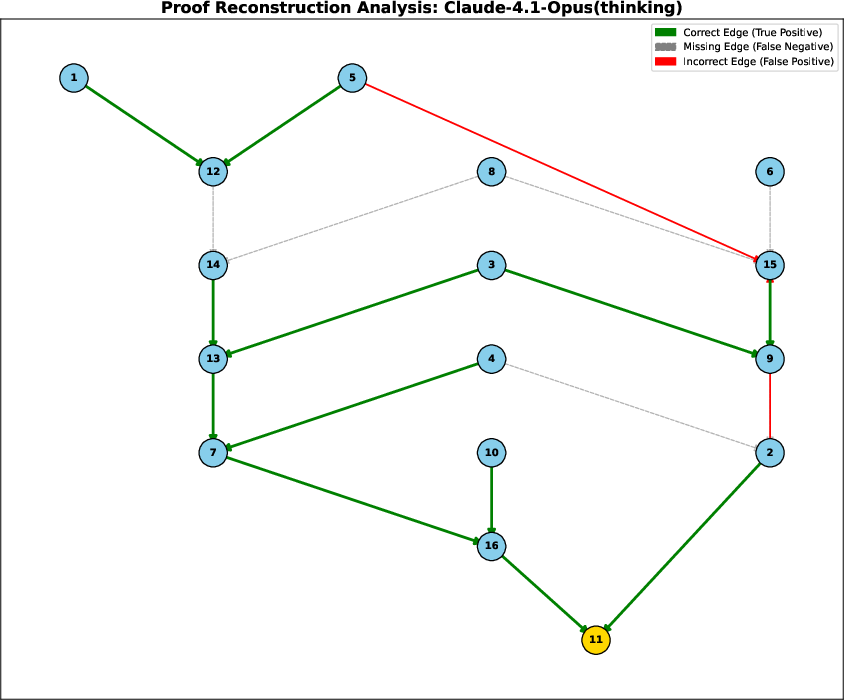
Figure 3: Proof graph reconstruction analysis for Claude-4.1-Opus. Main path is identified, but multiple incorrect and missing dependencies are present.

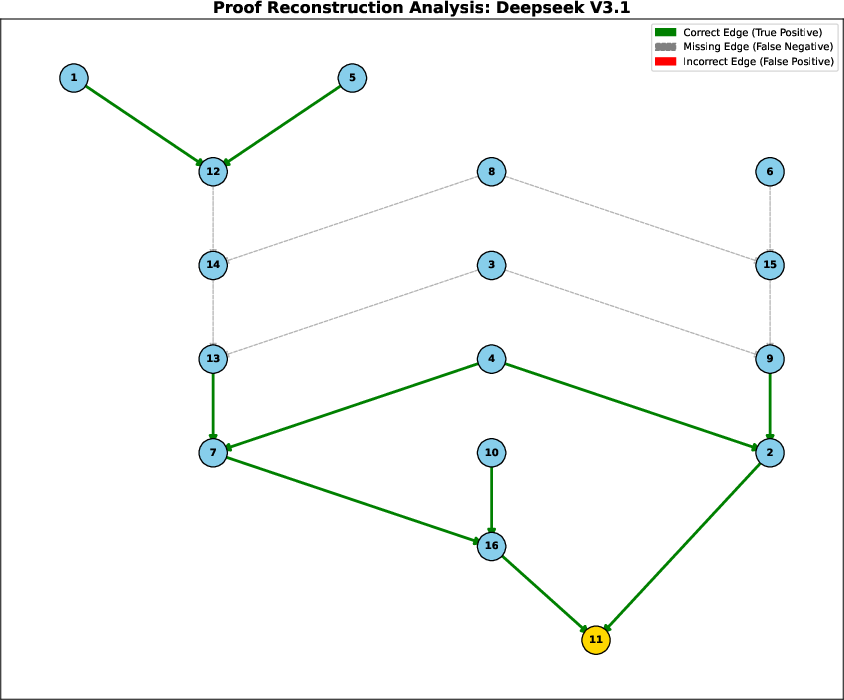
Figure 4: Proof graph reconstruction analysis for Deepseek V3.1. High precision but low recall; many correct edges but incomplete graph.

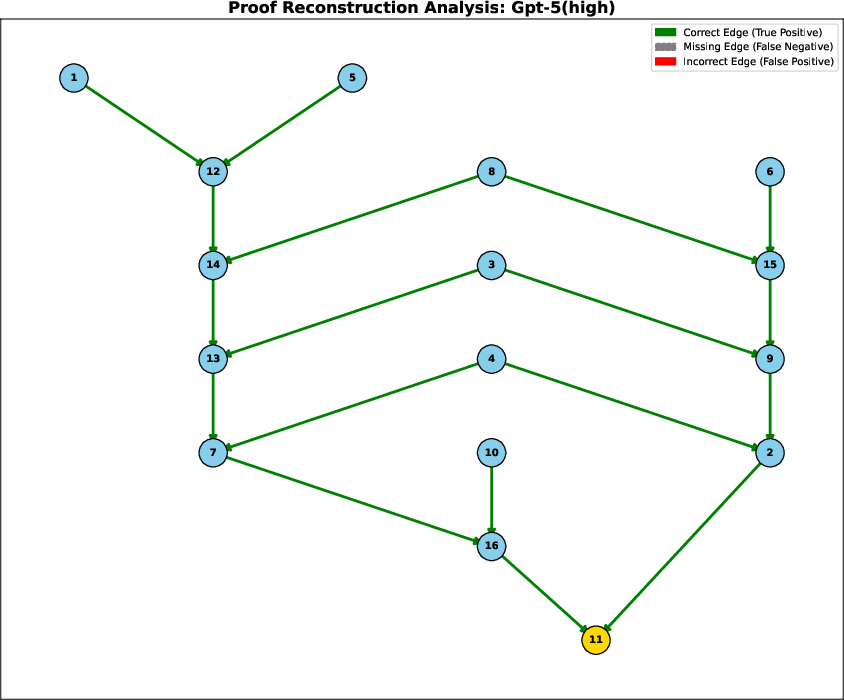
Figure 5: Proof graph reconstruction analysis for Gpt-5(high). Perfect reconstruction; all dependencies are correct and complete.

These results demonstrate that only the largest, most capable models can achieve perfect reconstruction, and even then, only on tractable proof depths. Other models either hallucinate dependencies or fail to recover the full structure, indicating a persistent gap in deep symbolic reasoning.

Implementation Considerations

• Computational Requirements: Saturation with E-prover is bounded by timeouts due to combinatorial explosion. AGInTRater and Vampire are efficient for curation and validation, respectively.
• Scalability: The pipeline is designed for unlimited data generation, with difficulty and domain coverage controlled by input parameters.
• Deployment: The framework is open-source and can be integrated into LLM training pipelines for both benchmarking and curriculum learning.
• Limitations: The current implementation operates exclusively in CNF, abstracting away natural language complexity to isolate pure reasoning. Extension to full FOL is planned.

Implications and Future Directions

The framework provides a robust diagnostic tool for probing LLM reasoning depth and a scalable source of symbolic training data. The results suggest that current LLMs lack robust multi-step, structural deduction capabilities, and that scaling alone is insufficient. Future work will focus on:

• Fine-tuning LLMs on symbolic datasets to test transferability to natural language reasoning.
• Iterative saturation to generate even more complex deductive chains.
• Extension to full first-order logic for increased expressiveness.

The open-source release of code and data is intended to catalyze further research into neuro-symbolic integration and the development of AI systems with rigorous mathematical reasoning.

Conclusion

The paper presents a principled, scalable framework for generating logically sound mathematical reasoning tasks, leveraging symbolic ATP tools to overcome the data bottleneck in LLM training. Empirical results reveal persistent weaknesses in multi-step and structural reasoning, motivating the need for targeted training and architectural innovation. The framework is positioned as both a benchmark and a data engine for advancing the state of mathematical reasoning in AI.