SynLogic: Synthesizing Verifiable Reasoning Data at Scale for Learning Logical Reasoning and Beyond (2505.19641v4)

Abstract: Recent advances such as OpenAI-o1 and DeepSeek R1 have demonstrated the potential of Reinforcement Learning (RL) to enhance reasoning abilities in LLMs. While open-source replication efforts have primarily focused on mathematical and coding domains, methods and resources for developing general reasoning capabilities remain underexplored. This gap is partly due to the challenge of collecting diverse and verifiable reasoning data suitable for RL. We hypothesize that logical reasoning is critical for developing general reasoning capabilities, as logic forms a fundamental building block of reasoning. In this work, we present SynLogic, a data synthesis framework and dataset that generates diverse logical reasoning data at scale, encompassing 35 diverse logical reasoning tasks. The SynLogic approach enables controlled synthesis of data with adjustable difficulty and quantity. Importantly, all examples can be verified by simple rules, making them ideally suited for RL with verifiable rewards. In our experiments, we validate the effectiveness of RL training on the SynLogic dataset based on 7B and 32B models. SynLogic leads to state-of-the-art logical reasoning performance among open-source datasets, surpassing DeepSeek-R1-Distill-Qwen-32B by 6 points on BBEH. Furthermore, mixing SynLogic data with mathematical and coding tasks improves the training efficiency of these domains and significantly enhances reasoning generalization. Notably, our mixed training model outperforms DeepSeek-R1-Zero-Qwen-32B across multiple benchmarks. These findings position SynLogic as a valuable resource for advancing the broader reasoning capabilities of LLMs. We open-source both the data synthesis pipeline and the SynLogic dataset at https://github.com/MiniMax-AI/SynLogic.

• The paper introduces SynLogic, a framework that synthesizes verifiable logical reasoning data at scale to boost LLM training via reinforcement learning.
• It presents a comprehensive data synthesis pipeline with task selection, parameter control, and prompt formalization to generate datasets for both 7B and 32B models.
• The study demonstrates that mixing logical, mathematical, and coding tasks improves training efficiency and generalization across multiple benchmarks.

SynLogic: Synthesizing Verifiable Reasoning Data at Scale for Learning Logical Reasoning and Beyond

This paper introduces #1, a data synthesis framework and dataset designed to generate diverse logical reasoning data at scale. The core hypothesis is that logical reasoning is fundamental for developing general reasoning capabilities in LLMs. The framework enables controlled synthesis of data with adjustable difficulty and quantity, with all examples being verifiable by simple rules, making them suitable for RL with verifiable rewards. Experiments validate the effectiveness of RL training on the #1 dataset using 7B and 32B models, achieving SOTA logical reasoning performance among open-source datasets. The paper further demonstrates that mixing #1 data with mathematical and coding tasks enhances training efficiency and generalization.

Data Synthesis Framework

The authors present a comprehensive data synthesis framework to generate diverse synthetic data at scale, encompassing 35 tasks. (Figure 1) illustrates the data synthesis pipeline, which includes task selection, parameter identification, logic instance generation, difficulty control, prompt formalization, and a verification suite.

(Figure 1)

Figure 1: The logic data synthesis framework, involving task selection, parameter identification, logic instance generation, difficulty control, prompt formalization, and verification suite.

The framework addresses the limitations of existing benchmarks that lack training support or are limited to a small number of tasks. The difficulty control mechanism allows for precise calibration of problem complexity through task-specific parameters, which enables the creation of progressively challenging training curricula. The authors synthesize two distinct versions of the dataset: #1-Hard for Qwen2.5-32B training and #1-Easy for Qwen2.5-7B training. The difficulty of the synthetic data is evaluated using avg@8 and pass@8 metrics, which confirms the appropriate difficulty levels for each model scale. (Figure 2) shows the performance of 7B and 32B models on the #1-Easy and #1-Hard datasets, respectively.

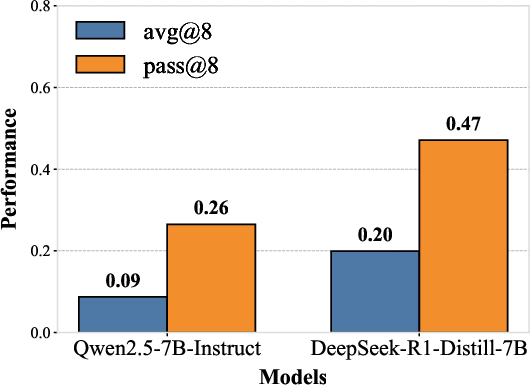
Figure 2: Model performance evaluation on #1-Easy and #1-Hard datasets using avg@8 and pass@8 metrics.

Reinforcement Learning Experiments

The paper validates the effectiveness of RL training on the #1 dataset using Qwen2.5-7B-Base and Qwen2.5-32B-Base models. The training employs a modified DAPO training prompt and a binary reward function that evaluates both format adherence and answer correctness.

The evaluation results demonstrate significant improvements across logical reasoning tasks, with the models achieving enhanced performance across multiple logical benchmarks. The 7B model achieves 48.1% on KOR-Bench, outperforming Qwen2.5-7B-Instruct by nearly 10 absolute percentage points. The 32B model surpasses Qwen2.5-32B-Instruct by 7 percentage points on KOR-Bench and exceeds R1-Distill-Qwen32B by 6 percentage points on the BBEH benchmark. Furthermore, the models exhibit strong generalization capabilities to mathematical domains. The authors observe that training on #1 data leads to stable increases in response length and the emergence of reflection behaviors. (Figure 3) illustrates the response length and reflection ratio across the training process for both the 7B and 32B models.

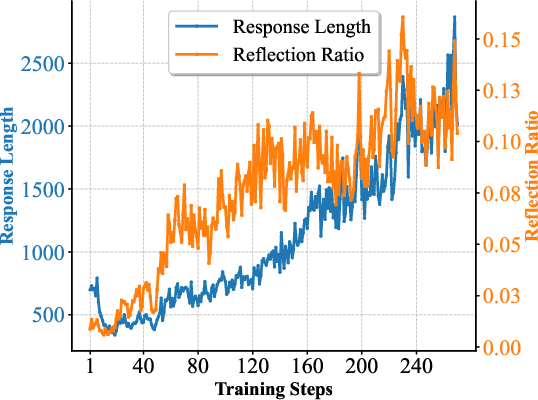
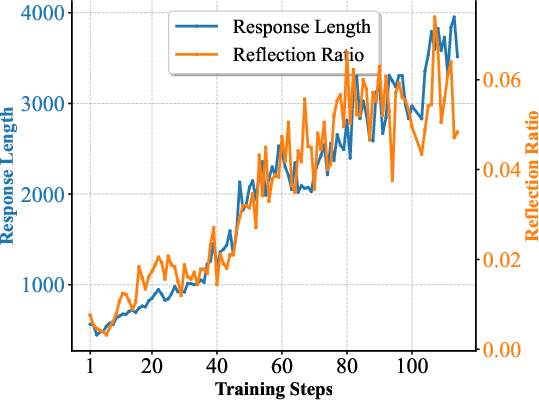
Figure 3: Analysis of response length and reflection ratio during the 7B and 32B training processes.

Mixed Training and Ablation Studies

The paper explores mixing the #1 data with mathematics or coding data for RL training. Conducting mixed training on the Qwen2.5-7B-Base model improves training efficiency for developing mathematical and coding skills. For mathematics, mixed training maintains similar mathematics performance under the same number of training steps, which consumes fewer math training samples. A similar trend is observed when mixing #1 with coding data. The authors conduct large-scale mixed training on the Qwen2.5-32B-Base model to enhance the capability of Zero-RL training. The mixed training achieves superior performance on multiple benchmarks compared to the DeepSeek-R1-Zero-Qwen-32B model.

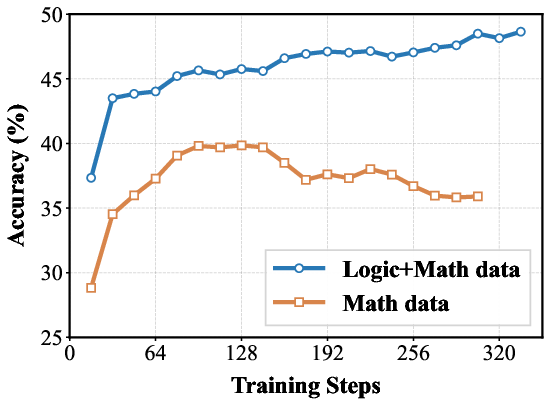
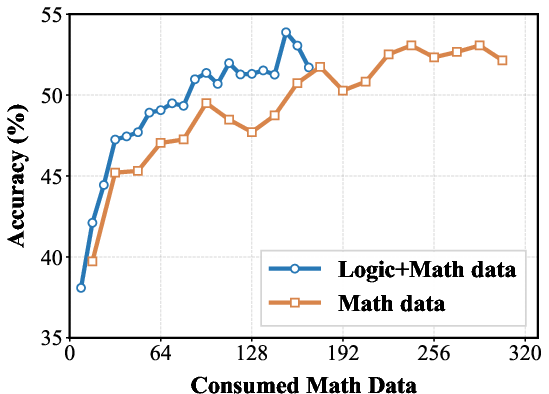
Figure 4: Performance comparison of 7B models trained on mixed data (Logic+Math) versus math-only data.

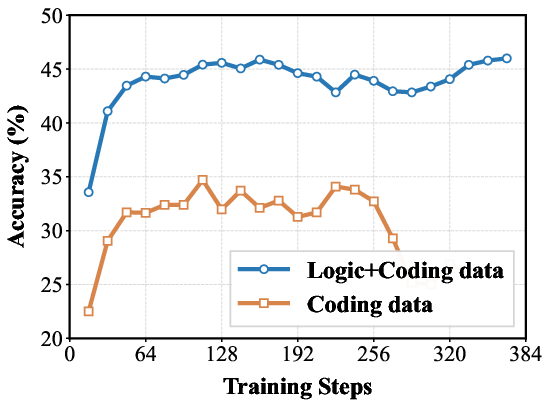
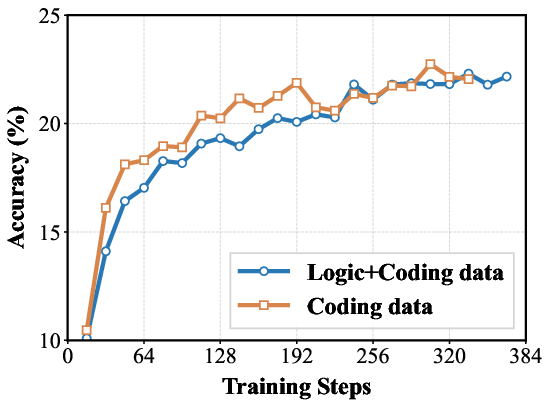
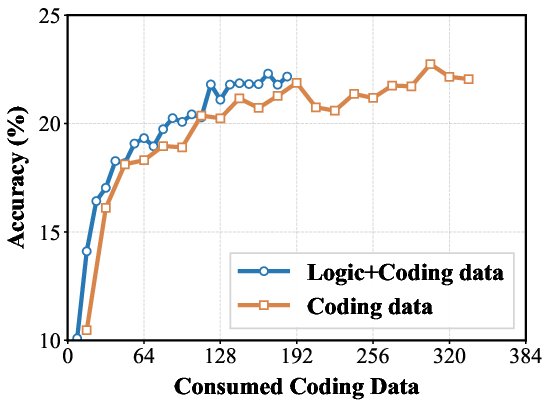
Figure 5: Performance comparison of 7B models trained on mixed data (Logic+Coding) versus coding-only data.

The results strongly validate the generalization benefits provided by the inclusion of #1. (Figure 4) and (Figure 5) presents a comparison of training dynamics. The figures show that models trained on Logic+Coding data achieve higher performance on coding benchmarks than code-only training when consuming the same volume of coding data.

Conclusion

The paper presents #1, a data synthesis framework and dataset for generating diverse logical reasoning data at scale. The framework enables controlled synthesis of data with adjustable difficulty and quantity, with all examples being verifiable by simple rules. RL training on the #1 dataset achieves significant gains on logic benchmarks and strong generalization to unseen mathematical tasks. Mixed training with #1 further improves training efficiency and performance. The authors suggest that #1 inspires broader exploration of synthetic datasets and logical reasoning to develop stronger reasoning capability models.