Scaling up Multi-Turn Off-Policy RL and Multi-Agent Tree Search for LLM Step-Provers (2509.06493v1)

Abstract: The integration of LLMs into automated theorem proving has shown immense promise, yet is fundamentally constrained by challenges in scaling up both training-time reinforcement learning (RL) and inference-time compute. This paper introduces \texttt{BFS-Prover-V2}, a system designed to address this dual scaling problem. We present two primary innovations. The first is a novel multi-turn off-policy RL framework for continually improving the performance of LLM step-prover at training time. This framework, inspired by the principles of AlphaZero, utilizes a multi-stage expert iteration pipeline featuring adaptive tactic-level data filtering and periodic retraining to surmount the performance plateaus that typically curtail long-term RL in LLM-based agents. The second innovation is a planner-enhanced multi-agent search architecture that scales reasoning capabilities at inference time. This architecture employs a general reasoning model as a high-level planner to iteratively decompose complex theorems into a sequence of simpler subgoals. This hierarchical approach substantially reduces the search space, enabling a team of parallel prover agents to collaborate efficiently by leveraging a shared proof cache. We demonstrate that this dual approach to scaling yields state-of-the-art results on established formal mathematics benchmarks. \texttt{BFS-Prover-V2} achieves 95.08\% and 41.4\% on the MiniF2F and ProofNet test sets respectively. While demonstrated in the domain of formal mathematics, the RL and inference techniques presented in this work are of broader interest and may be applied to other domains requiring long-horizon multi-turn reasoning and complex search.

• The paper demonstrates a dual scaling approach by combining multi-turn off-policy RL with planner-enhanced multi-agent tree search to overcome performance plateaus in LLM-based theorem proving.
• It employs adaptive tactic-level perplexity filtering and periodic retraining to focus on challenging proof steps and escape local optima.
• Empirical results on benchmarks like MiniF2F and ProofNet showcase concise, incremental proof generation that enhances computational efficiency.

Scaling Multi-Turn RL and Multi-Agent Tree Search for LLM Step-Provers

Introduction and Motivation

This paper addresses the dual scaling challenges in LLM-based automated theorem proving (ATP): sustaining long-horizon learning during training and efficiently managing combinatorial search at inference. The authors introduce BFS-Prover-V2, a system for Lean4 formal mathematics, which integrates a multi-turn off-policy RL framework with a planner-enhanced multi-agent tree search architecture. The system is designed to overcome performance plateaus in RL and to enable hierarchical, collaborative search for complex theorem proving.

Training-Time Scaling: Multi-Stage Expert Iteration

The training pipeline is formulated as a Markov Decision Process (MDP), where the LLM acts as a policy generating Lean tactics, and the Lean compiler provides deterministic state transitions and reward signals. The core training loop is an expert iteration process, inspired by AlphaZero, alternating between proof generation (via best-first tree search) and model refinement.

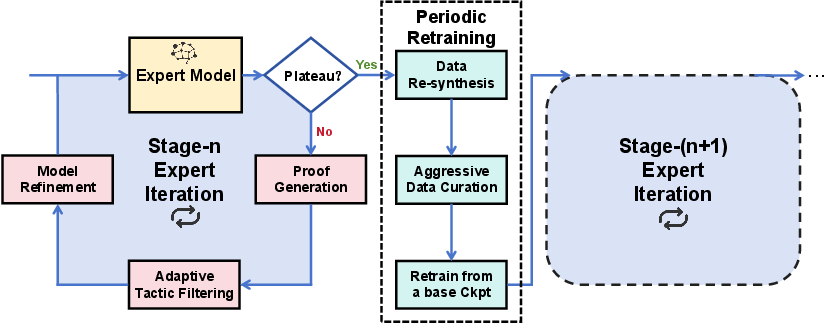
Figure 1: Overview of the training-time scaling up architecture, showing the interplay between expert iteration and periodic retraining to escape plateaus.

Adaptive Tactic-Level Data Filtering

A key innovation is the use of tactic-level perplexity-based filtering. Rather than filtering at the problem level, the system analyzes the distribution of tactic perplexity (negative log-probability) and discards both low-perplexity (trivial) and high-perplexity (noisy or overly complex) tactics. Training is focused on the central region, which represents challenging but learnable steps, thus automating curriculum learning and preventing overfitting.

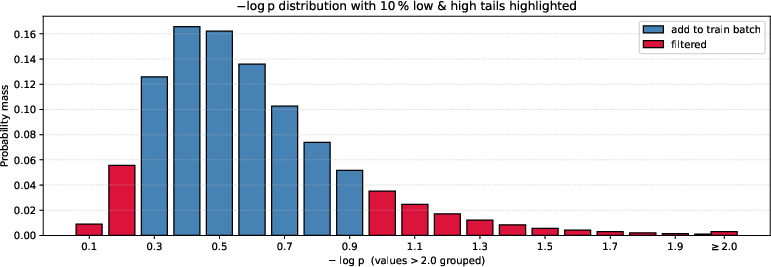
Figure 2: Tactic-Level Data Filtering Based on the Perplexity Distribution, focusing training on the central "goldilocks" zone.

Periodic Retraining ("Soft Reset")

To escape local optima, the system periodically re-solves all previously encountered problems using the current expert, generating cleaner and more concise proofs. Aggressive data curation is then applied, and the model is retrained from a base checkpoint on this refined dataset. This "soft reset" increases the model's entropy and exploratory capacity, enabling it to discover novel proof strategies and achieve monotonic performance improvement.

Figure 3: Sustained Performance Improvement through Expert Iteration and Periodic Retraining, with performance jumps after each retraining phase.

Inference-Time Scaling: Planner-Enhanced Multi-Agent Tree Search

At inference, the system employs a hierarchical planner-prover architecture. A general-purpose reasoning LLM (Planner) decomposes the main theorem into a sequence of subgoals, which are then solved in parallel by multiple Prover agents using best-first tree search. Proven subgoals are added to the proof context, and failures trigger dynamic replanning, allowing the system to adaptively refine its strategy.

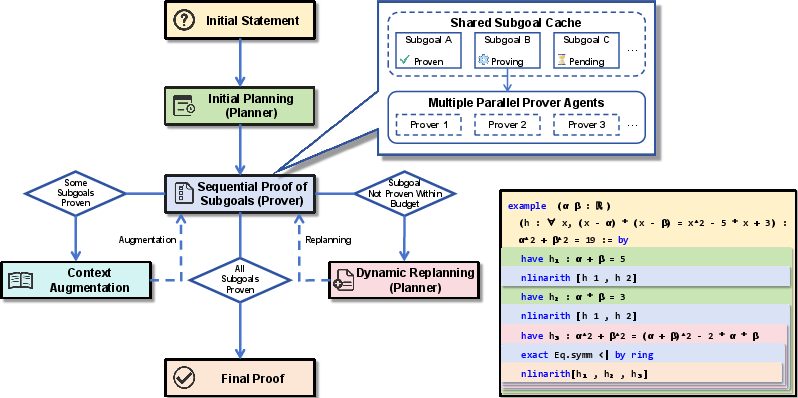
Figure 4: Overview of the planner-enhanced multi-agent tree search architecture, illustrating subgoal decomposition and parallel proving.

Multi-Agent Collaboration and Shared Subgoal Cache

The system implements focused parallelism, where all Prover agents concentrate on a single subgoal at a time, leveraging a shared subgoal cache for coordination. This design maximizes computational efficiency and ensures that resources are not wasted on invalidated subgoals. The cache tracks subgoal status and stores proofs, enabling rapid context augmentation and dynamic replanning.

Implementation Details and Empirical Results

The LLM Prover is based on Qwen2.5-Math-7B/32B, initialized from BFS-Prover-V1. Training data is autoformalized from NuminaMath and Goedel-Prover datasets, totaling ~3M formal statements. Training alternates between continuous fine-tuning and full retraining, with aggressive data curation triggered by performance plateaus.

Inference uses BFS with temperature 1.3, expansion width 3, and length normalization 2.0. The Planner is implemented with Gemini2.5-pro, but other models are compatible given proper prompting.

On MiniF2F (high-school competition math), BFS-Prover-V2 achieves 95.08% (test) and 95.49% (validation). On ProofNet (undergraduate-level library), it achieves 41.4%. These results surpass previous step-provers and are competitive with whole-proof generation models, demonstrating strong generalization and mastery of the problem distribution.

Comparative Analysis: Step-Level vs. Whole-Proof Paradigms

Step-level proof generation yields dramatically shorter and more concise proofs compared to whole-proof models, as shown in the case studies. The interactive approach enables the model to leverage high-level tactics and discover novel strategies, such as direct invocation of library theorems (e.g., AM-GM inequality) and polynomial transformations in trigonometric identities. However, step-level proofs tend to be less readable for humans due to their incremental nature.

Implications and Future Directions

The dual scaling approach—combining adaptive RL with hierarchical, planner-guided search—demonstrates that LLM-based step-provers can achieve state-of-the-art performance in formal mathematics. The system's ability to escape local optima and discover novel strategies suggests that similar architectures could be applied to other domains requiring long-horizon, multi-turn reasoning (e.g., program synthesis, scientific discovery).

Future work may focus on improving the readability of step-level proofs, integrating more advanced planning agents, and extending the framework to richer mathematical libraries and other formal systems. The periodic retraining and adaptive filtering techniques are broadly applicable to RL in LLMs, offering a principled solution to stagnation and mode collapse.

Conclusion

BFS-Prover-V2 presents a comprehensive solution to the dual scaling challenges in LLM-based theorem proving. Its multi-stage expert iteration pipeline and planner-enhanced multi-agent search enable sustained learning and efficient inference, yielding state-of-the-art results on formal mathematics benchmarks. The system's architectural innovations have significant implications for the development of robust, general-purpose reasoning agents in AI.