Elucidating the Design Space of Decay in Linear Attention (2509.05282v1)
Abstract: This paper presents a comprehensive investigation into the decay mechanisms inherent in linear complexity sequence models. We systematically delineate the design space of decay mechanisms across four pivotal dimensions: parameterization strategy, which refers to the computational methodology for decay; parameter sharing, which involves the utilization of supplementary parameters for decay computation; decay granularity, comparing scalar versus vector-based decay; and compatibility with relative positional encoding methods, such as Rotary Position Embedding (RoPE). Through an extensive series of experiments conducted on diverse language modeling tasks, we uncovered several critical insights. Firstly, the design of the parameterization strategy for decay requires meticulous consideration. Our findings indicate that effective configurations are typically confined to a specific range of parameters. Secondly, parameter sharing cannot be used arbitrarily, as it may cause decay values to be too large or too small, thereby significantly impacting performance. Thirdly, under identical parameterization strategies, scalar decay generally underperforms compared to its vector-based counterpart. However, in certain scenarios with alternative parameterization strategies, scalar decay may unexpectedly surpass vector decay in efficacy. Lastly, our analysis reveals that RoPE, a commonly employed relative positional encoding method, typically fails to provide tangible benefits to the majority of linear attention mechanisms.
Summary
- The paper presents a comprehensive evaluation of decay mechanisms by dissecting parameterization strategy, parameter sharing, decay granularity, and positional encoding compatibility.
- Methodology comparisons reveal vector decay often outperforms scalar decay, with Mamba2 demonstrating robust performance across various model sizes.
- A simplified decay parameterization is proposed that matches or exceeds existing methods, offering actionable guidance for optimizing linear attention models.
Elucidating the Design Space of Decay in Linear Attention
The paper "Elucidating the Design Space of Decay in Linear Attention" presents a systematic investigation into the decay mechanisms in linear complexity sequence models. It aims to delineate the architecture of decay mechanisms across several key design dimensions.
Design Dimensions of Decay Mechanisms
The research identifies four primary dimensions for designing decay mechanisms:
- Parameterization Strategy: This involves the computational strategy for computing decay values, whether static, trainable, or input-dependent.
- Parameter Sharing: Investigates whether supplementary parameters are allocated for decay computation separate from other model components.
- Decay Granularity: Distinguishes between scalar decay (uniform across dimensions) and vector decay (dimension-specific coefficients).
- Compatibility with Positional Encoding: Examines how decay mechanisms interact with relative positional encoding techniques like RoPE.
Figure 1: Model architecture diagram of Decay Linear Transformer: Each Decay Linear Transformer consists of multiple Decay Linear Transformer Layers, with each Layer comprising Decay Linear Attention and GLU; for Decay Linear Attention, its computational logic is shown in the right figure.
Parameterization Strategy Analysis
The paper evaluates several parameterization strategies including Mamba2, GLA, Hgrn2, and LightNet, particularly concerning Vector Decay. Mamba2 demonstrated superior performance across all model sizes, owing primarily to its effective handling of decay values, typically centering around a median of 0.8. The ablation studies revealed that the parameter is critical for maintaining this performance.
Figure 2: Distribution of median decay values for each layer across different methods, with model size of 160M. Left figure: Median distribution of Vector Decay. Right figure: Median distribution of Mamba ablation under Vector Decay.
Parameter Sharing Implications
The analysis reveals that parameter sharing can lead to decay values being either too large or too small, adversely affecting model performance. Notably, models like Mamba2 and Hgrn2 appear robust to parameter sharing, whereas GLA and LightNet suffer significant performance degradation due to skewed decay distributions.
Figure 3: Distribution of median decay values for each layer across different methods, with model size of 160M. Left figure: Median distribution of Share Decay. Right figure: Median distribution of Scalar Decay.
Decay Granularity Considerations
The investigation into decay granularity showed that under the same parameterization strategy, vector decay outperforms scalar decay consistently. However, scalar decay can surpass vector decay when paired with different parameterization strategies, especially when the decay values are large, indicating the importance of achieving an optimal range of decay values rather than mere dependence on data.
Positional Encoding Compatibility
The research demonstrates that for linear attention models where decay values are often less than 1, the compatibility with RoPE or TPE does not provide significant performance benefits due to the decay's intrinsic locality bias, mitigating the need for additional positional encoding.
Proposed Simple Decay Parameterization
The paper proposes a simplified decay parameterization called Simple Decay, initialized via , where is the median decay value at initialization. When tested, Simple Decay with matches or exceeds the performance of Mamba2, providing a less complex yet effective parameterization scheme.
Figure 4: Visualization of median decay values for each layer in Simple Decay with different p initializations, for model sizes of 160M and 410M.
Conclusion
This paper maps a comprehensive design space for decay in linear attention, revealing the intricacies and dependencies of different design choices. It provides key insights and actionable guidelines for optimizing decay mechanisms, aiding in the development of efficient linear attention models. Future work could explore the potential of these findings in larger models and diverse application contexts.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper studies a special “memory fade” setting inside fast LLMs called linear attention. Regular Transformers can be slow on long texts because their attention cost grows very fast with length. Linear attention is a family of methods that keep the cost growing only linearly, making them faster. But to work well, these models often need a “decay” or “fade” mechanism that tells the model how much to forget older information.
The authors explore many ways to design this decay and figure out which choices work best.
What questions did the researchers ask?
They looked at four simple questions about how to set the “fade” in linear attention:
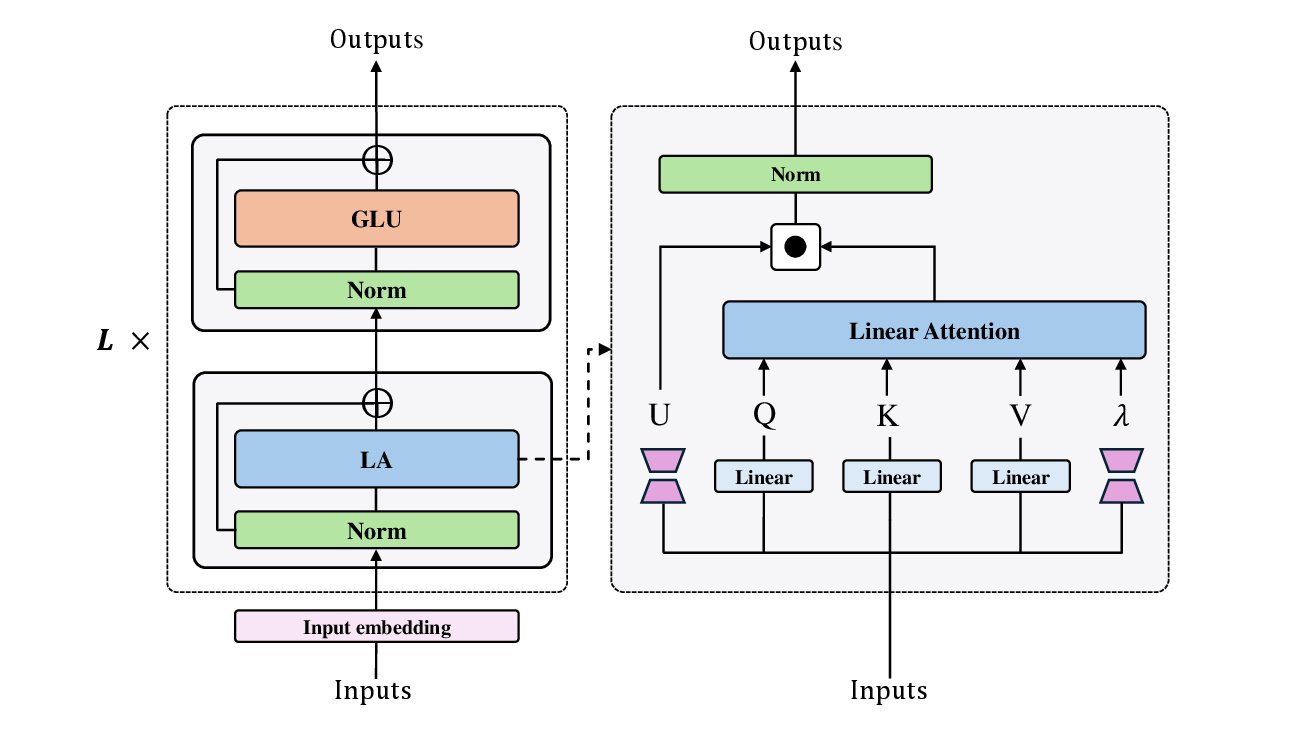
- Parameterization strategy: How do we compute the amount of fading at each step? Is it fixed, learned, or based on the input?
- Parameter sharing: Should the numbers used for computing “fade” also be reused for other parts (like keys), or should “fade” have its own separate parameters?
- Decay granularity: Should there be one fade value per head (scalar decay), or a separate fade value for every feature/channel (vector decay)?
- Positional encoding: Do extra tricks for ordering words in a sentence (like RoPE) still help when we already have decay?
How did they paper it?
They built a standard testbed model so that all experiments are fair and comparable. Then they:
- Trained LLMs of different sizes (about 160M, 410M, and 1.45B parameters) on a large text dataset.
- Tested several known decay designs from recent models (like Mamba2, GLA, HGRN2, LightNet, and TNL), plus some new variations.
- Measured how well models predict text (perplexity) and how well they do on question-answering and reasoning tasks (accuracy).
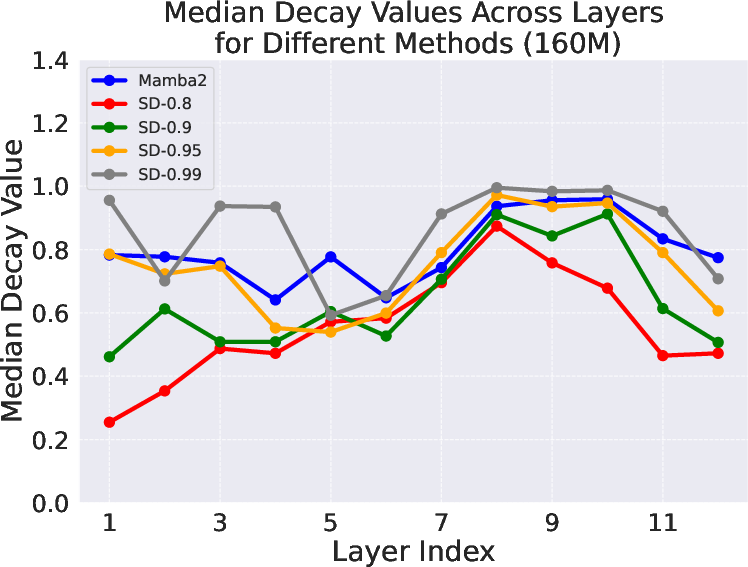
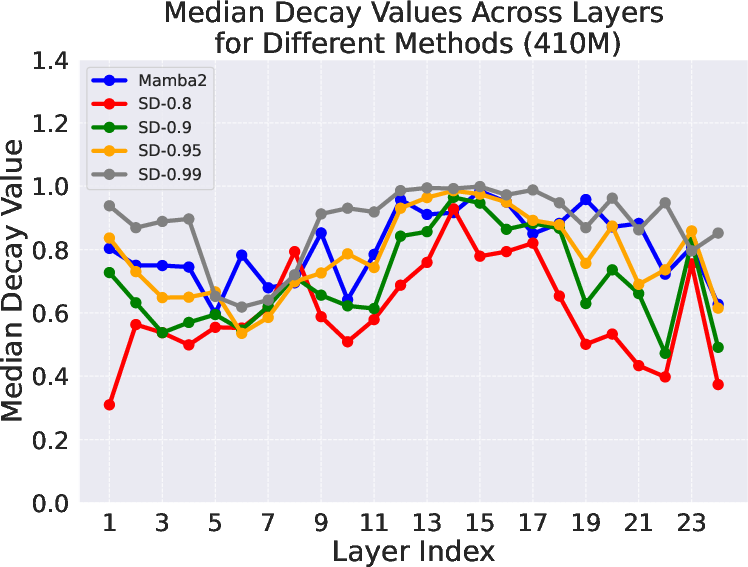
- Looked at the actual fade values learned by the models to see patterns—especially the “median decay,” which tells you the typical strength of fading across layers.
Think of it like tuning a set of dimmer switches (decay values) that control how quickly earlier words fade into the background. The team tried different rules for setting these dimmers and checked which rules lead to better reading and reasoning.
Key terms explained in everyday language
- Linear attention: A way for the model to handle long texts efficiently by simplifying how attention is computed.
- Decay (fade): A knob that controls how strongly older information is remembered. Near 1 means “remember a lot,” near 0 means “forget quickly.”
- Scalar decay vs. vector decay:
- Scalar: One knob per head (coarse control).
- Vector: Many knobs per head, one for each feature (fine-grained control).
- Parameter sharing: Using the same learned numbers for both the fade and other parts of attention, instead of giving the fade its own separate numbers.
- Positional encoding (like RoPE, TPE): Extra information that helps the model understand the order of words.
What did they find?
Here are the main takeaways from their experiments:
- The “how to compute fade” choice matters a lot.
- A popular strategy from Mamba2 worked best overall.
- A version of Mamba2 without one of its pieces (called A) often worked just as well, but removing another piece (Δ) hurt performance.
- Good models typically had median fade values around 0.8. If fade is too small (near 0), the model forgets too fast. If it’s too big (near 1), the model barely forgets and gets “attention dilution” (too much old info crowds out what matters now).
- Be careful with parameter sharing.
- Reusing the same parameters for computing both fade and other parts can push fade values too high or too low and hurt performance in several methods.
- For some designs (like Mamba2 and HGRN2), sharing didn’t change much; for others (like GLA and LightNet), it made things worse.
- Vector decay usually beats scalar decay when everything else is the same.
- Having one fade knob per feature (vector) gives finer control and typically performs better than a single knob (scalar).
- However, a well-chosen scalar strategy can beat a poorly chosen vector strategy. The formula and the typical range of fade values matter more than scalar vs. vector alone.
- Positional encodings like RoPE often don’t help these linear attention models much.
- Because decay already makes the model focus more on nearby words (a built-in “locality” effect), adding RoPE/TPE usually brings little or no benefit.
- A simple new decay recipe works well.
- The authors propose “Simple Decay,” a clean formula that mainly sets a target starting value for the fade and lets the model adjust from there.
- With high initial settings (like starting near 0.95 or 0.99), this simple method matched or beat the strong Mamba2 approach in their tests.
- Results also hold in a more expressive setup (DPLR).
- Even when the state update is more complex (diagonal plus low-rank), having decay helps a lot; vector decay > scalar decay > no decay.
Why does it matter?
This work gives practical, easy-to-follow rules for building faster LLMs that still perform well:
- Choose a decay formula that keeps typical fade around 0.8 after training.
- Avoid making fade too close to 0 or 1 across layers.
- Prefer vector decay when possible, but remember that the exact formula and fade range matter most.
- Be cautious with parameter sharing; it can accidentally break the fade behavior.
- Don’t expect big gains from adding RoPE/TPE when your decay already focuses attention locally.
- A simple decay setup with a good starting value can perform excellently and be easier to implement.
Overall, these insights can help researchers and engineers design efficient models that handle long texts well, train faster, and still get strong results—useful for building the next generation of practical, scalable AI systems.
Knowledge Gaps
Below is a single, actionable list of knowledge gaps, limitations, and open questions that remain unresolved by the paper.
- External validity of the “optimal decay median ≈ 0.8”: The claim is empirical and tied to specific architectures (silu kernel, TNL-style gating, RMSNorm), model sizes (160M–1.45B), dataset (fineweb-edu-10B), and training recipe. It is unknown whether this target holds for larger scales (≥7B), different kernels (e.g., cosine, exp, elu+1), other normalizations, deeper networks, or different optimizers/schedules.
- Limited task coverage and context regimes: Evaluations are confined to perplexity and a small set of zero-shot tasks with 2k context. The impact of decay design on long-context generalization (≥32k), long-range benchmarks (e.g., PG-19, LRA), retrieval tasks, code generation, reasoning (math/logic), and multilingual settings is untested.
- Statistical robustness and variance: Results lack multiple seeds, standard deviations, and statistical tests. It’s unclear how sensitive conclusions are to initialization noise, token budget, and training instabilities.
- Fairness of parameter-sharing conclusion: “Parameter sharing” is implemented as k = 1 − λ, which is a strong and specific coupling. It remains unknown whether other sharing schemes (e.g., shared projections, partial coupling, auxiliary gates) yield different outcomes, especially for methods like HGRN2 that share parameters more subtly.
- Vector decay incompatibility with RoPE: The paper excludes vector decay + RoPE due to naive incompatibility. It remains open whether modified or decomposable rotations (e.g., per-dimension rotations that commute with diag(λ), block-structured rotations, or learned phase/scale) could enable effective vector-decay–RPE integration.
- Lack of theoretical grounding: There is no theoretical explanation for why certain decay ranges perform best, how decay interacts with kernelized attention or state-space dynamics, or the conditions under which decay aids stability, memory retention, and expressivity.
- Sensitivity to training recipe: Only one optimizer (AdamW), scheduler (WSD), and LR are used. The dependence of decay distributions and performance on LR schedules, weight decay, gradient clipping, dropout, warmup, or data order is unknown.
- Kernel and architecture dependence: The paper fixes silu as the attention kernel and adopts specific gating and normalization. How decay interacts with other kernels (cosine, Performer, FAVOR+), gating variants, normalization choices (LayerNorm, ScaleNorm), and feed-forward designs is not explored.
- Computational efficiency and memory trade-offs: There are no runtime, memory, or throughput measurements for scalar vs vector decay, different parameterizations, or RPE/TPE integrations. The practical costs at training and inference time remain unclear.
- Generalization across data domains: Results rely on fineweb-edu-10B. It is unknown whether conclusions transfer to code-heavy corpora, scientific/math text, speech, or multimodal pretraining.
- Decay dynamics over training: The paper reports post-hoc medians but does not analyze the temporal evolution of decay distributions, layer/head-specific trends, or their relationship to optimization dynamics, gradient flow, and convergence speed.
- Decay near-boundary behavior: Numerical stability and training behavior when λ approaches 1 (or 0) are not analyzed (e.g., state explosion/vanishing, need for clipping, bias correction, or re-normalization).
- DPLR interactions: The DPLR extension is limited and does not probe how decay should couple with low-rank dynamics (e.g., tying decay to low-rank modes, rank selection, stability constraints), or whether decay should be applied differently to diagonal vs low-rank components.
- Role of data dependence vs value range: The paper observes that the range of λ can trump data dependence, but does not formalize when data-conditional decay is useful, nor characterize tasks where conditional decay yields gains beyond setting a good λ range.
- Simple Decay initialization p: Only a few global p values (0.8–0.99) are tested. Open questions include per-layer/per-head p initialization, learned p schedules (annealing), p priors tied to depth/width, and robustness of Simple Decay across recipes and datasets.
- Positional encoding alternatives: LRPE is excluded due to doubling head dimension; other decomposable RPEs, hybrid schemes (absolute+relative), or lightweight RoPE variants compatible with vector decay remain unexplored.
- Context-length extrapolation: Models are trained/evaluated at 2k tokens. The behavior of decay distributions and performance when extrapolating to much longer inference contexts (8k–128k) is untested.
- Confounds in scalar vs vector comparisons: It is not fully verified that parameter counts and capacity are strictly matched across scalar/vector settings and parameterizations, leaving open whether some gains are due to capacity differences rather than granularity per se.
- Fidelity to original baselines: Some implementations (e.g., Mamba2 without A, HGRN2’s shared decay) deviate from canonical architectures. It remains unclear how closely conclusions carry over to official implementations and training pipelines.
- Interpretability of decay: There is no analysis of what dimensions/heads with specific decay values represent, how decay aligns with linguistic structure or features, or whether decay patterns correlate with attention sparsity, locality, or syntactic/semantic roles.
- Robustness and distribution shift: The influence of decay design on robustness to noise, domain shift, adversarial prompts, and calibration is not examined.
- Fine-tuning and downstream adaptation: Effects of decay choices on instruction tuning, RLHF, or task-specific fine-tuning (e.g., SFT/PEFT) are unknown.
- Combined design knobs: Interactions among the four dimensions (parameterization, sharing, granularity, positional encoding) are largely studied in isolation; systematic joint optimization or automated search across the design space remains an open direction.
Collections
Sign up for free to add this paper to one or more collections.