An overview of Koopman-based control: From error bounds to closed-loop guarantees (2509.02839v1)

Abstract: Controlling nonlinear dynamical systems remains a central challenge in a wide range of applications, particularly when accurate first-principle models are unavailable. Data-driven approaches offer a promising alternative by designing controllers directly from observed trajectories. A wide range of data-driven methods relies on the Koopman-operator framework that enables linear representations of nonlinear dynamics via lifting into higher-dimensional observable spaces. Finite-dimensional approximations, such as extended dynamic mode decomposition (EDMD) and its controlled variants, make prediction and feedback control tractable but introduce approximation errors that must be accounted for to provide rigorous closed-loop guarantees. This survey provides a systematic overview of Koopman-based control, emphasizing the connection between data-driven surrogate models generated from finite data, approximation errors, controller design, and closed-loop guarantees. We review theoretical foundations, error bounds, and both linear and bilinear EDMD-based control schemes, highlighting robust strategies that ensure stability and performance. Finally, we discuss open challenges and future directions at the interface of operator theory, approximation theory, and nonlinear control.

• The paper demonstrates a Koopman-based control framework that establishes finite-data error bounds and closed-loop guarantees for nonlinear systems.
• It details the extension from linear to bilinear surrogate models, providing rigorous error analysis with proportional bounds for robust controller synthesis.
• The research emphasizes practical considerations including data requirements, dictionary selection, and computational complexity for real-world deployment.

Koopman-Based Control: Error Bounds and Closed-Loop Guarantees

Introduction

This paper provides a comprehensive survey of Koopman-based control, focusing on the interplay between data-driven surrogate modeling, finite-data error bounds, controller synthesis, and closed-loop guarantees for nonlinear dynamical systems. The Koopman operator framework enables the linearization of nonlinear dynamics by lifting them into higher-dimensional spaces of observables, facilitating the application of linear systems theory to inherently nonlinear problems. The survey systematically reviews theoretical foundations, error analysis, and practical control schemes, emphasizing rigorous guarantees and highlighting open challenges in the field.

Koopman Operator Theory and Data-Driven Approximation

The Koopman operator $\mathcal{K}$ acts on observables $\psi$ of the state space, propagating them linearly in an infinite-dimensional function space. For a nonlinear system $\dot{x} = f(x)$, the operator satisfies $(\mathcal{K}^t \psi)(\hat{x}) = \psi(x(t;\hat{x}))$, trading nonlinearity for infinite dimensionality. The generator $\mathcal{L}$ provides a differential counterpart, with $$(\mathcal{L} \psi)(x) = \langle \nabla \psi(x), f(x) \rangle$$.

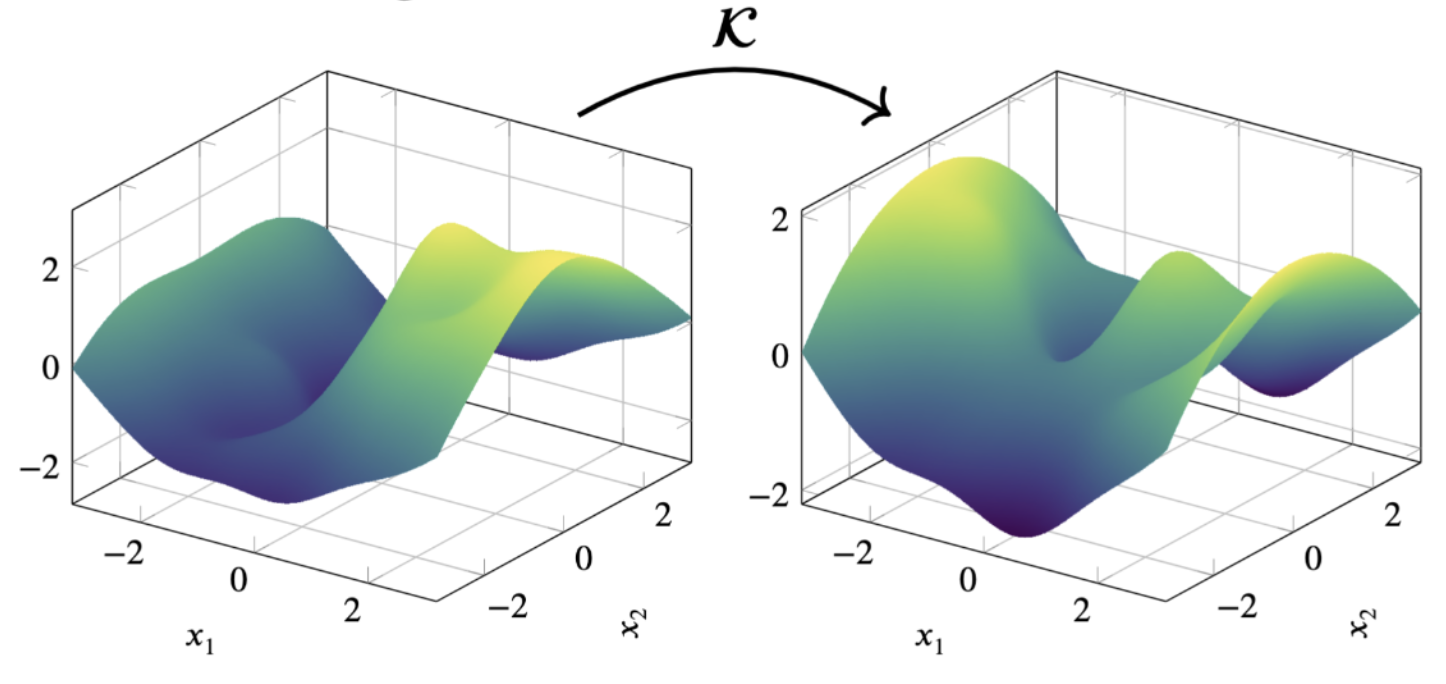
Figure 1: Illustration of the action of the Koopman operator $\mathcal{K}$, mapping observables along system trajectories.

Finite-dimensional approximations are constructed via Extended Dynamic Mode Decomposition (EDMD), which solves a regression problem over a chosen dictionary of observables. The accuracy of EDMD depends on both the richness of the dictionary and the amount of data, with convergence to the true operator in the infinite-data and infinite-dictionary limit. Recent advances provide probabilistic and deterministic error bounds for finite data, including pointwise ($L^\infty$) bounds via kernel-based EDMD (kEDMD), leveraging RKHS theory and fill distance metrics.

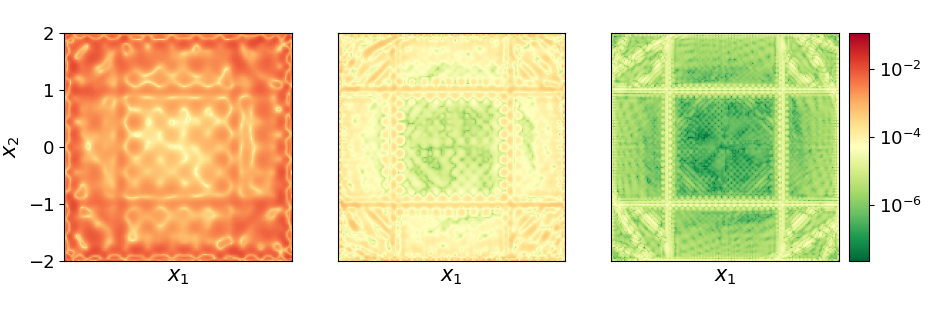
Figure 2: Approximation error for decreasing fill distance $h_\mathcal{X}$, demonstrating improved accuracy with denser sampling.

Koopman-Based Control: Linear and Bilinear Surrogates

Linear EDMD with Control (EDMDc)

EDMDc extends EDMD to controlled systems, learning a linear surrogate model in the lifted space:

$\Psi(x^+) \approx A \Psi(x) + B u$

where $A$ and $B$ are estimated via least-squares regression. While this enables the use of linear control techniques (e.g., LQR, MPC), it is fundamentally limited: the true Koopman operator for controlled systems is generally not linear in the lifted state unless the dictionary is carefully chosen and the system is control-affine. This leads to intrinsic approximation errors and a lack of closed-loop guarantees.

Bilinear EDMD with Control

To address these limitations, bilinear surrogate models are introduced:

$$\Psi(x^+) \approx A \Psi(x) + B_0 u + \sum_{i=1}^m u_i B_i \Psi(x)$$

This structure more accurately captures the interaction between state and input, and is amenable to rigorous error analysis. SafEDMD and kernel-based EDMDc provide proportional error bounds on the residual, of the form:

$\|r(x,u)\|_2 \leq c_x \|\Psi(x)\|_2 + c_u \|u\|_2$

where $c_x, c_u$ depend on data size, dictionary richness, and sampling properties. These bounds are crucial for robust controller synthesis.

Controller Synthesis with Closed-Loop Guarantees

Robust Feedback Design

Controllers are synthesized for the uncertain bilinear surrogate, explicitly accounting for the residual error. LMI-based and SOS-based approaches are employed to design nonlinear feedback laws that guarantee exponential stability within a region of attraction characterized by a Lyapunov sublevel set. The SOS approach, in particular, allows for rational dependence on the lifted state and can handle larger regions of attraction and error margins.

Model Predictive Control (MPC)

Koopman-based MPC leverages the bilinear surrogate for prediction and optimization. Practical and asymptotic stability guarantees are established under proportional error bounds and Lipschitz continuity. Kernel-based surrogates facilitate the construction of low-dimensional nonlinear predictors with explicit error characterization, enabling robust MPC for nonlinear systems.

Implementation Considerations

• Data Requirements: Error bounds are conservative; large datasets and dense sampling are often required for rigorous guarantees, though practical performance may be achieved with less data.
• Dictionary Selection: The choice of observables is critical for expressivity and invariance. Automated dictionary learning (e.g., via neural networks) is promising but lacks theoretical guarantees.
• Computational Complexity: Kernel-based methods scale with data size; SOS programs scale rapidly with polynomial degree and system dimension, limiting applicability to high-dimensional systems.
• Deployment: Controllers synthesized in the lifted space must be mapped back to the original state space, often requiring reprojection or delay embedding techniques.

Implications and Future Directions

The survey highlights several open challenges:

• Extending closed-loop guarantees to input-output data settings, where full state measurements are unavailable.
• Reducing conservatism in finite-data error bounds to improve data efficiency.
• Developing principled dictionary learning methods that preserve control-relevant features.
• Enhancing scalability and robustness to noise for high-dimensional and distributed systems.

Addressing these challenges is essential for transitioning Koopman-based control from a theoretical framework to a practical methodology for complex, safety-critical nonlinear systems.

Conclusion

Koopman-based control offers a principled approach to data-driven modeling and control of nonlinear systems, leveraging operator-theoretic lifting and rigorous error analysis. Bilinear surrogate models with proportional error bounds enable robust controller synthesis with closed-loop guarantees. Future research should focus on input-output learning, scalable controller design, and reducing conservatism in error characterization to facilitate real-world adoption in high-dimensional and uncertain environments.